第八章二元一次方程组单元同步检测试题(含答案)2023---2024学年人教版七年级数学下册
文档属性
| 名称 | 第八章二元一次方程组单元同步检测试题(含答案)2023---2024学年人教版七年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 245.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 15:56:23 | ||
图片预览



文档简介
第八章《二元一次方程组》单元检测题
一、选择题(每题3分,共30分)
1.若是二元一次方程,那么、的值分别为( )
A., B., C., D.,
2.已知 是二元一次方程组的解,则m-的值是( )
A.1 B.-2 C.3 D.-4
3.用加减消元法解二元一次方程组时,下列方法中无法消元的是( )
A.①×2﹣② B.②×(﹣3)﹣① C.①×(﹣2)+② D.①﹣②×3
4.二元一次方程3x+y=8的正整数解有( )
A.2个 B.3个 C.4个 D.5个
5.已知是二元一次方程组的解,则代数式的值为( )
A. B. C. D.
6.如果,则、的值分别是( )
A. B. C. D.
7.若和是方程的两组解,则m,n的值分别为( )
A., B.2,4 C.4,2 D.,
8.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.2023年成都大运会上,努力拼搏的不只有运动员们,在赛场外,到处都能看到志者们忙碌的身影,大批大学生报名参与志愿者服务工作,某大学计划组织本校学生志愿者乘车去了解比赛场馆情况,若单独调配30座(不含司机)客车若干辆,则有5人没有座位;若只调配25座(不含司机)客车,则用车数量将增加3辆,并空出5个座位.设计划调配30座客车x辆,该大学共有y名大学生志愿者,则下列方程组正确的是( )
A. B.
C. D.
10.已知关于x,y的方程组给出下列结论:
①当a=3时,方程组的解也是x+y=2a+1的解:
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=9,则a=1.其中正确的有( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题(每题3分,共24分)
11.二元一次方程的正整数解有 组.
12.如果实数满足方程组,则 .
13.若,则的值为 .
14.已知方程组的解为,则的值为__________.
15.已知是方程3mx﹣y=﹣1的解,则m=_____.
16.若关于的二元一次方程组的解是互为相反数,则的值是_________.
17.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为11a厘米,此时木桶中水的深度是 厘米(用含a的代数式表示).
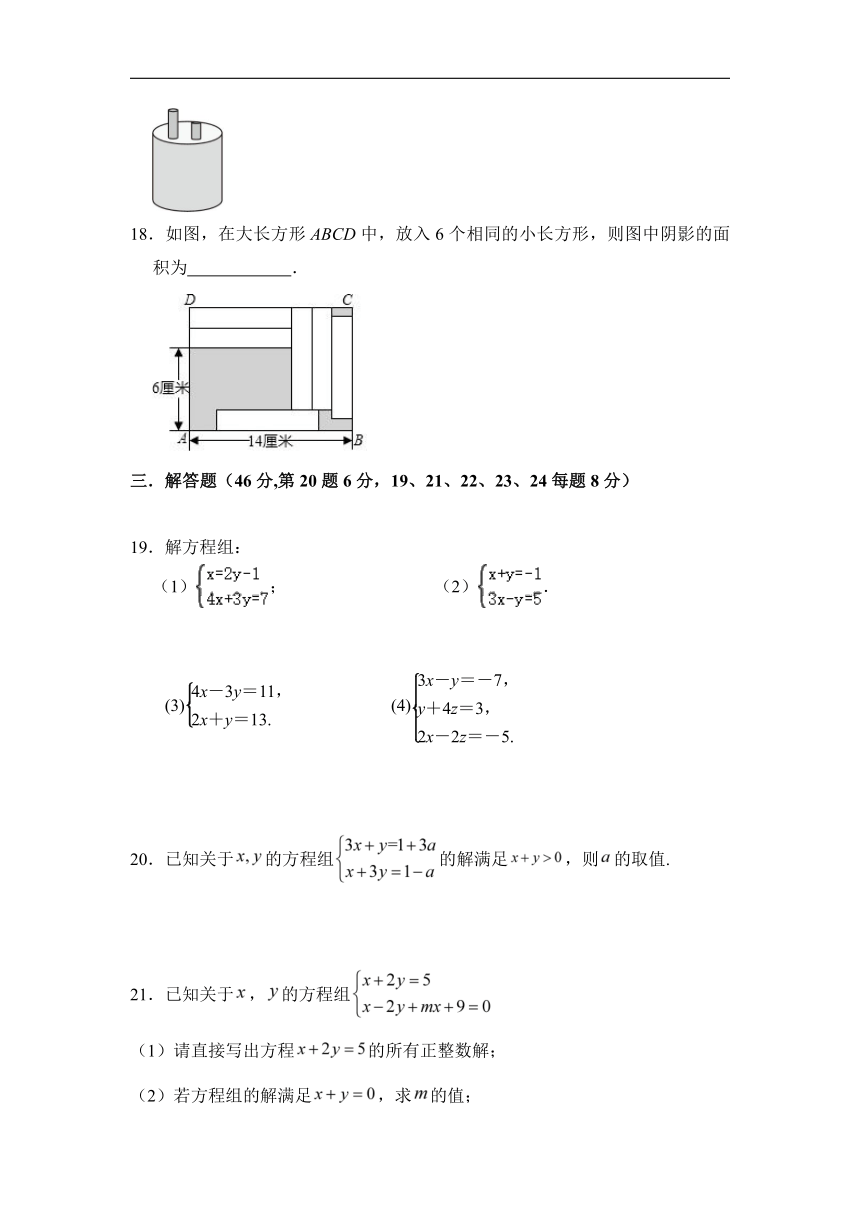
18.如图,在大长方形ABCD中,放入6个相同的小长方形,则图中阴影的面积为 .
三.解答题(46分,第20题6分,19、21、22、23、24每题8分)
19.解方程组:
(1); (2).
(3) (4)
20.已知关于的方程组的解满足,则的取值.
21.已知关于,的方程组
(1)请直接写出方程的所有正整数解;
(2)若方程组的解满足,求的值;
(3)无论实数取何值,方程总有一个公共解,请直接写出这个公共解.
22.如图,在长为10米,宽为8米的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.
23.某工厂现有甲种原料10吨,乙种原料15吨,计划用这两种原料生产、两种产品,两种原料都恰好全部用完.生产一件、一件产品与所需原料情况如下表所示:
甲种原料(吨) 乙种原料(吨)
产品(件) 1 3
产品(件) 2 1
(1)求该厂生产、两种产品各有多少件;
(2)如果购买这批原料共花费5万元,、产品的销售单价分别为2万元/件和3万元/件,求全部销售这批产品获得的利润是多少万元.
24.为加快“秀美荆河水系生态治理工程”进度,污水处理厂决定购买10台污水处理设备.现有A,B两种型号的设备,每台的价格分别为a万元,b万元,每月处理污水量分别为240吨,200吨.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值;
(2)厂里预算购买污水处理设备的资金不超过105万元,你认为有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为污水处理厂设计一种最省钱的购买方案.
【答案】
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D A D B C B A C
二、填空题:
11.解:二元一次方程的正整数解有,,共2组,
故答案为:2.
12.解:∵,
,得:,
∴;
故答案为:2023.
13.解:∵,
∴,
∴,
∴,得,
故答案为:4.
14.6
15.
16.9
17. .
18..
三.解答题
19.解:(1)
,
把①代入②得:4(2y﹣1)+3y=7,
解得:y=1,
把y=1代入①得:x=1,
则方程组的解为;
(2)
,
①+②得:4x=4,
解得:x=1,
把x=1代入①得:y=﹣2,
则方程组的解为.
(3)
①+②×3,得10x=50,
解得x=5.
把x=5代入②,
得2×5+y=13,解得y=3.
于是,得方程组的解为
(4)
①+②得3x+4z=-4.④
④+③×2得x=-2.
把x=-2代入①得y=1.
把x=-2代入③得z=.
所以
20.a> 1
21.(1);(2);(3).
22. 8
【解析】
设小长方形的长为 x 米,宽为y米. 依题意有:解方程组即可.
解: 设小长方形的长为 x 米,宽为y米.
依题意有:
解此方程组得:
故,小长方形的长为 4米,宽为2米.
23.(1)种产品4件,种产品3件;(2)利润是12万元.
【分析】
(1)设、两种产品各有件和件,根据题意列二元一次方程组,利用加减法解方程组即可解题;
(2)根据利润=售价-进价解题即可.
【详解】
解:(1)设、两种产品各有件和件,
根据题意得,,
①②得,
,
把代入①,得
,
经检验,符合题意,
答:该厂生产A种产品4件,种产品3件.
(2)万元,
答:全部销售这批产品获得的利润是12万元.
【点睛】
本题考查二元一次方程组的实际应用,是重要考点,难度较易,掌握相关知识是解题关键.
24.(1)a的值为12,b的值为10;(2)有3种购买方案,方案1:购买B型设备10台;方案2:购买A型设备1台,B型设备9台;方案3:购买A型设备2台,B型设备8台;(3)为了节约资金,该公司最省钱的一种购买方案为:购买A型设备1台,B型设备9台.
【分析】
(1)由“已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元”,即可得出关于a、b的二元一次方程组,解之即可得出结论;
(2)设购买A型设备m台,则购买B型设备(10﹣m)台,根据总价=单价×数量结合厂里预算购买污水处理设备的资金不超过105万元,即可得出关于m的一元一次不等式,解之取其中的整数即可得出各购买方案;
(3)由每月要求处理污水量不低于2040吨,来验证m的值,再利用总价=单价×数量找出最省钱的购买方案.
【详解】
解:(1)根据题意得: ,
解得:.
答:a的值为12,b的值为10.
(2)设购买A型设备m台,则购买B型设备(10﹣m)台,
根据题意得:12m+10(10﹣m)≤105,
解得:m≤ ,
∴m可取的值为0,1,2.
故有3种购买方案,方案1:购买B型设备10台;方案2:购买A型设备1台,B型设备9台;方案3:购买A型设备2台,B型设备8台.
(3)当m=0时,每月的污水处理量为:200×10=2000(吨),
∵2000<2040,
∴m=0不合题意,舍去;
当m=1时,每月的污水处理量为:240+200×9=2040(吨),
∵2040=2040,
∴m=1符合题意,此时购买设备所需资金为:12+10×9=102(万元);
当m=2时,每月的污水处理量为:240×2+200×8=2080(吨),
∵2080>2040,
∴m=2符合题意,此时购买设备所需资金为:12×2+10×8=104(万元).
∵102<104,
∴为了节约资金,该公司最省钱的一种购买方案为:购买A型设备1台,B型设备9台.
【点睛】
考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式;(3)由每月要求处理污水量来确定m可取的值.
一、选择题(每题3分,共30分)
1.若是二元一次方程,那么、的值分别为( )
A., B., C., D.,
2.已知 是二元一次方程组的解,则m-的值是( )
A.1 B.-2 C.3 D.-4
3.用加减消元法解二元一次方程组时,下列方法中无法消元的是( )
A.①×2﹣② B.②×(﹣3)﹣① C.①×(﹣2)+② D.①﹣②×3
4.二元一次方程3x+y=8的正整数解有( )
A.2个 B.3个 C.4个 D.5个
5.已知是二元一次方程组的解,则代数式的值为( )
A. B. C. D.
6.如果,则、的值分别是( )
A. B. C. D.
7.若和是方程的两组解,则m,n的值分别为( )
A., B.2,4 C.4,2 D.,
8.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9.2023年成都大运会上,努力拼搏的不只有运动员们,在赛场外,到处都能看到志者们忙碌的身影,大批大学生报名参与志愿者服务工作,某大学计划组织本校学生志愿者乘车去了解比赛场馆情况,若单独调配30座(不含司机)客车若干辆,则有5人没有座位;若只调配25座(不含司机)客车,则用车数量将增加3辆,并空出5个座位.设计划调配30座客车x辆,该大学共有y名大学生志愿者,则下列方程组正确的是( )
A. B.
C. D.
10.已知关于x,y的方程组给出下列结论:
①当a=3时,方程组的解也是x+y=2a+1的解:
②无论a取何值,x,y的值不可能是互为相反数;
③x,y都为自然数的解有4对;
④若2x+y=9,则a=1.其中正确的有( )
A.①②③ B.②③④ C.①③④ D.①②④
二、填空题(每题3分,共24分)
11.二元一次方程的正整数解有 组.
12.如果实数满足方程组,则 .
13.若,则的值为 .
14.已知方程组的解为,则的值为__________.
15.已知是方程3mx﹣y=﹣1的解,则m=_____.
16.若关于的二元一次方程组的解是互为相反数,则的值是_________.
17.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的,两根铁棒长度之和为11a厘米,此时木桶中水的深度是 厘米(用含a的代数式表示).
18.如图,在大长方形ABCD中,放入6个相同的小长方形,则图中阴影的面积为 .
三.解答题(46分,第20题6分,19、21、22、23、24每题8分)
19.解方程组:
(1); (2).
(3) (4)
20.已知关于的方程组的解满足,则的取值.
21.已知关于,的方程组
(1)请直接写出方程的所有正整数解;
(2)若方程组的解满足,求的值;
(3)无论实数取何值,方程总有一个公共解,请直接写出这个公共解.
22.如图,在长为10米,宽为8米的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.
23.某工厂现有甲种原料10吨,乙种原料15吨,计划用这两种原料生产、两种产品,两种原料都恰好全部用完.生产一件、一件产品与所需原料情况如下表所示:
甲种原料(吨) 乙种原料(吨)
产品(件) 1 3
产品(件) 2 1
(1)求该厂生产、两种产品各有多少件;
(2)如果购买这批原料共花费5万元,、产品的销售单价分别为2万元/件和3万元/件,求全部销售这批产品获得的利润是多少万元.
24.为加快“秀美荆河水系生态治理工程”进度,污水处理厂决定购买10台污水处理设备.现有A,B两种型号的设备,每台的价格分别为a万元,b万元,每月处理污水量分别为240吨,200吨.已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元.
(1)求a,b的值;
(2)厂里预算购买污水处理设备的资金不超过105万元,你认为有哪几种购买方案;
(3)在(2)的条件下,若每月要求处理污水量不低于2040吨,为了节约资金,请你为污水处理厂设计一种最省钱的购买方案.
【答案】
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D A D B C B A C
二、填空题:
11.解:二元一次方程的正整数解有,,共2组,
故答案为:2.
12.解:∵,
,得:,
∴;
故答案为:2023.
13.解:∵,
∴,
∴,
∴,得,
故答案为:4.
14.6
15.
16.9
17. .
18..
三.解答题
19.解:(1)
,
把①代入②得:4(2y﹣1)+3y=7,
解得:y=1,
把y=1代入①得:x=1,
则方程组的解为;
(2)
,
①+②得:4x=4,
解得:x=1,
把x=1代入①得:y=﹣2,
则方程组的解为.
(3)
①+②×3,得10x=50,
解得x=5.
把x=5代入②,
得2×5+y=13,解得y=3.
于是,得方程组的解为
(4)
①+②得3x+4z=-4.④
④+③×2得x=-2.
把x=-2代入①得y=1.
把x=-2代入③得z=.
所以
20.a> 1
21.(1);(2);(3).
22. 8
【解析】
设小长方形的长为 x 米,宽为y米. 依题意有:解方程组即可.
解: 设小长方形的长为 x 米,宽为y米.
依题意有:
解此方程组得:
故,小长方形的长为 4米,宽为2米.
23.(1)种产品4件,种产品3件;(2)利润是12万元.
【分析】
(1)设、两种产品各有件和件,根据题意列二元一次方程组,利用加减法解方程组即可解题;
(2)根据利润=售价-进价解题即可.
【详解】
解:(1)设、两种产品各有件和件,
根据题意得,,
①②得,
,
把代入①,得
,
经检验,符合题意,
答:该厂生产A种产品4件,种产品3件.
(2)万元,
答:全部销售这批产品获得的利润是12万元.
【点睛】
本题考查二元一次方程组的实际应用,是重要考点,难度较易,掌握相关知识是解题关键.
24.(1)a的值为12,b的值为10;(2)有3种购买方案,方案1:购买B型设备10台;方案2:购买A型设备1台,B型设备9台;方案3:购买A型设备2台,B型设备8台;(3)为了节约资金,该公司最省钱的一种购买方案为:购买A型设备1台,B型设备9台.
【分析】
(1)由“已知购买一台A型设备比购买一台B型设备多2万元,购买2台A型设备比购买3台B型设备少6万元”,即可得出关于a、b的二元一次方程组,解之即可得出结论;
(2)设购买A型设备m台,则购买B型设备(10﹣m)台,根据总价=单价×数量结合厂里预算购买污水处理设备的资金不超过105万元,即可得出关于m的一元一次不等式,解之取其中的整数即可得出各购买方案;
(3)由每月要求处理污水量不低于2040吨,来验证m的值,再利用总价=单价×数量找出最省钱的购买方案.
【详解】
解:(1)根据题意得: ,
解得:.
答:a的值为12,b的值为10.
(2)设购买A型设备m台,则购买B型设备(10﹣m)台,
根据题意得:12m+10(10﹣m)≤105,
解得:m≤ ,
∴m可取的值为0,1,2.
故有3种购买方案,方案1:购买B型设备10台;方案2:购买A型设备1台,B型设备9台;方案3:购买A型设备2台,B型设备8台.
(3)当m=0时,每月的污水处理量为:200×10=2000(吨),
∵2000<2040,
∴m=0不合题意,舍去;
当m=1时,每月的污水处理量为:240+200×9=2040(吨),
∵2040=2040,
∴m=1符合题意,此时购买设备所需资金为:12+10×9=102(万元);
当m=2时,每月的污水处理量为:240×2+200×8=2080(吨),
∵2080>2040,
∴m=2符合题意,此时购买设备所需资金为:12×2+10×8=104(万元).
∵102<104,
∴为了节约资金,该公司最省钱的一种购买方案为:购买A型设备1台,B型设备9台.
【点睛】
考查了二元一次方程组的应用以及一元一次不等式的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式;(3)由每月要求处理污水量来确定m可取的值.
