第十二章 全等三角形单元测试卷(含答案)
文档属性
| 名称 | 第十二章 全等三角形单元测试卷(含答案) | 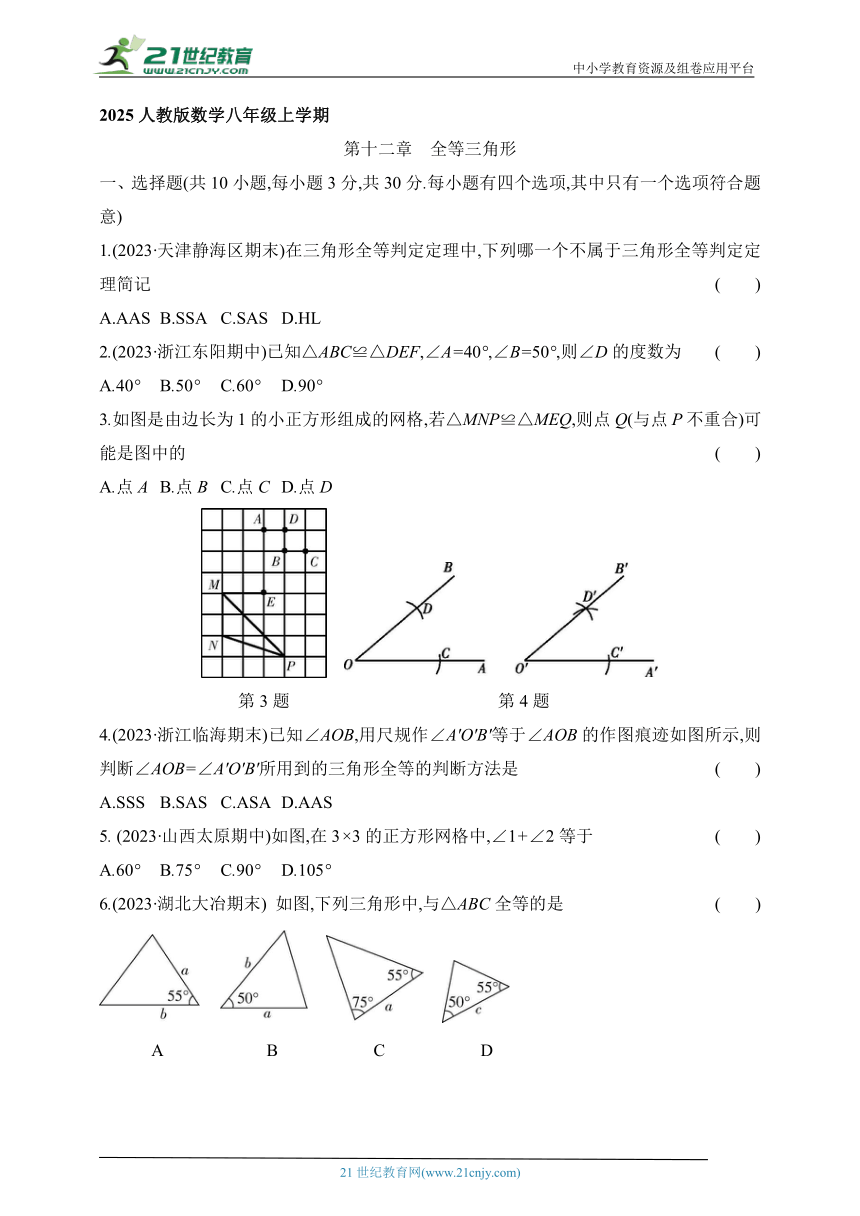 | |
| 格式 | docx | ||
| 文件大小 | 584.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 15:45:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教版数学八年级上学期
第十二章 全等三角形
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2023·天津静海区期末)在三角形全等判定定理中,下列哪一个不属于三角形全等判定定理简记 ( )
A.AAS B.SSA C.SAS D.HL
2.(2023·浙江东阳期中)已知△ABC≌△DEF,∠A=40°,∠B=50°,则∠D的度数为 ( )
A.40° B.50° C.60° D.90°
3.如图是由边长为1的小正方形组成的网格,若△MNP≌△MEQ,则点Q(与点P不重合)可能是图中的 ( )
A.点A B.点B C.点C D.点D
第3题 第4题
4.(2023·浙江临海期末)已知∠AOB,用尺规作∠A'O'B'等于∠AOB的作图痕迹如图所示,则判断∠AOB=∠A'O'B'所用到的三角形全等的判断方法是 ( )
A.SSS B.SAS C.ASA D.AAS
5. (2023·山西太原期中)如图,在3×3的正方形网格中,∠1+∠2等于 ( )
A.60° B.75° C.90° D.105°
6.(2023·湖北大冶期末) 如图,下列三角形中,与△ABC全等的是 ( )
A B C D
第5题 第6题 第7题
7.(2023·河北廊坊安次区期末)嘉琪在解决问题时,给出的推理过程如下:
如图,点D在AC上,点E在AB上,AB=AC,∠B=∠C.
求证:CD=BE.
证明:在△ADB和△AEC中,
∴△ADB≌△AEC,
∴CD=BE.
小明为了保证嘉琪的推理更严谨,想在方框中“∴△ADB≌△AEC,”和“∴CD=BE.”之间作补充,下列说法正确的是 ( )
A.嘉琪的推理严谨,不需要补充 B.应补充“∴AD=AE,”
C.应补充“∴AB=AC,” D.应补充“∴CE=BD,”
8.(2022·江苏苏州模拟)如图,在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,
DE⊥AB于点E,且AB=5 cm,AC=3 cm,BC=4 cm,则△DEB的周长为 ( )
A.6 cm B.5 cm C.7 cm D.8 cm
9.(2023·山东泰安泰山区期末)如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,
∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD= ( )
A.110° B.125° C.130° D.155°
第8题 第9题 第10题
10.(2023·陕西汉中期末)如图,OA平分∠NOP,OB平分∠MOP,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )
A.AD+BC=AB B.点O是CD的中点 C.∠AOB=90° D.∠CBO=∠BAO
二、填空题(共6小题,每小题3分,共18分)
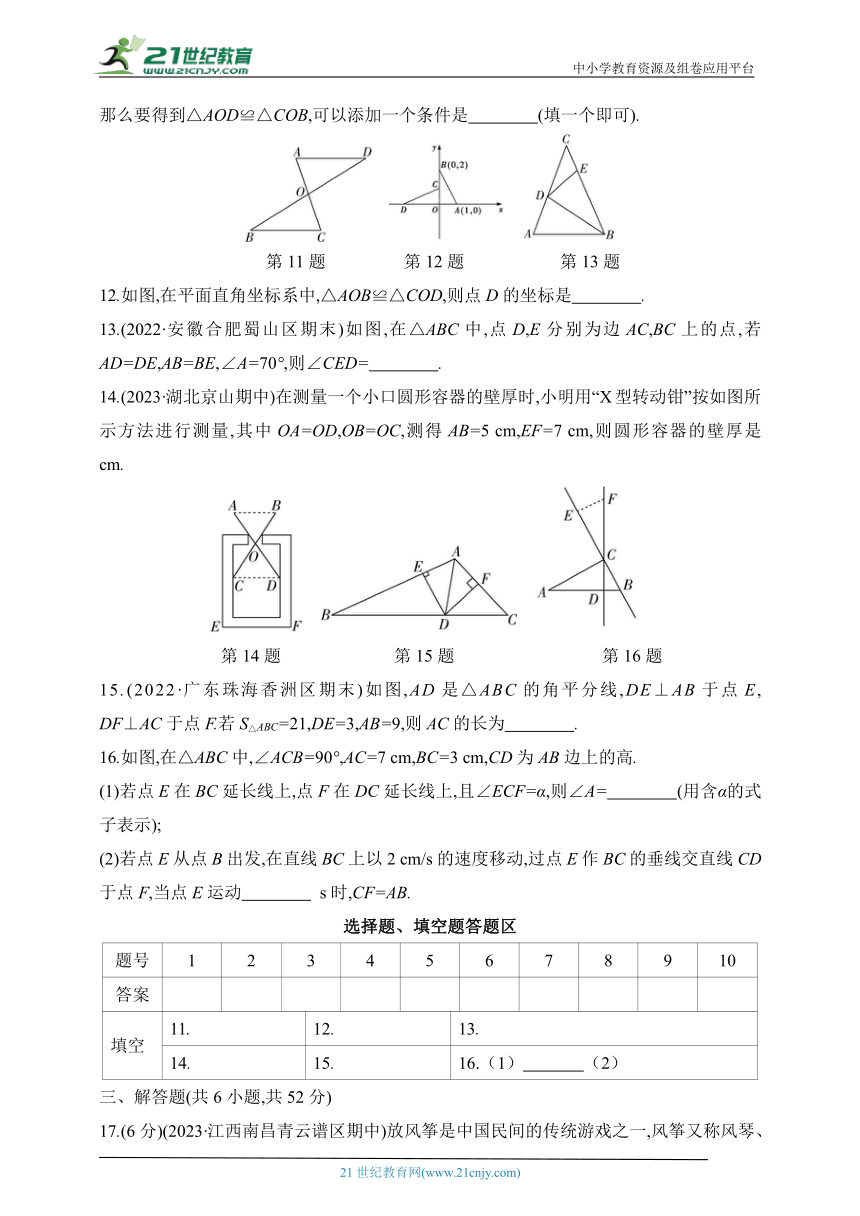
11.[中考创新题型|开放性试题](2023·北京顺义区期末)如图,AC与BD相交于点O,OA=OC,那么要得到△AOD≌△COB,可以添加一个条件是 (填一个即可).
第11题 第12题 第13题
12.如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是 .
13.(2022·安徽合肥蜀山区期末)如图,在△ABC中,点D,E分别为边AC,BC上的点,若AD=DE,AB=BE,∠A=70°,则∠CED= .
14.(2023·湖北京山期中)在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图所示方法进行测量,其中OA=OD,OB=OC,测得AB=5 cm,EF=7 cm,则圆形容器的壁厚是 cm.
第14题 第15题 第16题
15.(2022·广东珠海香洲区期末)如图,AD是△ABC的角平分线,DE⊥AB于点E,
DF⊥AC于点F.若S△ABC=21,DE=3,AB=9,则AC的长为 .
16.如图,在△ABC中,∠ACB=90°,AC=7 cm,BC=3 cm,CD为AB边上的高.
(1)若点E在BC延长线上,点F在DC延长线上,且∠ECF=α,则∠A= (用含α的式子表示);
(2)若点E从点B出发,在直线BC上以2 cm/s的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动 s时,CF=AB.
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.(1) (2)
三、解答题(共6小题,共52分)
17.(6分)(2023·江西南昌青云谱区期中)放风筝是中国民间的传统游戏之一,风筝又称风琴、纸鹞、鹞子、纸鸢.如图(1),小华制作了一个风筝,示意图如图(2)所示,
AB=AC,DB=DC,他发现AD不仅平分∠BAC,而且平分∠BDC,你觉得他的发现正确吗 请说明理由.
18.(6分)如图,点C,F在线段BE上,∠ABC=∠DEF=90°,BC=EF,请添加一个合适的条件使△ABC≌△DEF.
(1)根据“ASA”进行判定,需添加的条件是 ;根据“HL”进行判定,需添加的条件是 .
(2)请从(1)中选择一种,加以证明.
19.(9分)(2023·天津红桥区期末改编)如图,在△ABC中,AD是△ABC的中线,DE⊥
AB,DF⊥AC,垂足分别为E,F.
(1)若BE=CF,求证:AD是△ABC的角平分线.
(2)若AD是△ABC的角平分线,求证:BE=CF.
20.(9分)(2022·山东聊城期末)课间,小明拿着老师的等腰直角三角板(AC=CB,AC⊥BC)玩,不小心掉到两墙之间(墙与地面垂直),三角板的直角顶点恰好着地,且D,C,E三点在同一直线上,如图所示.(A,B,C,D,E五点在同一平面内)
(1)求证:△ADC≌△CEB.
(2)已知DE=35 cm,且图中每块砌墙砖的厚度均为a cm,请你帮小明求出每块砌墙砖的厚度.
21.(11分)(2023·山东淄博周村区期中)在△ABC中,AB=AC,点D是线段CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图(1),当点D在线段CB上,∠BAC=90°时,∠DCE= °.
(2)设∠BAC=α,∠DCE=β.如图(2),当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论.
图(1) 图(2)
22.(11分)(2023·江苏南京一中月考)如图,已知△ABC和△A'B'C',D,D'分别为BC,
B'C'的中点,且AD=A'D',AB=A'B'.
(1)当∠BAC=∠B'A'C'=90°时,求证:△ABC≌△A'B'C'.
(2)当BD=B'D'时,求证:△ABC≌△A'B'C'.证明的途径可以用下面的框图表示,请填写其中的空格.
(3)当AC=A'C'时,求证:△ABC≌△A'B'C'.
第十二章 全等三角形
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A D A C B B A C D
11.OD=OB(答案不唯一) 12.(-2,0) 13.110°
14.1 15.5 16.(1)α (2)2或5
1.B
2.A ∵△ABC≌△DEF,∠A=40°,∴∠D=∠A=40°.
3.D
4.A 如图,连接CD,C'D',因为在△COD和△C'O'D'中,CO=C'O',DO=D'O',CD=C'D',所以△COD≌△C'O'D'(SSS),所以∠AOB=∠A'O'B'.故选A.
5.C如图,∵AC=DE,∠ACB=∠DEF,BC=FE,∴△ACB≌△DEF(SAS),∴∠1=∠FDE.
∵∠FDE+∠2=90°,∴∠1+∠2=90°.
6.B ∵∠A=55°,∠B=75°,∴∠C=50°.根据“SAS”(两边和它们的夹角分别对应相等)可以判定B选项中的三角形与△ABC全等.
证明三角形全等的技巧
7.B ∵△ADB≌△AEC,∴AD=AE,∵AC=AB,∴AC-AD=AB-AE,∴CD=BE,∴应该补充“∴AD=AE,”.
8.A ∵AD平分∠CAB交BC于点D,DE⊥AB,DC⊥AC,∴DC=DE.在Rt△ADC和Rt△ADE
中,∴Rt△ADC≌Rt△ADE(HL),∴AE=AC=3 ,∴BE=AB-AE=5-3=2(cm),
∴△DEB的周长=BE+BD+DE=BE+BD+CD=BE+BC=2+4=6(cm).
9.C 在△ACD和△BCE中,∴△ACD≌△BCE(SSS),∴∠ACD=∠BCE,∠A=∠B,
∴∠ABC+∠ACE=∠ACE+∠ECD,∴∠ACB=∠ECD=(∠BCD-∠ACE)=×(155°-55°)=
50°.∵∠B+∠ACB=∠A+∠APB,∴∠APB=∠ACB=50°,∴∠BPD=180°-50°=130°.
10.D (排除法)∵OA平分∠NOP,OB平分∠MOP,∴∠AOD=∠AOP=∠DOE,∠COB=
∠EOB=∠COE,∴∠AOB=(∠COE+∠DOE)=90°,故选项C不合题意.在△AOD和△AOE中,∴△AOD≌△AOE(AAS),∴AE=AD,OE=OD,∠OAE=∠OAD.同理可得BC=
BE,CO=OE,∴AB=AE+BE=AD+BC,CO=OE=OD,∴点O是CD的中点,故选项A,B不合题意.选D.
11.OD=OB(答案不唯一) ∵ OD=OB,OA=OC,∠AOD=∠COB,∴△AOD≌△COB(SAS).
12.(-2,0) ∵△AOB≌△COD,∴OD=OB=2,∴点D的坐标是(-2,0).
13.110° 在△ADB与△EDB中,∴△ADB≌△EDB(SSS),∴∠DEB=∠A=70°,
∴∠CED=180°-∠DEB=110°.
14.1 在△COD和△BOA中,∴△COD≌△BOA(SAS),∴CD=AB=5 cm,∴圆形容器的壁厚为(EF-CD)=×(7-5)=1(cm).
15.5 ∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DF=DE=3∵S△ABD+S△ACD=S△ABC,
∴·AB·DE+·AC·DF=21,即×9×3+×AC×3=21,∴AC=5.
16.(1)α (2)2或5 (1)∵∠ACB=90°,∴∠A+∠CBD=90°.∵CD为AB边上的高,
∴∠CDB=90°,∴∠BCD+∠CBD=90°,∴∠A=∠BCD.∵∠BCD=∠ECF,∴∠A=∠ECF=α.(2)∵过点E作BC的垂线交直线CD于点F,∴∠CEF=90°=∠ACB,在△CEF和△ACB中,∴△CEF≌△ACB(AAS),∴CE=AC=7 cm.①如图,当点E在射线BC上时,BE=CE+BC=7+3=10(cm).∵点E从点B出发,在直线BC上以2 cm/s的速度移动,∴E移动了10÷2=5(s).②当点E在射线CB上时,记为E',BE'=CE'-BC=7-3=
4(cm).∵点E从点B出发,在直线BC上以2 cm/s的速度移动,∴E移动了4÷2=2(s).综上所述,当点E移动5 s或2 s时,CF=AB.
17.【参考答案】正确. (2分)
理由如下:
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠BDA=∠CDA,
即AD不仅平分∠BAC,而且平分∠BDC,
∴他的发现正确. (6分)
18.【参考答案】(1)∠ACB=∠DFE AC=DF (4分)
(2)选择添加条件AC=DF.
证明:∵∠ABC=∠DEF=90°,
∴在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL). (6分)
(2)选择添加条件∠ACB=∠DFE.
证明:在△ABC和△DEF中,
∴△ABC≌△DEF(ASA). (6分)
19.【参考答案】证明:(1)∵AD是△ABC的中线,
∴BD=CD.
∵DE⊥AB,DF⊥AC,
∴△BDE,△CDF都是直角三角形.
在Rt△BDE与Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF. (2分)
∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.(4分)
(2)∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF.
∵AD是△ABC的中线,∴BD=CD. (6分)
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),∴BE=CF. (9分)
20.【参考答案】(1)证明:由题意得AC=BC,∠ACB=90°,∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠BCE=∠CAD
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS). (5分)
(2)由题意知,每块砌墙砖的厚度均为a cm,
∴AD=4a cm,BE=3a cm.
由(1)得△ADC≌△CEB,
∴DC=BE=3a cm,CE=AD=4a cm,
∴DE=DC+CE=7a=35(cm),解得a=5.
答:每块砌墙砖的厚度均为5 cm. (9分)
21.【参考答案】(1)90 (4分)
解法提示:∵∠BAD+∠DAC=90°,∠DAC+∠CAE=90°,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),∴∠ACE=∠B.
∵∠B+∠ACB=90°,∴∠DCE=∠ACE+∠ACB=90°.
(2)α+β=180°.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE. (6分)
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS), (8分)
∴∠B=∠ACE.
∵∠B+∠ACB=180°-α,
∴∠DCE=∠ACE+∠ACB=∠B+∠ACB=180°-α=β,
∴α+β=180°. (11分)
22.【参考答案】(1)证明:∵∠BAC=90°,点D为BC的中点,
∴AD=BC,
同理可得A'D'=B'C'.
∵AD=A'D',∴BC=B'C'.
在Rt△ABC和Rt△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'(HL). (3分)
(2)①∠B=∠B'
②BD=BC ③B'D'=B'C' ④SAS (7分)
(3)证明:如图,延长AD至点E,使得DE=DA,连接BE,延长A'D'至点E',使得D'E'=D'A',连接B'E',
∵AD=A'D',∴AE=A'E'.
在△ADC和△EDB中,
∴△ADC≌△EDB(SAS),
∴AC=BE,∠CAD=∠E.
同理可得△A'D'C'≌△E'D'B'(SAS),
∴A'C'=B'E',∠C'A'D'=∠E'.
∵AC=A'C',∴BE=B'E'.
在△BAE和△B'A'E'中,
∴△BAE≌△B'A'E'(SSS),∴∠BAD=∠B'A'D',∠E=∠E',
∴∠CAD=∠C'A'D',
∴∠BAC=∠B'A'C'.
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SAS). (11分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教版数学八年级上学期
第十二章 全等三角形
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2023·天津静海区期末)在三角形全等判定定理中,下列哪一个不属于三角形全等判定定理简记 ( )
A.AAS B.SSA C.SAS D.HL
2.(2023·浙江东阳期中)已知△ABC≌△DEF,∠A=40°,∠B=50°,则∠D的度数为 ( )
A.40° B.50° C.60° D.90°
3.如图是由边长为1的小正方形组成的网格,若△MNP≌△MEQ,则点Q(与点P不重合)可能是图中的 ( )
A.点A B.点B C.点C D.点D
第3题 第4题
4.(2023·浙江临海期末)已知∠AOB,用尺规作∠A'O'B'等于∠AOB的作图痕迹如图所示,则判断∠AOB=∠A'O'B'所用到的三角形全等的判断方法是 ( )
A.SSS B.SAS C.ASA D.AAS
5. (2023·山西太原期中)如图,在3×3的正方形网格中,∠1+∠2等于 ( )
A.60° B.75° C.90° D.105°
6.(2023·湖北大冶期末) 如图,下列三角形中,与△ABC全等的是 ( )
A B C D
第5题 第6题 第7题
7.(2023·河北廊坊安次区期末)嘉琪在解决问题时,给出的推理过程如下:
如图,点D在AC上,点E在AB上,AB=AC,∠B=∠C.
求证:CD=BE.
证明:在△ADB和△AEC中,
∴△ADB≌△AEC,
∴CD=BE.
小明为了保证嘉琪的推理更严谨,想在方框中“∴△ADB≌△AEC,”和“∴CD=BE.”之间作补充,下列说法正确的是 ( )
A.嘉琪的推理严谨,不需要补充 B.应补充“∴AD=AE,”
C.应补充“∴AB=AC,” D.应补充“∴CE=BD,”
8.(2022·江苏苏州模拟)如图,在△ABC中,∠C=90°,AD平分∠CAB交BC于点D,
DE⊥AB于点E,且AB=5 cm,AC=3 cm,BC=4 cm,则△DEB的周长为 ( )
A.6 cm B.5 cm C.7 cm D.8 cm
9.(2023·山东泰安泰山区期末)如图,在△ACD和△BCE中,AC=BC,AD=BE,CD=CE,
∠ACE=55°,∠BCD=155°,AD与BE相交于点P,则∠BPD= ( )
A.110° B.125° C.130° D.155°
第8题 第9题 第10题
10.(2023·陕西汉中期末)如图,OA平分∠NOP,OB平分∠MOP,AB⊥OP于点E,BC⊥MN于点C,AD⊥MN于点D,下列结论错误的是( )
A.AD+BC=AB B.点O是CD的中点 C.∠AOB=90° D.∠CBO=∠BAO
二、填空题(共6小题,每小题3分,共18分)
11.[中考创新题型|开放性试题](2023·北京顺义区期末)如图,AC与BD相交于点O,OA=OC,那么要得到△AOD≌△COB,可以添加一个条件是 (填一个即可).
第11题 第12题 第13题
12.如图,在平面直角坐标系中,△AOB≌△COD,则点D的坐标是 .
13.(2022·安徽合肥蜀山区期末)如图,在△ABC中,点D,E分别为边AC,BC上的点,若AD=DE,AB=BE,∠A=70°,则∠CED= .
14.(2023·湖北京山期中)在测量一个小口圆形容器的壁厚时,小明用“X型转动钳”按如图所示方法进行测量,其中OA=OD,OB=OC,测得AB=5 cm,EF=7 cm,则圆形容器的壁厚是 cm.
第14题 第15题 第16题
15.(2022·广东珠海香洲区期末)如图,AD是△ABC的角平分线,DE⊥AB于点E,
DF⊥AC于点F.若S△ABC=21,DE=3,AB=9,则AC的长为 .
16.如图,在△ABC中,∠ACB=90°,AC=7 cm,BC=3 cm,CD为AB边上的高.
(1)若点E在BC延长线上,点F在DC延长线上,且∠ECF=α,则∠A= (用含α的式子表示);
(2)若点E从点B出发,在直线BC上以2 cm/s的速度移动,过点E作BC的垂线交直线CD于点F,当点E运动 s时,CF=AB.
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.(1) (2)
三、解答题(共6小题,共52分)
17.(6分)(2023·江西南昌青云谱区期中)放风筝是中国民间的传统游戏之一,风筝又称风琴、纸鹞、鹞子、纸鸢.如图(1),小华制作了一个风筝,示意图如图(2)所示,
AB=AC,DB=DC,他发现AD不仅平分∠BAC,而且平分∠BDC,你觉得他的发现正确吗 请说明理由.
18.(6分)如图,点C,F在线段BE上,∠ABC=∠DEF=90°,BC=EF,请添加一个合适的条件使△ABC≌△DEF.
(1)根据“ASA”进行判定,需添加的条件是 ;根据“HL”进行判定,需添加的条件是 .
(2)请从(1)中选择一种,加以证明.
19.(9分)(2023·天津红桥区期末改编)如图,在△ABC中,AD是△ABC的中线,DE⊥
AB,DF⊥AC,垂足分别为E,F.
(1)若BE=CF,求证:AD是△ABC的角平分线.
(2)若AD是△ABC的角平分线,求证:BE=CF.
20.(9分)(2022·山东聊城期末)课间,小明拿着老师的等腰直角三角板(AC=CB,AC⊥BC)玩,不小心掉到两墙之间(墙与地面垂直),三角板的直角顶点恰好着地,且D,C,E三点在同一直线上,如图所示.(A,B,C,D,E五点在同一平面内)
(1)求证:△ADC≌△CEB.
(2)已知DE=35 cm,且图中每块砌墙砖的厚度均为a cm,请你帮小明求出每块砌墙砖的厚度.
21.(11分)(2023·山东淄博周村区期中)在△ABC中,AB=AC,点D是线段CB上的一动点(不与点B,C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE=∠BAC,连接CE.
(1)如图(1),当点D在线段CB上,∠BAC=90°时,∠DCE= °.
(2)设∠BAC=α,∠DCE=β.如图(2),当点D在线段CB上,∠BAC≠90°时,请你探究α与β之间的数量关系,并证明你的结论.
图(1) 图(2)
22.(11分)(2023·江苏南京一中月考)如图,已知△ABC和△A'B'C',D,D'分别为BC,
B'C'的中点,且AD=A'D',AB=A'B'.
(1)当∠BAC=∠B'A'C'=90°时,求证:△ABC≌△A'B'C'.
(2)当BD=B'D'时,求证:△ABC≌△A'B'C'.证明的途径可以用下面的框图表示,请填写其中的空格.
(3)当AC=A'C'时,求证:△ABC≌△A'B'C'.
第十二章 全等三角形
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
B A D A C B B A C D
11.OD=OB(答案不唯一) 12.(-2,0) 13.110°
14.1 15.5 16.(1)α (2)2或5
1.B
2.A ∵△ABC≌△DEF,∠A=40°,∴∠D=∠A=40°.
3.D
4.A 如图,连接CD,C'D',因为在△COD和△C'O'D'中,CO=C'O',DO=D'O',CD=C'D',所以△COD≌△C'O'D'(SSS),所以∠AOB=∠A'O'B'.故选A.
5.C如图,∵AC=DE,∠ACB=∠DEF,BC=FE,∴△ACB≌△DEF(SAS),∴∠1=∠FDE.
∵∠FDE+∠2=90°,∴∠1+∠2=90°.
6.B ∵∠A=55°,∠B=75°,∴∠C=50°.根据“SAS”(两边和它们的夹角分别对应相等)可以判定B选项中的三角形与△ABC全等.
证明三角形全等的技巧
7.B ∵△ADB≌△AEC,∴AD=AE,∵AC=AB,∴AC-AD=AB-AE,∴CD=BE,∴应该补充“∴AD=AE,”.
8.A ∵AD平分∠CAB交BC于点D,DE⊥AB,DC⊥AC,∴DC=DE.在Rt△ADC和Rt△ADE
中,∴Rt△ADC≌Rt△ADE(HL),∴AE=AC=3 ,∴BE=AB-AE=5-3=2(cm),
∴△DEB的周长=BE+BD+DE=BE+BD+CD=BE+BC=2+4=6(cm).
9.C 在△ACD和△BCE中,∴△ACD≌△BCE(SSS),∴∠ACD=∠BCE,∠A=∠B,
∴∠ABC+∠ACE=∠ACE+∠ECD,∴∠ACB=∠ECD=(∠BCD-∠ACE)=×(155°-55°)=
50°.∵∠B+∠ACB=∠A+∠APB,∴∠APB=∠ACB=50°,∴∠BPD=180°-50°=130°.
10.D (排除法)∵OA平分∠NOP,OB平分∠MOP,∴∠AOD=∠AOP=∠DOE,∠COB=
∠EOB=∠COE,∴∠AOB=(∠COE+∠DOE)=90°,故选项C不合题意.在△AOD和△AOE中,∴△AOD≌△AOE(AAS),∴AE=AD,OE=OD,∠OAE=∠OAD.同理可得BC=
BE,CO=OE,∴AB=AE+BE=AD+BC,CO=OE=OD,∴点O是CD的中点,故选项A,B不合题意.选D.
11.OD=OB(答案不唯一) ∵ OD=OB,OA=OC,∠AOD=∠COB,∴△AOD≌△COB(SAS).
12.(-2,0) ∵△AOB≌△COD,∴OD=OB=2,∴点D的坐标是(-2,0).
13.110° 在△ADB与△EDB中,∴△ADB≌△EDB(SSS),∴∠DEB=∠A=70°,
∴∠CED=180°-∠DEB=110°.
14.1 在△COD和△BOA中,∴△COD≌△BOA(SAS),∴CD=AB=5 cm,∴圆形容器的壁厚为(EF-CD)=×(7-5)=1(cm).
15.5 ∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DF=DE=3∵S△ABD+S△ACD=S△ABC,
∴·AB·DE+·AC·DF=21,即×9×3+×AC×3=21,∴AC=5.
16.(1)α (2)2或5 (1)∵∠ACB=90°,∴∠A+∠CBD=90°.∵CD为AB边上的高,
∴∠CDB=90°,∴∠BCD+∠CBD=90°,∴∠A=∠BCD.∵∠BCD=∠ECF,∴∠A=∠ECF=α.(2)∵过点E作BC的垂线交直线CD于点F,∴∠CEF=90°=∠ACB,在△CEF和△ACB中,∴△CEF≌△ACB(AAS),∴CE=AC=7 cm.①如图,当点E在射线BC上时,BE=CE+BC=7+3=10(cm).∵点E从点B出发,在直线BC上以2 cm/s的速度移动,∴E移动了10÷2=5(s).②当点E在射线CB上时,记为E',BE'=CE'-BC=7-3=
4(cm).∵点E从点B出发,在直线BC上以2 cm/s的速度移动,∴E移动了4÷2=2(s).综上所述,当点E移动5 s或2 s时,CF=AB.
17.【参考答案】正确. (2分)
理由如下:
在△ABD和△ACD中,
∴△ABD≌△ACD(SSS),
∴∠BAD=∠CAD,∠BDA=∠CDA,
即AD不仅平分∠BAC,而且平分∠BDC,
∴他的发现正确. (6分)
18.【参考答案】(1)∠ACB=∠DFE AC=DF (4分)
(2)选择添加条件AC=DF.
证明:∵∠ABC=∠DEF=90°,
∴在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL). (6分)
(2)选择添加条件∠ACB=∠DFE.
证明:在△ABC和△DEF中,
∴△ABC≌△DEF(ASA). (6分)
19.【参考答案】证明:(1)∵AD是△ABC的中线,
∴BD=CD.
∵DE⊥AB,DF⊥AC,
∴△BDE,△CDF都是直角三角形.
在Rt△BDE与Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),
∴DE=DF. (2分)
∵DE⊥AB,DF⊥AC,
∴AD是△ABC的角平分线.(4分)
(2)∵AD是△ABC的角平分线,DE⊥AB,DF⊥AC,∴DE=DF.
∵AD是△ABC的中线,∴BD=CD. (6分)
在Rt△BDE和Rt△CDF中,
∴Rt△BDE≌Rt△CDF(HL),∴BE=CF. (9分)
20.【参考答案】(1)证明:由题意得AC=BC,∠ACB=90°,∠ADC=∠CEB=90°,
∴∠ACD+∠BCE=90°,∠ACD+∠CAD=90°,
∴∠BCE=∠CAD
在△ADC和△CEB中,
∴△ADC≌△CEB(AAS). (5分)
(2)由题意知,每块砌墙砖的厚度均为a cm,
∴AD=4a cm,BE=3a cm.
由(1)得△ADC≌△CEB,
∴DC=BE=3a cm,CE=AD=4a cm,
∴DE=DC+CE=7a=35(cm),解得a=5.
答:每块砌墙砖的厚度均为5 cm. (9分)
21.【参考答案】(1)90 (4分)
解法提示:∵∠BAD+∠DAC=90°,∠DAC+∠CAE=90°,
∴∠BAD=∠CAE.
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS),∴∠ACE=∠B.
∵∠B+∠ACB=90°,∴∠DCE=∠ACE+∠ACB=90°.
(2)α+β=180°.
证明:∵∠BAC=∠DAE,
∴∠BAC-∠DAC=∠DAE-∠DAC,
∴∠BAD=∠CAE. (6分)
在△BAD和△CAE中,
∴△BAD≌△CAE(SAS), (8分)
∴∠B=∠ACE.
∵∠B+∠ACB=180°-α,
∴∠DCE=∠ACE+∠ACB=∠B+∠ACB=180°-α=β,
∴α+β=180°. (11分)
22.【参考答案】(1)证明:∵∠BAC=90°,点D为BC的中点,
∴AD=BC,
同理可得A'D'=B'C'.
∵AD=A'D',∴BC=B'C'.
在Rt△ABC和Rt△A'B'C'中,
∴Rt△ABC≌Rt△A'B'C'(HL). (3分)
(2)①∠B=∠B'
②BD=BC ③B'D'=B'C' ④SAS (7分)
(3)证明:如图,延长AD至点E,使得DE=DA,连接BE,延长A'D'至点E',使得D'E'=D'A',连接B'E',
∵AD=A'D',∴AE=A'E'.
在△ADC和△EDB中,
∴△ADC≌△EDB(SAS),
∴AC=BE,∠CAD=∠E.
同理可得△A'D'C'≌△E'D'B'(SAS),
∴A'C'=B'E',∠C'A'D'=∠E'.
∵AC=A'C',∴BE=B'E'.
在△BAE和△B'A'E'中,
∴△BAE≌△B'A'E'(SSS),∴∠BAD=∠B'A'D',∠E=∠E',
∴∠CAD=∠C'A'D',
∴∠BAC=∠B'A'C'.
在△ABC和△A'B'C'中,
∴△ABC≌△A'B'C'(SAS). (11分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
