第十三章 轴对称单元测试卷(含答案)
文档属性
| 名称 | 第十三章 轴对称单元测试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 558.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 00:00:00 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
2025人教版数学八年级上学期
第十三章 轴对称
时间 60分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2023·北京燕山区期末)在数学活动课中,同学们利用几何画板绘制出了下列曲线,其中不是轴对称图形的是 ( )
A.等角螺旋线 B.心形线 C.四叶玫瑰线 D.蝴蝶曲线
2.(2023·山东菏泽定陶区期中)已知点P(2,a)与Q(2,b)关于x轴对称,则a+b= ( )
A.1 B.0 C.4 D.2
3.(2023·山东聊城期末)甲、乙、丙三地如图所示,若想建立一个货物中转仓,使其到甲、乙、丙三地的距离相等,则中转仓的位置应选在 ( )
A.三条角平分线的交点处 B.三边垂直平分线的交点处
C.三边中线的交点处 D.三边上的高的交点处
第3题 第4题 第6题
4.(2023·山西晋中期中)如图,一个小孩坐在秋千上,若秋千绕点O旋转了86°,小孩的位置也从A点运动到了A'点,则∠OA'A的度数为 ( )
A.33° B.37° C.43° D.47°
5.(2023·浙江宁波海曙区期末)已知等腰三角形的一个内角为50°,则它的顶角为 ( )
A.50° B.80° C.65°或80° D.50°或80°
6.(2023·河南潢川期末)如图,已知等边三角形ABC的周长为a,BD⊥BC,AD⊥BD,则AD等于 ( )
A.a B.a C.a D.
7.如图,直线a,b相交形成的角中,锐角为52°,交点为O,点A在直线a上,直线b上存在点B,使以点O,A,B为顶点的三角形是等腰三角形,这样的点B有 ( )
A.4个 B.3个 C.2个 D.1个
第7题 第8题
8.(2022·广东广州天河区期末)在△ABC中,AB=AC,∠A=36°,若按如图所示的尺规作图方法作出线段BD,则下列结论错误的是 ( )
A.AD=BD B.∠BDC=72°
C.S△ABD∶S△BCD=BC∶AC D.△BCD的周长=AB+BC
9.(2023·河北唐山十二中期末)如图,∠AOB=60°,点P在射线OA上,OP=22,点M,N在射线OB上(点M在点N的左侧),且PM=PN.若MN=4,则OM的长为 ( )
A.7 B.8 C.9 D.11
第9题 第10题
10.(2023·辽宁大连金普新区期末)如图,∠ABC=30°,点D是∠ABC内部的一点,连接BD.若BD=1m,点E,F分别是BA,BC上的动点,则△DEF的周长的最小值为 ( )
A.0.5m B.1m C.1.5m D.2m
二、填空题(本大题共6小题,每小题3分,共18分)
11.(2023·北京燕山区期末)已知Rt△ABC中,∠C=90°,∠A=60°,AB=8,则
AC= .
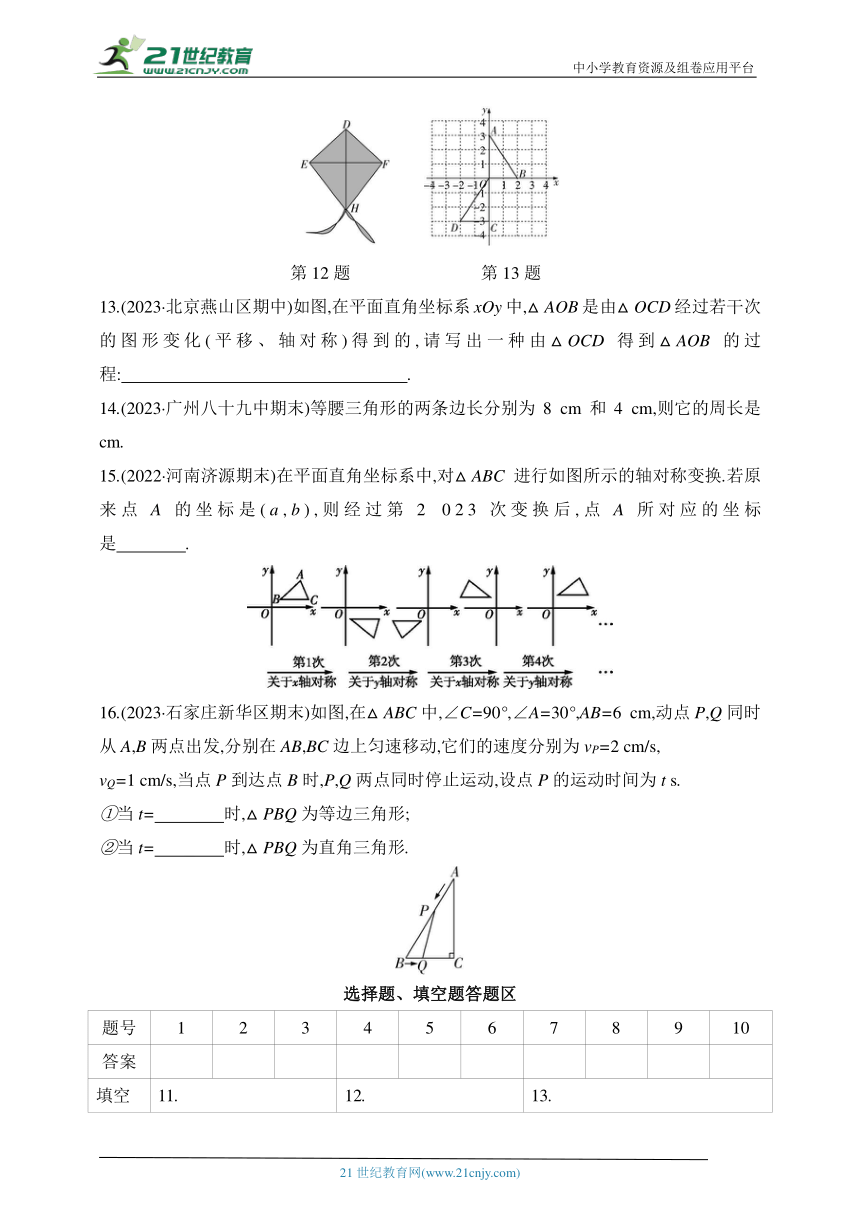
12.(2023·广西南宁期中)小军做了一个如图所示的风筝,其中EH=FH,ED=FD,则DH是EF的 线.
第12题 第13题
13.(2023·北京燕山区期中)如图,在平面直角坐标系xOy中,△AOB是由△OCD经过若干次的图形变化(平移、轴对称)得到的,请写出一种由△OCD得到△AOB的过程: .
14.(2023·广州八十九中期末)等腰三角形的两条边长分别为8 cm和4 cm,则它的周长是 cm.
15.(2022·河南济源期末)在平面直角坐标系中,对△ABC进行如图所示的轴对称变换.若原来点A的坐标是(a,b),则经过第2 023次变换后,点A所对应的坐标
是 .
16.(2023·石家庄新华区期末)如图,在△ABC中,∠C=90°,∠A=30°,AB=6 cm,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为vP=2 cm/s,
vQ=1 cm/s,当点P到达点B时,P,Q两点同时停止运动,设点P的运动时间为t s.
①当t= 时,△PBQ为等边三角形;
②当t= 时,△PBQ为直角三角形.
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.① ②
三、解答题(共6小题,共52分)
17.(6分)(2023·河南漯河郾城区期中)如图,在△ABC中,AB=AC,∠A=120°,DE垂直平分AB于D,交BC于E点,求证:CE=2BE.
18.(8分)(2023·北京通州区期末)如图是4×4正方形网格,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使整个涂成黑色的图形为轴对称图形.请补全图形,并且画出对称轴(如图例),要求所画的四种方案不能重复.
19.(8分)(2022·湖北十堰郧阳区期中改编)某市发生地震后,为了抢救伤员,一架救援直升机从该市A地起飞,运送一批地震伤员沿正北方向到机场N,如图.上午8时,直升机从A地出发,以200 km/h的速度向正北方向飞行,9时到达B地,此时,机场的导航站传来信息:在C处有一座高山,因受天气影响,高山周围80 km内能见度低,飞行时会遇到危险.经测量得∠NAC=15°,∠NBC=30°.问该直升机继续向机场N飞行是否有危险,请说明理由.
20.(8分)(2023·北京二十中月考)如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,点E,F分别为垂足.
(1)求证:△DEF是等腰三角形.
(2)当∠A的度数为 时,△DEF是等边三角形.
21.(10分)(2022·河北石家庄裕华区期末)
【问题】
如图,在△ABC中,点D为BC边上一点,BD=BA.EF垂直平分AC,交AC于点E,交BC于点F,连接AD,AF.若∠B=30°,∠BAF=90°,求∠DAC的度数.
【探究】
如果把【问题】中的条件“∠B=30°”去掉,其他条件不变,那么∠DAC的度数会变吗 请说明理由.
22.(12分)(2023·安徽合肥蜀山区期末)下面是“已知斜边作一个直角三角形”的尺规作图过程.
已知:线段AB.
求作:一个直角三角形ABC,使线段AB为斜边.
作法:①过点A任意作一条射线l;
②在射线l上任取两点D,E;
③分别以点D,E为圆心,DB,EB长为半径作弧,两弧相交于点P;
④作射线BP交射线l于点C.
则△ABC就是所求作的直角三角形.
(1)使用直尺和圆规,在图(1)中依作法补全图形(保留作图痕迹).
(2)证明:连接DP,EP,
∵DB= ,
∴点D在线段BP的垂直平分线上.( )(填推理的依据)
同理可证,点E在线段BP的垂直平分线上.
根据两点确定一条直线,可知DE是线段BP的垂直平分线.
∴∠ACB=90°.
(3)如图(2),在Rt△ABC中,∠ACB=90°,∠A=30°.
猜想BC与AB满足的数量关系,并证明.
图(1) 图(2)
第十三章 轴对称
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
A B B D D B A C C B
11.4 12.垂直平分 13.先将△OCD关于y轴对称,再向上平移3个单位长度得到△AOB(答案不唯一)
14.20 15.(-a,b) 16.(1)2 (2)或
1.A
2.B ∵点P(2,a)与Q(2,b)关于x轴对称,∴a+b=0.
3.B 【点拨】线段的垂直平分线上的点到线段的两个端点的距离相等
4.D ∵秋千绕点O旋转了86°,小孩的位置也从A点运动到了A'点,∴∠AOA'=
86°,OA=OA',∴∠OA'A=×(180°-86°)=47°.
5.D 在△ABC中,AB=AC.分两种情况:①顶角∠A=50°.②当底角是50°时,
∵AB=AC,∴∠B=∠C=50°.∵∠A+∠B+∠C=180°,∴∠A=180°-50°-50°=80°.∴这个等腰三角形的顶角为50°或80°.
6.B ∵等边三角形ABC的周长为a,∴AB=a∵BD⊥BC,AD⊥BD,∴∠ABD=30°,
∴AD=AB=a.
7.A 如图,要使△OAB为等腰三角形,应分三种情况讨论:①当OB=AB时,作线段OA的垂直平分线,与直线b的交点为B1;②当OA=AB时,以点A为圆心,OA的长为半径作圆,与直线b交于点B2;③当OA=OB时,以点O为圆心,OA的长为半径作圆,与直线b交于点B3,B4.故选A.
8.C ∵AB=AC,∠A=36°,∴∠ABC=∠C=72°.由作图痕迹可知BD平分∠ABC,∴∠DBC=∠ABD=∠A=36°,∴AD=BD,∠BDC=72°.故A,B选项不符合题意.由以上可知∠C=∠BDC,∴BD=BC,∴AD=BC.∵S△ABD∶S△BCD=AD∶CD∴S△ABD∶S△BCD=BC∶CD.故C选项符合题意.∵BD=AD,∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC=AB+BC.故D选项不符合题意.
9.C 如图,过点P作PC⊥OB于点C,∵∠AOB=60°,∴∠OPC=90°-∠AOB=30°.
∵OP=22,∴OC=OP=11.∵PM=PN,MN=4,∴MC=MN=2,∴OM=OC-MC=11-2=9.
10.B (转化思想)如图,作点D关于AB的对称点G,作点D关于BC的对称点H,连接GH交AB于点E,交BC于点F,此时△DEF的周长取得最小值,连接GB,BH.由线段垂直平分线的性质可得GE=ED,DF=FH,由轴对称的性质得BG=BD,BD=BH,∴ED+DF+EF=
GE+EF+FH=GH,此时△DEF的周长取得最小值GH.∵∠GBA=∠ABD,∠DBC=∠CBH,
∴∠GBH=2∠ABC=2×30°=60°,又BG=BH,∴△GBH是等边三角形∴GH=BG=BD=m,
∴△DEF的周长的最小值为m.
11.4 ∵∠C=90°,∠A=60°,∴∠B=90°-∠A=30°.∵AB=8,∴AC=AB=4.
12.垂直平分 ∵EH=FH,∴点H在EF的垂直平分线上.∵ED=FD,点D在EF的垂直平分线上,∴DH垂直平分EF.
13.先将△OCD关于y轴对称,再向上平移3个单位长度得到△AOB(答案不唯一)
14.20 ∵等腰三角形的两条边长分别为4 cm和8 cm,∴应分为两种情况:①8为底,4为腰,则4+4=8,此时不能构成三角形;②4为底,8为腰,则8+8+4=20(cm),∴它的
周长是20 cm.
15.(-a,b) 第1次变换后,点A在第四象限;第2次变换后,点A在第三象限;第3次变换后,点A在第二象限;第4次变换后,点A在第一象限,回到原始位置,…,以此类推,每4次变换为一组循环.因为2 023÷4=505……3,所以第2 023次变换后,点A在第二象限,坐标为(-a,b).
16.(1)2 (2)或 (1)∵∠C=90°,∠A=30°,AB=8 cm,∴∠B=60°,∴当PB=BQ时,△PBQ是等边三角形.由题意得AP=2t cm,BQ=t cm,∴BP=AB-AP=(6-2t)cm,
∴6-2t=t,解得t=2,∴当t=2时,△PBQ为等边三角形.(2)∵∠C=90°,∠A=30°,
∴∠B=60°,∴当△PBQ为直角三角形时,只能是∠PQB=90°或∠BPQ=90°.当∠PQB=90°时,如图(1),∴∠BPQ=30°,∴BQ=BP.∵BP=(6-2t)cm,BQ=t m,∴t=(6-2t),
解得t=.当∠BPQ=90°时,如图(2),∴∠PQB=30°,∴BQ=2BP,∴t=2(6-2t),解得t=.综上所述,当t=或t=时,△PBQ为直角三角形.
图(1) 图(2)
17.【参考答案】证明:连接AE,如图,
∵AB=AC,∠A=120°,∴∠B=∠C=30°.
∵DE垂直平分AB,∴BE=AE,
∴∠BAE=∠B=30°,
∴∠EAC=120°-30°=90°. (3分)
∵∠C=30°,
∴CE=2AE.
∵BE=AE,
∴CE=2BE. (6分)
18.【参考答案】(答案不唯一)如图所示. (8分)
(任选4个即可,每画对一个方案得2分)
19.【参考答案】该直升机继续向机场N飞行无危险. (1分)
理由:如图,过点C作CD⊥AN于点D,
∵∠NAC=15°, ∠NBC=30°,∴∠ACB=15°,CD=BC,
∴∠ACB=∠NAC,
∴BC=AB. (5分)
由题意可得AB=200 km,
∴BC=200 km,∴CD=100 km.
∵100>80,
∴该直升机继续向机场N飞行无危险. (8分)
20.【参考答案】(1)证明:如图,连接AD,
∵AB=AC,D是BC的中点,
∴AD平分∠BAC. (2分)
∵DE⊥AB,DF⊥AC,∴DE=DF,
∴△DEF是等腰三角形. (5分)
(2)120° (8分)
解法提示:∵∠AED=∠AFD=90°,
∴∠A+∠EDF=180°.
∵△DEF是等腰三角形,
∴当∠EDF=60°,△DEF为等边三角形,
此时∠A=120°.
21.【参考答案】【问题】∵AB=BD,∠B=30°,
∴∠BAD=∠ADB==75°.
∵∠BAF=90°,∴∠AFB=90°-30°=60°.
∵EF垂直平分AC,∴AF=CF,
∴∠CAF=∠C.
∵∠AFB=∠C+∠CAF=2∠C,
∴∠C=∠CAF=∠AFB=30°,
∴∠DAC=∠ADB-∠C=75°-30°=45°. (5分)
【探究】不变. (6分)
理由:∵AB=BD,
∴∠BAD=∠ADB==90°-∠B.
∵∠BAF=90°,∴∠AFB=90°-∠B.
∵EF垂直平分AC,∴AF=CF,
∴∠CAF=∠C.
∵∠AFB=∠C+∠CAF=2∠C,
∴∠C=∠CAF=∠AFB=45°-∠B,
∴∠DAC=∠ADB-∠C=90°-∠B-(45°-∠B)=45°. (10分)
22.【参考答案】(1)如图(1),△ABC为所作.
图(1) (3分)
(2)DP 到线段两端点的距离相等的点在线段的垂直平分线上 (7分)
(3)BC=AB. (9分)
证明:以点C为圆心,CB为半径画弧交AB于点D,连接CD,如图(2),则CD=CB.
图(2)
∵∠ACB=90°,∠A=30°,
∴∠B=60°.
∵CB=CD,
∴△CBD为等边三角形,
∴BD=CD=BC,∠BCD=60°.
∵∠ACD=∠ACB-∠BCD=30°,∴∠A=∠ACD,
∴AD=CD,
∴AD=BD=BC,∴BC=AB. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
2025人教版数学八年级上学期
第十三章 轴对称
时间 60分钟 满分 100分
一、选择题(共10小题,每小题3分,共30分.每小题有四个选项,其中只有一个选项符合题意)
1.(2023·北京燕山区期末)在数学活动课中,同学们利用几何画板绘制出了下列曲线,其中不是轴对称图形的是 ( )
A.等角螺旋线 B.心形线 C.四叶玫瑰线 D.蝴蝶曲线
2.(2023·山东菏泽定陶区期中)已知点P(2,a)与Q(2,b)关于x轴对称,则a+b= ( )
A.1 B.0 C.4 D.2
3.(2023·山东聊城期末)甲、乙、丙三地如图所示,若想建立一个货物中转仓,使其到甲、乙、丙三地的距离相等,则中转仓的位置应选在 ( )
A.三条角平分线的交点处 B.三边垂直平分线的交点处
C.三边中线的交点处 D.三边上的高的交点处
第3题 第4题 第6题
4.(2023·山西晋中期中)如图,一个小孩坐在秋千上,若秋千绕点O旋转了86°,小孩的位置也从A点运动到了A'点,则∠OA'A的度数为 ( )
A.33° B.37° C.43° D.47°
5.(2023·浙江宁波海曙区期末)已知等腰三角形的一个内角为50°,则它的顶角为 ( )
A.50° B.80° C.65°或80° D.50°或80°
6.(2023·河南潢川期末)如图,已知等边三角形ABC的周长为a,BD⊥BC,AD⊥BD,则AD等于 ( )
A.a B.a C.a D.
7.如图,直线a,b相交形成的角中,锐角为52°,交点为O,点A在直线a上,直线b上存在点B,使以点O,A,B为顶点的三角形是等腰三角形,这样的点B有 ( )
A.4个 B.3个 C.2个 D.1个
第7题 第8题
8.(2022·广东广州天河区期末)在△ABC中,AB=AC,∠A=36°,若按如图所示的尺规作图方法作出线段BD,则下列结论错误的是 ( )
A.AD=BD B.∠BDC=72°
C.S△ABD∶S△BCD=BC∶AC D.△BCD的周长=AB+BC
9.(2023·河北唐山十二中期末)如图,∠AOB=60°,点P在射线OA上,OP=22,点M,N在射线OB上(点M在点N的左侧),且PM=PN.若MN=4,则OM的长为 ( )
A.7 B.8 C.9 D.11
第9题 第10题
10.(2023·辽宁大连金普新区期末)如图,∠ABC=30°,点D是∠ABC内部的一点,连接BD.若BD=1m,点E,F分别是BA,BC上的动点,则△DEF的周长的最小值为 ( )
A.0.5m B.1m C.1.5m D.2m
二、填空题(本大题共6小题,每小题3分,共18分)
11.(2023·北京燕山区期末)已知Rt△ABC中,∠C=90°,∠A=60°,AB=8,则
AC= .
12.(2023·广西南宁期中)小军做了一个如图所示的风筝,其中EH=FH,ED=FD,则DH是EF的 线.
第12题 第13题
13.(2023·北京燕山区期中)如图,在平面直角坐标系xOy中,△AOB是由△OCD经过若干次的图形变化(平移、轴对称)得到的,请写出一种由△OCD得到△AOB的过程: .
14.(2023·广州八十九中期末)等腰三角形的两条边长分别为8 cm和4 cm,则它的周长是 cm.
15.(2022·河南济源期末)在平面直角坐标系中,对△ABC进行如图所示的轴对称变换.若原来点A的坐标是(a,b),则经过第2 023次变换后,点A所对应的坐标
是 .
16.(2023·石家庄新华区期末)如图,在△ABC中,∠C=90°,∠A=30°,AB=6 cm,动点P,Q同时从A,B两点出发,分别在AB,BC边上匀速移动,它们的速度分别为vP=2 cm/s,
vQ=1 cm/s,当点P到达点B时,P,Q两点同时停止运动,设点P的运动时间为t s.
①当t= 时,△PBQ为等边三角形;
②当t= 时,△PBQ为直角三角形.
选择题、填空题答题区
题号 1 2 3 4 5 6 7 8 9 10
答案
填空 11. 12. 13.
14. 15. 16.① ②
三、解答题(共6小题,共52分)
17.(6分)(2023·河南漯河郾城区期中)如图,在△ABC中,AB=AC,∠A=120°,DE垂直平分AB于D,交BC于E点,求证:CE=2BE.
18.(8分)(2023·北京通州区期末)如图是4×4正方形网格,其中有两个小正方形是涂黑的,请再选择三个小正方形并涂黑,使整个涂成黑色的图形为轴对称图形.请补全图形,并且画出对称轴(如图例),要求所画的四种方案不能重复.
19.(8分)(2022·湖北十堰郧阳区期中改编)某市发生地震后,为了抢救伤员,一架救援直升机从该市A地起飞,运送一批地震伤员沿正北方向到机场N,如图.上午8时,直升机从A地出发,以200 km/h的速度向正北方向飞行,9时到达B地,此时,机场的导航站传来信息:在C处有一座高山,因受天气影响,高山周围80 km内能见度低,飞行时会遇到危险.经测量得∠NAC=15°,∠NBC=30°.问该直升机继续向机场N飞行是否有危险,请说明理由.
20.(8分)(2023·北京二十中月考)如图,在△ABC中,AB=AC,D是BC的中点,DE⊥AB,
DF⊥AC,点E,F分别为垂足.
(1)求证:△DEF是等腰三角形.
(2)当∠A的度数为 时,△DEF是等边三角形.
21.(10分)(2022·河北石家庄裕华区期末)
【问题】
如图,在△ABC中,点D为BC边上一点,BD=BA.EF垂直平分AC,交AC于点E,交BC于点F,连接AD,AF.若∠B=30°,∠BAF=90°,求∠DAC的度数.
【探究】
如果把【问题】中的条件“∠B=30°”去掉,其他条件不变,那么∠DAC的度数会变吗 请说明理由.
22.(12分)(2023·安徽合肥蜀山区期末)下面是“已知斜边作一个直角三角形”的尺规作图过程.
已知:线段AB.
求作:一个直角三角形ABC,使线段AB为斜边.
作法:①过点A任意作一条射线l;
②在射线l上任取两点D,E;
③分别以点D,E为圆心,DB,EB长为半径作弧,两弧相交于点P;
④作射线BP交射线l于点C.
则△ABC就是所求作的直角三角形.
(1)使用直尺和圆规,在图(1)中依作法补全图形(保留作图痕迹).
(2)证明:连接DP,EP,
∵DB= ,
∴点D在线段BP的垂直平分线上.( )(填推理的依据)
同理可证,点E在线段BP的垂直平分线上.
根据两点确定一条直线,可知DE是线段BP的垂直平分线.
∴∠ACB=90°.
(3)如图(2),在Rt△ABC中,∠ACB=90°,∠A=30°.
猜想BC与AB满足的数量关系,并证明.
图(1) 图(2)
第十三章 轴对称
选择题、填空题答案速查
1 2 3 4 5 6 7 8 9 10
A B B D D B A C C B
11.4 12.垂直平分 13.先将△OCD关于y轴对称,再向上平移3个单位长度得到△AOB(答案不唯一)
14.20 15.(-a,b) 16.(1)2 (2)或
1.A
2.B ∵点P(2,a)与Q(2,b)关于x轴对称,∴a+b=0.
3.B 【点拨】线段的垂直平分线上的点到线段的两个端点的距离相等
4.D ∵秋千绕点O旋转了86°,小孩的位置也从A点运动到了A'点,∴∠AOA'=
86°,OA=OA',∴∠OA'A=×(180°-86°)=47°.
5.D 在△ABC中,AB=AC.分两种情况:①顶角∠A=50°.②当底角是50°时,
∵AB=AC,∴∠B=∠C=50°.∵∠A+∠B+∠C=180°,∴∠A=180°-50°-50°=80°.∴这个等腰三角形的顶角为50°或80°.
6.B ∵等边三角形ABC的周长为a,∴AB=a∵BD⊥BC,AD⊥BD,∴∠ABD=30°,
∴AD=AB=a.
7.A 如图,要使△OAB为等腰三角形,应分三种情况讨论:①当OB=AB时,作线段OA的垂直平分线,与直线b的交点为B1;②当OA=AB时,以点A为圆心,OA的长为半径作圆,与直线b交于点B2;③当OA=OB时,以点O为圆心,OA的长为半径作圆,与直线b交于点B3,B4.故选A.
8.C ∵AB=AC,∠A=36°,∴∠ABC=∠C=72°.由作图痕迹可知BD平分∠ABC,∴∠DBC=∠ABD=∠A=36°,∴AD=BD,∠BDC=72°.故A,B选项不符合题意.由以上可知∠C=∠BDC,∴BD=BC,∴AD=BC.∵S△ABD∶S△BCD=AD∶CD∴S△ABD∶S△BCD=BC∶CD.故C选项符合题意.∵BD=AD,∴△BCD的周长=BC+CD+BD=BC+CD+AD=BC+AC=AB+BC.故D选项不符合题意.
9.C 如图,过点P作PC⊥OB于点C,∵∠AOB=60°,∴∠OPC=90°-∠AOB=30°.
∵OP=22,∴OC=OP=11.∵PM=PN,MN=4,∴MC=MN=2,∴OM=OC-MC=11-2=9.
10.B (转化思想)如图,作点D关于AB的对称点G,作点D关于BC的对称点H,连接GH交AB于点E,交BC于点F,此时△DEF的周长取得最小值,连接GB,BH.由线段垂直平分线的性质可得GE=ED,DF=FH,由轴对称的性质得BG=BD,BD=BH,∴ED+DF+EF=
GE+EF+FH=GH,此时△DEF的周长取得最小值GH.∵∠GBA=∠ABD,∠DBC=∠CBH,
∴∠GBH=2∠ABC=2×30°=60°,又BG=BH,∴△GBH是等边三角形∴GH=BG=BD=m,
∴△DEF的周长的最小值为m.
11.4 ∵∠C=90°,∠A=60°,∴∠B=90°-∠A=30°.∵AB=8,∴AC=AB=4.
12.垂直平分 ∵EH=FH,∴点H在EF的垂直平分线上.∵ED=FD,点D在EF的垂直平分线上,∴DH垂直平分EF.
13.先将△OCD关于y轴对称,再向上平移3个单位长度得到△AOB(答案不唯一)
14.20 ∵等腰三角形的两条边长分别为4 cm和8 cm,∴应分为两种情况:①8为底,4为腰,则4+4=8,此时不能构成三角形;②4为底,8为腰,则8+8+4=20(cm),∴它的
周长是20 cm.
15.(-a,b) 第1次变换后,点A在第四象限;第2次变换后,点A在第三象限;第3次变换后,点A在第二象限;第4次变换后,点A在第一象限,回到原始位置,…,以此类推,每4次变换为一组循环.因为2 023÷4=505……3,所以第2 023次变换后,点A在第二象限,坐标为(-a,b).
16.(1)2 (2)或 (1)∵∠C=90°,∠A=30°,AB=8 cm,∴∠B=60°,∴当PB=BQ时,△PBQ是等边三角形.由题意得AP=2t cm,BQ=t cm,∴BP=AB-AP=(6-2t)cm,
∴6-2t=t,解得t=2,∴当t=2时,△PBQ为等边三角形.(2)∵∠C=90°,∠A=30°,
∴∠B=60°,∴当△PBQ为直角三角形时,只能是∠PQB=90°或∠BPQ=90°.当∠PQB=90°时,如图(1),∴∠BPQ=30°,∴BQ=BP.∵BP=(6-2t)cm,BQ=t m,∴t=(6-2t),
解得t=.当∠BPQ=90°时,如图(2),∴∠PQB=30°,∴BQ=2BP,∴t=2(6-2t),解得t=.综上所述,当t=或t=时,△PBQ为直角三角形.
图(1) 图(2)
17.【参考答案】证明:连接AE,如图,
∵AB=AC,∠A=120°,∴∠B=∠C=30°.
∵DE垂直平分AB,∴BE=AE,
∴∠BAE=∠B=30°,
∴∠EAC=120°-30°=90°. (3分)
∵∠C=30°,
∴CE=2AE.
∵BE=AE,
∴CE=2BE. (6分)
18.【参考答案】(答案不唯一)如图所示. (8分)
(任选4个即可,每画对一个方案得2分)
19.【参考答案】该直升机继续向机场N飞行无危险. (1分)
理由:如图,过点C作CD⊥AN于点D,
∵∠NAC=15°, ∠NBC=30°,∴∠ACB=15°,CD=BC,
∴∠ACB=∠NAC,
∴BC=AB. (5分)
由题意可得AB=200 km,
∴BC=200 km,∴CD=100 km.
∵100>80,
∴该直升机继续向机场N飞行无危险. (8分)
20.【参考答案】(1)证明:如图,连接AD,
∵AB=AC,D是BC的中点,
∴AD平分∠BAC. (2分)
∵DE⊥AB,DF⊥AC,∴DE=DF,
∴△DEF是等腰三角形. (5分)
(2)120° (8分)
解法提示:∵∠AED=∠AFD=90°,
∴∠A+∠EDF=180°.
∵△DEF是等腰三角形,
∴当∠EDF=60°,△DEF为等边三角形,
此时∠A=120°.
21.【参考答案】【问题】∵AB=BD,∠B=30°,
∴∠BAD=∠ADB==75°.
∵∠BAF=90°,∴∠AFB=90°-30°=60°.
∵EF垂直平分AC,∴AF=CF,
∴∠CAF=∠C.
∵∠AFB=∠C+∠CAF=2∠C,
∴∠C=∠CAF=∠AFB=30°,
∴∠DAC=∠ADB-∠C=75°-30°=45°. (5分)
【探究】不变. (6分)
理由:∵AB=BD,
∴∠BAD=∠ADB==90°-∠B.
∵∠BAF=90°,∴∠AFB=90°-∠B.
∵EF垂直平分AC,∴AF=CF,
∴∠CAF=∠C.
∵∠AFB=∠C+∠CAF=2∠C,
∴∠C=∠CAF=∠AFB=45°-∠B,
∴∠DAC=∠ADB-∠C=90°-∠B-(45°-∠B)=45°. (10分)
22.【参考答案】(1)如图(1),△ABC为所作.
图(1) (3分)
(2)DP 到线段两端点的距离相等的点在线段的垂直平分线上 (7分)
(3)BC=AB. (9分)
证明:以点C为圆心,CB为半径画弧交AB于点D,连接CD,如图(2),则CD=CB.
图(2)
∵∠ACB=90°,∠A=30°,
∴∠B=60°.
∵CB=CD,
∴△CBD为等边三角形,
∴BD=CD=BC,∠BCD=60°.
∵∠ACD=∠ACB-∠BCD=30°,∴∠A=∠ACD,
∴AD=CD,
∴AD=BD=BC,∴BC=AB. (12分)
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
