六年级下册数学人教版圆柱与圆锥课件(共21张PPT)
文档属性
| 名称 | 六年级下册数学人教版圆柱与圆锥课件(共21张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 377.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-11 15:48:20 | ||
图片预览



文档简介
(共21张PPT)
第二讲:圆柱与圆锥巩固
1、圆柱侧面积、表面积应用
2、圆柱体积应用
3、几何体切割
4、等体积变形
本讲聚焦
一.例题精讲
【圆柱基本概念】
立体图形 表面积
体积
圆柱
Ch=2πrh
=πdh
πr2
Sh = πr2h=
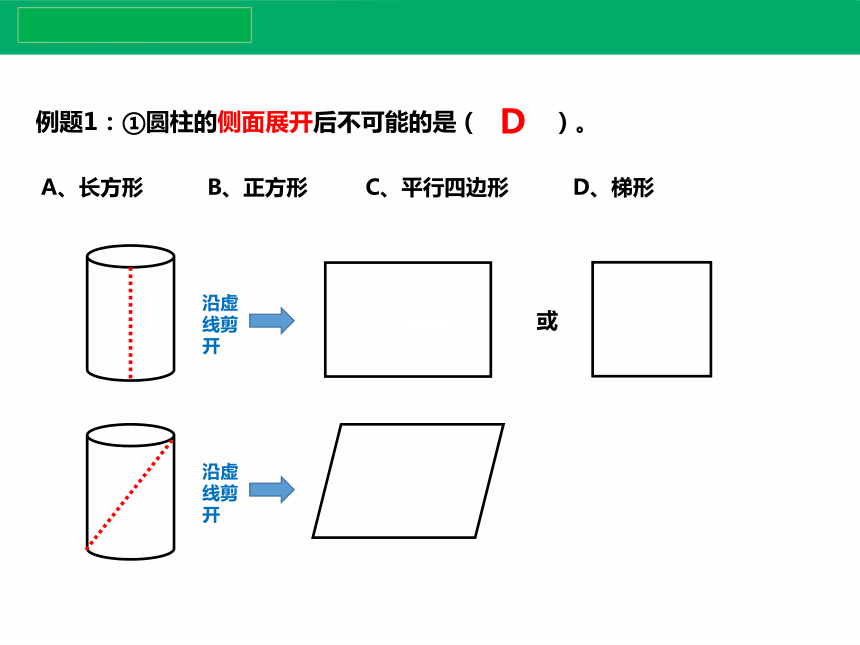
例题1:①圆柱的侧面展开后不可能的是( )。
D
沿虚线剪开
或
沿虚线剪开
A、长方形 B、正方形 C、平行四边形 D、梯形
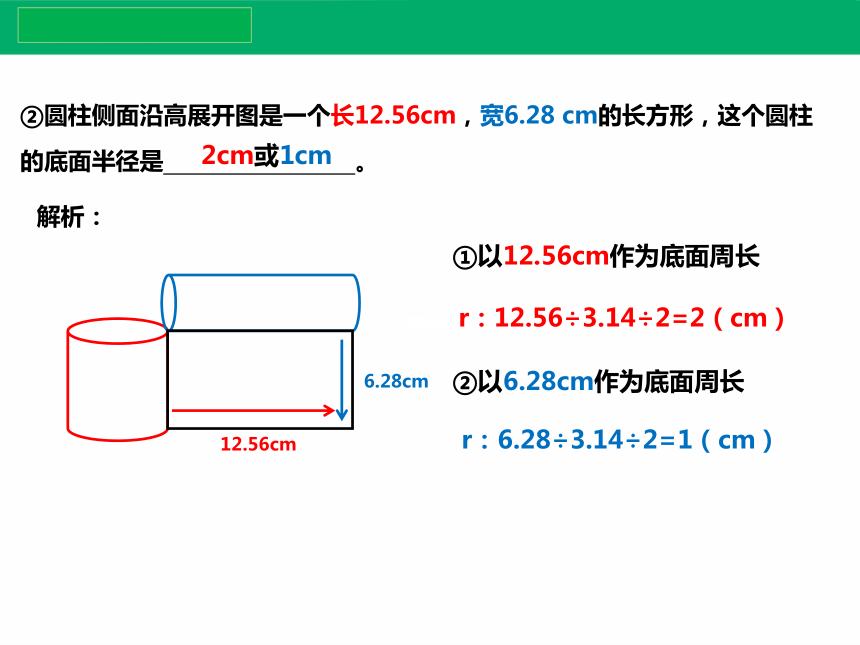
②圆柱侧面沿高展开图是一个长12.56cm,宽6.28 cm的长方形,这个圆柱的底面半径是 。
①以12.56cm作为底面周长
r:6.28÷3.14÷2=1(cm)
②以6.28cm作为底面周长
r:12.56÷3.14÷2=2(cm)
2cm或1cm
12.56cm
6.28cm
解析:
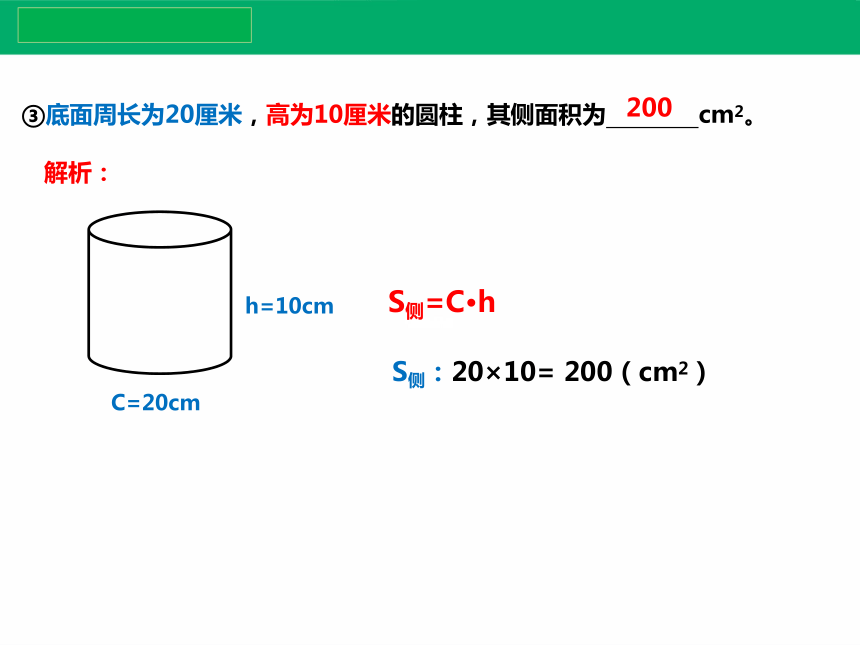
③底面周长为20厘米,高为10厘米的圆柱,其侧面积为 cm2。
C=20cm
h=10cm
S侧:20×10= 200(cm2)
200
S侧=C·h
解析:
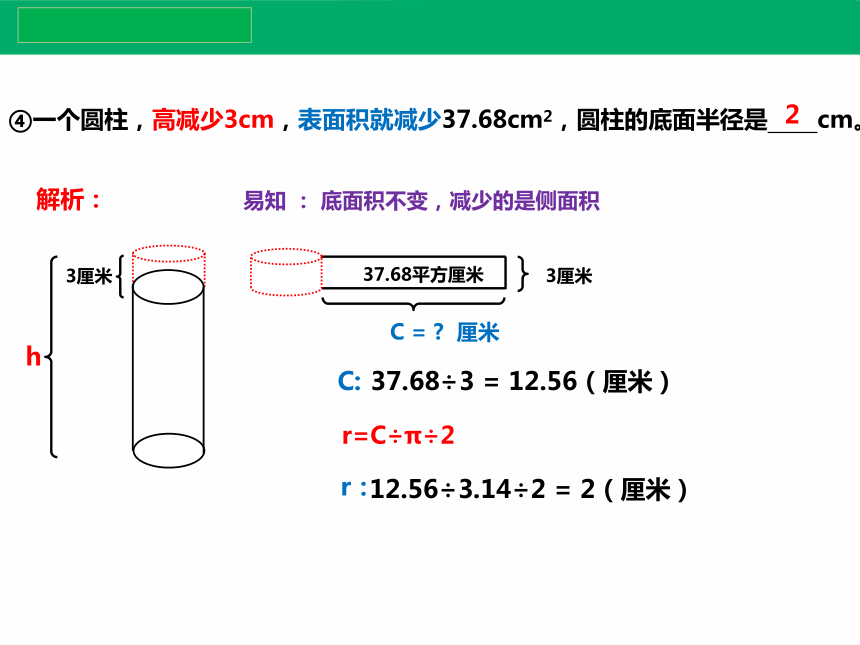
④一个圆柱,高减少3cm,表面积就减少37.68cm2,圆柱的底面半径是 cm。
3厘米
h
易知 : 底面积不变,减少的是侧面积
12.56÷3.14÷2 = 2(厘米)
2
37.68平方厘米
3厘米
C = 厘米
C:
37.68÷3 = 12.56(厘米)
r:
r=C÷π÷2
解析:
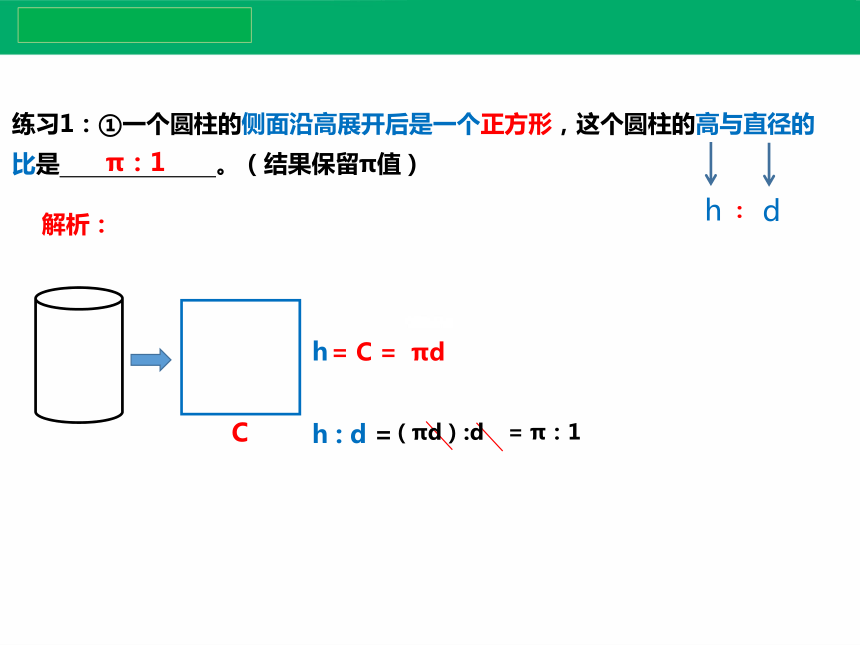
练习1:①一个圆柱的侧面沿高展开后是一个正方形,这个圆柱的高与直径的比是 。(结果保留π值)
C
h
h : d =
π:1
= C = πd
h
d
:
(πd):d
= π:1
解析:
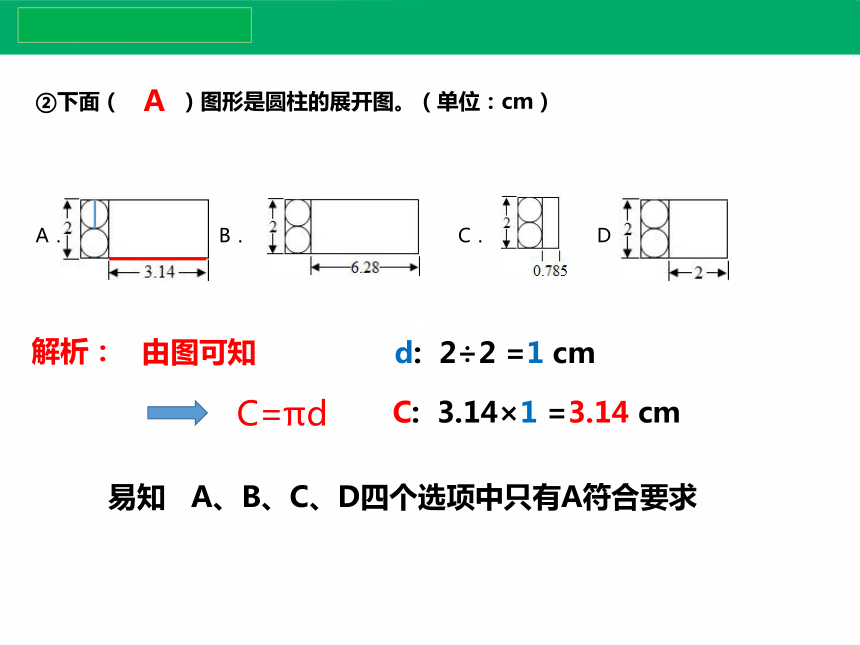
②下面( )图形是圆柱的展开图。(单位:cm)
A. B. C. D.
易知 A、B、C、D四个选项中只有A符合要求
由图可知
A
d: 2÷2 =1 cm
C: 3.14×1 =3.14 cm
C=πd
解析:
③一个圆柱高8cm,如果高增加2cm,它的表面积就增加37.68cm2,则原来圆柱的侧面积是 cm2。
37.68平方厘米
2厘米
8厘米
C:37.68÷2=18.84(cm2)
S侧:18.84×8=150.72(cm2)
C
h=2
S侧 = Ch
150.72
【圆柱体积公式推导】
例题2:①把圆柱的底面分成许多相等的扇形,然后把圆柱切开,拼成近似的长方体,这个长方体的底面积等于圆柱( ),长方体的高就是( )的高,因为长方体的体积等于底面积乘高,所以圆柱体的体积就( ),用字母表示为( )。
底面积
圆柱
底面积×高
V柱=S h
②如图所示,把底面周长18.84cm、高10cm的圆柱切成若干等分,拼成一个近似长方体。这个长方体的长、宽、高、体积各是多少?
V柱=πr2h V柱:3.14×3×3×10=282.6 (cm2)
V长 = V柱 = 282.6(cm3)
底面半径
圆柱的高
圆柱底面周长÷2
r: 18.84÷3.14÷2=3 (cm)
长方形的长=圆柱底面周长÷2
18.84÷2=9.42(cm)
r=c÷π÷2
长方形的宽=圆柱底面半径
h=10cm
长方形的高=圆柱的高
练习2:①把一个底面半径为3dm的圆柱底面平均分成若干个扇形,截开拼成一个与它等底等高的近似长方体后,表面积增加16dm2。求圆柱的体积。
增加左右2个长方形
S长:16÷2=8(dm2)
h=
8
8
V柱 = Sh=πr2h
r=3
h
r
+
= 16
h: 8÷3= (dm)
V柱:3.14×3×3× =75.36(dm3)
练习2:②圆柱体的侧面积是80平方分米,底面半径是3分米,它的体积是多少?
r
V柱:(80÷2)×3=120(dm3)
翻倒
以侧面积的一半为底面积,
以半径为高
V柱: S底 h
= S侧 r
【几何体切割】
例题3:①一根圆柱形木料,底面直径是2分米,高是5分米,如果沿底面直径切成完全相同的两块,其中一块的表面积是多少平方分米?
d=2dm
h=5dm
S侧÷2
S底:3.14×1×1=3.14(dm2)
r: 2÷2=1 (dm)
S侧:3.14×2×5=31.4(dm2)
S长:2×5=10(dm2)
S表:3.14+10+31.4÷2=28.84(dm2)
S表 =
S底 +
S长+
S底=πr2
S侧=Ch=πdh
例题3:②把一个高为4厘米圆柱沿直径切开,平均分成两部分,表面积就增加16平方厘米,求原来圆柱的体积。
S长:16÷2=8(cm2)
r: 2÷2=1(cm)
V柱:3.14×1×1×4=12.56(cm3)
增加两个长方形的面积
+
= 16
V柱 = Sh=πr2h
8
8
h=4
d=?
d=2
d:8÷4=2(cm)
练习3:①一段圆柱体木料,如果截成两个小圆柱体,它的表面积增加12.56平方厘米;如果沿着底面直径截成两个半圆柱体,那么它的表面积将增加80平方厘米,求原来圆柱体的表面积。
+
= 80
40
40
h
d
+
=12.56
S圆:12.56÷2=6.28(cm2)
S侧=Πdh
S长=dh S长:80÷2=40(cm2)
S侧:3.14×40=125.6(cm2)
S表:6.28×2+125.6=138.16(cm2)
整体代入
练习3:②将一根长5米的圆柱形木料锯成4段后,截成的4小段表面积之和比原来圆柱增加60cm2,这根木料体积是多少立方厘米?
截成的4小段,表面积之和比原来圆柱增加
6个圆底面
S圆:60÷6=10(cm2)
5m=500cm
V柱:10×500=5000(cm3)
=
解:设能铺 x 米长的路面。
=
10×0.02 x
20 = 0.2x
100 = x
【等积变形】
例题4:一个圆锥形沙堆,底面积是24平方米,高是2.5米,用这堆沙子在10米宽的路上铺2厘米厚的路面,能铺多少米?
方法一:
等量关系式:V锥 = V长
x = 100
方法二:
2厘米=0.02米
V长 = V锥 =20(立方米)
长=V长÷宽÷高
长:20÷10÷0.02=100(米)
2 厘米 = 0.02 米
×24×2.5
V锥= Sh
V锥: ×24×2.5=20(立方米)
练习4:①把一块长6dm,宽5dm,高2dm的长方体铁块,熔铸成一个高为4dm的圆柱体铁饼,求这铁饼的底面积。
=
解:设这铁饼的底面积为xdm2。
=
4 x
60 = 4x
15 = x
方法一:
等量关系式:V长 = V圆柱
x = 15
方法二:
V长 = V圆柱
底面积:60÷4=15(平方米)
6×5×2
V长= 长×宽×高
V长: 6×5×2=60(立方米)
练习4:②把一个长、宽、高分别是10cm、6.3cm、3cm的长方体铁块和一个棱长为5cm的正方体铁块,熔铸成一个底面半径为5cm的圆锥体铁块。求这个圆锥的高。
=
解:设这个圆锥的高为xcm。
=
方法一:
等量关系式:V长 + V正 = V圆锥
x = 12
方法二:
V长+正 = V圆锥
10×6.3×3+5×5×5
V长+正:
10×6.3×3+5×5×5=314(立方厘米)
+
×3.14×5×5×x
314 =
×3.14×25×x
3.14×100 =
×3.14×25×x
100 =
×25×x
高:314÷ ÷(3.14×5×5) =12(厘米)
V圆锥= Sh
h=V圆锥÷ ÷S
第二讲:圆柱与圆锥巩固
1、圆柱侧面积、表面积应用
2、圆柱体积应用
3、几何体切割
4、等体积变形
本讲聚焦
一.例题精讲
【圆柱基本概念】
立体图形 表面积
体积
圆柱
Ch=2πrh
=πdh
πr2
Sh = πr2h=
例题1:①圆柱的侧面展开后不可能的是( )。
D
沿虚线剪开
或
沿虚线剪开
A、长方形 B、正方形 C、平行四边形 D、梯形
②圆柱侧面沿高展开图是一个长12.56cm,宽6.28 cm的长方形,这个圆柱的底面半径是 。
①以12.56cm作为底面周长
r:6.28÷3.14÷2=1(cm)
②以6.28cm作为底面周长
r:12.56÷3.14÷2=2(cm)
2cm或1cm
12.56cm
6.28cm
解析:
③底面周长为20厘米,高为10厘米的圆柱,其侧面积为 cm2。
C=20cm
h=10cm
S侧:20×10= 200(cm2)
200
S侧=C·h
解析:
④一个圆柱,高减少3cm,表面积就减少37.68cm2,圆柱的底面半径是 cm。
3厘米
h
易知 : 底面积不变,减少的是侧面积
12.56÷3.14÷2 = 2(厘米)
2
37.68平方厘米
3厘米
C = 厘米
C:
37.68÷3 = 12.56(厘米)
r:
r=C÷π÷2
解析:
练习1:①一个圆柱的侧面沿高展开后是一个正方形,这个圆柱的高与直径的比是 。(结果保留π值)
C
h
h : d =
π:1
= C = πd
h
d
:
(πd):d
= π:1
解析:
②下面( )图形是圆柱的展开图。(单位:cm)
A. B. C. D.
易知 A、B、C、D四个选项中只有A符合要求
由图可知
A
d: 2÷2 =1 cm
C: 3.14×1 =3.14 cm
C=πd
解析:
③一个圆柱高8cm,如果高增加2cm,它的表面积就增加37.68cm2,则原来圆柱的侧面积是 cm2。
37.68平方厘米
2厘米
8厘米
C:37.68÷2=18.84(cm2)
S侧:18.84×8=150.72(cm2)
C
h=2
S侧 = Ch
150.72
【圆柱体积公式推导】
例题2:①把圆柱的底面分成许多相等的扇形,然后把圆柱切开,拼成近似的长方体,这个长方体的底面积等于圆柱( ),长方体的高就是( )的高,因为长方体的体积等于底面积乘高,所以圆柱体的体积就( ),用字母表示为( )。
底面积
圆柱
底面积×高
V柱=S h
②如图所示,把底面周长18.84cm、高10cm的圆柱切成若干等分,拼成一个近似长方体。这个长方体的长、宽、高、体积各是多少?
V柱=πr2h V柱:3.14×3×3×10=282.6 (cm2)
V长 = V柱 = 282.6(cm3)
底面半径
圆柱的高
圆柱底面周长÷2
r: 18.84÷3.14÷2=3 (cm)
长方形的长=圆柱底面周长÷2
18.84÷2=9.42(cm)
r=c÷π÷2
长方形的宽=圆柱底面半径
h=10cm
长方形的高=圆柱的高
练习2:①把一个底面半径为3dm的圆柱底面平均分成若干个扇形,截开拼成一个与它等底等高的近似长方体后,表面积增加16dm2。求圆柱的体积。
增加左右2个长方形
S长:16÷2=8(dm2)
h=
8
8
V柱 = Sh=πr2h
r=3
h
r
+
= 16
h: 8÷3= (dm)
V柱:3.14×3×3× =75.36(dm3)
练习2:②圆柱体的侧面积是80平方分米,底面半径是3分米,它的体积是多少?
r
V柱:(80÷2)×3=120(dm3)
翻倒
以侧面积的一半为底面积,
以半径为高
V柱: S底 h
= S侧 r
【几何体切割】
例题3:①一根圆柱形木料,底面直径是2分米,高是5分米,如果沿底面直径切成完全相同的两块,其中一块的表面积是多少平方分米?
d=2dm
h=5dm
S侧÷2
S底:3.14×1×1=3.14(dm2)
r: 2÷2=1 (dm)
S侧:3.14×2×5=31.4(dm2)
S长:2×5=10(dm2)
S表:3.14+10+31.4÷2=28.84(dm2)
S表 =
S底 +
S长+
S底=πr2
S侧=Ch=πdh
例题3:②把一个高为4厘米圆柱沿直径切开,平均分成两部分,表面积就增加16平方厘米,求原来圆柱的体积。
S长:16÷2=8(cm2)
r: 2÷2=1(cm)
V柱:3.14×1×1×4=12.56(cm3)
增加两个长方形的面积
+
= 16
V柱 = Sh=πr2h
8
8
h=4
d=?
d=2
d:8÷4=2(cm)
练习3:①一段圆柱体木料,如果截成两个小圆柱体,它的表面积增加12.56平方厘米;如果沿着底面直径截成两个半圆柱体,那么它的表面积将增加80平方厘米,求原来圆柱体的表面积。
+
= 80
40
40
h
d
+
=12.56
S圆:12.56÷2=6.28(cm2)
S侧=Πdh
S长=dh S长:80÷2=40(cm2)
S侧:3.14×40=125.6(cm2)
S表:6.28×2+125.6=138.16(cm2)
整体代入
练习3:②将一根长5米的圆柱形木料锯成4段后,截成的4小段表面积之和比原来圆柱增加60cm2,这根木料体积是多少立方厘米?
截成的4小段,表面积之和比原来圆柱增加
6个圆底面
S圆:60÷6=10(cm2)
5m=500cm
V柱:10×500=5000(cm3)
=
解:设能铺 x 米长的路面。
=
10×0.02 x
20 = 0.2x
100 = x
【等积变形】
例题4:一个圆锥形沙堆,底面积是24平方米,高是2.5米,用这堆沙子在10米宽的路上铺2厘米厚的路面,能铺多少米?
方法一:
等量关系式:V锥 = V长
x = 100
方法二:
2厘米=0.02米
V长 = V锥 =20(立方米)
长=V长÷宽÷高
长:20÷10÷0.02=100(米)
2 厘米 = 0.02 米
×24×2.5
V锥= Sh
V锥: ×24×2.5=20(立方米)
练习4:①把一块长6dm,宽5dm,高2dm的长方体铁块,熔铸成一个高为4dm的圆柱体铁饼,求这铁饼的底面积。
=
解:设这铁饼的底面积为xdm2。
=
4 x
60 = 4x
15 = x
方法一:
等量关系式:V长 = V圆柱
x = 15
方法二:
V长 = V圆柱
底面积:60÷4=15(平方米)
6×5×2
V长= 长×宽×高
V长: 6×5×2=60(立方米)
练习4:②把一个长、宽、高分别是10cm、6.3cm、3cm的长方体铁块和一个棱长为5cm的正方体铁块,熔铸成一个底面半径为5cm的圆锥体铁块。求这个圆锥的高。
=
解:设这个圆锥的高为xcm。
=
方法一:
等量关系式:V长 + V正 = V圆锥
x = 12
方法二:
V长+正 = V圆锥
10×6.3×3+5×5×5
V长+正:
10×6.3×3+5×5×5=314(立方厘米)
+
×3.14×5×5×x
314 =
×3.14×25×x
3.14×100 =
×3.14×25×x
100 =
×25×x
高:314÷ ÷(3.14×5×5) =12(厘米)
V圆锥= Sh
h=V圆锥÷ ÷S
