10.3.1 图形的旋转 课件(共16张PPT)(重庆市第九届初中数学青年教师优质课江津)
文档属性
| 名称 | 10.3.1 图形的旋转 课件(共16张PPT)(重庆市第九届初中数学青年教师优质课江津) |

|
|
| 格式 | pptx | ||
| 文件大小 | 31.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
数学之美
圆的极限Ⅲ
埃舍尔
非欧图示
克斯特
中国陶瓷
圆的极限Ⅲ
埃舍尔
非欧图示
克斯特
圆的极限Ⅲ
埃舍尔
非欧图示
克斯特
10.3.1图形的旋转
我们是如何研究平移的?
温故知新
生活中的平移现象
平移的概念
(影响平移的因素)
平移的特征
平移的应用
生活中的旋转现象无处不在
P
P′
O
A
P
B
C
D
A
A′
B′
D′
C′
A′
O
新知探究
旋转的概念
你能归纳、概括出上述运动过程的共同特点吗?
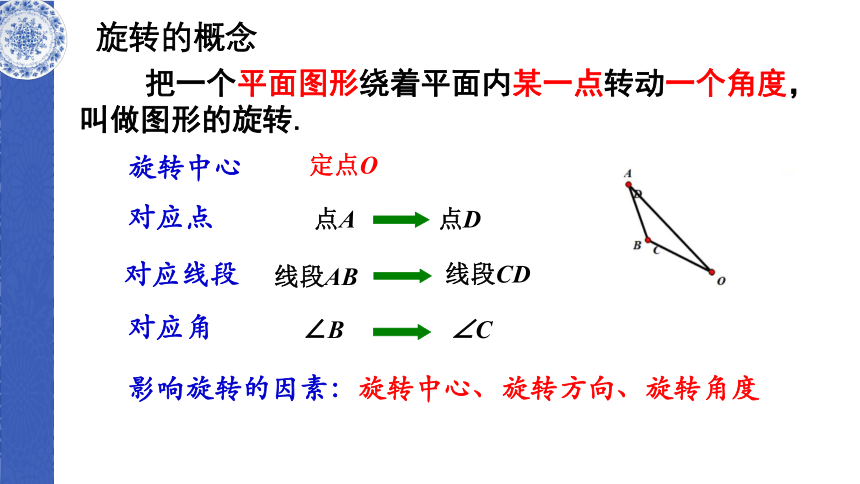
旋转的概念
把一个平面图形绕着平面内某一点转动一个角度,叫做图形的旋转.
点D
点A
线段CD
线段AB
∠B
对应点
对应线段
对应角
∠C
旋转中心
定点O
影响旋转的因素:旋转中心、旋转方向、旋转角度
探究与发现
在硬纸板上,挖一个三角形,硬纸板下面放一张白纸.
第一步:用圆规的针尖在硬纸板上扎一个小洞O作为旋转中心;
第二步:先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心O转动硬纸板(任意角度),再描出这个挖掉的三角形(△A'B'C' ),移开硬纸板.
问题:在旋转的过程中,你有什么发现?
发现:旋转不改变图形的形状和大小.
例1.△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.
(1)旋转中心是________;
点A
(2)线段AB的对应线段是_____,
∠B的对应角是________;
AC
∠ACE
(3)旋转了多少度?
60°
(4)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
线段AC中点
例2.如图①点M是线段AB上一点,
(1)将线段AB绕着点M顺时针旋转90°的图形是____,
旋转后的线段与原线段的位置关系是________;
(2)将线段AB绕着点M逆时针旋转90°的图形是____,
旋转后的线段与原线段的位置关系是________.
① ② ③
②
③
互相垂直
互相垂直
学生活动:利用旋转变换进行图案设计,并简要描述你的设计过程.
材料包工具:图形模具、圆盘面、马克笔、圆规等.
《我是陶瓷盘面设计师》
创意活动
总结与感悟
1.你学到了哪些知识?
2.你体会到哪些数学思想?
3.你学会了哪些研究问题的方法?
2.本节课你感受最深的是什么?
请你选择感兴趣的1—2个问题谈谈你的想法.
课堂小结
生活实例
平面图形
旋转的概念
旋转的影响因素
抽象
观察
归纳
探究
发现
课后作业
基础训练:教材121页练习2、3题;
课外拓展:旋转除了具有极高的美学价值以外,在机械工程、交通工具、家用电器、建筑业、体育运动、电子设备、教育与玩具等多方面有着广泛运用,查找资料,与大家一起分享.
数学之美
圆的极限Ⅲ
埃舍尔
非欧图示
克斯特
中国陶瓷
圆的极限Ⅲ
埃舍尔
非欧图示
克斯特
圆的极限Ⅲ
埃舍尔
非欧图示
克斯特
10.3.1图形的旋转
我们是如何研究平移的?
温故知新
生活中的平移现象
平移的概念
(影响平移的因素)
平移的特征
平移的应用
生活中的旋转现象无处不在
P
P′
O
A
P
B
C
D
A
A′
B′
D′
C′
A′
O
新知探究
旋转的概念
你能归纳、概括出上述运动过程的共同特点吗?
旋转的概念
把一个平面图形绕着平面内某一点转动一个角度,叫做图形的旋转.
点D
点A
线段CD
线段AB
∠B
对应点
对应线段
对应角
∠C
旋转中心
定点O
影响旋转的因素:旋转中心、旋转方向、旋转角度
探究与发现
在硬纸板上,挖一个三角形,硬纸板下面放一张白纸.
第一步:用圆规的针尖在硬纸板上扎一个小洞O作为旋转中心;
第二步:先在纸上描出这个挖掉的三角形图案(△ABC),然后围绕旋转中心O转动硬纸板(任意角度),再描出这个挖掉的三角形(△A'B'C' ),移开硬纸板.
问题:在旋转的过程中,你有什么发现?
发现:旋转不改变图形的形状和大小.
例1.△ABC是等边三角形,D是BC上一点,△ABD经过逆时针旋转后到达△ACE的位置.
(1)旋转中心是________;
点A
(2)线段AB的对应线段是_____,
∠B的对应角是________;
AC
∠ACE
(3)旋转了多少度?
60°
(4)如果M是AB的中点,那么经过上述旋转后,点M转到了什么位置?
线段AC中点
例2.如图①点M是线段AB上一点,
(1)将线段AB绕着点M顺时针旋转90°的图形是____,
旋转后的线段与原线段的位置关系是________;
(2)将线段AB绕着点M逆时针旋转90°的图形是____,
旋转后的线段与原线段的位置关系是________.
① ② ③
②
③
互相垂直
互相垂直
学生活动:利用旋转变换进行图案设计,并简要描述你的设计过程.
材料包工具:图形模具、圆盘面、马克笔、圆规等.
《我是陶瓷盘面设计师》
创意活动
总结与感悟
1.你学到了哪些知识?
2.你体会到哪些数学思想?
3.你学会了哪些研究问题的方法?
2.本节课你感受最深的是什么?
请你选择感兴趣的1—2个问题谈谈你的想法.
课堂小结
生活实例
平面图形
旋转的概念
旋转的影响因素
抽象
观察
归纳
探究
发现
课后作业
基础训练:教材121页练习2、3题;
课外拓展:旋转除了具有极高的美学价值以外,在机械工程、交通工具、家用电器、建筑业、体育运动、电子设备、教育与玩具等多方面有着广泛运用,查找资料,与大家一起分享.
