19.1.1 矩形的性质 课件(共21张PPT)(重庆市第九届初中数学青年教师优质课开州)
文档属性
| 名称 | 19.1.1 矩形的性质 课件(共21张PPT)(重庆市第九届初中数学青年教师优质课开州) |

|
|
| 格式 | pptx | ||
| 文件大小 | 11.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
Math
第19章 矩形、菱形与正方形
19.1.1 矩形的性质
创设情境,引入新课
生活中的矩形、菱形与正方形
第19章 矩形、菱形与正方形
类比旧知,探究新知
A
B
C
D
你对平行四边形有哪些方面的认识呢?
定义
性质
判定
矩形的探究路径
┐
A
B
C
D
师生互动,探究新知
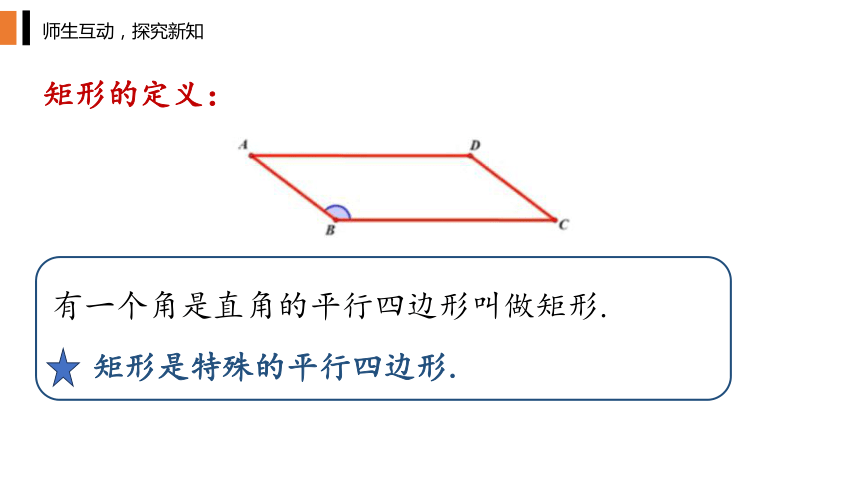
矩形是特殊的平行四边形.
有一个角是直角的平行四边形叫做矩形.
矩形的定义:
矩形的探究路径:
师生互动,探究新知
┐
A
B
C
D
有一个角是直角的平行四边形叫做矩形.
对称性:
边:
角:
对角线:
定义
性质
判定
A
B
C
D
┐
A
B
C
D
有一个角是直角
师生互动,探究新知
对称性
边
角
对角线
中心对称图形
轴对称图形
对边平行且相等
对角相等
邻角互补
四个角都是直角
邻边垂直
矩形的性质
平行四边形的
一般性质
对角线互相平分
矩形的特殊性质
O
对角线相等
┐
A
B
C
D
对称性
边
师生互动,探究新知
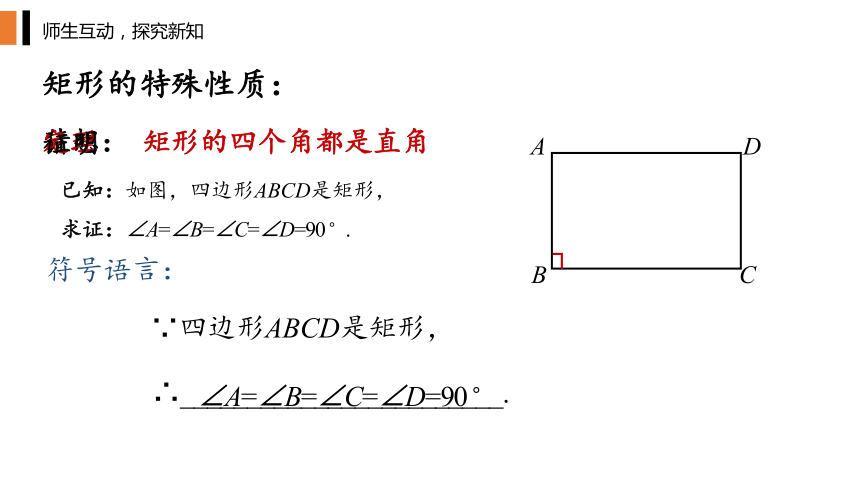
矩形的四个角都是直角
符号语言:
∵四边形ABCD是矩形,
∴________________________.
猜想:
定理
∠A=∠B=∠C=∠D=90
矩形的特殊性质:
证明
已知:如图,四边形ABCD是矩形,
求证:∠A=∠B=∠C=∠D=90 .
对称性
边
对角线
师生互动,探究新知
矩形的特殊性质:
矩形的对角线相等
符号语言:
∵______________________,
∴________________________.
猜想:
定理
AC=BD
四边形ABCD是矩形
┐
A
B
C
D
O
证明
已知:如图,四边形ABCD是矩形,
求证:AC=BD.
矩形的探究路径:
师生互动,探究新知
有一个角是直角的平行四边形叫做矩形.
对称性:
边:
角:
对角线:
定义
性质
判定
中心对称图形+轴对称图形
对边平行且相等
四个角都是直角
相等且互相平分
┐
A
B
C
D
O
应用知识,解决问题
练习1 如图,在矩形ABCD中对角线AC与BD相交于点O(1)若AB=6,BC=8,则AC=______,OB=_______.
5
10
6
(2)若AB=6,BC=8,求△ BOC与△ AOB的周长之差.
8
解题思路: BC- AB=2
A
B
C
D
边
例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长和是86 cm,矩形的对角线长是13 cm,那么该矩形的周长是多少?
应用知识,解决问题
O
应用知识,解决问题
练习2 如图,在矩形ABCD中对角线AC与BD相交于点O ,∠AOB=60° , AB=4,求对角线的长。
60°
4
解题指南:
当对角线的夹角为60 °或120 °时,利用等边三角形解决问题.
应用知识,解决问题
练习3 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
A.9cm B.8cm C.7cm D.6cm
B
4cm
5cm
1
2
3
边
课堂小结,交流评价
本节课你有哪些收获?
一个路径:
二个主要思想方法:
三个特殊性质:
“一二三”
1.轴对称图形;
2.四个角都是直角;
3.对角线相等.
定义 性质 判定
类比思想、猜想思想
应用
你的人生是旷野!
课后作业,提升巩固
必做题:教科书第100页,练习2、练习3;
选做题:如图,矩形ABCD沿着直线BD折叠,使点C落在C′处, BC′交AD于点E,已知AD=8,AB=4,求△BED的面积;
实践作业:请用矩形设计一个优美的图案.
课后作业
Math
第19章 矩形、菱形与正方形
19.1.1 矩形的性质
创设情境,引入新课
生活中的矩形、菱形与正方形
第19章 矩形、菱形与正方形
类比旧知,探究新知
A
B
C
D
你对平行四边形有哪些方面的认识呢?
定义
性质
判定
矩形的探究路径
┐
A
B
C
D
师生互动,探究新知
矩形是特殊的平行四边形.
有一个角是直角的平行四边形叫做矩形.
矩形的定义:
矩形的探究路径:
师生互动,探究新知
┐
A
B
C
D
有一个角是直角的平行四边形叫做矩形.
对称性:
边:
角:
对角线:
定义
性质
判定
A
B
C
D
┐
A
B
C
D
有一个角是直角
师生互动,探究新知
对称性
边
角
对角线
中心对称图形
轴对称图形
对边平行且相等
对角相等
邻角互补
四个角都是直角
邻边垂直
矩形的性质
平行四边形的
一般性质
对角线互相平分
矩形的特殊性质
O
对角线相等
┐
A
B
C
D
对称性
边
师生互动,探究新知
矩形的四个角都是直角
符号语言:
∵四边形ABCD是矩形,
∴________________________.
猜想:
定理
∠A=∠B=∠C=∠D=90
矩形的特殊性质:
证明
已知:如图,四边形ABCD是矩形,
求证:∠A=∠B=∠C=∠D=90 .
对称性
边
对角线
师生互动,探究新知
矩形的特殊性质:
矩形的对角线相等
符号语言:
∵______________________,
∴________________________.
猜想:
定理
AC=BD
四边形ABCD是矩形
┐
A
B
C
D
O
证明
已知:如图,四边形ABCD是矩形,
求证:AC=BD.
矩形的探究路径:
师生互动,探究新知
有一个角是直角的平行四边形叫做矩形.
对称性:
边:
角:
对角线:
定义
性质
判定
中心对称图形+轴对称图形
对边平行且相等
四个角都是直角
相等且互相平分
┐
A
B
C
D
O
应用知识,解决问题
练习1 如图,在矩形ABCD中对角线AC与BD相交于点O(1)若AB=6,BC=8,则AC=______,OB=_______.
5
10
6
(2)若AB=6,BC=8,求△ BOC与△ AOB的周长之差.
8
解题思路: BC- AB=2
A
B
C
D
边
例1 如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形的周长和是86 cm,矩形的对角线长是13 cm,那么该矩形的周长是多少?
应用知识,解决问题
O
应用知识,解决问题
练习2 如图,在矩形ABCD中对角线AC与BD相交于点O ,∠AOB=60° , AB=4,求对角线的长。
60°
4
解题指南:
当对角线的夹角为60 °或120 °时,利用等边三角形解决问题.
应用知识,解决问题
练习3 如图,矩形纸片ABCD中,AD=4cm,把纸片沿直线AC折叠,点B落在E处,AE交DC于点O,若AO=5cm,则AB的长为( )
A.9cm B.8cm C.7cm D.6cm
B
4cm
5cm
1
2
3
边
课堂小结,交流评价
本节课你有哪些收获?
一个路径:
二个主要思想方法:
三个特殊性质:
“一二三”
1.轴对称图形;
2.四个角都是直角;
3.对角线相等.
定义 性质 判定
类比思想、猜想思想
应用
你的人生是旷野!
课后作业,提升巩固
必做题:教科书第100页,练习2、练习3;
选做题:如图,矩形ABCD沿着直线BD折叠,使点C落在C′处, BC′交AD于点E,已知AD=8,AB=4,求△BED的面积;
实践作业:请用矩形设计一个优美的图案.
课后作业
