19.1.1 矩形的性质 课件(共24张PPT)
文档属性
| 名称 | 19.1.1 矩形的性质 课件(共24张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 399.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 10:01:29 | ||
图片预览








文档简介
遨游数学世界 探究几何奥秘
——我们一起学数学
第19章 矩形、菱形与正方形
1.矩形的性质
19.1 矩形
第19章 矩形、菱形与正方形
华东师范大学出版社
2.通过观察、猜想、验证并证明矩形的性质.
1.借助几何直观,基于一般与特殊的关系理解矩形的概念.
3.会用矩形的定义和性质解决简单问题.
学习目标
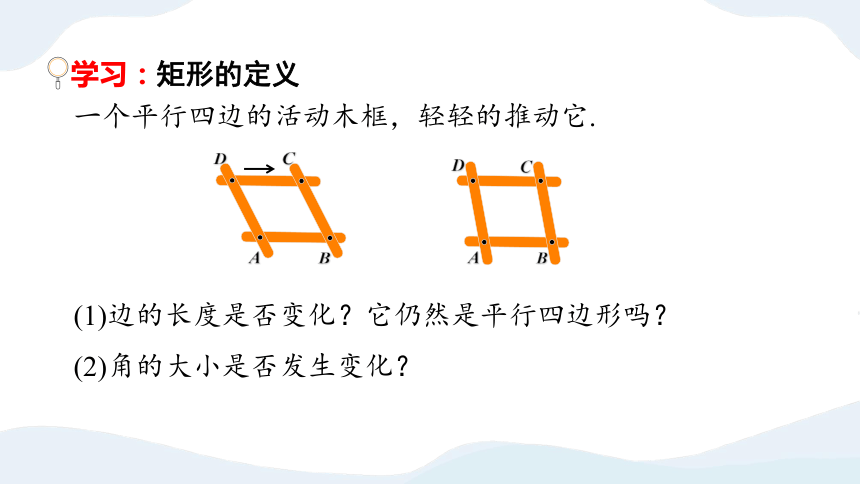
一个平行四边的活动木框,轻轻的推动它.
(1)边的长度是否变化?它仍然是平行四边形吗?
(2)角的大小是否发生变化?
B
C
D
A
B
C
D
A
学习:矩形的定义
定义:有一个角是直角的平行四边形叫做矩形.
直角
平行四边形
∵在□ABCD中∠A=90°,
∴□ABCD是矩形.
∵四边形ABCD是矩形,
∴四边形ABCD是平行四边形,且∠A=90°.
几何语言:
矩形
有一个角是直角
平行四边形
C
A
B
D
C
A
B
D
→矩形ABCD
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的一般性质
知识回顾:平行四边形有哪些性质?
矩形也具有平行四边形的一般性质.
探究:矩形的性质
对边平行且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}矩形的特殊性质
思考 矩形是不是轴对称图形? 如果是,请同学们折一折,看看有几条对称轴?
矩形是轴对称图形,有2条对称轴.
轴对称图形
对称轴为通过对边中点的直线.
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的一般性质
对边平行且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}矩形的特殊性质
准备工作:拿出直尺、量角器、矩形纸片,并连接矩形纸片对角线,标出字母.
A
B
C
D
(1)请从边、角、对角线观察矩形纸片,小组交流讨论,提出矩形特殊性质的猜想?
(2)请用量角器、直尺度量;验证你们的猜想是否正确?
矩形的四个角都是直角.
猜想1
矩形的对角线相等.
猜想2
小组合作:
轴对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的
一般性质
对边平行且相等
对角相等
邻角互补
对角线互相平分
中心对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}矩形的特殊性质
特殊到一般的数学思想
(3)讨论完成以后,确定中心发言人汇报探究成果.
猜想1 矩形的四个角都是直角.
证明:∵四边形ABCD是矩形,
∴AD// BC ,∠A=∠C,∠B=∠D.
∴∠A+∠B=180°.
∵∠A=90°,
∴∠B=180°-∠A=90°.
∴∠A=∠C= ∠B=∠D=90°.
即矩形ABCD的四个角都是直角.
已知:矩形ABCD中,∠A=90°.
求证:∠A=∠B=∠C=∠D=90°.
A
D
C
B
方法小结:利用“对角相等、邻角互补”
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D =90°.
几何语言:
矩形的性质定理1 矩形的四个角都是直角.
已知:矩形ABCD中,∠A=90°.
求证:∠A=∠B=∠C=∠D=90°.
证明:∵四边形ABCD是矩形,
∴AD// BC ,∠A=∠C,∠B=∠D.
∴∠A+∠B=180°.
∵∠A=90°,
∴∠B=180°-∠A=90°.
∴∠A=∠C= ∠B=∠D=90°.
即矩形ABCD的四个角都是直角.
A
D
C
B
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AB=DC,∠BAD=∠ADC=90°.
在△ABD和△DCA中,
∵AB=DC,∠DAB=∠ADC,AD= DA,
∴△ABD≌△DCA.
∴AC=DB.
猜想2 矩形的对角线相等.
已知:矩形ABCD中,对角线AC、BD相交于点O.
求证:AC=BD.
A
B
C
D
O
方法小结:证明不在同一个三角形中的两条线段相等,通常证明它们所在的三角形全等.
△ABC≌△DCB≌△BAD≌△CDA
△AOB≌△DOC,△AOD≌△BOC
矩形的性质定理2 矩形的对角线相等.
已知:矩形ABCD中,对角线AC、BD相交于点O.
求证:AC=BD.
∵AC、BD是矩形ABCD的对角线,
∴AC=BD.
几何语言:
证明:∵四边形ABCD是矩形,
∴AB=DC,∠BAD=∠ADC=90°.
在△ABD和△DCA中,
∵AB=DC,∠DAB=∠ADC,AD= DA,
∴△ABD≌△DCA.
∴AC=DB.
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,试找出图中相等的线段与相等的角.
解:相等的线段:
AB=DC, AD=BC;
AC=BD,OA=OB=OD=OC.
相等的角:
∠BAD=∠ABC=∠BCD=∠ADC=90°;
∠2=∠3=∠6=∠7,∠1=∠8=∠4=∠5;
∠10=∠12,∠9=∠11.
12
9
10
11
8
7
6
5
4
3
2
1
A
B
C
D
O
课堂练习
性质总结:
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的一般性质
矩形的
特殊性质
对边平行且相等
对角相等
邻角互补
对角线互相平分
中心对称图形
轴对称
图形
四个角都是直角
对角线
相等
一般方法:
观察
验证
证明
猜想
例1.如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是86cm,矩形的对角线长是13cm,那么该矩形的周长是多少?
A
B
C
D
O
A
D
O
A
B
O
B
C
O
D
C
O
A
B
C
D
O
分析:
已知:AB+BC+CD+DA+2(OA+OB+OC+OD)=86,
AC=BD=13.
求:AB+BC+CD+DA.
↓
2(AC+BD)
=52
=34 (cm)
2.如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°.
求证:AC=2AB
A
B
C
D
O
证明:∵∠AOD=120°,
∴∠AOB=180°-∠AOD=60°.
∵四边形ABCD是矩形,
∴OB=OA,AC=2OA.
∴△ABO是等边三角形.
∴AC=2OA=2AB.
课堂练习
3.如图,在矩形ABCD中,点E在边CD上.将该矩形沿AE折叠,恰好使点D落在边BC上的点F处,如果∠BAF=60°,则∠DAE= .
A
B
D
C
F
E
课堂练习
15°
矩形的性质
矩形具备平行四边形的一般性质
矩形是轴对称图形
矩形的四个角都是直角
矩形的对角线相等
本节课你收获了哪些知识?
探究几何图形性质的一般方法是什么?
解决问题的过程中,体验到哪些数学思想方法?
矩形
矩形的定义
共 性
数学思想
方法
从特殊到一般
有一个角是直角的平行四边形
观察→猜想→验证→证明
课堂小结
特 性
课后作业
矩形的性质作业设计:
必做题1、2、3
选做题4
会用数学的眼光观察世界,会用数学的思维思考世界,
会用数学的语言表达世界!
课后寄语
——我们一起学数学
第19章 矩形、菱形与正方形
1.矩形的性质
19.1 矩形
第19章 矩形、菱形与正方形
华东师范大学出版社
2.通过观察、猜想、验证并证明矩形的性质.
1.借助几何直观,基于一般与特殊的关系理解矩形的概念.
3.会用矩形的定义和性质解决简单问题.
学习目标
一个平行四边的活动木框,轻轻的推动它.
(1)边的长度是否变化?它仍然是平行四边形吗?
(2)角的大小是否发生变化?
B
C
D
A
B
C
D
A
学习:矩形的定义
定义:有一个角是直角的平行四边形叫做矩形.
直角
平行四边形
∵在□ABCD中∠A=90°,
∴□ABCD是矩形.
∵四边形ABCD是矩形,
∴四边形ABCD是平行四边形,且∠A=90°.
几何语言:
矩形
有一个角是直角
平行四边形
C
A
B
D
C
A
B
D
→矩形ABCD
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的一般性质
知识回顾:平行四边形有哪些性质?
矩形也具有平行四边形的一般性质.
探究:矩形的性质
对边平行且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}矩形的特殊性质
思考 矩形是不是轴对称图形? 如果是,请同学们折一折,看看有几条对称轴?
矩形是轴对称图形,有2条对称轴.
轴对称图形
对称轴为通过对边中点的直线.
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的一般性质
对边平行且相等
对角相等
邻角互补
对角线
互相平分
中心对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}矩形的特殊性质
准备工作:拿出直尺、量角器、矩形纸片,并连接矩形纸片对角线,标出字母.
A
B
C
D
(1)请从边、角、对角线观察矩形纸片,小组交流讨论,提出矩形特殊性质的猜想?
(2)请用量角器、直尺度量;验证你们的猜想是否正确?
矩形的四个角都是直角.
猜想1
矩形的对角线相等.
猜想2
小组合作:
轴对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的
一般性质
对边平行且相等
对角相等
邻角互补
对角线互相平分
中心对称图形
{5940675A-B579-460E-94D1-54222C63F5DA}矩形的特殊性质
特殊到一般的数学思想
(3)讨论完成以后,确定中心发言人汇报探究成果.
猜想1 矩形的四个角都是直角.
证明:∵四边形ABCD是矩形,
∴AD// BC ,∠A=∠C,∠B=∠D.
∴∠A+∠B=180°.
∵∠A=90°,
∴∠B=180°-∠A=90°.
∴∠A=∠C= ∠B=∠D=90°.
即矩形ABCD的四个角都是直角.
已知:矩形ABCD中,∠A=90°.
求证:∠A=∠B=∠C=∠D=90°.
A
D
C
B
方法小结:利用“对角相等、邻角互补”
∵四边形ABCD是矩形,
∴∠A=∠B=∠C=∠D =90°.
几何语言:
矩形的性质定理1 矩形的四个角都是直角.
已知:矩形ABCD中,∠A=90°.
求证:∠A=∠B=∠C=∠D=90°.
证明:∵四边形ABCD是矩形,
∴AD// BC ,∠A=∠C,∠B=∠D.
∴∠A+∠B=180°.
∵∠A=90°,
∴∠B=180°-∠A=90°.
∴∠A=∠C= ∠B=∠D=90°.
即矩形ABCD的四个角都是直角.
A
D
C
B
A
B
C
D
O
证明:∵四边形ABCD是矩形,
∴AB=DC,∠BAD=∠ADC=90°.
在△ABD和△DCA中,
∵AB=DC,∠DAB=∠ADC,AD= DA,
∴△ABD≌△DCA.
∴AC=DB.
猜想2 矩形的对角线相等.
已知:矩形ABCD中,对角线AC、BD相交于点O.
求证:AC=BD.
A
B
C
D
O
方法小结:证明不在同一个三角形中的两条线段相等,通常证明它们所在的三角形全等.
△ABC≌△DCB≌△BAD≌△CDA
△AOB≌△DOC,△AOD≌△BOC
矩形的性质定理2 矩形的对角线相等.
已知:矩形ABCD中,对角线AC、BD相交于点O.
求证:AC=BD.
∵AC、BD是矩形ABCD的对角线,
∴AC=BD.
几何语言:
证明:∵四边形ABCD是矩形,
∴AB=DC,∠BAD=∠ADC=90°.
在△ABD和△DCA中,
∵AB=DC,∠DAB=∠ADC,AD= DA,
∴△ABD≌△DCA.
∴AC=DB.
1.如图,在矩形ABCD中,对角线AC与BD相交于点O,试找出图中相等的线段与相等的角.
解:相等的线段:
AB=DC, AD=BC;
AC=BD,OA=OB=OD=OC.
相等的角:
∠BAD=∠ABC=∠BCD=∠ADC=90°;
∠2=∠3=∠6=∠7,∠1=∠8=∠4=∠5;
∠10=∠12,∠9=∠11.
12
9
10
11
8
7
6
5
4
3
2
1
A
B
C
D
O
课堂练习
性质总结:
{5940675A-B579-460E-94D1-54222C63F5DA}
对称性
边
角
对角线
平行四边形的一般性质
矩形的
特殊性质
对边平行且相等
对角相等
邻角互补
对角线互相平分
中心对称图形
轴对称
图形
四个角都是直角
对角线
相等
一般方法:
观察
验证
证明
猜想
例1.如图,矩形ABCD被两条对角线分成四个小三角形,如果四个小三角形周长的和是86cm,矩形的对角线长是13cm,那么该矩形的周长是多少?
A
B
C
D
O
A
D
O
A
B
O
B
C
O
D
C
O
A
B
C
D
O
分析:
已知:AB+BC+CD+DA+2(OA+OB+OC+OD)=86,
AC=BD=13.
求:AB+BC+CD+DA.
↓
2(AC+BD)
=52
=34 (cm)
2.如图,矩形ABCD的两条对角线相交于点O,∠AOD=120°.
求证:AC=2AB
A
B
C
D
O
证明:∵∠AOD=120°,
∴∠AOB=180°-∠AOD=60°.
∵四边形ABCD是矩形,
∴OB=OA,AC=2OA.
∴△ABO是等边三角形.
∴AC=2OA=2AB.
课堂练习
3.如图,在矩形ABCD中,点E在边CD上.将该矩形沿AE折叠,恰好使点D落在边BC上的点F处,如果∠BAF=60°,则∠DAE= .
A
B
D
C
F
E
课堂练习
15°
矩形的性质
矩形具备平行四边形的一般性质
矩形是轴对称图形
矩形的四个角都是直角
矩形的对角线相等
本节课你收获了哪些知识?
探究几何图形性质的一般方法是什么?
解决问题的过程中,体验到哪些数学思想方法?
矩形
矩形的定义
共 性
数学思想
方法
从特殊到一般
有一个角是直角的平行四边形
观察→猜想→验证→证明
课堂小结
特 性
课后作业
矩形的性质作业设计:
必做题1、2、3
选做题4
会用数学的眼光观察世界,会用数学的思维思考世界,
会用数学的语言表达世界!
课后寄语
