5.1.2+弧度制 课件(共18张PPT)-2023-2024学年高一数学同步精品课件(人教A版2019必修第一册)
文档属性
| 名称 | 5.1.2+弧度制 课件(共18张PPT)-2023-2024学年高一数学同步精品课件(人教A版2019必修第一册) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-07-08 13:37:36 | ||
图片预览




文档简介
5.1.2弧度制
复习导入
复习导入
生活中在度量时,会用到不同的单位制.比如,度量长度可以用米、英尺、码等不同的单位制; 度量质量可以用千克、磅等不同的单位制.
问题:角的度量单位是什么?换算的进制是多少?它是否也能用不同的单位制呢?是否可以用十进制的实数来度量角的大小?
新知探究
活动1:准备一张半圆纸板、一把刻度直尺、若干细线。通过小组合作,试试运用现有的实验用具, 在这张半圆纸上标出 36°的角.
?
先用细线度量半圆弧长, 然后再用刻度尺,将细线分成 5 份, 其中一份弧长所对的角就是 36° 的角.
?
思考:通过弧长,我们可以量出 36°的角,那我们可以直接用弧长来衡量角的大小吗?
?
新知探究
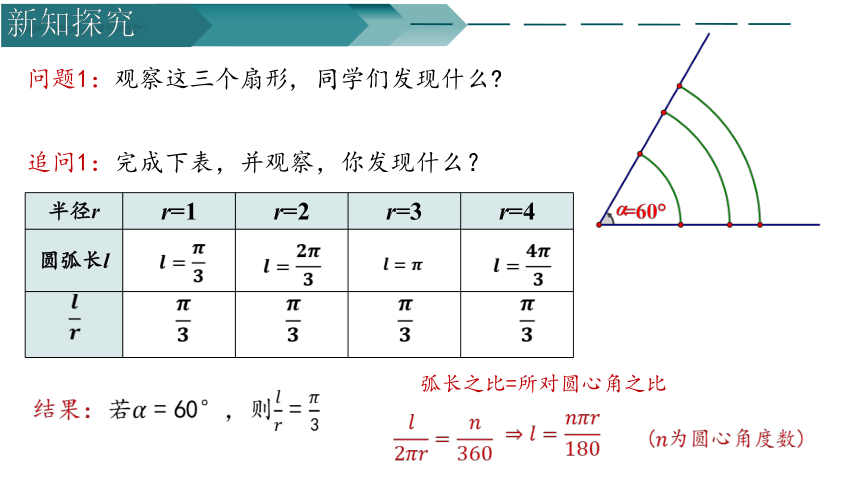
问题1:观察这三个扇形, 同学们发现什么?
追问1:完成下表,并观察,你发现什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}半径r
r=1
r=2
r=3
r=4
圆弧长l
????=????????
?
????=????????????
?
????=????
?
????=????????????
?
????????
?
????????
?
????????
?
????????
?
????????
?
结果:若????=60°,则????????=????3
?
弧长之比=所对圆心角之比
????2????????=????360
?
?????=????????????180
?
(????为圆心角度数)
?
新知探究
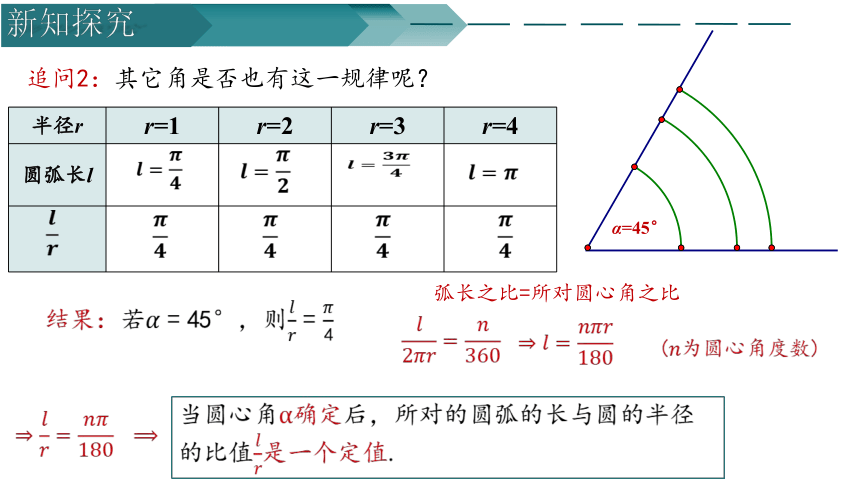
追问2:其它角是否也有这一规律呢?
α=45°
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}半径r
r=1
r=2
r=3
r=4
圆弧长l
????=????????
?
????=????????
?
????=????????????
?
????=????
?
????????
?
????????
?
????????
?
????????
?
????????
?
结果:若????=45°,则????????=????4
?
弧长之比=所对圆心角之比
?????=????????????180
?
(????为圆心角度数)
?
????2????????=????360
?
?????????=????????180 ?
?
当圆心角α确定后,所对的圆弧的长与圆的半径的比值????????是一个定值.
?
新知探究
我们规定:长度等于半径长的圆弧所对的圆心角叫做1弧度的角,弧度单位用符号????????????表示,读作弧度.
在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,则|α|=lr.
?
追问:角度制中,1度角的大小是怎么规定的?
古巴比伦人发现地球公转周期大约为360天
新知探究
活动2:在单位圆中画出下列角度,并换算为弧度制。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}0°
30°
45°
60°
90°
120°
135°
150°
180°
270°
360°
0
?
????6
?
????4
?
????3
?
2????3
?
????2
?
3????4
?
5????6
?
????
?
3????2
?
2????
?
新知探究
????????????°=???? ????????????
?
????°=???????????????? ????????????≈????.????????????????????????????????
?
???? ????????????=(????????????????)°≈????????.????????°
?
练习1:把下列角度化为弧度:
(1)144°; (2)?300°; (3)-210°; (4)22°30’
?
解:(1)144°=144×????180=144????180=4????5. (2)?300°=?300×????180=?5????3.
(3)210°=210×????180=210????180=7????6. (4)22°30’=22.5×????180=45????360=????8.
?
新知探究
变式1-1:把下列弧度化为角度:
(1)π6; (2)?2π3; (3)11π9; (4)4.
?
解:(1)????6=????6×180????°=30°.
(2)?2????3=?2????3×180????°=?120°.
(3)11????9=11????9×180????°=220°.
(4)4=4×(180????)°=(720????)°.
?
练习巩固
变式1-2:把下列角度与弧度进行互化.
(1)120°; (2)-32°; (3)?3????5; (4)????9; (5)112°30’.
?
解:(1)120°=120×????180=2????3.
(2)?32°=?32×????180=?8????45.
(3)?3????5=?3????5×(180????)°=?108°.
(4)????9=????9×(180????)°=1809°≈20°.
(5)112°30’=112.5°=112.5×????180=5????8.
?
练习巩固
变式1-3:把下列各角化成α+2kπ0≤α<2π,k∈Z的形式,并指出它们是哪个象限的角:
(1)23π6; (2)?1680?; (3)?18π7; (4)755?.
?
解:(1)23π6=11π6+2π,是第四象限角;
(2)?1680?=120??5×360?=2π3?10π,是第二象限角;
(3)?18π7=10π7?4π,是第三象限角;
(4)755?=35?+2×360?=7π36+4π,是第一象限角.
?
练习巩固
例6:写利用弧度制证明下列关于扇形的公式:
(1)l=αR; (2)S=12αR2; (3)S=12lR.
其中R是圆的半径,α(0<α<2π)为圆心角,l是扇形的弧长,S是扇形的面积.
?
证明:由公式|????|=????????可得:????=????????.下面证明(2)(3).
半径为????,圆心角为????°的扇形的弧长公式和面积公式分别是:
????=????????????180,????=????????????2360,将????°转换为弧度制,得:????=????????180,于是,????=12????????2.
将????=????????代入上式,即得????=12????????.
显然,弧度制下的弧长公式和扇形面积公式形式简单了.在今后的学习中,我们还将进一步看到弧度制带来的便利.
?
练习巩固
弧长公式:????=????????; 扇形面积公式:????=12????????2=12????????
?
练习2:已知扇形的周长为10cm,面积为4cm2,求扇形圆心角的弧度数.
?
解:设扇形圆心角的弧度数为????(0当????1=1时,???? =8,此时,????=8 ????????????,舍去.
当????2=4时,???? =2,此时,????=12 ????????????.
综上所述,扇形圆心角的弧度数为12 ????????????.
?
练习巩固
变式2-1:已知一扇形的圆心角是150°,半径为12,求扇形的面积.
解:设扇形的弧长为????,
∵圆心角150°=150×????180=5????6 ????????????.
∴扇形弧长???? =|????|?????=5????6×12=10????,
于是,扇形的面积????=12?????????=12×10????×12=60????.
?
练习巩固
变式2-2:扇形圆心角为αα>0,周长为C,面积为S,所在圆半径为r.
(1)若α=90°,r=10cm,求扇形的弧长及该弧所在的弓形的面积
(2)若C=6cm,S=2cm2,求α的值.
?
解:(1)设弧长为l,弓形面积为S1,则α=90°=π2,r=10,l=π2×10=5π????????,
S1=S?S△=12×5π×10?12×10×10 =25π?50????????2;
(2)由已知得2r+l=612lr=2,解得r=1l=4或r=2l=2,
∴α=4或α=1
?
练习巩固
练习3:已知一扇形的圆心角为α,半径为R,弧长为l.
(1)若α=60°,R=6,求扇形的弧长l;
(2)若扇形面积为16,求扇形周长的最小值,及此时扇形的圆心角α.
?
解:(1)因为α=60°=π3,R=6,所以扇形的弧长l=αR=2π;
(2)由扇形面积S=12αR2=12lR=16,得l=32R,则
扇形周长为l+2R=32R+2R≥232R×2R=16,当且仅当32R=2R,即R=4时,取等号,
此时,12α×42=16,所以α=2,
所以扇形周长的最小值为16,此时α=2.
?
小结
复习导入
复习导入
生活中在度量时,会用到不同的单位制.比如,度量长度可以用米、英尺、码等不同的单位制; 度量质量可以用千克、磅等不同的单位制.
问题:角的度量单位是什么?换算的进制是多少?它是否也能用不同的单位制呢?是否可以用十进制的实数来度量角的大小?
新知探究
活动1:准备一张半圆纸板、一把刻度直尺、若干细线。通过小组合作,试试运用现有的实验用具, 在这张半圆纸上标出 36°的角.
?
先用细线度量半圆弧长, 然后再用刻度尺,将细线分成 5 份, 其中一份弧长所对的角就是 36° 的角.
?
思考:通过弧长,我们可以量出 36°的角,那我们可以直接用弧长来衡量角的大小吗?
?
新知探究
问题1:观察这三个扇形, 同学们发现什么?
追问1:完成下表,并观察,你发现什么?
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}半径r
r=1
r=2
r=3
r=4
圆弧长l
????=????????
?
????=????????????
?
????=????
?
????=????????????
?
????????
?
????????
?
????????
?
????????
?
????????
?
结果:若????=60°,则????????=????3
?
弧长之比=所对圆心角之比
????2????????=????360
?
?????=????????????180
?
(????为圆心角度数)
?
新知探究
追问2:其它角是否也有这一规律呢?
α=45°
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}半径r
r=1
r=2
r=3
r=4
圆弧长l
????=????????
?
????=????????
?
????=????????????
?
????=????
?
????????
?
????????
?
????????
?
????????
?
????????
?
结果:若????=45°,则????????=????4
?
弧长之比=所对圆心角之比
?????=????????????180
?
(????为圆心角度数)
?
????2????????=????360
?
?????????=????????180 ?
?
当圆心角α确定后,所对的圆弧的长与圆的半径的比值????????是一个定值.
?
新知探究
我们规定:长度等于半径长的圆弧所对的圆心角叫做1弧度的角,弧度单位用符号????????????表示,读作弧度.
在半径为r的圆中,弧长为l的弧所对的圆心角为α rad,则|α|=lr.
?
追问:角度制中,1度角的大小是怎么规定的?
古巴比伦人发现地球公转周期大约为360天
新知探究
活动2:在单位圆中画出下列角度,并换算为弧度制。
{5C22544A-7EE6-4342-B048-85BDC9FD1C3A}0°
30°
45°
60°
90°
120°
135°
150°
180°
270°
360°
0
?
????6
?
????4
?
????3
?
2????3
?
????2
?
3????4
?
5????6
?
????
?
3????2
?
2????
?
新知探究
????????????°=???? ????????????
?
????°=???????????????? ????????????≈????.????????????????????????????????
?
???? ????????????=(????????????????)°≈????????.????????°
?
练习1:把下列角度化为弧度:
(1)144°; (2)?300°; (3)-210°; (4)22°30’
?
解:(1)144°=144×????180=144????180=4????5. (2)?300°=?300×????180=?5????3.
(3)210°=210×????180=210????180=7????6. (4)22°30’=22.5×????180=45????360=????8.
?
新知探究
变式1-1:把下列弧度化为角度:
(1)π6; (2)?2π3; (3)11π9; (4)4.
?
解:(1)????6=????6×180????°=30°.
(2)?2????3=?2????3×180????°=?120°.
(3)11????9=11????9×180????°=220°.
(4)4=4×(180????)°=(720????)°.
?
练习巩固
变式1-2:把下列角度与弧度进行互化.
(1)120°; (2)-32°; (3)?3????5; (4)????9; (5)112°30’.
?
解:(1)120°=120×????180=2????3.
(2)?32°=?32×????180=?8????45.
(3)?3????5=?3????5×(180????)°=?108°.
(4)????9=????9×(180????)°=1809°≈20°.
(5)112°30’=112.5°=112.5×????180=5????8.
?
练习巩固
变式1-3:把下列各角化成α+2kπ0≤α<2π,k∈Z的形式,并指出它们是哪个象限的角:
(1)23π6; (2)?1680?; (3)?18π7; (4)755?.
?
解:(1)23π6=11π6+2π,是第四象限角;
(2)?1680?=120??5×360?=2π3?10π,是第二象限角;
(3)?18π7=10π7?4π,是第三象限角;
(4)755?=35?+2×360?=7π36+4π,是第一象限角.
?
练习巩固
例6:写利用弧度制证明下列关于扇形的公式:
(1)l=αR; (2)S=12αR2; (3)S=12lR.
其中R是圆的半径,α(0<α<2π)为圆心角,l是扇形的弧长,S是扇形的面积.
?
证明:由公式|????|=????????可得:????=????????.下面证明(2)(3).
半径为????,圆心角为????°的扇形的弧长公式和面积公式分别是:
????=????????????180,????=????????????2360,将????°转换为弧度制,得:????=????????180,于是,????=12????????2.
将????=????????代入上式,即得????=12????????.
显然,弧度制下的弧长公式和扇形面积公式形式简单了.在今后的学习中,我们还将进一步看到弧度制带来的便利.
?
练习巩固
弧长公式:????=????????; 扇形面积公式:????=12????????2=12????????
?
练习2:已知扇形的周长为10cm,面积为4cm2,求扇形圆心角的弧度数.
?
解:设扇形圆心角的弧度数为????(0当????1=1时,???? =8,此时,????=8 ????????????,舍去.
当????2=4时,???? =2,此时,????=12 ????????????.
综上所述,扇形圆心角的弧度数为12 ????????????.
?
练习巩固
变式2-1:已知一扇形的圆心角是150°,半径为12,求扇形的面积.
解:设扇形的弧长为????,
∵圆心角150°=150×????180=5????6 ????????????.
∴扇形弧长???? =|????|?????=5????6×12=10????,
于是,扇形的面积????=12?????????=12×10????×12=60????.
?
练习巩固
变式2-2:扇形圆心角为αα>0,周长为C,面积为S,所在圆半径为r.
(1)若α=90°,r=10cm,求扇形的弧长及该弧所在的弓形的面积
(2)若C=6cm,S=2cm2,求α的值.
?
解:(1)设弧长为l,弓形面积为S1,则α=90°=π2,r=10,l=π2×10=5π????????,
S1=S?S△=12×5π×10?12×10×10 =25π?50????????2;
(2)由已知得2r+l=612lr=2,解得r=1l=4或r=2l=2,
∴α=4或α=1
?
练习巩固
练习3:已知一扇形的圆心角为α,半径为R,弧长为l.
(1)若α=60°,R=6,求扇形的弧长l;
(2)若扇形面积为16,求扇形周长的最小值,及此时扇形的圆心角α.
?
解:(1)因为α=60°=π3,R=6,所以扇形的弧长l=αR=2π;
(2)由扇形面积S=12αR2=12lR=16,得l=32R,则
扇形周长为l+2R=32R+2R≥232R×2R=16,当且仅当32R=2R,即R=4时,取等号,
此时,12α×42=16,所以α=2,
所以扇形周长的最小值为16,此时α=2.
?
小结
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
