五年级下册数学人教版《总复习——因数与倍数》课件(共21张PPT)
文档属性
| 名称 | 五年级下册数学人教版《总复习——因数与倍数》课件(共21张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 06:48:14 | ||
图片预览








文档简介
(共21张PPT)
总复习——数与代数(1)
因数与倍数
在整数除法中,如果商是整数且没有余数(或者说余数为0),
我们就说除数是被除数的因数(也称约数),
被除数是除数的倍数。
复习因数与倍数的意义
例如,
12÷2=6,
说2是12的因数,12是2的倍数。
12÷6=2,
说6是12的因数,12是6的倍数。
2×6=12,
说2和6是12的因数,12是2和6的倍数。
可写成
可写成
注意:倍数和因数是相互依存的。没有倍数就不存在因数,没有因数就不存在倍数,不能单独说一个数是倍数或因数。
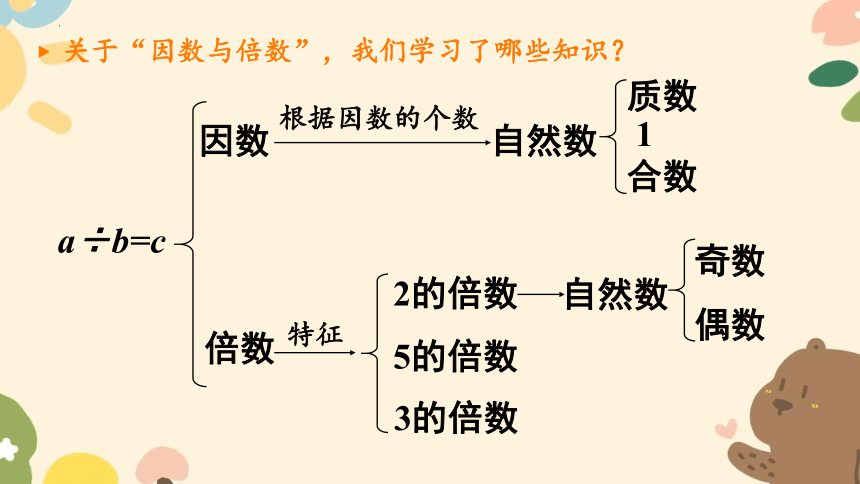
关于“因数与倍数”,我们学习了哪些知识?
a÷b=c
因数
根据因数的个数
自然数
质数
偶数
倍数
特征
2的倍数
5的倍数
3的倍数
自然数
奇数
合数
1
知识拓展
在第四单元《分数的意义和性质》中,我们还学习了哪些与“因数与倍数”有关的知识?
公因数:
最大公因数:
公倍数:
最小公倍数:
两个自然数公有的因数叫公因数,最小的公因数是1。
最大的公因数叫最大公因数。
两个自然数的公有的倍数叫公倍数。
公倍数中最小的一个(0除外)叫最小公倍数,没有最大的公倍数。
下面哪些数是2的倍数?哪些是3的倍数?
哪些是5的倍数?哪些是质数?哪些是合数?
哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56 79 87 195 204 630 22 31 57 65 78 83
根据2、3、5的倍数的特征,质数和合数的特征,奇数和偶数的特征判断。
练习巩固(书118页第1题)
回顾旧知
2的倍数特征:
3的倍数特征:
5的倍数特征:
个位上是0、2、4、6、8的数都是2的倍数。
各位上的数的和是3的倍数的数
都是3的倍数。
个位上是0或5的数都是5的倍数。
下面哪些数是2的倍数?哪些是3的倍数?
哪些是5的倍数?哪些是质数?哪些是合数?
哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56 79 87 195 204 630 22 31 57 65 78 83
2的倍数:56、204、630、22、78;
3的倍数:87、195、204、630、57、78;
5的倍数:195、630、65;
练习巩固(书118页第1题)
回顾旧知
质数:
合数:
20以内的质数:
只有1和它本身两个因数的数叫做质数(素数)。
除了1和它本身还有其他因数的数叫做合数。最小的合数是4。
2、3、5、7、11、13、17、19
按照因数的个数分类,自然数可以分为质数、合数和1。(1既不是质数也不是合数。)
下面哪些数是2的倍数?哪些是3的倍数?
哪些是5的倍数?哪些是质数?哪些是合数?
哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56 79 87 195 204 630 22 31 57 65 78 83
质数:79、31、83;
合数:56、87、195、204、630、22、57、65、78;
练习巩固(书118页第1题)
回顾旧知
奇数:
偶数:
整数中,是2的倍数的数叫做偶数(0也是偶数)。
不是2的倍数的数叫做奇数。
按照是不是2的倍数分类,自然数可以分为奇数和偶数。
练习巩固(书118页第1题)
下面哪些数是2的倍数?哪些是3的倍数?
哪些是5的倍数?哪些是质数?哪些是合数?
哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56 79 87 195 204 630 22 31 57 65 78 83
奇数:79、87、195、31、57、65、83;
偶数:56、204、630、22、78。
练习巩固(书118页第2题)
(1)两个合数相乘,积还是合数。
(2)两个不同质数的公因数只有1。
(3)一个数的因数一定比它的倍数小。
(4)两个数的最小公倍数是这两个数最大公因数的倍数。
(5)最小的质数是1。
判断下面的说法是否正确,并说一说你的理由。
√
√
×
√
×
一个数的最大因数是它本身,一个数的最小倍数是它本身。
因此一个数的因数有可能与它的倍数相等。
1既不是质数也不是合数。
练习巩固(书118页第3题)
3. 找出下面每组数的最大公因数和最小公倍数,以其中一组为例,说一说你是怎样找到的。
4 和 5
6 和 16
15 和 20
10 和 8
3 和 9
列举法
筛选法
分解质因数法
短除法
求两个数的最大公因数的方法有:
较小的数
任何数
回顾旧知
列举法
求两个数的最小公倍数的方法有:
较小的数
任何数
筛选法
分解质因数法
短除法
回顾旧知
练习巩固(书118页第3题)
3. 找出下面每组数的最大公因数和最小公倍数,以其中一组为例,说一说你是怎样找到的。
4 和 5
6 和 16
15 和 20
10 和 8
3 和 9
4和5最大公因数是1,最小公倍数是20。
6和16最大公因数是2,最小公倍数是48。
15和20最大公因数是5,最小公倍数是60。
10和8最大公因数是2,最小公倍数是40。
3和9最大公因数是3,最小公倍数是9。
4. 食品店有70多个松花蛋。如果把它们装进4个一排的蛋托中,正好装完;如果把它们装进6个一排的蛋托中,也正好装完。一共有多少个松花蛋?
练习巩固(书118页第4题)
松花蛋的个数是4的倍数。
松花蛋的个数是6的倍数。
松花蛋的个数是4和6的公倍数。
6和4的公倍数中比70多一点的是72,
所以一共有72个松花蛋。
拓展练习
1.填一填。
(1)一个三位数23□,如果这个数是2的倍数, □可以填( );如果这个数是5的倍数, □可以填( );如果这个数是3的倍数,□可以填( )。
0,2,4,6,8
0,5
1,4,7
拓展练习
(2)一个三位数38 □ ,当它是偶数时,最小填( ):当它是3的倍数时,最大填( );当它既是奇数,又是3的倍数时,填( )。
0
7
1,7
拓展练习
2. 小明爸爸的电话号码是个八位数:
86 ABCDEF。
这个电话号码满足下面的条件:
A是10以内2的最大倍数;B是最小的合数;C是最小的质数;D加上1就是最小的合数;E是任何自然数的因数;F既不是质数,也不是合数。这个电话号码是( )
86842311
拓展练习
3. 找与众不同的数。
7 4 13 2 5 1 9 19
(答案不唯一)
如:1既不是质数也不是合数;2是最小的质数,而且是唯一一个既是偶数又是质数的数……
总复习——数与代数(1)
因数与倍数
在整数除法中,如果商是整数且没有余数(或者说余数为0),
我们就说除数是被除数的因数(也称约数),
被除数是除数的倍数。
复习因数与倍数的意义
例如,
12÷2=6,
说2是12的因数,12是2的倍数。
12÷6=2,
说6是12的因数,12是6的倍数。
2×6=12,
说2和6是12的因数,12是2和6的倍数。
可写成
可写成
注意:倍数和因数是相互依存的。没有倍数就不存在因数,没有因数就不存在倍数,不能单独说一个数是倍数或因数。
关于“因数与倍数”,我们学习了哪些知识?
a÷b=c
因数
根据因数的个数
自然数
质数
偶数
倍数
特征
2的倍数
5的倍数
3的倍数
自然数
奇数
合数
1
知识拓展
在第四单元《分数的意义和性质》中,我们还学习了哪些与“因数与倍数”有关的知识?
公因数:
最大公因数:
公倍数:
最小公倍数:
两个自然数公有的因数叫公因数,最小的公因数是1。
最大的公因数叫最大公因数。
两个自然数的公有的倍数叫公倍数。
公倍数中最小的一个(0除外)叫最小公倍数,没有最大的公倍数。
下面哪些数是2的倍数?哪些是3的倍数?
哪些是5的倍数?哪些是质数?哪些是合数?
哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56 79 87 195 204 630 22 31 57 65 78 83
根据2、3、5的倍数的特征,质数和合数的特征,奇数和偶数的特征判断。
练习巩固(书118页第1题)
回顾旧知
2的倍数特征:
3的倍数特征:
5的倍数特征:
个位上是0、2、4、6、8的数都是2的倍数。
各位上的数的和是3的倍数的数
都是3的倍数。
个位上是0或5的数都是5的倍数。
下面哪些数是2的倍数?哪些是3的倍数?
哪些是5的倍数?哪些是质数?哪些是合数?
哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56 79 87 195 204 630 22 31 57 65 78 83
2的倍数:56、204、630、22、78;
3的倍数:87、195、204、630、57、78;
5的倍数:195、630、65;
练习巩固(书118页第1题)
回顾旧知
质数:
合数:
20以内的质数:
只有1和它本身两个因数的数叫做质数(素数)。
除了1和它本身还有其他因数的数叫做合数。最小的合数是4。
2、3、5、7、11、13、17、19
按照因数的个数分类,自然数可以分为质数、合数和1。(1既不是质数也不是合数。)
下面哪些数是2的倍数?哪些是3的倍数?
哪些是5的倍数?哪些是质数?哪些是合数?
哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56 79 87 195 204 630 22 31 57 65 78 83
质数:79、31、83;
合数:56、87、195、204、630、22、57、65、78;
练习巩固(书118页第1题)
回顾旧知
奇数:
偶数:
整数中,是2的倍数的数叫做偶数(0也是偶数)。
不是2的倍数的数叫做奇数。
按照是不是2的倍数分类,自然数可以分为奇数和偶数。
练习巩固(书118页第1题)
下面哪些数是2的倍数?哪些是3的倍数?
哪些是5的倍数?哪些是质数?哪些是合数?
哪些是奇数?哪些是偶数?说一说你是怎样判断的。
56 79 87 195 204 630 22 31 57 65 78 83
奇数:79、87、195、31、57、65、83;
偶数:56、204、630、22、78。
练习巩固(书118页第2题)
(1)两个合数相乘,积还是合数。
(2)两个不同质数的公因数只有1。
(3)一个数的因数一定比它的倍数小。
(4)两个数的最小公倍数是这两个数最大公因数的倍数。
(5)最小的质数是1。
判断下面的说法是否正确,并说一说你的理由。
√
√
×
√
×
一个数的最大因数是它本身,一个数的最小倍数是它本身。
因此一个数的因数有可能与它的倍数相等。
1既不是质数也不是合数。
练习巩固(书118页第3题)
3. 找出下面每组数的最大公因数和最小公倍数,以其中一组为例,说一说你是怎样找到的。
4 和 5
6 和 16
15 和 20
10 和 8
3 和 9
列举法
筛选法
分解质因数法
短除法
求两个数的最大公因数的方法有:
较小的数
任何数
回顾旧知
列举法
求两个数的最小公倍数的方法有:
较小的数
任何数
筛选法
分解质因数法
短除法
回顾旧知
练习巩固(书118页第3题)
3. 找出下面每组数的最大公因数和最小公倍数,以其中一组为例,说一说你是怎样找到的。
4 和 5
6 和 16
15 和 20
10 和 8
3 和 9
4和5最大公因数是1,最小公倍数是20。
6和16最大公因数是2,最小公倍数是48。
15和20最大公因数是5,最小公倍数是60。
10和8最大公因数是2,最小公倍数是40。
3和9最大公因数是3,最小公倍数是9。
4. 食品店有70多个松花蛋。如果把它们装进4个一排的蛋托中,正好装完;如果把它们装进6个一排的蛋托中,也正好装完。一共有多少个松花蛋?
练习巩固(书118页第4题)
松花蛋的个数是4的倍数。
松花蛋的个数是6的倍数。
松花蛋的个数是4和6的公倍数。
6和4的公倍数中比70多一点的是72,
所以一共有72个松花蛋。
拓展练习
1.填一填。
(1)一个三位数23□,如果这个数是2的倍数, □可以填( );如果这个数是5的倍数, □可以填( );如果这个数是3的倍数,□可以填( )。
0,2,4,6,8
0,5
1,4,7
拓展练习
(2)一个三位数38 □ ,当它是偶数时,最小填( ):当它是3的倍数时,最大填( );当它既是奇数,又是3的倍数时,填( )。
0
7
1,7
拓展练习
2. 小明爸爸的电话号码是个八位数:
86 ABCDEF。
这个电话号码满足下面的条件:
A是10以内2的最大倍数;B是最小的合数;C是最小的质数;D加上1就是最小的合数;E是任何自然数的因数;F既不是质数,也不是合数。这个电话号码是( )
86842311
拓展练习
3. 找与众不同的数。
7 4 13 2 5 1 9 19
(答案不唯一)
如:1既不是质数也不是合数;2是最小的质数,而且是唯一一个既是偶数又是质数的数……
