第19章《 一次函数 》单元同步检测试题(含答案)
文档属性
| 名称 | 第19章《 一次函数 》单元同步检测试题(含答案) | 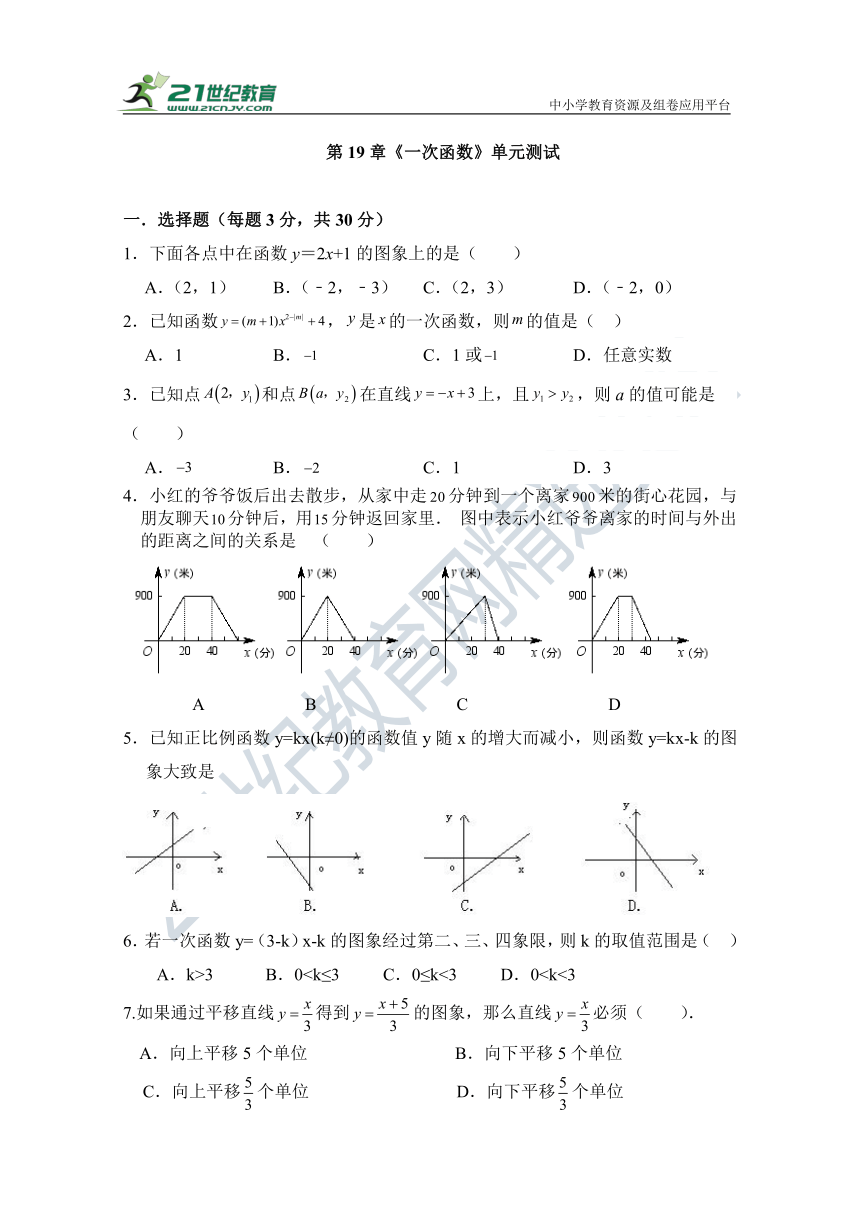 | |
| 格式 | doc | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 15:14:55 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.下面各点中在函数y=2x+1的图象上的是( )
A.(2,1) B.(﹣2,﹣3) C.(2,3) D.(﹣2,0)
2.已知函数,是的一次函数,则的值是( )
A.1 B. C.1或 D.任意实数
3.已知点和点在直线上,且,则a的值可能是( )
A. B. C.1 D.3
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则函数y=kx-k的图象大致是
6.若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )
A.k>3 B.07.如果通过平移直线得到的图象,那么直线必须( ).
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
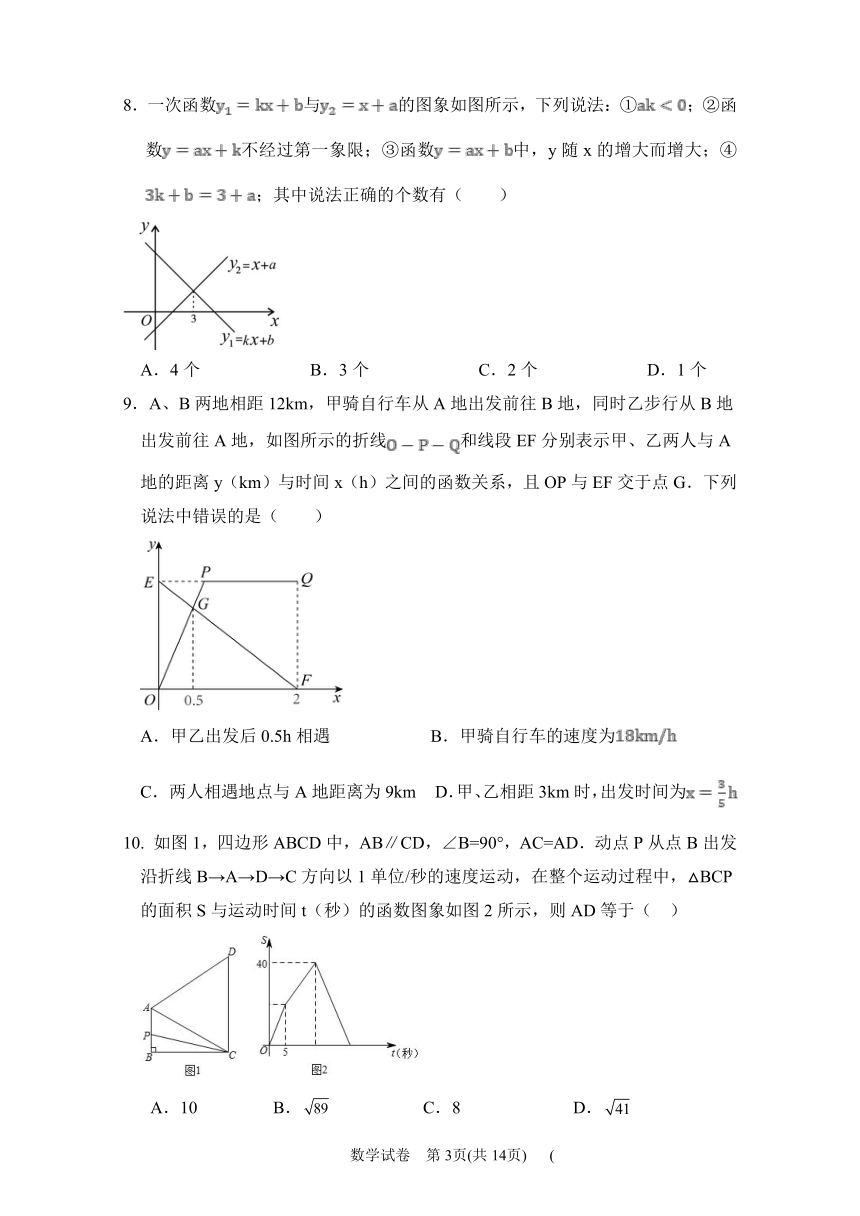
8.一次函数与的图象如图所示,下列说法:①;②函数不经过第一象限;③函数中,y随x的增大而增大;④;其中说法正确的个数有( )
A.4个 B.3个 C.2个 D.1个
9.A、B两地相距12km,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图所示的折线和线段EF分别表示甲、乙两人与A地的距离y(km)与时间x(h)之间的函数关系,且OP与EF交于点G.下列说法中错误的是( )
A.甲乙出发后0.5h相遇 B.甲骑自行车的速度为
C.两人相遇地点与A地距离为9km D.甲、乙相距3km时,出发时间为
10. 如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B→A→D→C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )
A.10 B. C.8 D.
二、填空题(每题3分,共30分)
11.已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1),则此函数的解析式为_________.
12.A(3,y1),B(1,y2)是直线y=kx+3(k>0)上的两点,则y1 y2(填“>”或“<).
13.直角三角形两直角边的长分别为x,y,它的面积为3,则y与x之间的函数关系式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转 而得,则所在直线的解析式是__________.
17.如图所示,已知一次函数的图象与轴的交点坐标为,则不等式的解集为______.
18.如图,在平面直角坐标系中,点在直线上,过点作轴的平行线交直线于点,点均在第一象限,以为边向右作正方形,若,则点的坐标为_____.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知,如图,一次函数的图象经过点P(4,2)和B(0,﹣2),与x轴交于点A.
(1)求一次函数的解析式;
(2)在x轴上存在一点Q,且△ABQ的面积为6,求点Q的坐标.
20.父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了表格.
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答:
(1)如果用h表示距离地面的高度,用t表示温度,写出t与h的关系式;
(2)你能计算出距离地面8千米的高空温度是多少吗?
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.某商场准备购进甲、乙两种服装进行销售,甲种服装每件进价160元,售价220元;乙种服装每件进价120元,售价160元.现计划购进两种服装共100件,其中甲种服装不少于60件.设购进甲种服装x件,两种服装全部售完,商场获利y元.
(1)求y与x之间的函数关系式.
(2)若购进100件服装的总费用不超过15000元,则最大利润为多少元?
24.如图,在平面直角坐标系中,过点B(6,0)的直线AB与y轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线O QUOTE → QUOTE A QUOTE → QUOTE C运动.
(1)求直线BC的解析式.
(2)求 QUOTE ΔOAC QUOTE 的面积.
(3)当 QUOTE ΔOPC QUOTE 的面积是 QUOTE ΔOAC QUOTE 的面积的 QUOTE 14 QUOTE 时,求出这时点P的坐标.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D D D A C B C A
二、填空题(每题3分,共24分)
11. y=2x+1
12. >
13. y=.
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.(1)y=x﹣2;(2)Q点的坐标为(﹣4,0)或(8,0).
20.(1);(2).
21.①5元;②0.5元;③45千克
22.①当03时,y=t-0.6.
②2.4元;6.4元
23.(1)
(2)当时,y最大,最大值为5500元
24.(1)解:设直线BC的解析式是 QUOTE y=kx+b QUOTE ,根据题意得: QUOTE 6=b0=6k+b QUOTE
解得 QUOTE k=-1b=6 QUOTE
则直线的解析式是: QUOTE y=-x+6 QUOTE ;
(2)解:在 QUOTE y=-x+6 QUOTE 中,令 QUOTE y=2 QUOTE ,解得: QUOTE x=4 QUOTE
则 QUOTE SOAC=12×6×4=12 QUOTE ;
(3)解:设 QUOTE OA QUOTE 的解析式是 QUOTE y=ax QUOTE ,则 QUOTE 4a=2 QUOTE ,
解得: QUOTE a=12 QUOTE ,
则直线的解析式是: QUOTE y=12x QUOTE ,
∵当 QUOTE △OPC QUOTE 的面积是 QUOTE △OAC QUOTE 的面积的 QUOTE 14 QUOTE 时,∴P的横坐标是 QUOTE 14×4=1 QUOTE ,
在 QUOTE y=12x QUOTE 中,当 QUOTE x=1 QUOTE 时, QUOTE y=12 QUOTE ,则P的坐标是 QUOTE (1 12) QUOTE ;
在 QUOTE y=-x+6 QUOTE 中, QUOTE x=1 QUOTE 则 QUOTE y=5 QUOTE ,则P的坐标是 QUOTE (1 5) QUOTE
∴ QUOTE P QUOTE 的坐标是: QUOTE P1(1 12) P2(1 5) QUOTE .
数学试卷 第3页(共16页) ( 数学试卷 第4页(共16页)
第19章《一次函数》单元测试
一.选择题(每题3分,共30分)
1.下面各点中在函数y=2x+1的图象上的是( )
A.(2,1) B.(﹣2,﹣3) C.(2,3) D.(﹣2,0)
2.已知函数,是的一次函数,则的值是( )
A.1 B. C.1或 D.任意实数
3.已知点和点在直线上,且,则a的值可能是( )
A. B. C.1 D.3
4.小红的爷爷饭后出去散步,从家中走分钟到一个离家米的街心花园,与朋友聊天分钟后,用分钟返回家里. 图中表示小红爷爷离家的时间与外出的距离之间的关系是 ( )
A B C D
5.已知正比例函数y=kx(k≠0)的函数值y随x的增大而减小,则函数y=kx-k的图象大致是
6.若一次函数y=(3-k)x-k的图象经过第二、三、四象限,则k的取值范围是( )
A.k>3 B.0
A.向上平移5个单位 B.向下平移5个单位
C.向上平移个单位 D.向下平移个单位
8.一次函数与的图象如图所示,下列说法:①;②函数不经过第一象限;③函数中,y随x的增大而增大;④;其中说法正确的个数有( )
A.4个 B.3个 C.2个 D.1个
9.A、B两地相距12km,甲骑自行车从A地出发前往B地,同时乙步行从B地出发前往A地,如图所示的折线和线段EF分别表示甲、乙两人与A地的距离y(km)与时间x(h)之间的函数关系,且OP与EF交于点G.下列说法中错误的是( )
A.甲乙出发后0.5h相遇 B.甲骑自行车的速度为
C.两人相遇地点与A地距离为9km D.甲、乙相距3km时,出发时间为
10. 如图1,四边形ABCD中,AB∥CD,∠B=90°,AC=AD.动点P从点B出发沿折线B→A→D→C方向以1单位/秒的速度运动,在整个运动过程中,△BCP的面积S与运动时间t(秒)的函数图象如图2所示,则AD等于( )
A.10 B. C.8 D.
二、填空题(每题3分,共30分)
11.已知一次函数y=kx+b的图象经过点A(1,3)和B(-1,-1),则此函数的解析式为_________.
12.A(3,y1),B(1,y2)是直线y=kx+3(k>0)上的两点,则y1 y2(填“>”或“<).
13.直角三角形两直角边的长分别为x,y,它的面积为3,则y与x之间的函数关系式为 .
14.一次函数y=(m+2)x+1若y随x的增大而增大,则m的取值范围是___________.
15.如图,一次函数的图象经过A、B两点,则关于x的
不等式的解集是 .
16.如图,在平面直角坐标系中,,由绕点顺时针旋转 而得,则所在直线的解析式是__________.
17.如图所示,已知一次函数的图象与轴的交点坐标为,则不等式的解集为______.
18.如图,在平面直角坐标系中,点在直线上,过点作轴的平行线交直线于点,点均在第一象限,以为边向右作正方形,若,则点的坐标为_____.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.已知,如图,一次函数的图象经过点P(4,2)和B(0,﹣2),与x轴交于点A.
(1)求一次函数的解析式;
(2)在x轴上存在一点Q,且△ABQ的面积为6,求点Q的坐标.
20.父亲告诉小明:“距离地面越高,温度越低,”并给小明出示了表格.
距离地面高度(千米) 0 1 2 3 4 5
温度(℃) 20 14 8 2
根据上表,父亲还给小明出了下面几个问题,你和小明一起回答:
(1)如果用h表示距离地面的高度,用t表示温度,写出t与h的关系式;
(2)你能计算出距离地面8千米的高空温度是多少吗?
21.一农民带了若干千克自产的土豆进城出售,为了方便,他带了一些零钱备用,按市场价售出一些后,又降价出售.售出土豆千克数与他手中持有的钱数(含备用零钱)的关系如图所示,结合图象回答下列问题:
(1)农民自带的零钱是多少?
(2)降价前他每千克土豆出售的价格是多少?
(3)降价后他按每千克0.4元将剩余土豆售完,这时他手中的钱(含备用零钱)是26元,问他一共带了多少千克土豆?
22.如图所示的折线ABC表示从甲地向乙地打长途电话所需的电话费y(元)与通话时间t(分钟)之间的函数关系的图象.(1)写出y与t之间的函数关系式.(2)通话2分钟应付通话费多少元?通话7分钟呢?
23.某商场准备购进甲、乙两种服装进行销售,甲种服装每件进价160元,售价220元;乙种服装每件进价120元,售价160元.现计划购进两种服装共100件,其中甲种服装不少于60件.设购进甲种服装x件,两种服装全部售完,商场获利y元.
(1)求y与x之间的函数关系式.
(2)若购进100件服装的总费用不超过15000元,则最大利润为多少元?
24.如图,在平面直角坐标系中,过点B(6,0)的直线AB与y轴相交于点C(0,6),与直线OA相交于点A且点A纵坐标为2,动点P沿路线O QUOTE → QUOTE A QUOTE → QUOTE C运动.
(1)求直线BC的解析式.
(2)求 QUOTE ΔOAC QUOTE 的面积.
(3)当 QUOTE ΔOPC QUOTE 的面积是 QUOTE ΔOAC QUOTE 的面积的 QUOTE 14 QUOTE 时,求出这时点P的坐标.
答案:
一、选择题(每题3分,共30分)
题号 1 2 3 4 5 6 7 8 9 10
答案 B A D D D A C B C A
二、填空题(每题3分,共24分)
11. y=2x+1
12. >
13. y=.
14.y=x+.
15. X<2
16.
17.y=-x+10.
18. 3820元.
三、解答题(满分46分,19题6分,20、21、22、23、24题每题8分)
19.(1)y=x﹣2;(2)Q点的坐标为(﹣4,0)或(8,0).
20.(1);(2).
21.①5元;②0.5元;③45千克
22.①当0
②2.4元;6.4元
23.(1)
(2)当时,y最大,最大值为5500元
24.(1)解:设直线BC的解析式是 QUOTE y=kx+b QUOTE ,根据题意得: QUOTE 6=b0=6k+b QUOTE
解得 QUOTE k=-1b=6 QUOTE
则直线的解析式是: QUOTE y=-x+6 QUOTE ;
(2)解:在 QUOTE y=-x+6 QUOTE 中,令 QUOTE y=2 QUOTE ,解得: QUOTE x=4 QUOTE
则 QUOTE SOAC=12×6×4=12 QUOTE ;
(3)解:设 QUOTE OA QUOTE 的解析式是 QUOTE y=ax QUOTE ,则 QUOTE 4a=2 QUOTE ,
解得: QUOTE a=12 QUOTE ,
则直线的解析式是: QUOTE y=12x QUOTE ,
∵当 QUOTE △OPC QUOTE 的面积是 QUOTE △OAC QUOTE 的面积的 QUOTE 14 QUOTE 时,∴P的横坐标是 QUOTE 14×4=1 QUOTE ,
在 QUOTE y=12x QUOTE 中,当 QUOTE x=1 QUOTE 时, QUOTE y=12 QUOTE ,则P的坐标是 QUOTE (1 12) QUOTE ;
在 QUOTE y=-x+6 QUOTE 中, QUOTE x=1 QUOTE 则 QUOTE y=5 QUOTE ,则P的坐标是 QUOTE (1 5) QUOTE
∴ QUOTE P QUOTE 的坐标是: QUOTE P1(1 12) P2(1 5) QUOTE .
数学试卷 第3页(共16页) ( 数学试卷 第4页(共16页)
