第八章 二元一次方程组单元同步检测试题(含答案)
文档属性
| 名称 | 第八章 二元一次方程组单元同步检测试题(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 314.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 15:15:50 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
第八章《二元一次方程组》单元检测题
一、选择题(每题3分,共30分)
1.已知是方程的解,则的值是( )
A. B. C. D.
2.下列式子中,是二元一次方程组的是( ).
A. B. C. D.
3.若是关于x、y的方程2x+ay=6的解,则a的值为( )
A.1 B.2 C.3 D.4
4.二元一次方程3x+y=8的正整数解有( )
A.2个 B.3个 C.4个 D.5个
5.已知是二元一次方程组的解,则代数式的值为( )
A. B. C. D.
6.如果,则、的值分别是( )
A. B. C. D.
7.若和是方程的两组解,则m,n的值分别为( )
A., B.2,4 C.4,2 D.,
8.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9. 小明要用40元钱购买A,B两种型号的口罩,两种型号的口罩必须都购买,且40元钱全部用尽.若每个A型口
罩6元,每个B型口罩4元,则小明的购买方案有( )
A. 2种 B. 3种 C. 4种 D. 5种
10. 某出租车起步价所包含的路程为0~2km,超过2km的部分按每千米另收费.津津乘坐这种出租车走了7km,付了16元;盼盼乘坐这种出租车走了13km,付了28元.设这种出租车的起步价为x元,超过2km后每千米收费y元,则下列方程正确的是( )
A. B.
C. D.
二、填空题(每题3分,共24分)
11.已知,请用含的代数式表示,则____.
12.已知是方程的解,则__________
13.若是关于,的二元一次方程,则的值是______.
14.已知方程组的解为,则的值为__________.
15.已知是方程3mx﹣y=﹣1的解,则m=_____.
16.若关于的二元一次方程组的解是互为相反数,则的值是_________.
17.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的两根铁棒长度之和为,此时木桶中水的深度是________.
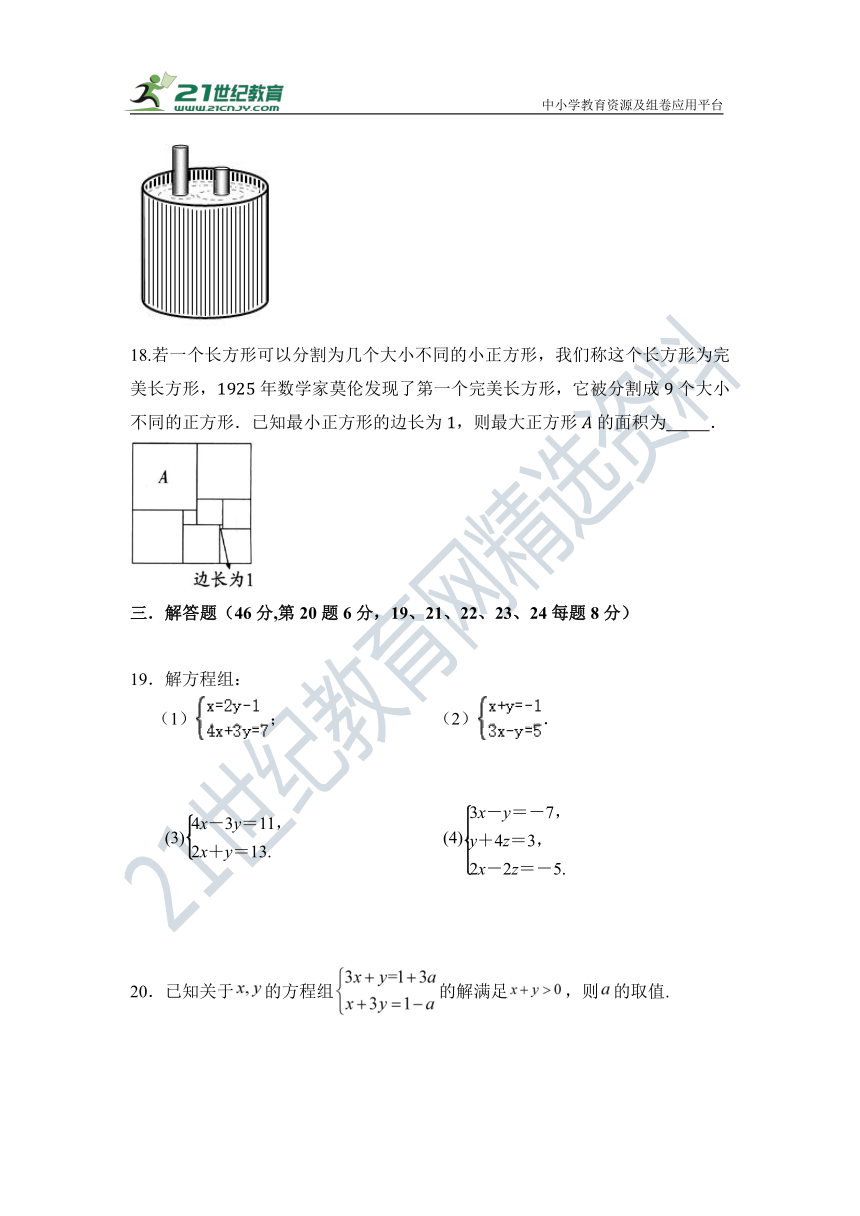
18.若一个长方形可以分割为几个大小不同的小正方形,我们称这个长方形为完美长方形,年数学家莫伦发现了第一个完美长方形,它被分割成个大小不同的正方形.已知最小正方形的边长为,则最大正方形的面积为 .
三.解答题(46分,第20题6分,19、21、22、23、24每题8分)
19.解方程组:
(1); (2).
(3) (4)
20.已知关于的方程组的解满足,则的取值.
21.已知关于,的方程组
(1)请直接写出方程的所有正整数解;
(2)若方程组的解满足,求的值;
(3)无论实数取何值,方程总有一个公共解,请直接写出这个公共解.
22.如图,在长为10米,宽为8米的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.
23.用二元一次方程组解决问题:近日由于城市地下水管老旧破裂,全市停水.小明去超市购买生活用水,已知大桶矿泉水每桶5升,价值10.5元,小瓶矿泉水每瓶500毫升,价值1.5元.(1升=1000毫升)
(1)若小明要购买1大桶矿泉水和3小瓶矿泉水,需要 元;
(2)若小明生活用水总量为20升,共花费46.5元,问这两种矿泉水各买多少?
24.随着“互联网+”时代的到来,一种新型的打车方式颇受欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按元/来计算,耗时费按元/分钟计算(总费用不足元按元计价),甲,乙两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程和平均车速见表:
平均车速 里程 车费(元)
甲
乙
(1)求的值;
(2)星期日,王老师也用该打车方式行驶了,若平均车速为,求王老师这次打车的总费用.
【答案】
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B A D B C B A C
二、填空题:
11.【答案】
【解析】解:由,移项可得.
本题由,直接移项可得.
本题主要考查二元一次方程的变形,解题的关键是熟练掌握解二元一次方程的基本步骤.
12.【答案】
【解析】【分析】
此题考查一元一次方程的解法和方程的解,解题关键是把方程的解代入原方程,使原方程转化为以系数为未知数的一元一次方程,再求解.知道了方程的解,可以把这对数值代入方程,得到一个含有未知数的一元一次方程,从而可以求出的值.
【解答】
解:把代入方程,得,解得.
故答案为.
13.【答案】
14.6
15.
16.9
17.【答案】
18.【答案】
三.解答题
19.解:(1)
,
把①代入②得:4(2y﹣1)+3y=7,
解得:y=1,
把y=1代入①得:x=1,
则方程组的解为;
(2)
,
①+②得:4x=4,
解得:x=1,
把x=1代入①得:y=﹣2,
则方程组的解为.
(3)
①+②×3,得10x=50,
解得x=5.
把x=5代入②,
得2×5+y=13,解得y=3.
于是,得方程组的解为
(4)
①+②得3x+4z=-4.④
④+③×2得x=-2.
把x=-2代入①得y=1.
把x=-2代入③得z=.
所以
20.a> 1
21.(1);(2);(3).
22. 8
【解析】
设小长方形的长为 x 米,宽为y米. 依题意有:解方程组即可.
解: 设小长方形的长为 x 米,宽为y米.
依题意有:
解此方程组得:
故,小长方形的长为 4米,宽为2米.
23.(1)15;(2)
24.(1);(2)王老师这次打车的总费用为元
【解析】
(1)先求解甲同学行驶时间为.乙同学行驶时间为.再根据相等关系列方程组,解方程组可得答案;
(2)先求解王老师该次打车行驶时间,再列式计算即可.
解:(1)甲同学行驶里程为,时间为.
乙同学行驶里程为,时间为.
由题意得:,
解得,
(2)王老师该次打车行驶时间为.
答:王老师这次打车的总费用为元.
第八章《二元一次方程组》单元检测题
一、选择题(每题3分,共30分)
1.已知是方程的解,则的值是( )
A. B. C. D.
2.下列式子中,是二元一次方程组的是( ).
A. B. C. D.
3.若是关于x、y的方程2x+ay=6的解,则a的值为( )
A.1 B.2 C.3 D.4
4.二元一次方程3x+y=8的正整数解有( )
A.2个 B.3个 C.4个 D.5个
5.已知是二元一次方程组的解,则代数式的值为( )
A. B. C. D.
6.如果,则、的值分别是( )
A. B. C. D.
7.若和是方程的两组解,则m,n的值分别为( )
A., B.2,4 C.4,2 D.,
8.以方程组的解为坐标的点(x,y)在平面直角坐标系中的位置是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
9. 小明要用40元钱购买A,B两种型号的口罩,两种型号的口罩必须都购买,且40元钱全部用尽.若每个A型口
罩6元,每个B型口罩4元,则小明的购买方案有( )
A. 2种 B. 3种 C. 4种 D. 5种
10. 某出租车起步价所包含的路程为0~2km,超过2km的部分按每千米另收费.津津乘坐这种出租车走了7km,付了16元;盼盼乘坐这种出租车走了13km,付了28元.设这种出租车的起步价为x元,超过2km后每千米收费y元,则下列方程正确的是( )
A. B.
C. D.
二、填空题(每题3分,共24分)
11.已知,请用含的代数式表示,则____.
12.已知是方程的解,则__________
13.若是关于,的二元一次方程,则的值是______.
14.已知方程组的解为,则的值为__________.
15.已知是方程3mx﹣y=﹣1的解,则m=_____.
16.若关于的二元一次方程组的解是互为相反数,则的值是_________.
17.如图,两根铁棒直立于桶底水平的木桶中,在桶中加入水后,一根露出水面的长度是它的,另一根露出水面的长度是它的两根铁棒长度之和为,此时木桶中水的深度是________.
18.若一个长方形可以分割为几个大小不同的小正方形,我们称这个长方形为完美长方形,年数学家莫伦发现了第一个完美长方形,它被分割成个大小不同的正方形.已知最小正方形的边长为,则最大正方形的面积为 .
三.解答题(46分,第20题6分,19、21、22、23、24每题8分)
19.解方程组:
(1); (2).
(3) (4)
20.已知关于的方程组的解满足,则的取值.
21.已知关于,的方程组
(1)请直接写出方程的所有正整数解;
(2)若方程组的解满足,求的值;
(3)无论实数取何值,方程总有一个公共解,请直接写出这个公共解.
22.如图,在长为10米,宽为8米的长方形空地上,沿平行于长方形边的方向分割出三个形状、大小完全一样的小长方形花圃(阴影部分).求其中一个小长方形的长和宽.
23.用二元一次方程组解决问题:近日由于城市地下水管老旧破裂,全市停水.小明去超市购买生活用水,已知大桶矿泉水每桶5升,价值10.5元,小瓶矿泉水每瓶500毫升,价值1.5元.(1升=1000毫升)
(1)若小明要购买1大桶矿泉水和3小瓶矿泉水,需要 元;
(2)若小明生活用水总量为20升,共花费46.5元,问这两种矿泉水各买多少?
24.随着“互联网+”时代的到来,一种新型的打车方式颇受欢迎,该打车方式的总费用由里程费和耗时费组成,其中里程费按元/来计算,耗时费按元/分钟计算(总费用不足元按元计价),甲,乙两人用该打车方式出行,按上述计价规则,其打车总费用、行驶里程和平均车速见表:
平均车速 里程 车费(元)
甲
乙
(1)求的值;
(2)星期日,王老师也用该打车方式行驶了,若平均车速为,求王老师这次打车的总费用.
【答案】
一、选择题:
题号 1 2 3 4 5 6 7 8 9 10
答案 A C B A D B C B A C
二、填空题:
11.【答案】
【解析】解:由,移项可得.
本题由,直接移项可得.
本题主要考查二元一次方程的变形,解题的关键是熟练掌握解二元一次方程的基本步骤.
12.【答案】
【解析】【分析】
此题考查一元一次方程的解法和方程的解,解题关键是把方程的解代入原方程,使原方程转化为以系数为未知数的一元一次方程,再求解.知道了方程的解,可以把这对数值代入方程,得到一个含有未知数的一元一次方程,从而可以求出的值.
【解答】
解:把代入方程,得,解得.
故答案为.
13.【答案】
14.6
15.
16.9
17.【答案】
18.【答案】
三.解答题
19.解:(1)
,
把①代入②得:4(2y﹣1)+3y=7,
解得:y=1,
把y=1代入①得:x=1,
则方程组的解为;
(2)
,
①+②得:4x=4,
解得:x=1,
把x=1代入①得:y=﹣2,
则方程组的解为.
(3)
①+②×3,得10x=50,
解得x=5.
把x=5代入②,
得2×5+y=13,解得y=3.
于是,得方程组的解为
(4)
①+②得3x+4z=-4.④
④+③×2得x=-2.
把x=-2代入①得y=1.
把x=-2代入③得z=.
所以
20.a> 1
21.(1);(2);(3).
22. 8
【解析】
设小长方形的长为 x 米,宽为y米. 依题意有:解方程组即可.
解: 设小长方形的长为 x 米,宽为y米.
依题意有:
解此方程组得:
故,小长方形的长为 4米,宽为2米.
23.(1)15;(2)
24.(1);(2)王老师这次打车的总费用为元
【解析】
(1)先求解甲同学行驶时间为.乙同学行驶时间为.再根据相等关系列方程组,解方程组可得答案;
(2)先求解王老师该次打车行驶时间,再列式计算即可.
解:(1)甲同学行驶里程为,时间为.
乙同学行驶里程为,时间为.
由题意得:,
解得,
(2)王老师该次打车行驶时间为.
答:王老师这次打车的总费用为元.
