【北师大版九上同步练习】 第四章 图形的相似(能力提升)检测题(含答案)
文档属性
| 名称 | 【北师大版九上同步练习】 第四章 图形的相似(能力提升)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 18.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 15:10:44 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
【北师大版九上同步练习】
第四章图形的相似(能力提升)检测题
一、单选题
1. 已知2x=5y(y≠0),则下列比例式成立的是( )
A. = B. = C. = D.=
2.如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:①,②,③,④,⑤,使与一定相似的有( )
A.①②④ B.②④⑤ C.①②③④ D.①②③⑤
3.如图,直线,它们依次交直线m、n于点A、B、C和D、E、F,已知,那么EF等于( )
A.2 B.3 C.4 D.5
4.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
5.如果两个相似三角形的周长比为,那么它们的对应角平分线的比为( )
A. B. C. D.
二、填空题
6.已知,是方程的两个实数根,则的值是 .
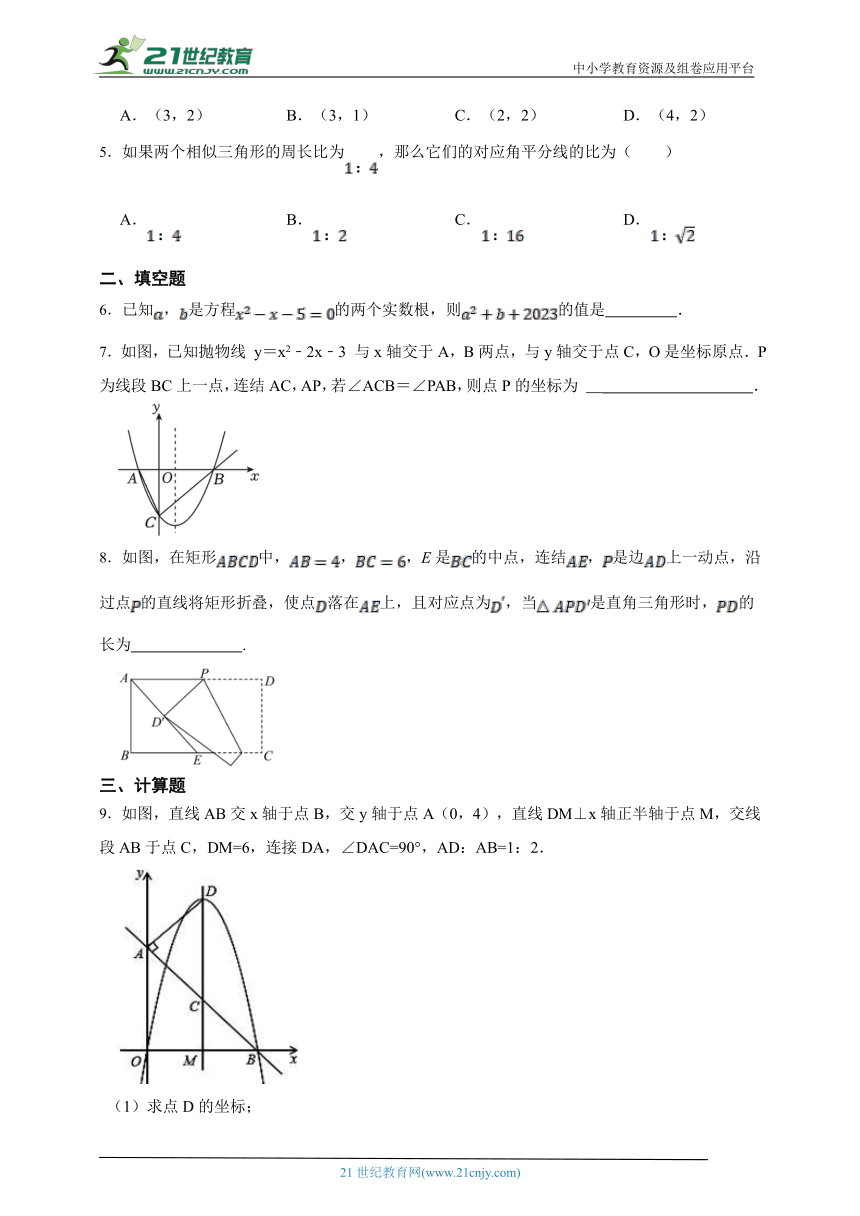
7.如图,已知抛物线 y=x2﹣2x﹣3 与x轴交于A,B两点,与y轴交于点C,O是坐标原点.P为线段BC上一点,连结AC,AP,若∠ACB=∠PAB,则点P的坐标为 .
8.如图,在矩形中,,,E是的中点,连结,是边上一动点,沿过点的直线将矩形折叠,使点落在上,且对应点为,当是直角三角形时,的长为 .
三、计算题
9.如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.
(1)求点D的坐标;
(2)求经过O、D、B三点的抛物线的函数关系式.
四、解答题
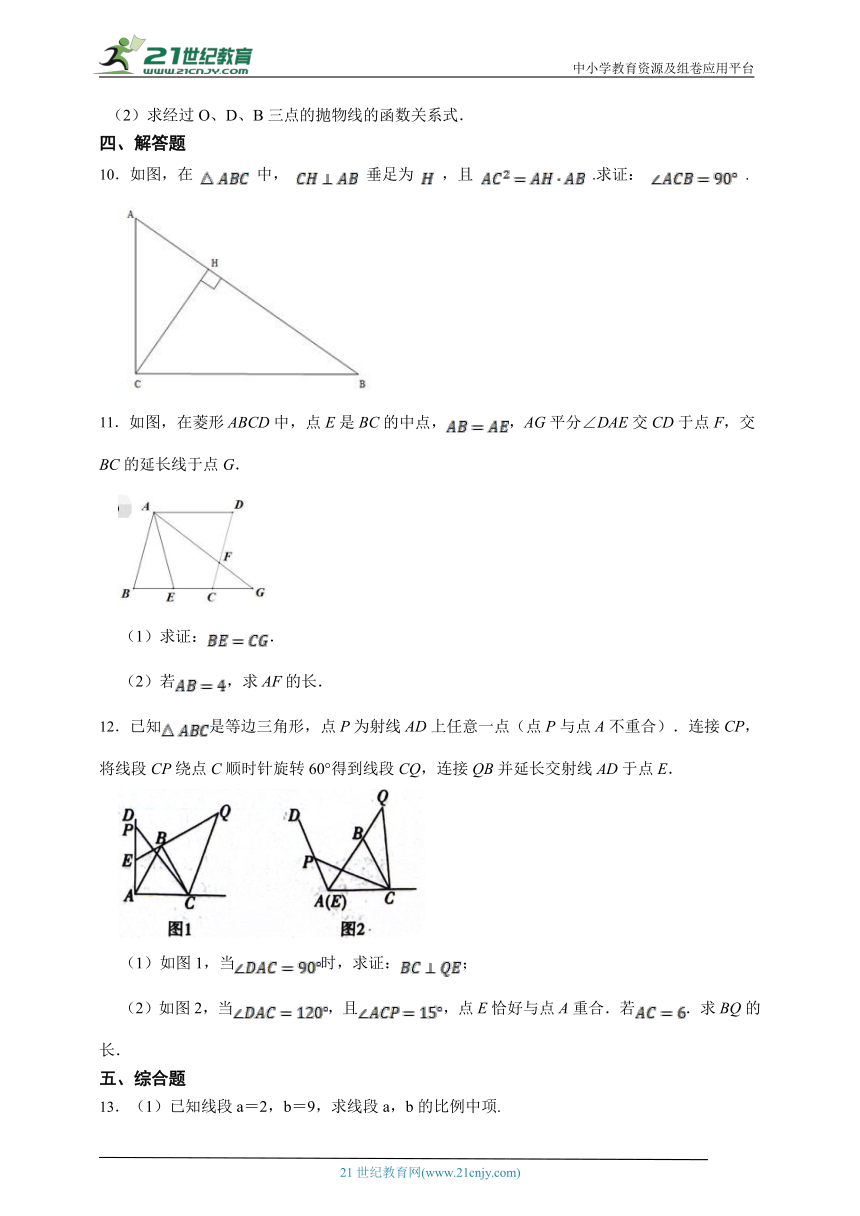
10.如图,在 中, 垂足为 ,且 .求证: .
11.如图,在菱形ABCD中,点E是BC的中点,,AG平分∠DAE交CD于点F,交BC的延长线于点G.
(1)求证:.
(2)若,求AF的长.
12.已知是等边三角形,点P为射线AD上任意一点(点P与点A不重合).连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连接QB并延长交射线AD于点E.
(1)如图1,当时,求证:;
(2)如图2,当,且,点E恰好与点A重合.若.求BQ的长.
五、综合题
13.(1)已知线段a=2,b=9,求线段a,b的比例中项.
(2)已知x:y=4:3,求的值.
14.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
15.在 中, , ,点 为边 的中点,以 为一边作正方形 ,
(1)如图1,点E恰好与点A重合,则线段BE与AF的数量关系为 ;
(2)在(1)的条件下,
①如果正方形 绕点 旋转,连接 、 、 ,线段 与AF的数量关系有无变化?请仅就图2的情形给出证明;
②正方形 绕点 旋转的过程中,当以点A,B,C,E为顶点的四边形是平行四边形时.直接写出线段AF的长.
六、实践探究题
16.综合与实践
(1)探究发现:如图1,在的网格图中,在线段上求一点P,使得;小明同学发现,先在点B的左侧取点C,使为1个单位长度,在点A的右侧取点D,使为2个单位长度,然后连接交于点P(如图1),就可以得到点P了,请你验证小明的做法,并求出的值.
(2)请你在图2中线段上求作一点P,使得.
17.
图1 图2 图3 图4
(1)问题提出:如图1,在正方形ABCD中,E,F分别为边DC,BC上的点,,连接EF,试说明线段DE,BF和EF之间的数量关系
小明是这样思考的:将绕点A按顺时针方向旋转得到(如图2),此时GF即是.直接写出线段DE,BF和EF之间的数量关系: .
(2)问题探究:如图3,在直角梯形ABCD中,(),,E是边CD上的一点.若,求BE的长.
(3)问题解决:某小区想在一块不规则的空地上修建一个花园,根据设计要求,花园由一个三角形和一个正方形组成,如图4所示.已知,以AB为边作正方形ADEB,现要在花园里修建一条小路CD,为了满足观赏需求,小路CD要尽可能长,求出此时的度数及小路CD的最大值.
18.探究与推理
如图1,在矩形中,,,连,点为上的一个动点,点从点出发,以每秒4个单位的速度沿向终点运动.过点作的平行线交于点,将沿对折,点落在点处,连交于点,设运动的时间为秒;
图1 图2 备用图
(1)用含有的式子表示.
(2)当为何值时,点恰好落在线段上;
(3)如图2,在点运动过程中,以为直径作,当为何值时,与矩形的边相切?请说明理由.
答案解析部分
1.【答案】D
【知识点】比例的性质
2.【答案】A
【知识点】相似三角形的判定
3.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】A
【知识点】位似变换
5.【答案】A
【知识点】相似三角形的性质
6.【答案】
【知识点】一元二次方程的根与系数的关系;求代数式的值-整体代入求值
7.【答案】(,﹣)
【知识点】坐标与图形性质;二次函数图象与坐标轴的交点问题;相似三角形的判定与性质
8.【答案】或
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题);相似三角形的判定与性质
9.【答案】(1)如图,过点D作DE⊥OA于E,
在△AED与△BAO中
∵∠EDA+∠EAD=∠EAD+∠BAO=90°,
∴∠EDA=∠BAO,
∵∠AED=∠AOB=90°,
∴△ADE∽△BAO,
∴
∵点A(0,4),DM=6,
∴AO=4,AE=EO-AO=DM-AO=2,
∴ED=,
∴点D的坐标为D(2,6).
(2)∵AE=2,ED=2,△ADE∽△BAO,
∴BO=AO=4
∴点B的坐标为B(4,0)
设:过O、D、B三点的抛物线的函数关系式为:
将O(0,0),B(0,4),D(2,6)代入函数关系式,解得:
∴过O、D、B三点的抛物线的函数关系式为:.
【知识点】坐标与图形性质;待定系数法求二次函数解析式;相似三角形的判定与性质
10.【答案】解:∵ ,
∴∠AHC=90°,
∵ ,即: ,
又∵∠A=∠A,
∴ ,
∴∠ACB=∠AHC=90°.
【知识点】相似三角形的判定与性质
11.【答案】(1)证明:∵四边形ABCD是菱形,
∴AB=BC,AD∥BC.
∴∠DAG=∠G.
∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠G=∠EAG,∴AE=EG
∵AB=AE=BC
∴BC=EG
∴BE=CG-
(2)解:过点A作AH⊥BE,垂足为点H.则BH=HE
∵点E是BC的中点,AB=4,
∴BE=EC=CG=2,BH=HE=1.
∵∠AHE=90°,
∴AH=,AG=.
∵AD∥BC,
∴△ABC∽△DEF,∴,∴AF=.
【知识点】勾股定理;菱形的性质;相似三角形的判定与性质
12.【答案】(1)证明:如图1,QE与CP的交点记为M,
∵,且,
在和中,,
∴,∴,
∵,∴,∴.
(2)解:如图2,作于H,
与(1)一样可证明,∴,
∵,,
∴,,∴,
∴为等腰直角三角形,∴,,
在中,,
∴,∴.
【知识点】等边三角形的性质;旋转的性质
13.【答案】(1)解:设线段x是线段a,b的比例中项,
∵a=3,b=6,
x2=3×6=18,
x=(负值舍去).
∴线段a,b的比例中项是3.
(2)解:设x=4k,y=3k,
∴==.
【知识点】比例的性质;比例线段
14.【答案】(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,
∴EF= =13,
∴OC= EF=6.5
(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
【知识点】平行线的性质;等腰三角形的判定与性质;矩形的判定;直角三角形斜边上的中线
15.【答案】(1)
(2)解:①无变化
理由如下:在 中,
∵
∴
∴
在正方形 中,
在 中,
∴
∵
∴
∴
∴
∴
∴
∴线段 与 的数量关系无变化
②如图,当点F在BC 边上时,
此时,点F是BC边的中点,
∵△ABC是等腰直角三角形,AB=BC=3
∴
∴
如图,当点F在BC边的延长线上时,过点A作AG⊥BC于点G,
由①知,AG=CD=CG=CF=
在Rt△AGF中,AG= ,GF=GC+CF=+ + =
∴AF=
综上,线段AF的长为 或 .
【知识点】正方形的性质;相似三角形的判定与性质;解直角三角形;旋转的性质;等腰直角三角形
16.【答案】(1)解:∵
∴,
∴
∴
连接
∵
∴
∴
∵,,
∴
∴是直角三角形
∴
∴
(2)解:如图所示,点P就是所求作的点
【知识点】相似三角形的判定与性质;尺规作图-直线、射线、线段;解直角三角形—三边关系(勾股定理)
17.【答案】(1)
(2)如图,过点A作,交CB的延长线于点F.
,
,
∴四边形AFCD是矩形
,
∴四边形AFCD是正方形,
.
根据上面结论,可知.
设,
,
.
,
,
解得,即.
(3)如图,过点A作,取,连接BF,CF. 7分
,
.
又,
,
,
∴当线段CD有最大值时,只需BF最大即可.
,
∴当B,C,F三点共线时,BF取得最大值,此时.
在等腰直角中,,
.
,
∴BF的最大值为,此时,
∴CD的最大值为.
【知识点】勾股定理;正方形的判定与性质;旋转的性质;三角形全等的判定-SAS
18.【答案】(1)解:依题可知,由折叠可知
在矩形中,,,
又
.
(2)解:(法一)由折叠可知垂直平分
点恰好落在线段上,
,
(法二)由折叠可知
又,,
(3)解:连接
依题可知,为的中点,为的中点,,,即半径为
在矩形中,
又,,
,
①当与边相切于时,如图①所示
图①
连接,
又
、、三点共线
过作于
四边形为矩形,
解得
②当与边相切于时,如图②所示
图②
连接,并延长交于,,
四边形为矩形,,
又,,四边形为矩形
解得
综上所述,或
【知识点】勾股定理;矩形的判定与性质;圆的综合题;翻折变换(折叠问题);锐角三角函数的定义
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版九上同步练习】
第四章图形的相似(能力提升)检测题
一、单选题
1. 已知2x=5y(y≠0),则下列比例式成立的是( )
A. = B. = C. = D.=
2.如图,点D,E分别在的AB,AC边上,增加下列条件中的一个:①,②,③,④,⑤,使与一定相似的有( )
A.①②④ B.②④⑤ C.①②③④ D.①②③⑤
3.如图,直线,它们依次交直线m、n于点A、B、C和D、E、F,已知,那么EF等于( )
A.2 B.3 C.4 D.5
4.如图,在平面直角坐标中,正方形ABCD与正方形BEFG是以原点O为位似中心的位似图形,且相似比为 ,点A,B,E在x轴上,若正方形BEFG的边长为6,则C点坐标为( )
A.(3,2) B.(3,1) C.(2,2) D.(4,2)
5.如果两个相似三角形的周长比为,那么它们的对应角平分线的比为( )
A. B. C. D.
二、填空题
6.已知,是方程的两个实数根,则的值是 .
7.如图,已知抛物线 y=x2﹣2x﹣3 与x轴交于A,B两点,与y轴交于点C,O是坐标原点.P为线段BC上一点,连结AC,AP,若∠ACB=∠PAB,则点P的坐标为 .
8.如图,在矩形中,,,E是的中点,连结,是边上一动点,沿过点的直线将矩形折叠,使点落在上,且对应点为,当是直角三角形时,的长为 .
三、计算题
9.如图,直线AB交x轴于点B,交y轴于点A(0,4),直线DM⊥x轴正半轴于点M,交线段AB于点C,DM=6,连接DA,∠DAC=90°,AD:AB=1:2.
(1)求点D的坐标;
(2)求经过O、D、B三点的抛物线的函数关系式.
四、解答题
10.如图,在 中, 垂足为 ,且 .求证: .
11.如图,在菱形ABCD中,点E是BC的中点,,AG平分∠DAE交CD于点F,交BC的延长线于点G.
(1)求证:.
(2)若,求AF的长.
12.已知是等边三角形,点P为射线AD上任意一点(点P与点A不重合).连接CP,将线段CP绕点C顺时针旋转60°得到线段CQ,连接QB并延长交射线AD于点E.
(1)如图1,当时,求证:;
(2)如图2,当,且,点E恰好与点A重合.若.求BQ的长.
五、综合题
13.(1)已知线段a=2,b=9,求线段a,b的比例中项.
(2)已知x:y=4:3,求的值.
14.如图,△ABC中,点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
15.在 中, , ,点 为边 的中点,以 为一边作正方形 ,
(1)如图1,点E恰好与点A重合,则线段BE与AF的数量关系为 ;
(2)在(1)的条件下,
①如果正方形 绕点 旋转,连接 、 、 ,线段 与AF的数量关系有无变化?请仅就图2的情形给出证明;
②正方形 绕点 旋转的过程中,当以点A,B,C,E为顶点的四边形是平行四边形时.直接写出线段AF的长.
六、实践探究题
16.综合与实践
(1)探究发现:如图1,在的网格图中,在线段上求一点P,使得;小明同学发现,先在点B的左侧取点C,使为1个单位长度,在点A的右侧取点D,使为2个单位长度,然后连接交于点P(如图1),就可以得到点P了,请你验证小明的做法,并求出的值.
(2)请你在图2中线段上求作一点P,使得.
17.
图1 图2 图3 图4
(1)问题提出:如图1,在正方形ABCD中,E,F分别为边DC,BC上的点,,连接EF,试说明线段DE,BF和EF之间的数量关系
小明是这样思考的:将绕点A按顺时针方向旋转得到(如图2),此时GF即是.直接写出线段DE,BF和EF之间的数量关系: .
(2)问题探究:如图3,在直角梯形ABCD中,(),,E是边CD上的一点.若,求BE的长.
(3)问题解决:某小区想在一块不规则的空地上修建一个花园,根据设计要求,花园由一个三角形和一个正方形组成,如图4所示.已知,以AB为边作正方形ADEB,现要在花园里修建一条小路CD,为了满足观赏需求,小路CD要尽可能长,求出此时的度数及小路CD的最大值.
18.探究与推理
如图1,在矩形中,,,连,点为上的一个动点,点从点出发,以每秒4个单位的速度沿向终点运动.过点作的平行线交于点,将沿对折,点落在点处,连交于点,设运动的时间为秒;
图1 图2 备用图
(1)用含有的式子表示.
(2)当为何值时,点恰好落在线段上;
(3)如图2,在点运动过程中,以为直径作,当为何值时,与矩形的边相切?请说明理由.
答案解析部分
1.【答案】D
【知识点】比例的性质
2.【答案】A
【知识点】相似三角形的判定
3.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】A
【知识点】位似变换
5.【答案】A
【知识点】相似三角形的性质
6.【答案】
【知识点】一元二次方程的根与系数的关系;求代数式的值-整体代入求值
7.【答案】(,﹣)
【知识点】坐标与图形性质;二次函数图象与坐标轴的交点问题;相似三角形的判定与性质
8.【答案】或
【知识点】勾股定理;矩形的性质;翻折变换(折叠问题);相似三角形的判定与性质
9.【答案】(1)如图,过点D作DE⊥OA于E,
在△AED与△BAO中
∵∠EDA+∠EAD=∠EAD+∠BAO=90°,
∴∠EDA=∠BAO,
∵∠AED=∠AOB=90°,
∴△ADE∽△BAO,
∴
∵点A(0,4),DM=6,
∴AO=4,AE=EO-AO=DM-AO=2,
∴ED=,
∴点D的坐标为D(2,6).
(2)∵AE=2,ED=2,△ADE∽△BAO,
∴BO=AO=4
∴点B的坐标为B(4,0)
设:过O、D、B三点的抛物线的函数关系式为:
将O(0,0),B(0,4),D(2,6)代入函数关系式,解得:
∴过O、D、B三点的抛物线的函数关系式为:.
【知识点】坐标与图形性质;待定系数法求二次函数解析式;相似三角形的判定与性质
10.【答案】解:∵ ,
∴∠AHC=90°,
∵ ,即: ,
又∵∠A=∠A,
∴ ,
∴∠ACB=∠AHC=90°.
【知识点】相似三角形的判定与性质
11.【答案】(1)证明:∵四边形ABCD是菱形,
∴AB=BC,AD∥BC.
∴∠DAG=∠G.
∵AG平分∠DAE,
∴∠DAG=∠EAG,
∴∠G=∠EAG,∴AE=EG
∵AB=AE=BC
∴BC=EG
∴BE=CG-
(2)解:过点A作AH⊥BE,垂足为点H.则BH=HE
∵点E是BC的中点,AB=4,
∴BE=EC=CG=2,BH=HE=1.
∵∠AHE=90°,
∴AH=,AG=.
∵AD∥BC,
∴△ABC∽△DEF,∴,∴AF=.
【知识点】勾股定理;菱形的性质;相似三角形的判定与性质
12.【答案】(1)证明:如图1,QE与CP的交点记为M,
∵,且,
在和中,,
∴,∴,
∵,∴,∴.
(2)解:如图2,作于H,
与(1)一样可证明,∴,
∵,,
∴,,∴,
∴为等腰直角三角形,∴,,
在中,,
∴,∴.
【知识点】等边三角形的性质;旋转的性质
13.【答案】(1)解:设线段x是线段a,b的比例中项,
∵a=3,b=6,
x2=3×6=18,
x=(负值舍去).
∴线段a,b的比例中项是3.
(2)解:设x=4k,y=3k,
∴==.
【知识点】比例的性质;比例线段
14.【答案】(1)证明:∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,∠4=∠6,
∵MN∥BC,
∴∠1=∠5,∠3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF
(2)解:∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,
∴EF= =13,
∴OC= EF=6.5
(3)解:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
【知识点】平行线的性质;等腰三角形的判定与性质;矩形的判定;直角三角形斜边上的中线
15.【答案】(1)
(2)解:①无变化
理由如下:在 中,
∵
∴
∴
在正方形 中,
在 中,
∴
∵
∴
∴
∴
∴
∴
∴线段 与 的数量关系无变化
②如图,当点F在BC 边上时,
此时,点F是BC边的中点,
∵△ABC是等腰直角三角形,AB=BC=3
∴
∴
如图,当点F在BC边的延长线上时,过点A作AG⊥BC于点G,
由①知,AG=CD=CG=CF=
在Rt△AGF中,AG= ,GF=GC+CF=+ + =
∴AF=
综上,线段AF的长为 或 .
【知识点】正方形的性质;相似三角形的判定与性质;解直角三角形;旋转的性质;等腰直角三角形
16.【答案】(1)解:∵
∴,
∴
∴
连接
∵
∴
∴
∵,,
∴
∴是直角三角形
∴
∴
(2)解:如图所示,点P就是所求作的点
【知识点】相似三角形的判定与性质;尺规作图-直线、射线、线段;解直角三角形—三边关系(勾股定理)
17.【答案】(1)
(2)如图,过点A作,交CB的延长线于点F.
,
,
∴四边形AFCD是矩形
,
∴四边形AFCD是正方形,
.
根据上面结论,可知.
设,
,
.
,
,
解得,即.
(3)如图,过点A作,取,连接BF,CF. 7分
,
.
又,
,
,
∴当线段CD有最大值时,只需BF最大即可.
,
∴当B,C,F三点共线时,BF取得最大值,此时.
在等腰直角中,,
.
,
∴BF的最大值为,此时,
∴CD的最大值为.
【知识点】勾股定理;正方形的判定与性质;旋转的性质;三角形全等的判定-SAS
18.【答案】(1)解:依题可知,由折叠可知
在矩形中,,,
又
.
(2)解:(法一)由折叠可知垂直平分
点恰好落在线段上,
,
(法二)由折叠可知
又,,
(3)解:连接
依题可知,为的中点,为的中点,,,即半径为
在矩形中,
又,,
,
①当与边相切于时,如图①所示
图①
连接,
又
、、三点共线
过作于
四边形为矩形,
解得
②当与边相切于时,如图②所示
图②
连接,并延长交于,,
四边形为矩形,,
又,,四边形为矩形
解得
综上所述,或
【知识点】勾股定理;矩形的判定与性质;圆的综合题;翻折变换(折叠问题);锐角三角函数的定义
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
