【北师大版九上同步练习】 第四章 图形的相似(培优)检测题(含答案)
文档属性
| 名称 | 【北师大版九上同步练习】 第四章 图形的相似(培优)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 27.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 15:12:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【北师大版九上同步练习】
第四章图形的相似(培优)检测题
一、单选题
1.已知,则下列各式成立的是( )
A. B. C. D.
2.如图,能使∽成立的条件是( )
A. B. C. D.
3.如图,已知,它们依次交直线于点A、B、C和点D、E、F,如果,那么的长等于( )
A.2 B.4 C. D.
4.如图,在平面直角坐标系中,的顶点为,,.以点为位似中心,在第三象限内作与的位似比为的位似图形,则点的坐标为( )
A. B. C. D.
5.已知轴上有点,轴上有点,直线交轴的正半轴于点,交轴于点,若与相似(点O是坐标原点),则的值为( )
A. B. C.或2 D.或
二、填空题
6.设是关于x的方程x2-12x+1=0的两个根,则 .
7.如图,在中,对角线,BD交于点O,,于点,若AB=2,,则的长为 .
8.如图,在中,,,分别为,上的动点,,分别以,所在直线为对称轴翻折,,点,的对称点分别为,若、、、恰好在同一直线上,,且,则的长是 .
三、计算题
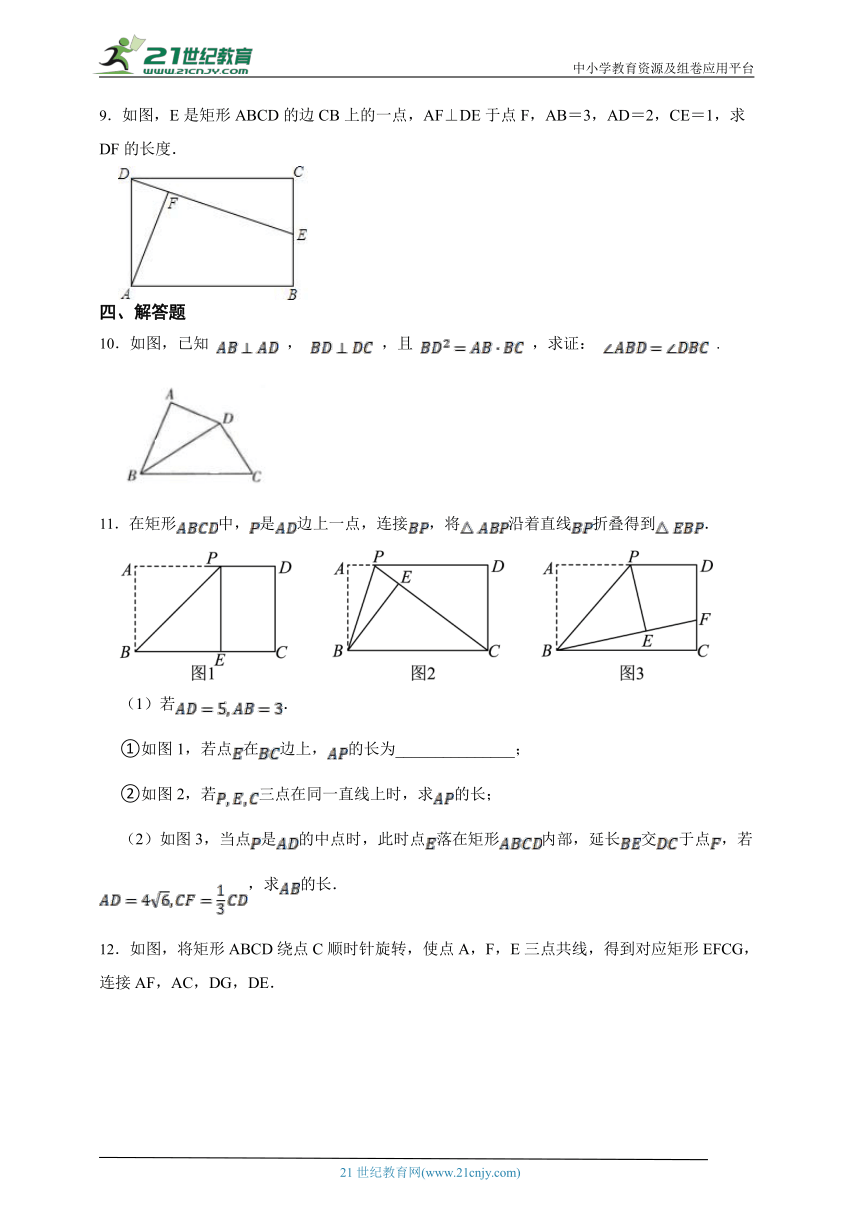
9.如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,求DF的长度.
四、解答题
10.如图,已知 , ,且 ,求证: .
11.在矩形中,是边上一点,连接,将沿着直线折叠得到.
(1)若.
①如图1,若点在边上,的长为_______________;
②如图2,若三点在同一直线上时,求的长;
(2)如图3,当点是的中点时,此时点落在矩形内部,延长交于点,若,求的长.
12.如图,将矩形ABCD绕点C顺时针旋转,使点A,F,E三点共线,得到对应矩形EFCG,连接AF,AC,DG,DE.
(1)求证:AF=CG;
(2)判断DG与AC的位置关系,并说明理由;
(3)若AB=3,BC=4,求tan∠AED的值.
五、综合题
13.如图,在 中, , , ,且 .
(1)求 的长;
(2)求证: .
14.如图,在菱形中,对角线,交于点,过点作的垂线,垂足为点,延长到点,使,连接.
(1)求证:四边形是矩形;
(2)连接,若,,求的长.
15.抛物线过点,点,顶点为,与轴相交于点,点是该抛物线上一动点,设点的横坐标为
(1)求抛物线的表达式.
(2)如图,连接,,,若的面积为,求的值;
(3)连接,过点作于点,是否存在点,使得,如果存在,请求出点的坐标;如果不存在,请说明理由.
六、实践探究题
16.【教材呈现】华师版九年级上册63页例1.
如图,在△ABC中,点D是边AB的三等分点,DE∥BC,DE=5,求BC的长.
【应用拓展】
(1)如图①,在△ABC中,点D是边AB的中点,点F为BC延长线上一点,连接DF交AC于点E,若DE:EF=3:1,DG∥AC,EC=2,则AC的长为 .
(2)如图②,在△ABC中,点D为边BA延长线上一点,点E为BC上一点,连接DE交AC于点F,若点A为DB的中点,CE:EB=1:2,△DBE的面积为4,则△CFE(阴影部分)面积为 .
17.为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽做了如下尝试:如图1,在中,是边上的中线,延长到点M,使,连接.
图1 图2 图3
(1)【探究发现】图1中与的数量关系是 ,位置关系是 ;
(2)【初步应用】如图2,在中,是边上的中线,若,,,判断的形状;
(3)【探究提升】如图3,在中,若,,D为边上的点,且,求的取值范围.
18.综合与实践:
综合与实践课上,高老师让同学们以“正方形的折叠”为主题开展数学活动.
【操作判断】
操作一:如图1,正方形纸片,将沿过点的直线折叠,使点落在正方形的内部,得到折痕,点的对应点为,连接;再将沿过点的直线折叠,使与重合,得到折痕,将纸片展平,连接.根据以上操作,同学们很快发现,,三点共线,且有以下结论:①;②线段,,之间的数量关系为:.
【深入探究】
操作二:如图2,再将沿所在直线折叠,使点落在正方形的内部,点的对应点为,将纸片展平,连接、.同学们在折纸的过程中发现,当点的位置不同时,点的位置也不同,在这次综合实践探究学习中,两位同学又有如下发现:
一、小曾发现,当点落在折痕上时,设交于点,如图2,则有结论:;
二、小段发现,当点落在折痕上时,是一个定值.
【解决问题】
(1)证明小曾同学结论的正确性:;
(2)小段同学的发现是否成立?若成立,求出的大小;若不成立,请说明理由.
(3)【拓展应用】
如图3,矩形中,,,点、分别在边、上,,,求的长度.
答案解析部分
1.【答案】D
【知识点】比例的性质
2.【答案】C
【知识点】相似三角形的判定
3.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】B
【知识点】位似变换
5.【答案】D
【知识点】相似三角形的性质
6.【答案】11
【知识点】一元二次方程的根与系数的关系
7.【答案】
【知识点】平行四边形的性质;相似三角形的判定与性质
8.【答案】7
【知识点】勾股定理;平行四边形的性质;翻折变换(折叠问题)
9.【答案】解:∵E是矩形ABCD的边CB上的一点
∴
∴
∵AF⊥DE
∴
∴ ,
∴
∴
∴
∵AB=3
∴
∵ ,CE=1
∴
∵AD=2
∴
∴ .
【知识点】相似三角形的判定与性质
10.【答案】解:∵
∴
∴Rt△ABD∽Rt△DBC
∴∠ABD=∠DBC
【知识点】相似三角形的判定与性质
11.【答案】(1)①3;②1
(2)6
【知识点】勾股定理;正方形的判定与性质
12.【答案】(1)证明:∵四边形ABCD,EFCG是矩形
∴AB=CD,∠B=90°,∠CFE=90°.
∴∠CFA=180°-∠CFE=90°.
由旋转的性质可得:BC=FC,CG=CD∴AB=CG
在Rt△ABC和Rt△AFC中,
∴Rt△ABC≌Rt△AFC(HL).
∴AF=AB,∴AF=CG.
(2)解:.理由如下:
连接DF,∵四边形ABCD是矩形,∴,∠DAC=∠BCA.
∵Rt△ABC≌Rt△AFC,∴∠FCA=∠BCA.∴∠DAC=∠FCA.
∴OA=OC,∵AD=FC∴OD=OF∴∠ODF=∠OFD.
∵∠AOC=∠DOF∴∠DAC=∠ODF.∴.
∵AF=CG,,∴四边形ACGF是平行四边形∴.
∴F,D,G三点共线.∴.
(3)解:过点C作CK⊥FG于点K,延长ED交CF于点H
∵CG=AB=3,CF=BC=4,∴
∵,∴
∴.
∵CD=CG,CK⊥FG,∴
∴.
∵,∴∠DFH=∠DGE,∠DHF=∠DEG.
∴,∴∴.
∴.
【知识点】平行线的判定;直角三角形全等的判定-HL;矩形的性质;相似三角形的判定与性质;旋转的性质
13.【答案】(1)解:设 ,则
∵ ,
∴
解得
∴ ;
(2)证明:∵ ,
∴
即 .
∴ .
【知识点】比例的性质;两条直线被一组平行线所截,所得的对应线段成比例
14.【答案】(1)证明:∵四边形是菱形,
∴,,
∵,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是矩形.
(2)解:∵四边形是菱形,是菱形的对角线,
∴,点是的中点,
∵是直角三角形,
∴,
∴,
∵,
∴,
解得:,
∴,
∴.
【知识点】勾股定理;菱形的性质;矩形的判定与性质;直角三角形斜边上的中线
15.【答案】(1)解:将点,点代入得:
,
解得.
抛物线的表达式为;
(2)解:,令,则,
点,
设直线的解析式为,
点,
,
解得.
直线解析式为,
过点作轴交于点,
设点,点,
,
的面积为,
,
,,
的值为或,
,
的值为;
(3)解:存在点,使得;理由如下:
在中,,
,
设交轴于点,延长交轴于,连接,过点作轴于点,如图,
,
顶点,
,
,,
,,.
,.
在中,,,
,
,
,
是等腰三角形,
,,
,
,为的中点,
是等腰三角形,,
,
,
∽,
,
,
.
,
设直线的解析式为,
,
解得.
直线的解析式为.
,
解得,,
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;相似三角形的判定与性质;二次函数-动态几何问题;数学思想
16.【答案】(1)16
(2)
【知识点】两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
17.【答案】(1);
(2)解:如图1,延长至点,使,连接.
图1
由(1)可知,,
,,,.
,,,
,.
,
,
,
,
为直角三角形.
(3)解:如图2,延长至点,使,连接,
图2
.
又,
,
.
,,
.
在中,由三角形三边关系可得,
即,
.
【知识点】三角形三边关系;勾股定理的逆定理;相似三角形的判定与性质;三角形全等的判定-SAS
18.【答案】(1)解:∵四边形是正方形,
∴.
由折叠的性质可知,,,
∴,
又∵,
∴.
由操作一知,
∴是等腰直角三角形,
∴N,
∴,
∴.
∵,
∴.
(2)解:成立,理由如下:
由折叠的性质可知,.
∵是等腰直角三角形,
∴,
∴.
∵,
∴,
∴.
∵,
∴,
∴.
(3)解:将三角形沿翻折,使点F落在点G处,连接交与点O,
∴,.
由折叠的性质得,
∴,
∴是等腰直角三角形,
∴,
∴.
∵四边形是矩形,
∴,,
∴,
∴.
设,则,
∴,.
在中,,
∵,
∴,
整理得,
∴或(舍去),
即.
【知识点】勾股定理;矩形的性质;正方形的性质;翻折变换(折叠问题);三角形全等的判定-ASA
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版九上同步练习】
第四章图形的相似(培优)检测题
一、单选题
1.已知,则下列各式成立的是( )
A. B. C. D.
2.如图,能使∽成立的条件是( )
A. B. C. D.
3.如图,已知,它们依次交直线于点A、B、C和点D、E、F,如果,那么的长等于( )
A.2 B.4 C. D.
4.如图,在平面直角坐标系中,的顶点为,,.以点为位似中心,在第三象限内作与的位似比为的位似图形,则点的坐标为( )
A. B. C. D.
5.已知轴上有点,轴上有点,直线交轴的正半轴于点,交轴于点,若与相似(点O是坐标原点),则的值为( )
A. B. C.或2 D.或
二、填空题
6.设是关于x的方程x2-12x+1=0的两个根,则 .
7.如图,在中,对角线,BD交于点O,,于点,若AB=2,,则的长为 .
8.如图,在中,,,分别为,上的动点,,分别以,所在直线为对称轴翻折,,点,的对称点分别为,若、、、恰好在同一直线上,,且,则的长是 .
三、计算题
9.如图,E是矩形ABCD的边CB上的一点,AF⊥DE于点F,AB=3,AD=2,CE=1,求DF的长度.
四、解答题
10.如图,已知 , ,且 ,求证: .
11.在矩形中,是边上一点,连接,将沿着直线折叠得到.
(1)若.
①如图1,若点在边上,的长为_______________;
②如图2,若三点在同一直线上时,求的长;
(2)如图3,当点是的中点时,此时点落在矩形内部,延长交于点,若,求的长.
12.如图,将矩形ABCD绕点C顺时针旋转,使点A,F,E三点共线,得到对应矩形EFCG,连接AF,AC,DG,DE.
(1)求证:AF=CG;
(2)判断DG与AC的位置关系,并说明理由;
(3)若AB=3,BC=4,求tan∠AED的值.
五、综合题
13.如图,在 中, , , ,且 .
(1)求 的长;
(2)求证: .
14.如图,在菱形中,对角线,交于点,过点作的垂线,垂足为点,延长到点,使,连接.
(1)求证:四边形是矩形;
(2)连接,若,,求的长.
15.抛物线过点,点,顶点为,与轴相交于点,点是该抛物线上一动点,设点的横坐标为
(1)求抛物线的表达式.
(2)如图,连接,,,若的面积为,求的值;
(3)连接,过点作于点,是否存在点,使得,如果存在,请求出点的坐标;如果不存在,请说明理由.
六、实践探究题
16.【教材呈现】华师版九年级上册63页例1.
如图,在△ABC中,点D是边AB的三等分点,DE∥BC,DE=5,求BC的长.
【应用拓展】
(1)如图①,在△ABC中,点D是边AB的中点,点F为BC延长线上一点,连接DF交AC于点E,若DE:EF=3:1,DG∥AC,EC=2,则AC的长为 .
(2)如图②,在△ABC中,点D为边BA延长线上一点,点E为BC上一点,连接DE交AC于点F,若点A为DB的中点,CE:EB=1:2,△DBE的面积为4,则△CFE(阴影部分)面积为 .
17.为了进一步探究三角形中线的作用,数学兴趣小组合作交流时,小丽做了如下尝试:如图1,在中,是边上的中线,延长到点M,使,连接.
图1 图2 图3
(1)【探究发现】图1中与的数量关系是 ,位置关系是 ;
(2)【初步应用】如图2,在中,是边上的中线,若,,,判断的形状;
(3)【探究提升】如图3,在中,若,,D为边上的点,且,求的取值范围.
18.综合与实践:
综合与实践课上,高老师让同学们以“正方形的折叠”为主题开展数学活动.
【操作判断】
操作一:如图1,正方形纸片,将沿过点的直线折叠,使点落在正方形的内部,得到折痕,点的对应点为,连接;再将沿过点的直线折叠,使与重合,得到折痕,将纸片展平,连接.根据以上操作,同学们很快发现,,三点共线,且有以下结论:①;②线段,,之间的数量关系为:.
【深入探究】
操作二:如图2,再将沿所在直线折叠,使点落在正方形的内部,点的对应点为,将纸片展平,连接、.同学们在折纸的过程中发现,当点的位置不同时,点的位置也不同,在这次综合实践探究学习中,两位同学又有如下发现:
一、小曾发现,当点落在折痕上时,设交于点,如图2,则有结论:;
二、小段发现,当点落在折痕上时,是一个定值.
【解决问题】
(1)证明小曾同学结论的正确性:;
(2)小段同学的发现是否成立?若成立,求出的大小;若不成立,请说明理由.
(3)【拓展应用】
如图3,矩形中,,,点、分别在边、上,,,求的长度.
答案解析部分
1.【答案】D
【知识点】比例的性质
2.【答案】C
【知识点】相似三角形的判定
3.【答案】C
【知识点】两条直线被一组平行线所截,所得的对应线段成比例
4.【答案】B
【知识点】位似变换
5.【答案】D
【知识点】相似三角形的性质
6.【答案】11
【知识点】一元二次方程的根与系数的关系
7.【答案】
【知识点】平行四边形的性质;相似三角形的判定与性质
8.【答案】7
【知识点】勾股定理;平行四边形的性质;翻折变换(折叠问题)
9.【答案】解:∵E是矩形ABCD的边CB上的一点
∴
∴
∵AF⊥DE
∴
∴ ,
∴
∴
∴
∵AB=3
∴
∵ ,CE=1
∴
∵AD=2
∴
∴ .
【知识点】相似三角形的判定与性质
10.【答案】解:∵
∴
∴Rt△ABD∽Rt△DBC
∴∠ABD=∠DBC
【知识点】相似三角形的判定与性质
11.【答案】(1)①3;②1
(2)6
【知识点】勾股定理;正方形的判定与性质
12.【答案】(1)证明:∵四边形ABCD,EFCG是矩形
∴AB=CD,∠B=90°,∠CFE=90°.
∴∠CFA=180°-∠CFE=90°.
由旋转的性质可得:BC=FC,CG=CD∴AB=CG
在Rt△ABC和Rt△AFC中,
∴Rt△ABC≌Rt△AFC(HL).
∴AF=AB,∴AF=CG.
(2)解:.理由如下:
连接DF,∵四边形ABCD是矩形,∴,∠DAC=∠BCA.
∵Rt△ABC≌Rt△AFC,∴∠FCA=∠BCA.∴∠DAC=∠FCA.
∴OA=OC,∵AD=FC∴OD=OF∴∠ODF=∠OFD.
∵∠AOC=∠DOF∴∠DAC=∠ODF.∴.
∵AF=CG,,∴四边形ACGF是平行四边形∴.
∴F,D,G三点共线.∴.
(3)解:过点C作CK⊥FG于点K,延长ED交CF于点H
∵CG=AB=3,CF=BC=4,∴
∵,∴
∴.
∵CD=CG,CK⊥FG,∴
∴.
∵,∴∠DFH=∠DGE,∠DHF=∠DEG.
∴,∴∴.
∴.
【知识点】平行线的判定;直角三角形全等的判定-HL;矩形的性质;相似三角形的判定与性质;旋转的性质
13.【答案】(1)解:设 ,则
∵ ,
∴
解得
∴ ;
(2)证明:∵ ,
∴
即 .
∴ .
【知识点】比例的性质;两条直线被一组平行线所截,所得的对应线段成比例
14.【答案】(1)证明:∵四边形是菱形,
∴,,
∵,
∴,
∴,
∵,
∴四边形是平行四边形,
∵,
∴,
∴平行四边形是矩形.
(2)解:∵四边形是菱形,是菱形的对角线,
∴,点是的中点,
∵是直角三角形,
∴,
∴,
∵,
∴,
解得:,
∴,
∴.
【知识点】勾股定理;菱形的性质;矩形的判定与性质;直角三角形斜边上的中线
15.【答案】(1)解:将点,点代入得:
,
解得.
抛物线的表达式为;
(2)解:,令,则,
点,
设直线的解析式为,
点,
,
解得.
直线解析式为,
过点作轴交于点,
设点,点,
,
的面积为,
,
,,
的值为或,
,
的值为;
(3)解:存在点,使得;理由如下:
在中,,
,
设交轴于点,延长交轴于,连接,过点作轴于点,如图,
,
顶点,
,
,,
,,.
,.
在中,,,
,
,
,
是等腰三角形,
,,
,
,为的中点,
是等腰三角形,,
,
,
∽,
,
,
.
,
设直线的解析式为,
,
解得.
直线的解析式为.
,
解得,,
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式;相似三角形的判定与性质;二次函数-动态几何问题;数学思想
16.【答案】(1)16
(2)
【知识点】两条直线被一组平行线所截,所得的对应线段成比例;相似三角形的判定与性质
17.【答案】(1);
(2)解:如图1,延长至点,使,连接.
图1
由(1)可知,,
,,,.
,,,
,.
,
,
,
,
为直角三角形.
(3)解:如图2,延长至点,使,连接,
图2
.
又,
,
.
,,
.
在中,由三角形三边关系可得,
即,
.
【知识点】三角形三边关系;勾股定理的逆定理;相似三角形的判定与性质;三角形全等的判定-SAS
18.【答案】(1)解:∵四边形是正方形,
∴.
由折叠的性质可知,,,
∴,
又∵,
∴.
由操作一知,
∴是等腰直角三角形,
∴N,
∴,
∴.
∵,
∴.
(2)解:成立,理由如下:
由折叠的性质可知,.
∵是等腰直角三角形,
∴,
∴.
∵,
∴,
∴.
∵,
∴,
∴.
(3)解:将三角形沿翻折,使点F落在点G处,连接交与点O,
∴,.
由折叠的性质得,
∴,
∴是等腰直角三角形,
∴,
∴.
∵四边形是矩形,
∴,,
∴,
∴.
设,则,
∴,.
在中,,
∵,
∴,
整理得,
∴或(舍去),
即.
【知识点】勾股定理;矩形的性质;正方形的性质;翻折变换(折叠问题);三角形全等的判定-ASA
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
