福建省龙岩市漳平第二中学2023-2024学年高一下学期第二次月考数学试题(含解析)
文档属性
| 名称 | 福建省龙岩市漳平第二中学2023-2024学年高一下学期第二次月考数学试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 15:06:02 | ||
图片预览




文档简介
漳平二中2023-2024学年下学期第二次月考
高一数学试卷
一、单选题
1.若,则的虚部为( )
A. B. C. D.
2.在△ABC中,角A,B,C所对的边分别为a,b,c,如果a=2,A=45°,B=30°,那么b=( )
A. B. C. D.
3.已知直线平面,直线平面,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知在正四面体中,M为AB的中点,则直线CM与AD所成角的余弦值为( )
A. B. C. D.
5.掷一枚均匀的正六面体骰子,设表示事件“出现2点”,表示“出现奇数点”,则等于( )
A. B. C. D.
6.已知圆锥的轴截面为正三角形,该圆锥的侧面积数值与其体积数值相等,则该圆锥的底面积为( )
A. B. C. D.
7.某校举办了数学知识竞赛,并将1000名学生的竞赛成绩(满分100分,成绩取整数)整理成如图所示的频率分布直方图,则以下四个说法正确的个数为( )
①a的值为0.005
②估计这组数据的众数为75
③估计这组数据的下四分位数为60
④估计成绩高于80分的有300人
A.1 B.2 C.3 D.4
8.如图,在棱长为a的正方体中,P在线段上,且,M为线段上的动点,则三棱锥的体积为( )
B.
C. D.与点M的位置有关
二、多选题
9.若复数z满足(i是虚数单位),则下列说法正确的是( )
A.z的虚部为 B.z的共轭复数为
C.z的模为 D.z在复平面内对应的点位于第四象限
10.有下列说法,其中错误的说法为( ).
A.、为实数,若,则与共线
B.若、,则
C.两个非零向量、,若,则与垂直
D.若,、分别表示、的面积,则
11.在如图所示的三棱锥中,,,,两两互相垂直,下列结论正确的为( )
A.直线与平面所成的角为
B.二面角的正切值为
C.到面的距离为
D.作平面,垂足为,则为的重心
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
12.如图,直角梯形ABCD是某个多边形的斜二测直观图,,,,则该多边形原本的面积为 .
13.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和为6的概率是 .
14.锐角中,内角A,B,C所对的边分别为a,b,c,且,若,则面积S的取值范围 .
四、解答题
15.已知向量,.
(1)若,求实数k的值;
(2)若,求实数k的值.
16.如图,在四棱锥中,底面是正方形,平面,且,点为线段的中点.
(1)求证:平面;
(2)求证:平面;
(3)求三棱锥的体积.
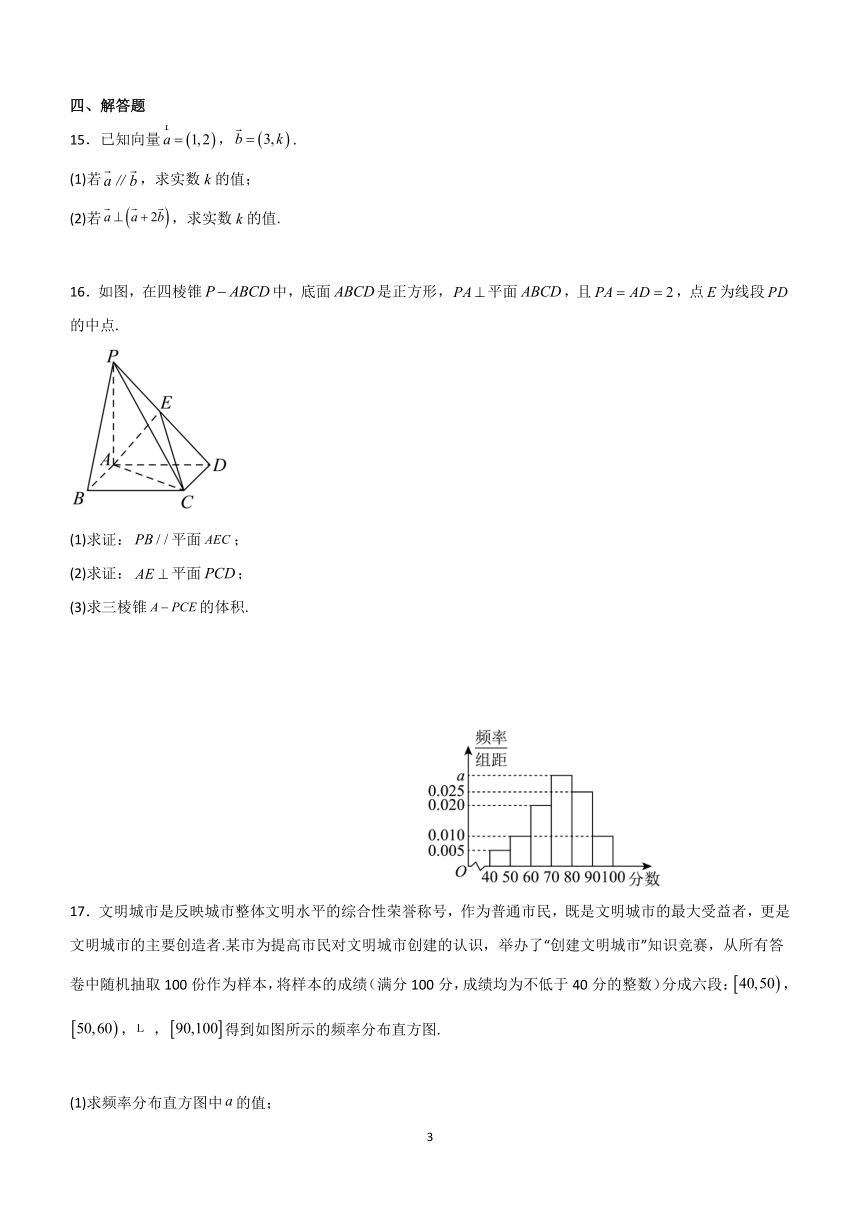
17.文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创造者.某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取100份作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:,,,得到如图所示的频率分布直方图.
(1)求频率分布直方图中的值;
(2)求样本成绩的第75百分位数;
(3)已知落在的平均成绩是61,方差是7,落在的平均成绩为70,方差是4,求两组成绩的总平均数和总方差.
18.的内角的对边分别为,已知.
(1)求;
(2)若为锐角三角形,且,求面积的取值范围.
19.如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EF∥AB,现将四边形ABCD沿EF折起,使BE⊥EC.
(1)若BE=1,在折叠后的线段AD上是否存在一点P,使得CP∥平面ABEF?若存在,求出的值;若不存在,说明理由.
(2)求三棱锥A CDF的体积的最大值,并求出此时点F到平面ACD的距离.
参考答案
1.D【详解】由得,故的虚部为,故选:D.
2.A【详解】因为在△ABC中,a=2,A=45°,B=30°,所以由正弦定理得,
解得,故选:A.
【点睛】本题在考查正弦定理的应用,属于基础题》
3.A【详解】因为直线平面,直线平面,当时,可得,即充分性满足;当时,不一定平行,有可能相交还有可能异面,故必要性不满足;所以“”是“”的充分不必要条件.故选:A
4.C【详解】设正四面体的棱长为2,取BD的中点N,连接MN,CN,如图, 由M是AB的中点,得,则是CM与AD所成的角或其补角,显然,取MN的中点E,连接CE,则,
在中,,因此,
所以直线CM与AD所成角的余弦值为.故选:C
B【详解】掷一枚均匀的正六面体骰子,共有六个基本事件,因为A表示事件“出现2点”,B表示“出现奇数点”,所以表示事件为出现2点、1点、3点、5点这四个基本事件,因此故选:B
6.B【详解】几何体如图所示:因为轴截面是正三角形,所以.圆锥的侧面积等于,
圆锥的体积等于,由圆锥的侧面积数值与其体积数值相等,得,得.
故圆锥的底面积为.故选:B.
7.D【详解】由频率分布直方图可知,解得,①正确;
根据频率分布直方图可知众数落在区间,用区间中点表示众数,即众数为75,②正确;前两组频率之和为,所以这组数据的下四分位数为60,③正确;成绩高于80分的频率,所以估计总体成绩高于80分的有人,④正确;综上①②③④正确,故选:D
8.A【详解】由题意知,点到平面MBC的距离为a,又,所以点到平面MBC的距离为,
又点M在上运动,所以,所以,故选:A.
9.ACD【详解】由,得,则的虚部为,故A正确;
的共轭复数为,故B错误;的模为,故C正确;
在复平面内对应的点为,位于第四象限,故D正确.故选:ACD.
10.AB【详解】解:对于A选项,当时,与可以为任意向量,满足,但与不一定共线,故A错误,对于B选项,如果、都是非零向量,,满足已知条件,但是结论不成立,故B错,
对于C选项,若,所以,即,即,所以,∴与垂直,故C正确,
若,设,,可得为的重心,
设,,,则,,,由,
可得,故D正确;故选:AB.
11.BD解:因为,,两两互相垂直,,平面,故为直线与平面所成的角,又,所以,故直线与平面所成的角为,故A错误;
取中点为,连接,因为,,,两两互相垂直,所以,因为,所以平面,故为二面角的平面角,
则,故二面角的正切值为,故B项正确;因为,所以,设到面的距离为,则,解得,故C项错误;因为,故为等边三角形,因为平面,
则点为点在平面上的投影,又,
即点到顶点的距离相等,即点到顶点的距离相等,
故为的重心,故D项正确.故选:BD.
12.【详解】过点A作,垂足为E,易知为正方形,因为,,
所以,,所以,所以,根据斜二测画法还原后的平面图形,是上底为1,下底为2,高为的梯形,所以该多边形原本的面积为.故答案为:
13.【详解】将一颗质地均匀的骰子(一种各个面分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,基本事件总数,出现向上的点数之和等于6包含的基本事件有:,共5个,
∴出现向上的点数之和等于6的概率为.故答案为:.
14.【详解】因为,所以由正弦定理有,整理得,
所以由余弦定理有,又,所以,又,所以由正弦定理有,因为为锐角三角形,所以且,所以,所以,则,所以,即,
所以.故答案为:.
15.(1)(2)【详解】(1)由知,即.
(2)由,,知.由知,故,即,从而.
16.【详解】(1)连接交于点,连接,由底面是正方形,故为中点,又点为线段的中点,故,又平面,平面,故平面;
(2)由点为线段的中点,,故,
由平面,平面,故,又底面是正方形,故,
又、平面,,故平面,又平面,
故,又、平面,,故平面;
(3)由点为线段的中点,故点与点到平面距离相等,故.
17.【详解】(1)由每组小矩形的面积之和为1得,,所以.(2)成绩落在内的频率为,落在内的频率为,显然第75百分位数,由,解得,所以第75百分位数为84.
(3)由频率分布直方图知,成绩在的市民人数为,成绩在的市民人数为,所以;由样本方差计算总体方差公式,得总方差为.
18.【详解】(1)[方法一]【最优解:利用三角形内角和为结合正弦定理求角度】由三角形的内角和定理得,此时就变为.由诱导公式得,所以.在中,由正弦定理知,此时就有,即,再由二倍角的正弦公式得,解得.
[方法二]【利用正弦定理解方程求得的值可得的值】
由解法1得,两边平方得,即.又,即,所以,进一步整理得,
解得,因此.
[方法三]【利用正弦定理结合三角形内角和为求得的比例关系】
根据题意,由正弦定理得,因为,故,
消去得.,,因为故或者,
而根据题意,故不成立,所以,又因为,代入得,所以.
(2)[方法一]【最优解:利用锐角三角形求得C的范围,然后由面积函数求面积的取值范围】
因为是锐角三角形,又,所以,
则.
因为,所以,则,从而,故面积的取值范围是.
[方法二]【由题意求得边的取值范围,然后结合面积公式求面积的取值范围】
由题设及(1)知的面积.因为为锐角三角形,且,所以即又由余弦定理得,所以即,所以,故面积的取值范围是.
[方法三]【数形结合,利用极限的思想求解三角形面积的取值范围】
如图,在中,过点A作,垂足为,作与交于点.
由题设及(1)知的面积,因为为锐角三角形,且,
所以点C位于在线段上且不含端点,从而,
即,即,所以,故面积的取值范围是.
19.【详解】(1)AD上存在一点P,使得CP∥平面ABEF,此时.理由如下:当时,,
如图,过点P作MP∥FD交AF于点M,连接ME,则,∵BE=1,∴FD=5,∴MP=3,又EC=3,MP∥FD∥EC,∴MP∥EC,故四边形MPCE为平行四边形,∴CP∥ME,又CP 平面ABEF,ME 平面ABEF,
∴CP∥平面ABEF.
(2)设BE=x,则AF=x(0∴当x=3时,VA-CDF有最大值,且最大值为3,此时EC=1,AF=3,FD=3,.
∴,.在△ACD中,由余弦定理得
,,.设到平面的距离为,
,.
高一数学试卷
一、单选题
1.若,则的虚部为( )
A. B. C. D.
2.在△ABC中,角A,B,C所对的边分别为a,b,c,如果a=2,A=45°,B=30°,那么b=( )
A. B. C. D.
3.已知直线平面,直线平面,则“”是“”的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
4.已知在正四面体中,M为AB的中点,则直线CM与AD所成角的余弦值为( )
A. B. C. D.
5.掷一枚均匀的正六面体骰子,设表示事件“出现2点”,表示“出现奇数点”,则等于( )
A. B. C. D.
6.已知圆锥的轴截面为正三角形,该圆锥的侧面积数值与其体积数值相等,则该圆锥的底面积为( )
A. B. C. D.
7.某校举办了数学知识竞赛,并将1000名学生的竞赛成绩(满分100分,成绩取整数)整理成如图所示的频率分布直方图,则以下四个说法正确的个数为( )
①a的值为0.005
②估计这组数据的众数为75
③估计这组数据的下四分位数为60
④估计成绩高于80分的有300人
A.1 B.2 C.3 D.4
8.如图,在棱长为a的正方体中,P在线段上,且,M为线段上的动点,则三棱锥的体积为( )
B.
C. D.与点M的位置有关
二、多选题
9.若复数z满足(i是虚数单位),则下列说法正确的是( )
A.z的虚部为 B.z的共轭复数为
C.z的模为 D.z在复平面内对应的点位于第四象限
10.有下列说法,其中错误的说法为( ).
A.、为实数,若,则与共线
B.若、,则
C.两个非零向量、,若,则与垂直
D.若,、分别表示、的面积,则
11.在如图所示的三棱锥中,,,,两两互相垂直,下列结论正确的为( )
A.直线与平面所成的角为
B.二面角的正切值为
C.到面的距离为
D.作平面,垂足为,则为的重心
第II卷(非选择题)
请点击修改第II卷的文字说明
三、填空题
12.如图,直角梯形ABCD是某个多边形的斜二测直观图,,,,则该多边形原本的面积为 .
13.将一颗质地均匀的骰子(一种各个面上分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,则出现向上的点数之和为6的概率是 .
14.锐角中,内角A,B,C所对的边分别为a,b,c,且,若,则面积S的取值范围 .
四、解答题
15.已知向量,.
(1)若,求实数k的值;
(2)若,求实数k的值.
16.如图,在四棱锥中,底面是正方形,平面,且,点为线段的中点.
(1)求证:平面;
(2)求证:平面;
(3)求三棱锥的体积.
17.文明城市是反映城市整体文明水平的综合性荣誉称号,作为普通市民,既是文明城市的最大受益者,更是文明城市的主要创造者.某市为提高市民对文明城市创建的认识,举办了“创建文明城市”知识竞赛,从所有答卷中随机抽取100份作为样本,将样本的成绩(满分100分,成绩均为不低于40分的整数)分成六段:,,,得到如图所示的频率分布直方图.
(1)求频率分布直方图中的值;
(2)求样本成绩的第75百分位数;
(3)已知落在的平均成绩是61,方差是7,落在的平均成绩为70,方差是4,求两组成绩的总平均数和总方差.
18.的内角的对边分别为,已知.
(1)求;
(2)若为锐角三角形,且,求面积的取值范围.
19.如图,四边形ABCD中,AB⊥AD,AD∥BC,AD=6,BC=2AB=4,E,F分别在BC,AD上,EF∥AB,现将四边形ABCD沿EF折起,使BE⊥EC.
(1)若BE=1,在折叠后的线段AD上是否存在一点P,使得CP∥平面ABEF?若存在,求出的值;若不存在,说明理由.
(2)求三棱锥A CDF的体积的最大值,并求出此时点F到平面ACD的距离.
参考答案
1.D【详解】由得,故的虚部为,故选:D.
2.A【详解】因为在△ABC中,a=2,A=45°,B=30°,所以由正弦定理得,
解得,故选:A.
【点睛】本题在考查正弦定理的应用,属于基础题》
3.A【详解】因为直线平面,直线平面,当时,可得,即充分性满足;当时,不一定平行,有可能相交还有可能异面,故必要性不满足;所以“”是“”的充分不必要条件.故选:A
4.C【详解】设正四面体的棱长为2,取BD的中点N,连接MN,CN,如图, 由M是AB的中点,得,则是CM与AD所成的角或其补角,显然,取MN的中点E,连接CE,则,
在中,,因此,
所以直线CM与AD所成角的余弦值为.故选:C
B【详解】掷一枚均匀的正六面体骰子,共有六个基本事件,因为A表示事件“出现2点”,B表示“出现奇数点”,所以表示事件为出现2点、1点、3点、5点这四个基本事件,因此故选:B
6.B【详解】几何体如图所示:因为轴截面是正三角形,所以.圆锥的侧面积等于,
圆锥的体积等于,由圆锥的侧面积数值与其体积数值相等,得,得.
故圆锥的底面积为.故选:B.
7.D【详解】由频率分布直方图可知,解得,①正确;
根据频率分布直方图可知众数落在区间,用区间中点表示众数,即众数为75,②正确;前两组频率之和为,所以这组数据的下四分位数为60,③正确;成绩高于80分的频率,所以估计总体成绩高于80分的有人,④正确;综上①②③④正确,故选:D
8.A【详解】由题意知,点到平面MBC的距离为a,又,所以点到平面MBC的距离为,
又点M在上运动,所以,所以,故选:A.
9.ACD【详解】由,得,则的虚部为,故A正确;
的共轭复数为,故B错误;的模为,故C正确;
在复平面内对应的点为,位于第四象限,故D正确.故选:ACD.
10.AB【详解】解:对于A选项,当时,与可以为任意向量,满足,但与不一定共线,故A错误,对于B选项,如果、都是非零向量,,满足已知条件,但是结论不成立,故B错,
对于C选项,若,所以,即,即,所以,∴与垂直,故C正确,
若,设,,可得为的重心,
设,,,则,,,由,
可得,故D正确;故选:AB.
11.BD解:因为,,两两互相垂直,,平面,故为直线与平面所成的角,又,所以,故直线与平面所成的角为,故A错误;
取中点为,连接,因为,,,两两互相垂直,所以,因为,所以平面,故为二面角的平面角,
则,故二面角的正切值为,故B项正确;因为,所以,设到面的距离为,则,解得,故C项错误;因为,故为等边三角形,因为平面,
则点为点在平面上的投影,又,
即点到顶点的距离相等,即点到顶点的距离相等,
故为的重心,故D项正确.故选:BD.
12.【详解】过点A作,垂足为E,易知为正方形,因为,,
所以,,所以,所以,根据斜二测画法还原后的平面图形,是上底为1,下底为2,高为的梯形,所以该多边形原本的面积为.故答案为:
13.【详解】将一颗质地均匀的骰子(一种各个面分别标有1,2,3,4,5,6个点的正方体玩具)先后抛掷2次,基本事件总数,出现向上的点数之和等于6包含的基本事件有:,共5个,
∴出现向上的点数之和等于6的概率为.故答案为:.
14.【详解】因为,所以由正弦定理有,整理得,
所以由余弦定理有,又,所以,又,所以由正弦定理有,因为为锐角三角形,所以且,所以,所以,则,所以,即,
所以.故答案为:.
15.(1)(2)【详解】(1)由知,即.
(2)由,,知.由知,故,即,从而.
16.【详解】(1)连接交于点,连接,由底面是正方形,故为中点,又点为线段的中点,故,又平面,平面,故平面;
(2)由点为线段的中点,,故,
由平面,平面,故,又底面是正方形,故,
又、平面,,故平面,又平面,
故,又、平面,,故平面;
(3)由点为线段的中点,故点与点到平面距离相等,故.
17.【详解】(1)由每组小矩形的面积之和为1得,,所以.(2)成绩落在内的频率为,落在内的频率为,显然第75百分位数,由,解得,所以第75百分位数为84.
(3)由频率分布直方图知,成绩在的市民人数为,成绩在的市民人数为,所以;由样本方差计算总体方差公式,得总方差为.
18.【详解】(1)[方法一]【最优解:利用三角形内角和为结合正弦定理求角度】由三角形的内角和定理得,此时就变为.由诱导公式得,所以.在中,由正弦定理知,此时就有,即,再由二倍角的正弦公式得,解得.
[方法二]【利用正弦定理解方程求得的值可得的值】
由解法1得,两边平方得,即.又,即,所以,进一步整理得,
解得,因此.
[方法三]【利用正弦定理结合三角形内角和为求得的比例关系】
根据题意,由正弦定理得,因为,故,
消去得.,,因为故或者,
而根据题意,故不成立,所以,又因为,代入得,所以.
(2)[方法一]【最优解:利用锐角三角形求得C的范围,然后由面积函数求面积的取值范围】
因为是锐角三角形,又,所以,
则.
因为,所以,则,从而,故面积的取值范围是.
[方法二]【由题意求得边的取值范围,然后结合面积公式求面积的取值范围】
由题设及(1)知的面积.因为为锐角三角形,且,所以即又由余弦定理得,所以即,所以,故面积的取值范围是.
[方法三]【数形结合,利用极限的思想求解三角形面积的取值范围】
如图,在中,过点A作,垂足为,作与交于点.
由题设及(1)知的面积,因为为锐角三角形,且,
所以点C位于在线段上且不含端点,从而,
即,即,所以,故面积的取值范围是.
19.【详解】(1)AD上存在一点P,使得CP∥平面ABEF,此时.理由如下:当时,,
如图,过点P作MP∥FD交AF于点M,连接ME,则,∵BE=1,∴FD=5,∴MP=3,又EC=3,MP∥FD∥EC,∴MP∥EC,故四边形MPCE为平行四边形,∴CP∥ME,又CP 平面ABEF,ME 平面ABEF,
∴CP∥平面ABEF.
(2)设BE=x,则AF=x(0
∴,.在△ACD中,由余弦定理得
,,.设到平面的距离为,
,.
同课章节目录
