八、数据的表示和分析——复式折线统计图(同步练习)(含答案)北师大版五年级数学下册
文档属性
| 名称 | 八、数据的表示和分析——复式折线统计图(同步练习)(含答案)北师大版五年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 586.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-12 15:24:46 | ||
图片预览


文档简介
八、数据的表示和分析——复式折线统计图(同步练习)
(含答案)北师大版五年级数学下册
一、填空题
1.要统计甲、乙两个城市2024年1~5月的月平均气温的变化情况应绘制( )统计图。
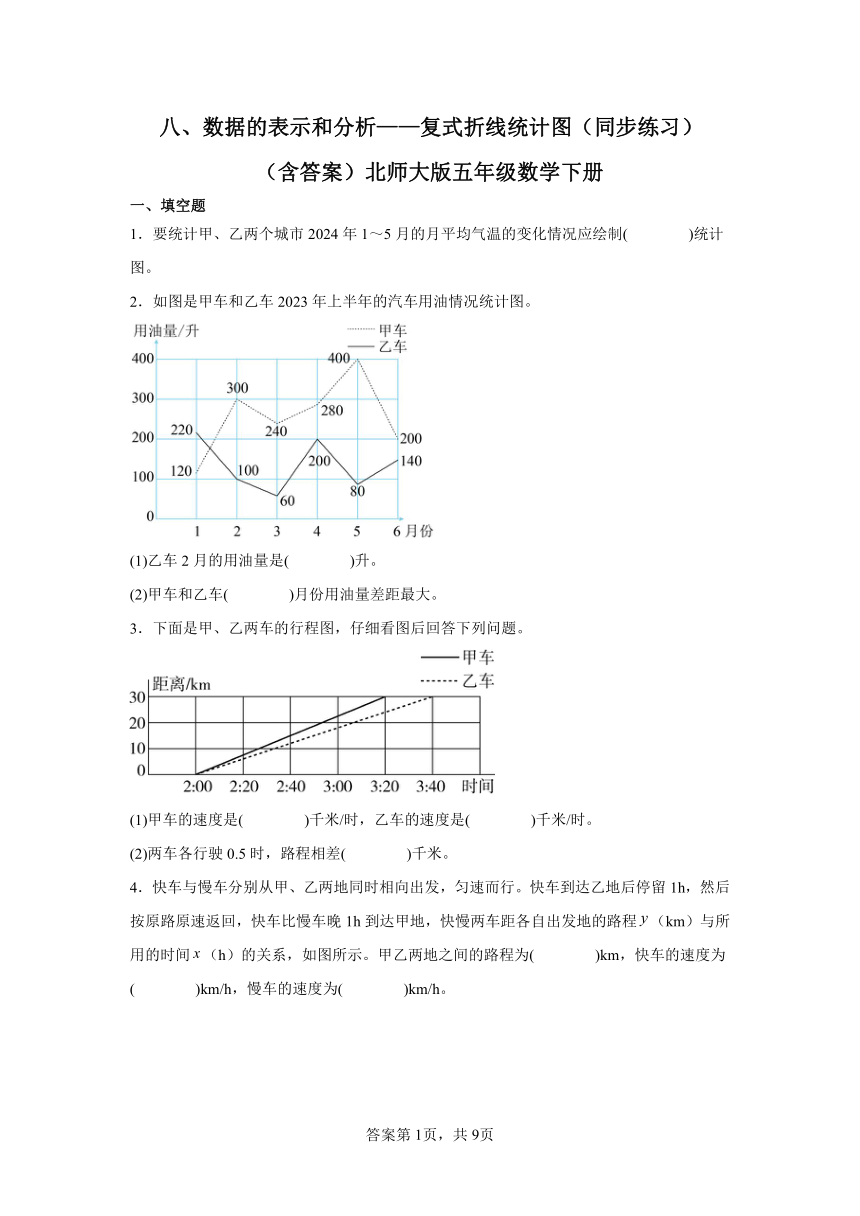
2.如图是甲车和乙车2023年上半年的汽车用油情况统计图。
(1)乙车2月的用油量是( )升。
(2)甲车和乙车( )月份用油量差距最大。
3.下面是甲、乙两车的行程图,仔细看图后回答下列问题。
(1)甲车的速度是( )千米/时,乙车的速度是( )千米/时。
(2)两车各行驶0.5时,路程相差( )千米。
4.快车与慢车分别从甲、乙两地同时相向出发,匀速而行。快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程(km)与所用的时间(h)的关系,如图所示。甲乙两地之间的路程为( )km,快车的速度为( )km/h,慢车的速度为( )km/h。
5.下面是奇思和妙想在学校运动会中100米赛跑的情况统计图。
奇思和妙想100米赛跑情况统计图
(1)从图中可以看出,( )用时较多,比另一人多用时( )秒。
(2)妙想到达终点时,奇思距离终点还有( )米。
(3)比赛开始时妙想比奇思慢一些,大约在第( )秒的时候妙想追上了奇思。
二、选择题
6.要清楚地表示甲、乙两个城市2021年上半年月平均气温变化情况,一般选用( )统计图。
A.折线 B.复式条形 C.条形 D.复式折线
7.六(1)班老师要统计本班期末考试语文、数学成绩中各分数段的人数,应制作( )。
A.单式条形统计图 B.复式条形统计图
C.单式折线统计图 D.复式折线统计图
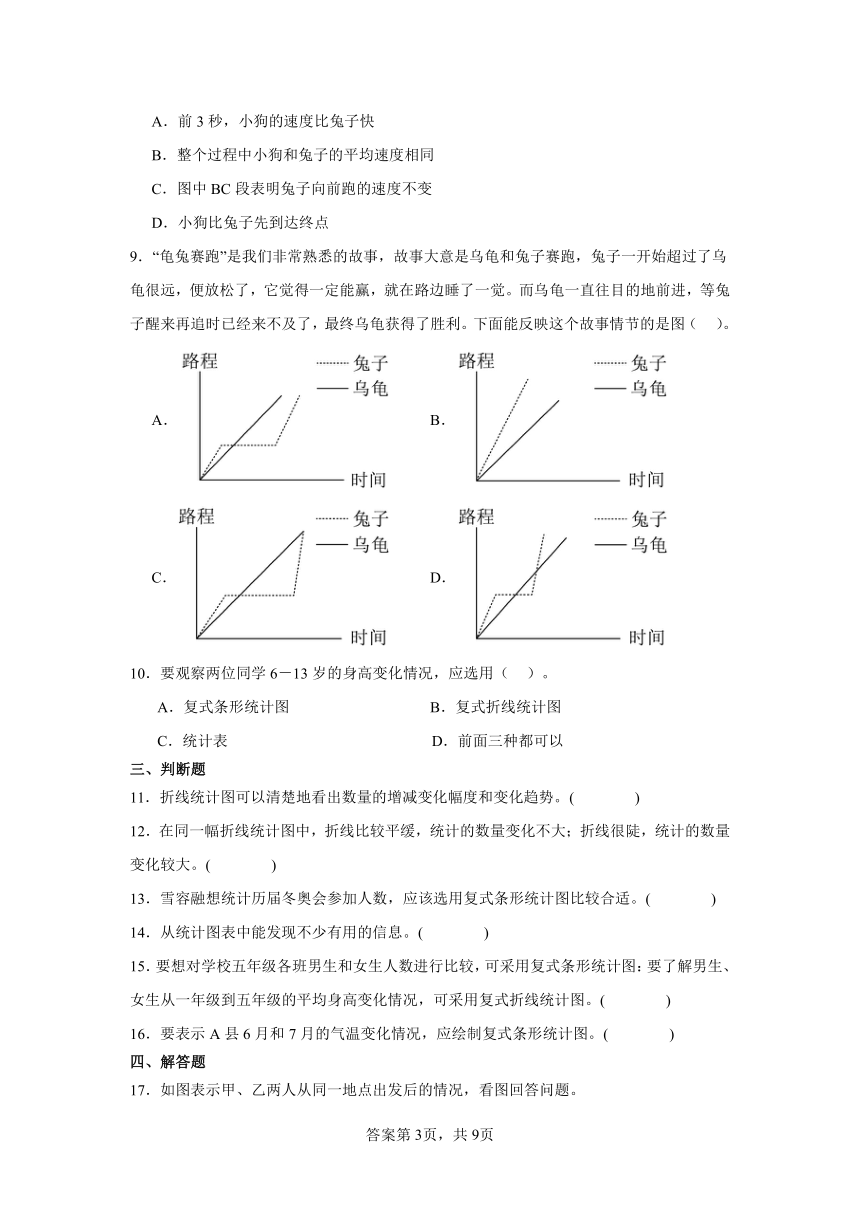
8.森林运动会开始了,一只兔子和一条小狗赛跑,兔子跑的路程与时间关系图象如图中实线部分ABCD所示,小狗跑的路程与时间关系图象如图中虚线部分AD所示。则关于该图象下列说法正确的是( )。
A.前3秒,小狗的速度比兔子快
B.整个过程中小狗和兔子的平均速度相同
C.图中BC段表明兔子向前跑的速度不变
D.小狗比兔子先到达终点
9.“龟兔赛跑”是我们非常熟悉的故事,故事大意是乌龟和兔子赛跑,兔子一开始超过了乌龟很远,便放松了,它觉得一定能赢,就在路边睡了一觉。而乌龟一直往目的地前进,等兔子醒来再追时已经来不及了,最终乌龟获得了胜利。下面能反映这个故事情节的是图( )。
A. B.
C. D.
10.要观察两位同学6-13岁的身高变化情况,应选用( )。
A.复式条形统计图 B.复式折线统计图
C.统计表 D.前面三种都可以
三、判断题
11.折线统计图可以清楚地看出数量的增减变化幅度和变化趋势。( )
12.在同一幅折线统计图中,折线比较平缓,统计的数量变化不大;折线很陡,统计的数量变化较大。( )
13.雪容融想统计历届冬奥会参加人数,应该选用复式条形统计图比较合适。( )
14.从统计图表中能发现不少有用的信息。( )
15.要想对学校五年级各班男生和女生人数进行比较,可采用复式条形统计图:要了解男生、女生从一年级到五年级的平均身高变化情况,可采用复式折线统计图。( )
16.要表示A县6月和7月的气温变化情况,应绘制复式条形统计图。( )
四、解答题
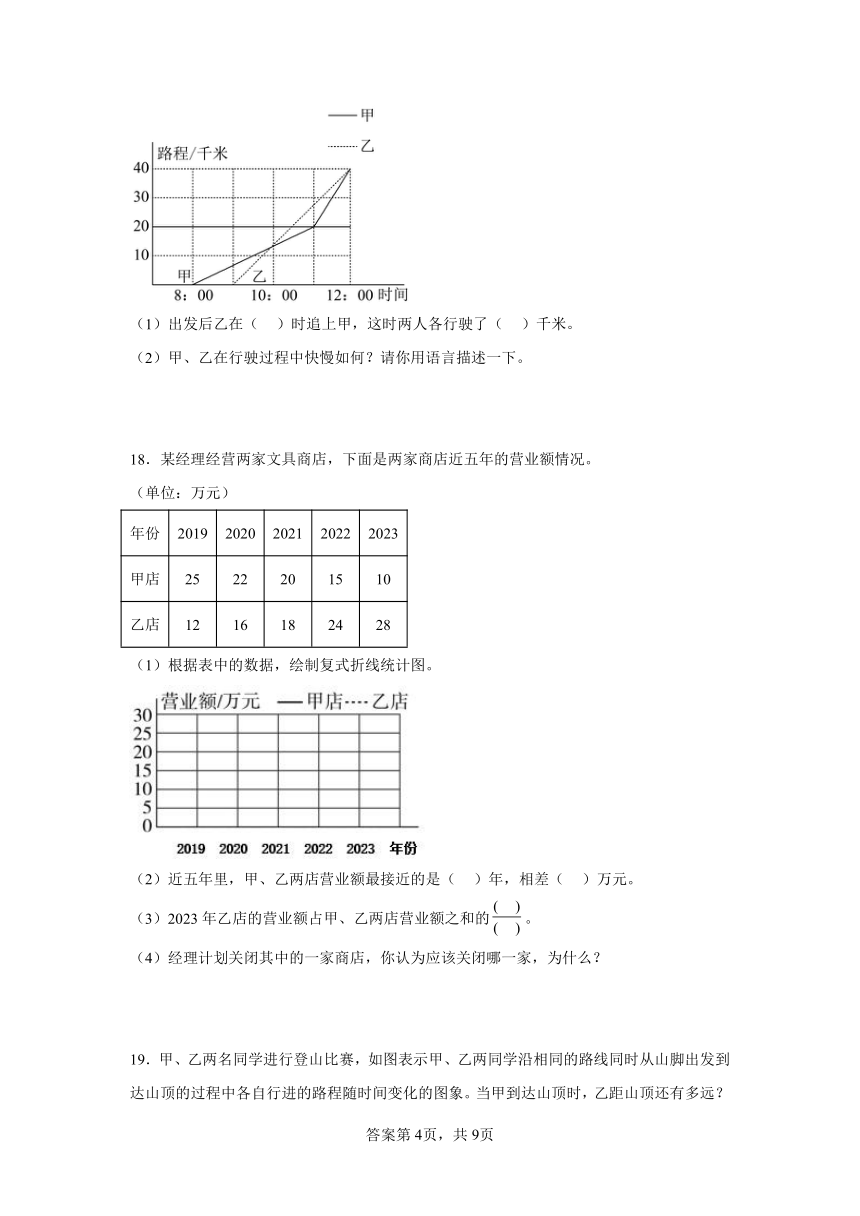
17.如图表示甲、乙两人从同一地点出发后的情况,看图回答问题。
(1)出发后乙在( )时追上甲,这时两人各行驶了( )千米。
(2)甲、乙在行驶过程中快慢如何?请你用语言描述一下。
18.某经理经营两家文具商店,下面是两家商店近五年的营业额情况。
(单位:万元)
年份 2019 2020 2021 2022 2023
甲店 25 22 20 15 10
乙店 12 16 18 24 28
(1)根据表中的数据,绘制复式折线统计图。
(2)近五年里,甲、乙两店营业额最接近的是( )年,相差( )万元。
(3)2023年乙店的营业额占甲、乙两店营业额之和的。
(4)经理计划关闭其中的一家商店,你认为应该关闭哪一家,为什么?
19.甲、乙两名同学进行登山比赛,如图表示甲、乙两同学沿相同的路线同时从山脚出发到达山顶的过程中各自行进的路程随时间变化的图象。当甲到达山顶时,乙距山顶还有多远?
20.2023年,某软件公司发明了两个古诗文学习软件,供小学生自学。下面是某地六个年级使用软件A和软件B的人数数据统计表。请根据统计表完成下面的统计图。
年级 一 二 三 四 五 六
软件A 1600 2000 1900 1700 1300 1850
软件B 680 460 1000 1100 1550 960
(1)从图中可以看出,( )年级使用两种软件的人数相差最大。
(2)你认为哪种软件更受大家欢迎?
21.下面是某地区7~15岁男生、女生平均身高统计图。
这是一个复式( )统计图。
(1)这个统计图你看懂了吗?与同伴说一说。
(2)统计图中,男生和女生平均身高差别最大的是( )岁,相差( )厘米。
(3)8岁时,( )平均身高比较高,女生( )岁起平均身高增长速度明显减缓。
(4)从7岁到15岁,男生平均身高共增长了( )厘米,估计16岁时男生的平均身高为( )厘米。
参考答案:
1.复式折线 2.(1)100 (2)5
3.(1) 22.5 18 (2)2.25
4. 840 280 140
5.(1) 奇思 2 (2)13 (3)9
6.D
7.B
8.B
9.A
10.B
11.√
12.√
13.√
14.√
15.√
16.×
17.(1)乙的速度:
40÷(12-9)
=40÷3
=(千米/时)
×(10-9)
=×1
=(千米)
出发后乙在10时追上甲,这时两人各行驶了千米。
(2)甲8时到11时的速度:
20÷(11-8)
=20÷3
=(千米/时)
甲11时到12时的速度:
(40-20)÷(12-11)
=20÷1
=20(千米/时)
甲从8时到11时速度较慢,每时行千米;从11时到12时加快了速度,每时行20千米。乙的速度一直保持每时行千米。(答案不唯一)
18.(1)如图:
(2)(万元)
从统计图中可以看出,近五年里,甲、乙两店营业额最接近的是2021年,相差2万元。
(3)
2023年乙店的营业额占甲、乙两店营业额之和的。
(4)我认为应该关闭甲店;因为甲店的营业额近5年持续下降,到2023年已经远远低于乙店,而乙店的营业额近5年在持续上升。(合理即可,答案不唯一)
19.甲的速度:6÷2=3(千米/时)
乙的速度:6÷3=2(千米/时)
甲登山时间:12÷3=4(时)
乙登山时间:12÷2=6(时)
2×(6-4)
=2×2
=4(千米)
答:当甲到达山顶时,乙距山顶还有4千米。
20.如图:
(1)从图中可以看出,二年级使用两种软件的人数相差最大。
(2)因为各年级使用软件A的人数比使用软件B的人数多,所以我认为软件A更受大家欢迎。
21.这是一个复式折线统计图。
(1)这个统计图我看懂了。复式折线统计图的横轴表示年龄,纵轴表示身高;黄色的折线代表男生的平均身高,绿色的折线代表女生的平均身高;从两条折线的变化趋势中可以看出,7~15岁男生、女生平均身高都呈逐渐上升趋势,7~12岁女生的平均身高比男生的高,13~15岁男生的平均身高比女生的高。(答案不唯一)
(2)167-158=9(厘米)
统计图中,男生和女生平均身高差别最大的是15岁,相差9厘米。
(3)132>127
8岁时,女生平均身高比较高,女生13岁起平均身高增长速度明显减缓。
(4)167-123=44(厘米)
167+5=172(厘米)
从7岁到15岁,男生平均身高共增长了44厘米,估计16岁时男生的平均身高为172厘米。(第二个空答案不唯一)
答案第1页,共2页
答案第1页,共2页
(含答案)北师大版五年级数学下册
一、填空题
1.要统计甲、乙两个城市2024年1~5月的月平均气温的变化情况应绘制( )统计图。
2.如图是甲车和乙车2023年上半年的汽车用油情况统计图。
(1)乙车2月的用油量是( )升。
(2)甲车和乙车( )月份用油量差距最大。
3.下面是甲、乙两车的行程图,仔细看图后回答下列问题。
(1)甲车的速度是( )千米/时,乙车的速度是( )千米/时。
(2)两车各行驶0.5时,路程相差( )千米。
4.快车与慢车分别从甲、乙两地同时相向出发,匀速而行。快车到达乙地后停留1h,然后按原路原速返回,快车比慢车晚1h到达甲地,快慢两车距各自出发地的路程(km)与所用的时间(h)的关系,如图所示。甲乙两地之间的路程为( )km,快车的速度为( )km/h,慢车的速度为( )km/h。
5.下面是奇思和妙想在学校运动会中100米赛跑的情况统计图。
奇思和妙想100米赛跑情况统计图
(1)从图中可以看出,( )用时较多,比另一人多用时( )秒。
(2)妙想到达终点时,奇思距离终点还有( )米。
(3)比赛开始时妙想比奇思慢一些,大约在第( )秒的时候妙想追上了奇思。
二、选择题
6.要清楚地表示甲、乙两个城市2021年上半年月平均气温变化情况,一般选用( )统计图。
A.折线 B.复式条形 C.条形 D.复式折线
7.六(1)班老师要统计本班期末考试语文、数学成绩中各分数段的人数,应制作( )。
A.单式条形统计图 B.复式条形统计图
C.单式折线统计图 D.复式折线统计图
8.森林运动会开始了,一只兔子和一条小狗赛跑,兔子跑的路程与时间关系图象如图中实线部分ABCD所示,小狗跑的路程与时间关系图象如图中虚线部分AD所示。则关于该图象下列说法正确的是( )。
A.前3秒,小狗的速度比兔子快
B.整个过程中小狗和兔子的平均速度相同
C.图中BC段表明兔子向前跑的速度不变
D.小狗比兔子先到达终点
9.“龟兔赛跑”是我们非常熟悉的故事,故事大意是乌龟和兔子赛跑,兔子一开始超过了乌龟很远,便放松了,它觉得一定能赢,就在路边睡了一觉。而乌龟一直往目的地前进,等兔子醒来再追时已经来不及了,最终乌龟获得了胜利。下面能反映这个故事情节的是图( )。
A. B.
C. D.
10.要观察两位同学6-13岁的身高变化情况,应选用( )。
A.复式条形统计图 B.复式折线统计图
C.统计表 D.前面三种都可以
三、判断题
11.折线统计图可以清楚地看出数量的增减变化幅度和变化趋势。( )
12.在同一幅折线统计图中,折线比较平缓,统计的数量变化不大;折线很陡,统计的数量变化较大。( )
13.雪容融想统计历届冬奥会参加人数,应该选用复式条形统计图比较合适。( )
14.从统计图表中能发现不少有用的信息。( )
15.要想对学校五年级各班男生和女生人数进行比较,可采用复式条形统计图:要了解男生、女生从一年级到五年级的平均身高变化情况,可采用复式折线统计图。( )
16.要表示A县6月和7月的气温变化情况,应绘制复式条形统计图。( )
四、解答题
17.如图表示甲、乙两人从同一地点出发后的情况,看图回答问题。
(1)出发后乙在( )时追上甲,这时两人各行驶了( )千米。
(2)甲、乙在行驶过程中快慢如何?请你用语言描述一下。
18.某经理经营两家文具商店,下面是两家商店近五年的营业额情况。
(单位:万元)
年份 2019 2020 2021 2022 2023
甲店 25 22 20 15 10
乙店 12 16 18 24 28
(1)根据表中的数据,绘制复式折线统计图。
(2)近五年里,甲、乙两店营业额最接近的是( )年,相差( )万元。
(3)2023年乙店的营业额占甲、乙两店营业额之和的。
(4)经理计划关闭其中的一家商店,你认为应该关闭哪一家,为什么?
19.甲、乙两名同学进行登山比赛,如图表示甲、乙两同学沿相同的路线同时从山脚出发到达山顶的过程中各自行进的路程随时间变化的图象。当甲到达山顶时,乙距山顶还有多远?
20.2023年,某软件公司发明了两个古诗文学习软件,供小学生自学。下面是某地六个年级使用软件A和软件B的人数数据统计表。请根据统计表完成下面的统计图。
年级 一 二 三 四 五 六
软件A 1600 2000 1900 1700 1300 1850
软件B 680 460 1000 1100 1550 960
(1)从图中可以看出,( )年级使用两种软件的人数相差最大。
(2)你认为哪种软件更受大家欢迎?
21.下面是某地区7~15岁男生、女生平均身高统计图。
这是一个复式( )统计图。
(1)这个统计图你看懂了吗?与同伴说一说。
(2)统计图中,男生和女生平均身高差别最大的是( )岁,相差( )厘米。
(3)8岁时,( )平均身高比较高,女生( )岁起平均身高增长速度明显减缓。
(4)从7岁到15岁,男生平均身高共增长了( )厘米,估计16岁时男生的平均身高为( )厘米。
参考答案:
1.复式折线 2.(1)100 (2)5
3.(1) 22.5 18 (2)2.25
4. 840 280 140
5.(1) 奇思 2 (2)13 (3)9
6.D
7.B
8.B
9.A
10.B
11.√
12.√
13.√
14.√
15.√
16.×
17.(1)乙的速度:
40÷(12-9)
=40÷3
=(千米/时)
×(10-9)
=×1
=(千米)
出发后乙在10时追上甲,这时两人各行驶了千米。
(2)甲8时到11时的速度:
20÷(11-8)
=20÷3
=(千米/时)
甲11时到12时的速度:
(40-20)÷(12-11)
=20÷1
=20(千米/时)
甲从8时到11时速度较慢,每时行千米;从11时到12时加快了速度,每时行20千米。乙的速度一直保持每时行千米。(答案不唯一)
18.(1)如图:
(2)(万元)
从统计图中可以看出,近五年里,甲、乙两店营业额最接近的是2021年,相差2万元。
(3)
2023年乙店的营业额占甲、乙两店营业额之和的。
(4)我认为应该关闭甲店;因为甲店的营业额近5年持续下降,到2023年已经远远低于乙店,而乙店的营业额近5年在持续上升。(合理即可,答案不唯一)
19.甲的速度:6÷2=3(千米/时)
乙的速度:6÷3=2(千米/时)
甲登山时间:12÷3=4(时)
乙登山时间:12÷2=6(时)
2×(6-4)
=2×2
=4(千米)
答:当甲到达山顶时,乙距山顶还有4千米。
20.如图:
(1)从图中可以看出,二年级使用两种软件的人数相差最大。
(2)因为各年级使用软件A的人数比使用软件B的人数多,所以我认为软件A更受大家欢迎。
21.这是一个复式折线统计图。
(1)这个统计图我看懂了。复式折线统计图的横轴表示年龄,纵轴表示身高;黄色的折线代表男生的平均身高,绿色的折线代表女生的平均身高;从两条折线的变化趋势中可以看出,7~15岁男生、女生平均身高都呈逐渐上升趋势,7~12岁女生的平均身高比男生的高,13~15岁男生的平均身高比女生的高。(答案不唯一)
(2)167-158=9(厘米)
统计图中,男生和女生平均身高差别最大的是15岁,相差9厘米。
(3)132>127
8岁时,女生平均身高比较高,女生13岁起平均身高增长速度明显减缓。
(4)167-123=44(厘米)
167+5=172(厘米)
从7岁到15岁,男生平均身高共增长了44厘米,估计16岁时男生的平均身高为172厘米。(第二个空答案不唯一)
答案第1页,共2页
答案第1页,共2页
