沪科版八年级数学上册试题 第12章 一次函数 章节测试卷 (含解析)
文档属性
| 名称 | 沪科版八年级数学上册试题 第12章 一次函数 章节测试卷 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 470.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 08:12:22 | ||
图片预览



文档简介
第12章《一次函数》章节测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.在平面直角坐标系中,已知直线与直线平行,且与轴交于点,与轴的交点为,则的面积为( )
A.2022 B.1011 C.8 D.4
2.当时,对于x的每一个值,函数(k≠0)的值都小于函数的值,则k的取值范围是( )
A.且 B. C. D.
3.已知,,为直线上的三个点,且,则以下判断正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.关于函数(为常数),有下列结论:①当时,此函数是一次函数;②无论取什么值,函数图像必经过点;③若图像经过二、三、四象限,则的取值范围是;④若函数图像与轴的交点始终在正半轴,则的取值范围是.其中,正确结论的个数是( ).
A.1 B.2 C.3 D.4
5.若平面直角坐标系内的点满足横,纵坐标都为整数,则把点叫做“整点”,例如,,都是“整点”,四边形(为原点)为正方形且点坐标为,有4条直线,其中,,,互不相等,则这4条直线在正方形内(包括边上)经过的整点个数最多是( )个.
A.22 B.24 C.28 D.25
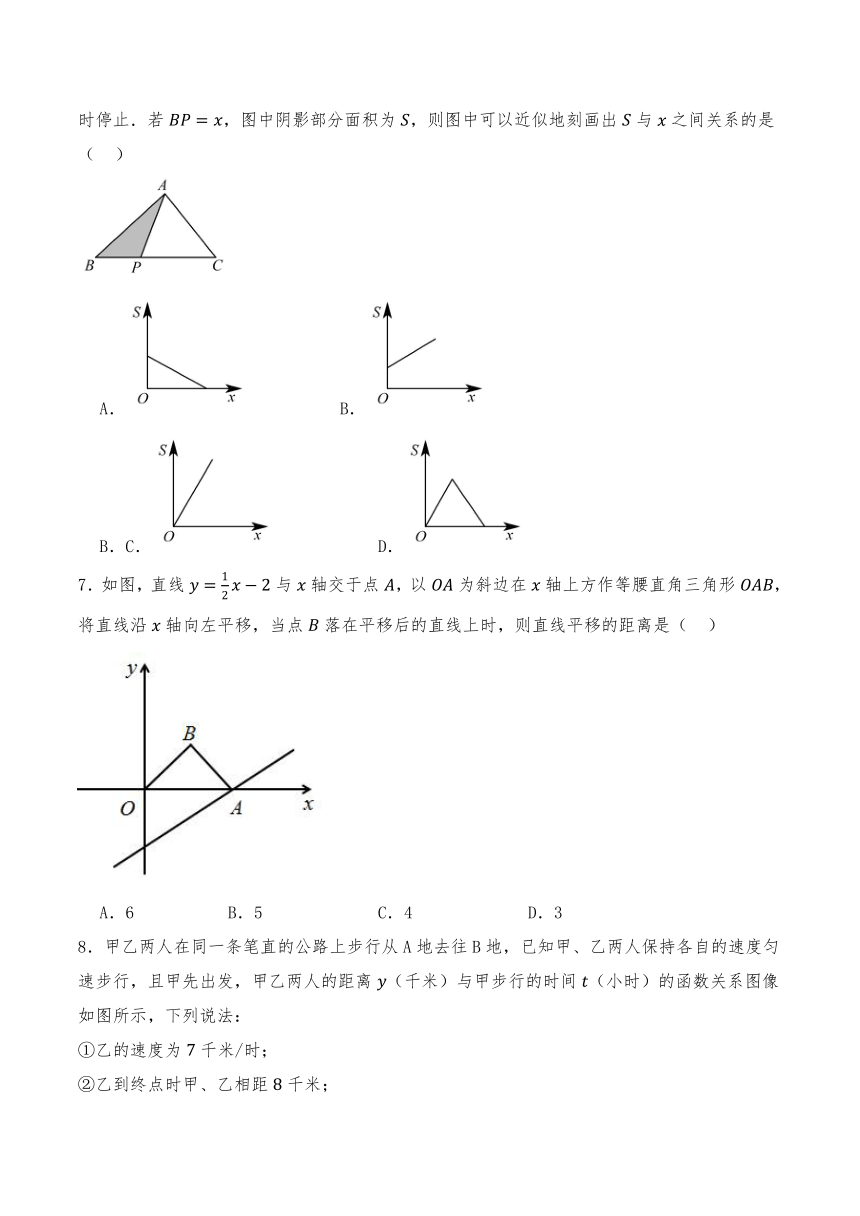
6.如图,在中,点是边上一点,点从点出发沿向点运动,到达点时停止.若,图中阴影部分面积为,则图中可以近似地刻画出与之间关系的是( )
B.
C. D.
7.如图,直线与轴交于点,以为斜边在轴上方作等腰直角三角形,将直线沿轴向左平移,当点落在平移后的直线上时,则直线平移的距离是( )
A.6 B.5 C.4 D.3
8.甲乙两人在同一条笔直的公路上步行从A地去往B地,已知甲、乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离(千米)与甲步行的时间(小时)的函数关系图像如图所示,下列说法:
①乙的速度为千米/时;
②乙到终点时甲、乙相距千米;
③当乙追上甲时,两人距地千米;
④两地距离为千米.
其中错误的个数为( )
A.1个 B.2个 C.3个 D.4个
9.如图,分别是直线上的动点,若时,都有,则的取值范围为( )
A. B. C. D.
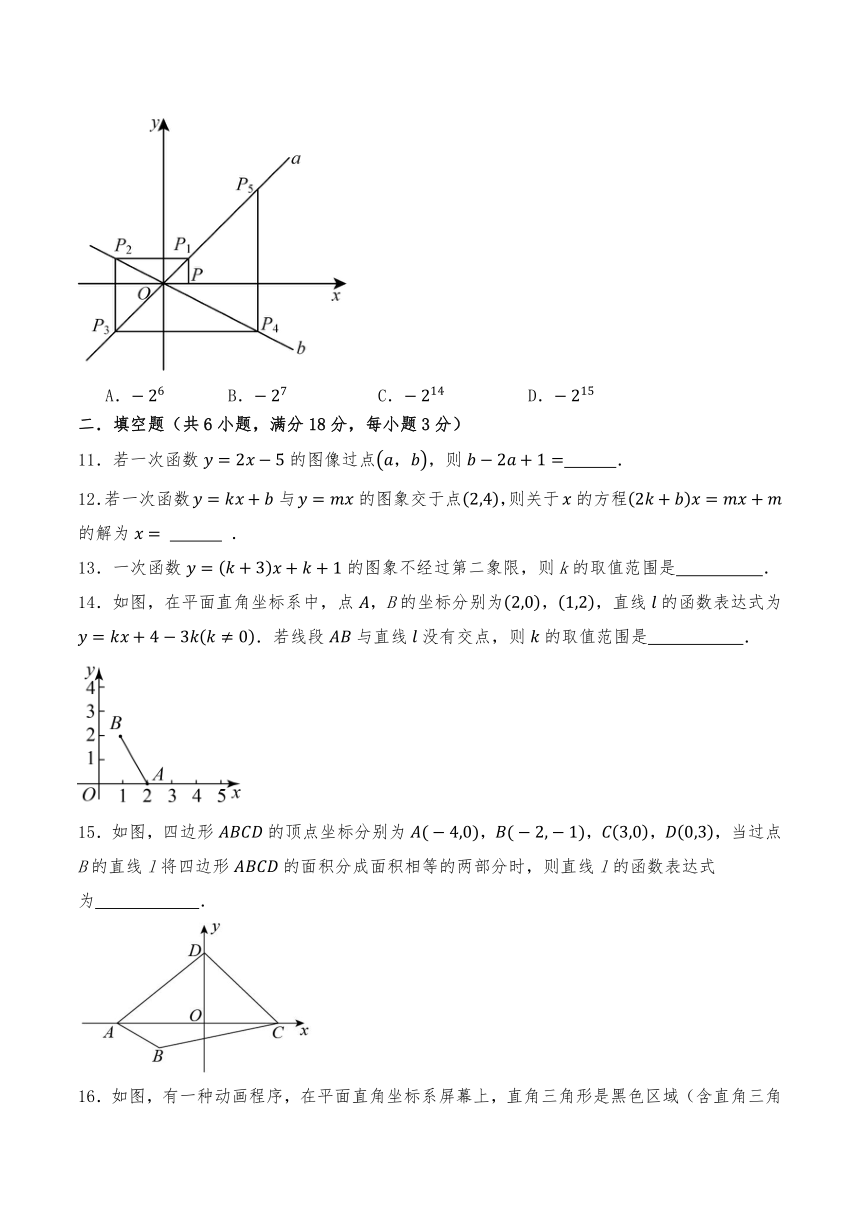
10.如图,已知直线:,直线:和点,过点作轴的平行线交直线于点,过点作轴的平行线,交直线于点,过点作轴的平行线,交直线于点,过点作轴的平行线交直线于点,,按此作法进行下去,则点的横坐标为( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.若一次函数的图像过点,则 .
12.若一次函数与的图象交于点,则关于的方程的解为 .
13.一次函数的图象不经过第二象限,则k的取值范围是 .
14.如图,在平面直角坐标系中,点,B的坐标分别为,,直线的函数表达式为.若线段与直线没有交点,则的取值范围是 .
15.如图,四边形的顶点坐标分别为,,,,当过点B的直线l将四边形的面积分成面积相等的两部分时,则直线l的函数表达式为 .
16.如图,有一种动画程序,在平面直角坐标系屏幕上,直角三角形是黑色区域(含直角三角形边界),其中,,,用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围是 .
三.解答题(共7小题,满分52分)
17.(6分)已知函数.
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围;
(3)若这个函数是一次函数,且图象不经过第四象限,求的取值范围.
18.(6分)已知与x成正比例函数关系,且时,.
(1)写出y与x之间的函数解析式;
(2)求当时,y的值;
(3)求当时,x的值.
19.(8分)已知:同一个坐标系中分别作出了一次函数和的图象,分别与x轴交于点A,B,两直线交于点C.已知点,,,请你观察图象并结合一元一次方程、一元一次不等式和一次函数的相关知识回答下列问题:
(1)关于x的方程的解是_______;关于x的方程的解是________;
(2)请直接写出关于x的不等式的解集;
(3)请直接写出关于x的不等式组的解集.
(4)求的面积.
20.(8分)本市城镇居民年度生活天然气收费标准如下表所示:
阶段 使用量(立方米) 单价(元/立方米)
第一阶段 (含) 3.00
第二阶段 (含) 3.30
第三阶段 超过520 4.20
根据表格信息回答问题:
(1)一同学家2021年度截止到4月已使用328立方米天然气,求至2021年4月,此同学家中使用燃气总共花费多少钱?
(2)试写出缴纳燃气总费用(元)关于燃气使用量(立方米)的函数解析式.
(3)如果该同学家2020年度天然气总缴费1665元,求该同学家2020年度天然气使用总量.
21.(8分)定义:在平面直角坐标系中,函数图象上到两坐标轴的距离之和等于的点,叫做该函数图象的“阶和点”例如,为一次函数的“阶和点”.
(1)若点是关于的正比例函数的“阶和点”,则 ______ , ______ ;
(2)若关于的一次函数的图象经过一次函数图象的“阶和点”,求的值;
(3)若关于的一次函数的图象有且仅有个“阶和点”,求的取值范围.
22.(8分)一艘轮船在航行中遇到暗礁,船身有一处出现进水现象,等到发现时,船内已有一定积水,船员立即开始自救,一边排水一边修船,在整个过程中进水速度不变,同时修船过程中排水速度不变,船修好后不再进水,此时的排水速度与修船过程中进水速度相同,直到将船内积水排尽,设轮船触礁后船舱内积水量为,时间为,y与x之间的函数图象,如图所示.
(1)修船过程中排水速度为 ,a的值为 .
(2)求修船完工后y与x之间的函数关系式,并写出自变量x的取值范围.
(3)当船内积水量是船内最高积水量的时,直接写出x的值.
23.(8分)如图,在平面直角坐标系中,直线l与x轴相交于点P,直线l上的两点,满足,将线段向右平移5个单位长度得到线段.
(1)点C的坐标为_________;
(2)连接,,,点Q是x轴上一点(不与点P重合),连接,交于点E.
①当恰好平分时,试判断与有什么数量关系?并说明理由;
②设点,记三角形的面积为S,三角形的面积为.当时,求点Q的坐标.
答案
一、选择题
1.D
【分析】先根据两直线平行k值相等,以及直线经过点M(0,4),即可求出直线MN的解析式,进而可求出N点坐标,然后根据三角形的面积公式即可求解.
【详解】∵直线与直线平行,
∴k=2,即,
∵直线过点M(0,4),
∴,即b=4,
∴直线MN的解析式为,
当y=0时,有x=-2,
∴N点坐标为(-2,0),
∴ON=2,
∵M(0,4),
∴OM=4,
∴△MON的面积为:,
故选:D.
2.C
【分析】先求得时,,当,直线()与直线平行,且在直线下方;当直线与直线的交点在的上方时,函数()的值都小于函数的值,据此求解即可.
【详解】解:当时,,即有点,
将点代入,
有,解得,
当,直线()与直线平行,且在直线下方;
结合图象可知:直线与直线的交点在的上方时,并随着交点的不断上移,直至直线()与直线平行时,满足当时,函数()的值都小于函数的值,
∴,
故选:C.
3.D
【分析】根据一次函数增减性,结合各选项条件逐项验证即可得到答案.
【详解】解:直线中,
随的增大而减小,
,
,
A、若,则,即与同号(同时为正或同时为负),
,
若取与同为负数,由不能确定的正负,
,为直线上的三个点,
,正负不能确定,则无法判断符号,该选项不合题意;
B、若,则,即与异号(一正一负),
,
,,由不能确定的正负,
,为直线上的三个点,
,正负不能确定,则无法判断符号,该选项不合题意;
C、若,则,即与同号(同时为正或同时为负),
,
若取与同为正数,由不能确定的正负,
,为直线上的三个点,
正负不能确定,正负不能确定,则无法判断符号,该选项不合题意;
D、若,则,即与异号(一正一负),
,
,,由确定的正负,
,为直线上的三个点,
,,则,该选项合题意;
故选:D.
4.D
【分析】①根据一次函数定义即可求解;②,即可求解;③图像经过二、三、四象限,则,,解关于的不等式组即可;④函数图像与轴的交点始终在正半轴,则,即可求解.
【详解】解:①根据一次函数定义:形如的函数为一次函数,
,
,
故①正确;
②,
无论取何值,函数图像必经过点,
故②正确;
③图像经过二、三、四象限,
,
解不等式组得:,
故③正确;
④令,则,
函数图像与轴的交点始终在正半轴,
,
,
经分析知:,
解这个不等式组得,
故④正确.
①②③④都正确.
故选:D.
5.A
【分析】根据“整点”的定义可知,在正方形内(包括边上)扥整点横坐标的取值范围是0到6的自然数,直线在范围时,当,时对应的整点数最多为7个,其次是或时对应的整点数最多为4个,由此即可得到答案.
【详解】解:由画图可知:
,
直线在正方形内(包括边上)经过的整点的个数有7个,
直线在正方形内(包括边上)经过的整点的个数有7个,
直线在正方形内(包括边上)经过的整点的个数有7个,
直线在正方形内(包括边上)经过的整点的个数有4个,
其中点是三条直线、、的交点,点是直线、的交点,
经过的整点的个数最多是:(个),
故选:A.
6.C
【分析】如图:作的高,则为定值.根据三角形的面积公式得出;可判断得到是的正比例函数,最后根据正比例函数的图像与性质即可求解.
【详解】解:如图,作的高,则为定值.
图中阴影部分的面积,即,
为定值,
为定值,
是的正比例函数.
故答案是C.
7.A
【分析】先求出平移过B点的直线解析式,再求出其与x轴的交点坐标,交点记为C,把A点横坐标与C点的横坐标相减即可作答.
【详解】如下图,
过B作x轴垂线,垂足为D,记平移后的直线与x轴的交点为C,
对于直线,令y=0,解得x=4,∴A点坐标为(4,0)
∴OA=4
∵△OAB为等腰直角三角形,BD⊥x轴
∴易得OD=2,BD=2
∴B(2,2);
设平移后的直线为:,把B(2,2)代入得2=1+b,解得b=1,
所以平移后的直线解析式为,令其y=0得
解之得x=-2
∴C(0,-2),
∴OC=2
∴平移的距离为OA+OC=4+2=6.
故选:A.
8.A
【分析】①由函数图象数据可以求出甲的速度,再由追击问题的数量关系建立方程就可以求出乙的速度;
②由函数图象的数据由乙到达终点时走的路程-甲走的路程就可以求出结论;
③乙或甲行驶的路程就是乙追上甲时,两人距A地的距离;
④求出乙到达终点的路程就是A,B两地距离.
【详解】解:①由题意,得
甲的速度为:12÷4=3千米/时;
设乙的速度为a千米/时,由题意,得
(7-4)a=3×7,
解得:a=7.
即乙的速度为7千米/时,
故①正确;
②乙到终点时甲、乙相距的距离为:
(9-4)×7-9×3=8千米,
故②正确;
③当乙追上甲时,两人距A地距离为:
7×3=21千米.
故③正确;
④A,B两地距离为:
7×(9-4)=35千米,
故④错误.
综上所述:错误的只有④.
故选:A.
9.B
【分析】将向右平移1个单位得到点,过点作的垂线,交于点,交于点,当时,符合题意,同理将点向左平移一个单位得到,进而即可求解.
【详解】解:如图,将向右平移1个单位得到点,过点作的垂线,交于点,交于点,当时,符合题意,
,即,
解得
如图,将点向左平移一个单位得到,
,即,
解得
综上所述,,
故选B
10.B
【分析】点,在直线上,得到,求得的纵坐标的纵坐标,得到,即的横坐标为,同理,的横坐标为,的横坐标为,的横坐标为,的横坐标为,的横坐标为,的横坐标为,的横坐标为,,求得的横坐标为,于是得到结论.
【详解】解:∵过点作轴的平行线交直线于点,
∴在直线上,
∴,
∵轴,
∴的纵坐标的纵坐标,
∵在直线上,
∴,
∴,
∴,即的横坐标为,
∵轴,
∴的横坐标为,且在直线上,
∴,
∴,
∵轴,
∴的纵坐标的纵坐标,且在直线上,
∴,
∴,
∴,即的横坐标为,
∵轴,
∴的横坐标为,且在直线上,
即:的横坐标为,
的横坐标为,的横坐标为,
的横坐标为,的横坐标为,
用同样的方法可得:
的横坐标为,的横坐标为,
的横坐标为,的横坐标为,
,
∴的横坐标为,
∴的横坐标为,的横坐标为,
∴的横坐标为,的横坐标为.
故选:B.
二.填空题
11.
【分析】先把点代入一次函数,得到,然后代入代数式计算即可.
【详解】解:∵一次函数的图像过点,
∴,
∴.
故答案为:.
12.1
【分析】由一次函数与的图象交于点得到,代入方程即可求出方程的解.
【详解】解:一次函数与的图象交于点,
当时,,,
,
由得,
,
,
故答案为:.
13.
【分析】已知中,一次函数的图象不经过第二象限,可判断即,且,解之可得k的取值范围.
【详解】解:∵一次函数的图象不经过第二象限,
∴
解得:,
故答案为:.
14.或或
【分析】分别利用当直线过点时,k值最小,当直线过点时,k值最大,即可求出线段与直线有交点时,k的取值范围,据此即可求解.
【详解】解:当直线过点时,k值最小,
则,解得,
当直线过点时,k值最大,
则,解得,
故线段与直线有交点时,k的取值范围为,
故线段与直线没有交点时,k的取值范围为或或,
故答案为:或或.
15.
【分析】先求出四边形ABCD的面积为14,然后根据当直线l与x轴平行时,直线l不能平分四边形ABCD的面积,可设直线l的解析式为,即可求出直线l的解析式为,则直线l与x轴的交点坐标为(,0),求出直线CD的解析式为,则直线l与直线CD的交点坐标为(,),再由过点B的直线l将四边形ABCD的面积分成面积相等的两部分,得到,由此即可得到答案.
【详解】解:∵A(-4,0),B(-2,-1),C(3,0),D(0,3),
∴AC=7,
∴,
∵当直线l与x轴平行时,直线l不能平分四边形ABCD的面积,
∴可设直线l的解析式为,
∴,
∴,
∴直线l的解析式为,
∴直线l与x轴的交点坐标为(,0)
∵点C坐标为(3,0),点D坐标为(0,3),
∴直线CD的解析式为,
∵当时,直线l与直线DC平行,此时直线l不可能平分四边形ABCD的面积
∴联立,
解得,
∴直线l与直线CD的交点坐标为(,),
∵过点B的直线l将四边形ABCD的面积分成面积相等的两部分,
∴,
解得或(舍去),
∴直线l的解析式为 ,
故答案为:.
16.
【分析】根据直线的解析式可知此直线必然经过一三象限,当经过点B时b的值最小,当经过点C时b的值最大,由此可得出结论.
【详解】解:∵直线中,,
∴此直线必然经过一三象限.
∵,,,
∴当经过点B时,,解得;
当经过点C时,,解得,
∴.
故答案为:.
三.解答题
17.(1)解:把代入,得
,
解得∶;
(2)解:∵随的增大而减小,
∴,
解得:;
(3)解:∵函数是一次函数,且图象不经过第四象限,即:,,
解得:.
18.(1)解:依题意得:设.
将代入:得
所以,.
(2)由(1)知,,
∴当时,,即;
(3)由(1)知,,
∴当时,,
解得,.
19.(1)∵一次函数和的图象,分别与轴交于,,
∴关于的方程的解是;
关于的方程的解是;
(2)∵一次函数和的图象交于点
∴根据图象可以得到:关于的不等式的解集为;
(3)根据图象可以得到:关于的不等式的解集为,
关于的不等式的解集为
∴关于的不等式组的解集为;
(4)∵,,
∴
∴的面积.
20.(1)解:由题意得:(元),
答:此同学家中使用燃气总共花费元;
(2)解:由题意得:;
(3)解:由(2)知,,
当时,,
∵,
∴该同学家2020年度天然气总使用量超过了520立方米,
(立方米),
答:该同学家2020年度天然气使用总量为立方米.
21.(1)解:点是关于的正比例函数的点,
,
,
点到两坐标轴的距离之和等于,
点是关于的正比例函数的“阶和点”,
.
故答案为:;;
(2)设一次函数图象的“阶和点”为,则,,
一次函数图象经过第一、二、三象限,
当在第一象限时,,
,,
一次函数图象的“阶和点”为,
,
;
当在第二象限时,,由于,此种情形不存在;
当在第三象限时,,
,,
一次函数图象的“阶和点”为,
,
.
综上,关于的一次函数的图象经过一次函数图象的“阶和点”,的值为或;
(3)由题意得:,
,
关于的一次函数的图象经过第一、三、四象限,
设为关于的一次函数的图象的“阶和点”,
,
当在第一象限时,,
,
,
,
,,
,符合题意,
当在第一象限时,;
当在第三象限时,,
,
,
,
,
,
;
当在第三象限时,;
当在第四象限时,,
,
,
.
当在第四象限时,.
关于的一次函数的图象有且仅有个“阶和点”,
以上三个条件中同时满足其中两个即可,
当满足不满足时,;
当满足不满足时,;
当满足不满足时,的值不存在,
综上,关于的一次函数的图象有且仅有个“阶和点”,的取值范围为或.
22.(1)解:进水速度为:,
排水速度为:,
∵船修好后不再进水,此时的排水速度与修船过程中进水速度相同,
∴;
故答案为:1;24.
(2)解:设修船完工后y与x之间的函数关系式为,根据题意得:
,
解得:,
∴修船完工后y与x之间的函数关系式为;
(3)解:设修船过程中y与x之间的函数关系式为,根据题意得:
,
解得:,
∴修船过程中y与x之间的函数关系式为
当修船过程中,船内积水量是船内最高积水量的时,根据题意得:
,
解得:;
当船修好后不再进水,船内积水量是船内最高积水量的时,根据题意得:
,
解得:;
综上分析可知,当或时,船内积水量是船内最高积水量的.
23.(1)解: ,
,,
,,
,,
B向右平移5个单位得到C,
故答案为:.
(2)①.理由如下:
平分,
,
向右平移5个单位得到CD,
,
,
.
②令直线l的解析式为,
,在直线l上,
,解得
直线l的解析式为,
当时,
,,
,
如图,连接,
,,,,
,
,
解得或
点坐标为或.
一.选择题(共10小题,满分30分,每小题3分)
1.在平面直角坐标系中,已知直线与直线平行,且与轴交于点,与轴的交点为,则的面积为( )
A.2022 B.1011 C.8 D.4
2.当时,对于x的每一个值,函数(k≠0)的值都小于函数的值,则k的取值范围是( )
A.且 B. C. D.
3.已知,,为直线上的三个点,且,则以下判断正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
4.关于函数(为常数),有下列结论:①当时,此函数是一次函数;②无论取什么值,函数图像必经过点;③若图像经过二、三、四象限,则的取值范围是;④若函数图像与轴的交点始终在正半轴,则的取值范围是.其中,正确结论的个数是( ).
A.1 B.2 C.3 D.4
5.若平面直角坐标系内的点满足横,纵坐标都为整数,则把点叫做“整点”,例如,,都是“整点”,四边形(为原点)为正方形且点坐标为,有4条直线,其中,,,互不相等,则这4条直线在正方形内(包括边上)经过的整点个数最多是( )个.
A.22 B.24 C.28 D.25
6.如图,在中,点是边上一点,点从点出发沿向点运动,到达点时停止.若,图中阴影部分面积为,则图中可以近似地刻画出与之间关系的是( )
B.
C. D.
7.如图,直线与轴交于点,以为斜边在轴上方作等腰直角三角形,将直线沿轴向左平移,当点落在平移后的直线上时,则直线平移的距离是( )
A.6 B.5 C.4 D.3
8.甲乙两人在同一条笔直的公路上步行从A地去往B地,已知甲、乙两人保持各自的速度匀速步行,且甲先出发,甲乙两人的距离(千米)与甲步行的时间(小时)的函数关系图像如图所示,下列说法:
①乙的速度为千米/时;
②乙到终点时甲、乙相距千米;
③当乙追上甲时,两人距地千米;
④两地距离为千米.
其中错误的个数为( )
A.1个 B.2个 C.3个 D.4个
9.如图,分别是直线上的动点,若时,都有,则的取值范围为( )
A. B. C. D.
10.如图,已知直线:,直线:和点,过点作轴的平行线交直线于点,过点作轴的平行线,交直线于点,过点作轴的平行线,交直线于点,过点作轴的平行线交直线于点,,按此作法进行下去,则点的横坐标为( )
A. B. C. D.
二.填空题(共6小题,满分18分,每小题3分)
11.若一次函数的图像过点,则 .
12.若一次函数与的图象交于点,则关于的方程的解为 .
13.一次函数的图象不经过第二象限,则k的取值范围是 .
14.如图,在平面直角坐标系中,点,B的坐标分别为,,直线的函数表达式为.若线段与直线没有交点,则的取值范围是 .
15.如图,四边形的顶点坐标分别为,,,,当过点B的直线l将四边形的面积分成面积相等的两部分时,则直线l的函数表达式为 .
16.如图,有一种动画程序,在平面直角坐标系屏幕上,直角三角形是黑色区域(含直角三角形边界),其中,,,用信号枪沿直线发射信号,当信号遇到黑色区域时,区域便由黑变白,则能够使黑色区域变白的b的取值范围是 .
三.解答题(共7小题,满分52分)
17.(6分)已知函数.
(1)若函数图象经过原点,求的值;
(2)若这个函数是一次函数,且随着的增大而减小,求的取值范围;
(3)若这个函数是一次函数,且图象不经过第四象限,求的取值范围.
18.(6分)已知与x成正比例函数关系,且时,.
(1)写出y与x之间的函数解析式;
(2)求当时,y的值;
(3)求当时,x的值.
19.(8分)已知:同一个坐标系中分别作出了一次函数和的图象,分别与x轴交于点A,B,两直线交于点C.已知点,,,请你观察图象并结合一元一次方程、一元一次不等式和一次函数的相关知识回答下列问题:
(1)关于x的方程的解是_______;关于x的方程的解是________;
(2)请直接写出关于x的不等式的解集;
(3)请直接写出关于x的不等式组的解集.
(4)求的面积.
20.(8分)本市城镇居民年度生活天然气收费标准如下表所示:
阶段 使用量(立方米) 单价(元/立方米)
第一阶段 (含) 3.00
第二阶段 (含) 3.30
第三阶段 超过520 4.20
根据表格信息回答问题:
(1)一同学家2021年度截止到4月已使用328立方米天然气,求至2021年4月,此同学家中使用燃气总共花费多少钱?
(2)试写出缴纳燃气总费用(元)关于燃气使用量(立方米)的函数解析式.
(3)如果该同学家2020年度天然气总缴费1665元,求该同学家2020年度天然气使用总量.
21.(8分)定义:在平面直角坐标系中,函数图象上到两坐标轴的距离之和等于的点,叫做该函数图象的“阶和点”例如,为一次函数的“阶和点”.
(1)若点是关于的正比例函数的“阶和点”,则 ______ , ______ ;
(2)若关于的一次函数的图象经过一次函数图象的“阶和点”,求的值;
(3)若关于的一次函数的图象有且仅有个“阶和点”,求的取值范围.
22.(8分)一艘轮船在航行中遇到暗礁,船身有一处出现进水现象,等到发现时,船内已有一定积水,船员立即开始自救,一边排水一边修船,在整个过程中进水速度不变,同时修船过程中排水速度不变,船修好后不再进水,此时的排水速度与修船过程中进水速度相同,直到将船内积水排尽,设轮船触礁后船舱内积水量为,时间为,y与x之间的函数图象,如图所示.
(1)修船过程中排水速度为 ,a的值为 .
(2)求修船完工后y与x之间的函数关系式,并写出自变量x的取值范围.
(3)当船内积水量是船内最高积水量的时,直接写出x的值.
23.(8分)如图,在平面直角坐标系中,直线l与x轴相交于点P,直线l上的两点,满足,将线段向右平移5个单位长度得到线段.
(1)点C的坐标为_________;
(2)连接,,,点Q是x轴上一点(不与点P重合),连接,交于点E.
①当恰好平分时,试判断与有什么数量关系?并说明理由;
②设点,记三角形的面积为S,三角形的面积为.当时,求点Q的坐标.
答案
一、选择题
1.D
【分析】先根据两直线平行k值相等,以及直线经过点M(0,4),即可求出直线MN的解析式,进而可求出N点坐标,然后根据三角形的面积公式即可求解.
【详解】∵直线与直线平行,
∴k=2,即,
∵直线过点M(0,4),
∴,即b=4,
∴直线MN的解析式为,
当y=0时,有x=-2,
∴N点坐标为(-2,0),
∴ON=2,
∵M(0,4),
∴OM=4,
∴△MON的面积为:,
故选:D.
2.C
【分析】先求得时,,当,直线()与直线平行,且在直线下方;当直线与直线的交点在的上方时,函数()的值都小于函数的值,据此求解即可.
【详解】解:当时,,即有点,
将点代入,
有,解得,
当,直线()与直线平行,且在直线下方;
结合图象可知:直线与直线的交点在的上方时,并随着交点的不断上移,直至直线()与直线平行时,满足当时,函数()的值都小于函数的值,
∴,
故选:C.
3.D
【分析】根据一次函数增减性,结合各选项条件逐项验证即可得到答案.
【详解】解:直线中,
随的增大而减小,
,
,
A、若,则,即与同号(同时为正或同时为负),
,
若取与同为负数,由不能确定的正负,
,为直线上的三个点,
,正负不能确定,则无法判断符号,该选项不合题意;
B、若,则,即与异号(一正一负),
,
,,由不能确定的正负,
,为直线上的三个点,
,正负不能确定,则无法判断符号,该选项不合题意;
C、若,则,即与同号(同时为正或同时为负),
,
若取与同为正数,由不能确定的正负,
,为直线上的三个点,
正负不能确定,正负不能确定,则无法判断符号,该选项不合题意;
D、若,则,即与异号(一正一负),
,
,,由确定的正负,
,为直线上的三个点,
,,则,该选项合题意;
故选:D.
4.D
【分析】①根据一次函数定义即可求解;②,即可求解;③图像经过二、三、四象限,则,,解关于的不等式组即可;④函数图像与轴的交点始终在正半轴,则,即可求解.
【详解】解:①根据一次函数定义:形如的函数为一次函数,
,
,
故①正确;
②,
无论取何值,函数图像必经过点,
故②正确;
③图像经过二、三、四象限,
,
解不等式组得:,
故③正确;
④令,则,
函数图像与轴的交点始终在正半轴,
,
,
经分析知:,
解这个不等式组得,
故④正确.
①②③④都正确.
故选:D.
5.A
【分析】根据“整点”的定义可知,在正方形内(包括边上)扥整点横坐标的取值范围是0到6的自然数,直线在范围时,当,时对应的整点数最多为7个,其次是或时对应的整点数最多为4个,由此即可得到答案.
【详解】解:由画图可知:
,
直线在正方形内(包括边上)经过的整点的个数有7个,
直线在正方形内(包括边上)经过的整点的个数有7个,
直线在正方形内(包括边上)经过的整点的个数有7个,
直线在正方形内(包括边上)经过的整点的个数有4个,
其中点是三条直线、、的交点,点是直线、的交点,
经过的整点的个数最多是:(个),
故选:A.
6.C
【分析】如图:作的高,则为定值.根据三角形的面积公式得出;可判断得到是的正比例函数,最后根据正比例函数的图像与性质即可求解.
【详解】解:如图,作的高,则为定值.
图中阴影部分的面积,即,
为定值,
为定值,
是的正比例函数.
故答案是C.
7.A
【分析】先求出平移过B点的直线解析式,再求出其与x轴的交点坐标,交点记为C,把A点横坐标与C点的横坐标相减即可作答.
【详解】如下图,
过B作x轴垂线,垂足为D,记平移后的直线与x轴的交点为C,
对于直线,令y=0,解得x=4,∴A点坐标为(4,0)
∴OA=4
∵△OAB为等腰直角三角形,BD⊥x轴
∴易得OD=2,BD=2
∴B(2,2);
设平移后的直线为:,把B(2,2)代入得2=1+b,解得b=1,
所以平移后的直线解析式为,令其y=0得
解之得x=-2
∴C(0,-2),
∴OC=2
∴平移的距离为OA+OC=4+2=6.
故选:A.
8.A
【分析】①由函数图象数据可以求出甲的速度,再由追击问题的数量关系建立方程就可以求出乙的速度;
②由函数图象的数据由乙到达终点时走的路程-甲走的路程就可以求出结论;
③乙或甲行驶的路程就是乙追上甲时,两人距A地的距离;
④求出乙到达终点的路程就是A,B两地距离.
【详解】解:①由题意,得
甲的速度为:12÷4=3千米/时;
设乙的速度为a千米/时,由题意,得
(7-4)a=3×7,
解得:a=7.
即乙的速度为7千米/时,
故①正确;
②乙到终点时甲、乙相距的距离为:
(9-4)×7-9×3=8千米,
故②正确;
③当乙追上甲时,两人距A地距离为:
7×3=21千米.
故③正确;
④A,B两地距离为:
7×(9-4)=35千米,
故④错误.
综上所述:错误的只有④.
故选:A.
9.B
【分析】将向右平移1个单位得到点,过点作的垂线,交于点,交于点,当时,符合题意,同理将点向左平移一个单位得到,进而即可求解.
【详解】解:如图,将向右平移1个单位得到点,过点作的垂线,交于点,交于点,当时,符合题意,
,即,
解得
如图,将点向左平移一个单位得到,
,即,
解得
综上所述,,
故选B
10.B
【分析】点,在直线上,得到,求得的纵坐标的纵坐标,得到,即的横坐标为,同理,的横坐标为,的横坐标为,的横坐标为,的横坐标为,的横坐标为,的横坐标为,的横坐标为,,求得的横坐标为,于是得到结论.
【详解】解:∵过点作轴的平行线交直线于点,
∴在直线上,
∴,
∵轴,
∴的纵坐标的纵坐标,
∵在直线上,
∴,
∴,
∴,即的横坐标为,
∵轴,
∴的横坐标为,且在直线上,
∴,
∴,
∵轴,
∴的纵坐标的纵坐标,且在直线上,
∴,
∴,
∴,即的横坐标为,
∵轴,
∴的横坐标为,且在直线上,
即:的横坐标为,
的横坐标为,的横坐标为,
的横坐标为,的横坐标为,
用同样的方法可得:
的横坐标为,的横坐标为,
的横坐标为,的横坐标为,
,
∴的横坐标为,
∴的横坐标为,的横坐标为,
∴的横坐标为,的横坐标为.
故选:B.
二.填空题
11.
【分析】先把点代入一次函数,得到,然后代入代数式计算即可.
【详解】解:∵一次函数的图像过点,
∴,
∴.
故答案为:.
12.1
【分析】由一次函数与的图象交于点得到,代入方程即可求出方程的解.
【详解】解:一次函数与的图象交于点,
当时,,,
,
由得,
,
,
故答案为:.
13.
【分析】已知中,一次函数的图象不经过第二象限,可判断即,且,解之可得k的取值范围.
【详解】解:∵一次函数的图象不经过第二象限,
∴
解得:,
故答案为:.
14.或或
【分析】分别利用当直线过点时,k值最小,当直线过点时,k值最大,即可求出线段与直线有交点时,k的取值范围,据此即可求解.
【详解】解:当直线过点时,k值最小,
则,解得,
当直线过点时,k值最大,
则,解得,
故线段与直线有交点时,k的取值范围为,
故线段与直线没有交点时,k的取值范围为或或,
故答案为:或或.
15.
【分析】先求出四边形ABCD的面积为14,然后根据当直线l与x轴平行时,直线l不能平分四边形ABCD的面积,可设直线l的解析式为,即可求出直线l的解析式为,则直线l与x轴的交点坐标为(,0),求出直线CD的解析式为,则直线l与直线CD的交点坐标为(,),再由过点B的直线l将四边形ABCD的面积分成面积相等的两部分,得到,由此即可得到答案.
【详解】解:∵A(-4,0),B(-2,-1),C(3,0),D(0,3),
∴AC=7,
∴,
∵当直线l与x轴平行时,直线l不能平分四边形ABCD的面积,
∴可设直线l的解析式为,
∴,
∴,
∴直线l的解析式为,
∴直线l与x轴的交点坐标为(,0)
∵点C坐标为(3,0),点D坐标为(0,3),
∴直线CD的解析式为,
∵当时,直线l与直线DC平行,此时直线l不可能平分四边形ABCD的面积
∴联立,
解得,
∴直线l与直线CD的交点坐标为(,),
∵过点B的直线l将四边形ABCD的面积分成面积相等的两部分,
∴,
解得或(舍去),
∴直线l的解析式为 ,
故答案为:.
16.
【分析】根据直线的解析式可知此直线必然经过一三象限,当经过点B时b的值最小,当经过点C时b的值最大,由此可得出结论.
【详解】解:∵直线中,,
∴此直线必然经过一三象限.
∵,,,
∴当经过点B时,,解得;
当经过点C时,,解得,
∴.
故答案为:.
三.解答题
17.(1)解:把代入,得
,
解得∶;
(2)解:∵随的增大而减小,
∴,
解得:;
(3)解:∵函数是一次函数,且图象不经过第四象限,即:,,
解得:.
18.(1)解:依题意得:设.
将代入:得
所以,.
(2)由(1)知,,
∴当时,,即;
(3)由(1)知,,
∴当时,,
解得,.
19.(1)∵一次函数和的图象,分别与轴交于,,
∴关于的方程的解是;
关于的方程的解是;
(2)∵一次函数和的图象交于点
∴根据图象可以得到:关于的不等式的解集为;
(3)根据图象可以得到:关于的不等式的解集为,
关于的不等式的解集为
∴关于的不等式组的解集为;
(4)∵,,
∴
∴的面积.
20.(1)解:由题意得:(元),
答:此同学家中使用燃气总共花费元;
(2)解:由题意得:;
(3)解:由(2)知,,
当时,,
∵,
∴该同学家2020年度天然气总使用量超过了520立方米,
(立方米),
答:该同学家2020年度天然气使用总量为立方米.
21.(1)解:点是关于的正比例函数的点,
,
,
点到两坐标轴的距离之和等于,
点是关于的正比例函数的“阶和点”,
.
故答案为:;;
(2)设一次函数图象的“阶和点”为,则,,
一次函数图象经过第一、二、三象限,
当在第一象限时,,
,,
一次函数图象的“阶和点”为,
,
;
当在第二象限时,,由于,此种情形不存在;
当在第三象限时,,
,,
一次函数图象的“阶和点”为,
,
.
综上,关于的一次函数的图象经过一次函数图象的“阶和点”,的值为或;
(3)由题意得:,
,
关于的一次函数的图象经过第一、三、四象限,
设为关于的一次函数的图象的“阶和点”,
,
当在第一象限时,,
,
,
,
,,
,符合题意,
当在第一象限时,;
当在第三象限时,,
,
,
,
,
,
;
当在第三象限时,;
当在第四象限时,,
,
,
.
当在第四象限时,.
关于的一次函数的图象有且仅有个“阶和点”,
以上三个条件中同时满足其中两个即可,
当满足不满足时,;
当满足不满足时,;
当满足不满足时,的值不存在,
综上,关于的一次函数的图象有且仅有个“阶和点”,的取值范围为或.
22.(1)解:进水速度为:,
排水速度为:,
∵船修好后不再进水,此时的排水速度与修船过程中进水速度相同,
∴;
故答案为:1;24.
(2)解:设修船完工后y与x之间的函数关系式为,根据题意得:
,
解得:,
∴修船完工后y与x之间的函数关系式为;
(3)解:设修船过程中y与x之间的函数关系式为,根据题意得:
,
解得:,
∴修船过程中y与x之间的函数关系式为
当修船过程中,船内积水量是船内最高积水量的时,根据题意得:
,
解得:;
当船修好后不再进水,船内积水量是船内最高积水量的时,根据题意得:
,
解得:;
综上分析可知,当或时,船内积水量是船内最高积水量的.
23.(1)解: ,
,,
,,
,,
B向右平移5个单位得到C,
故答案为:.
(2)①.理由如下:
平分,
,
向右平移5个单位得到CD,
,
,
.
②令直线l的解析式为,
,在直线l上,
,解得
直线l的解析式为,
当时,
,,
,
如图,连接,
,,,,
,
,
解得或
点坐标为或.
