八年级数学上册试题 第13章《三角形中的边角关系、命题与证明》章节测试卷-沪科版(含解析)
文档属性
| 名称 | 八年级数学上册试题 第13章《三角形中的边角关系、命题与证明》章节测试卷-沪科版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 911.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 08:12:39 | ||
图片预览


文档简介
第13章《三角形中的边角关系、命题与证明》章节测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列实际情景运用了三角形稳定性的是( )
A.人能直立在地面上 B.校门口的自动伸缩栅栏门
C.古建筑中的三角形屋架 D.三轮车能在地面上运动而不会倒
2.如图,的三边长均为整数,且周长为,是边上的中线,的周长比的周长大2,则长的可能值有( )个.
A. B.
C. D.
3.下列命题是假命题的是( )
A.如果,,那么
B.对顶角相等
C.如果一个数能被整除,那么它肯定也能被整除
D.内错角相等
4.如图所示,∠F=90°,CE⊥AB,C是BF的中点,D是BE上的一点,下列说法正确的是( )
A.CD是△ABC的中线 B.AF是△ABC的高
C.CE是△ABF的中位线 D.AC是△ABF的角平分线
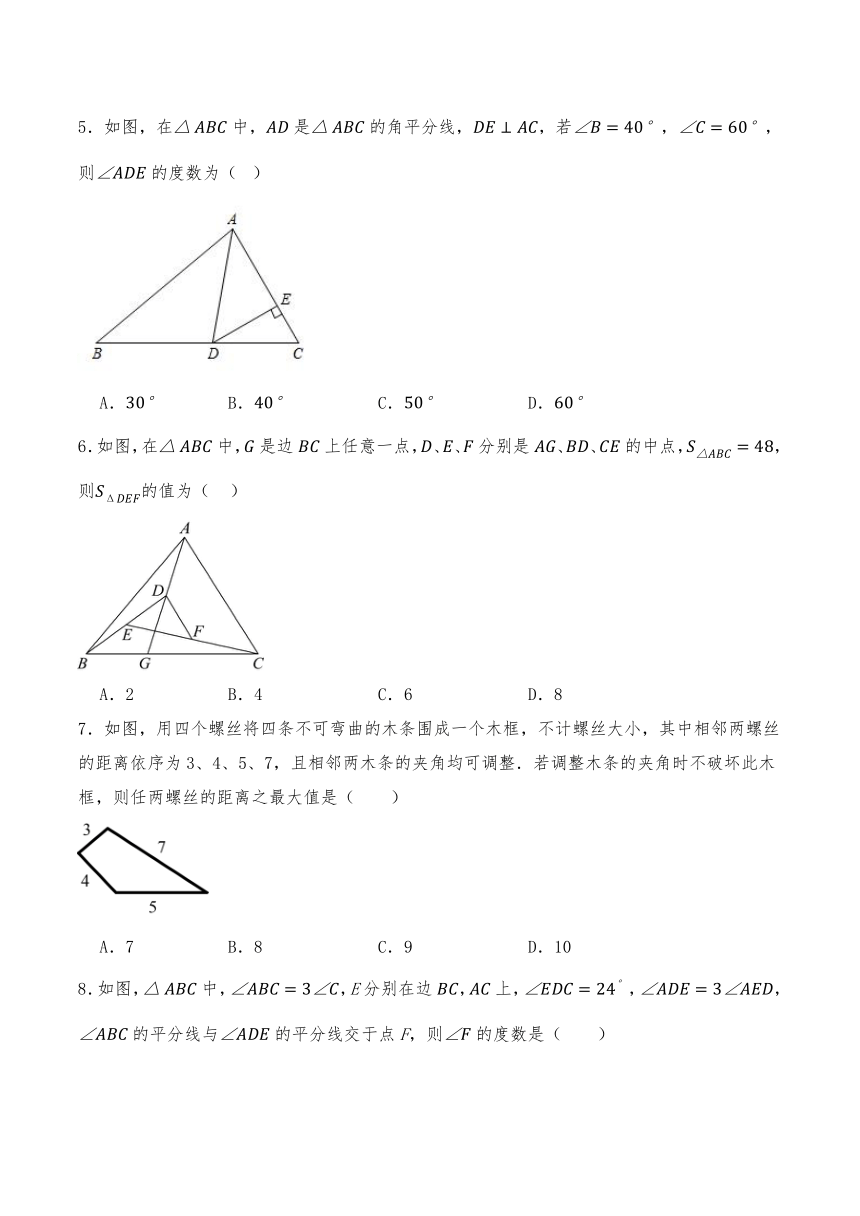
5.如图,在中,是的角平分线,,若,,则的度数为( )
A. B. C. D.
6.如图,在中,是边上任意一点,、、分别是、、的中点,,则的值为( )
A.2 B.4 C.6 D.8
7.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为3、4、5、7,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值是( )
A.7 B.8 C.9 D.10
8.如图,中,,E分别在边,上,,,的平分线与的平分线交于点F,则的度数是( )
A.54° B.60° C.66° D.72°
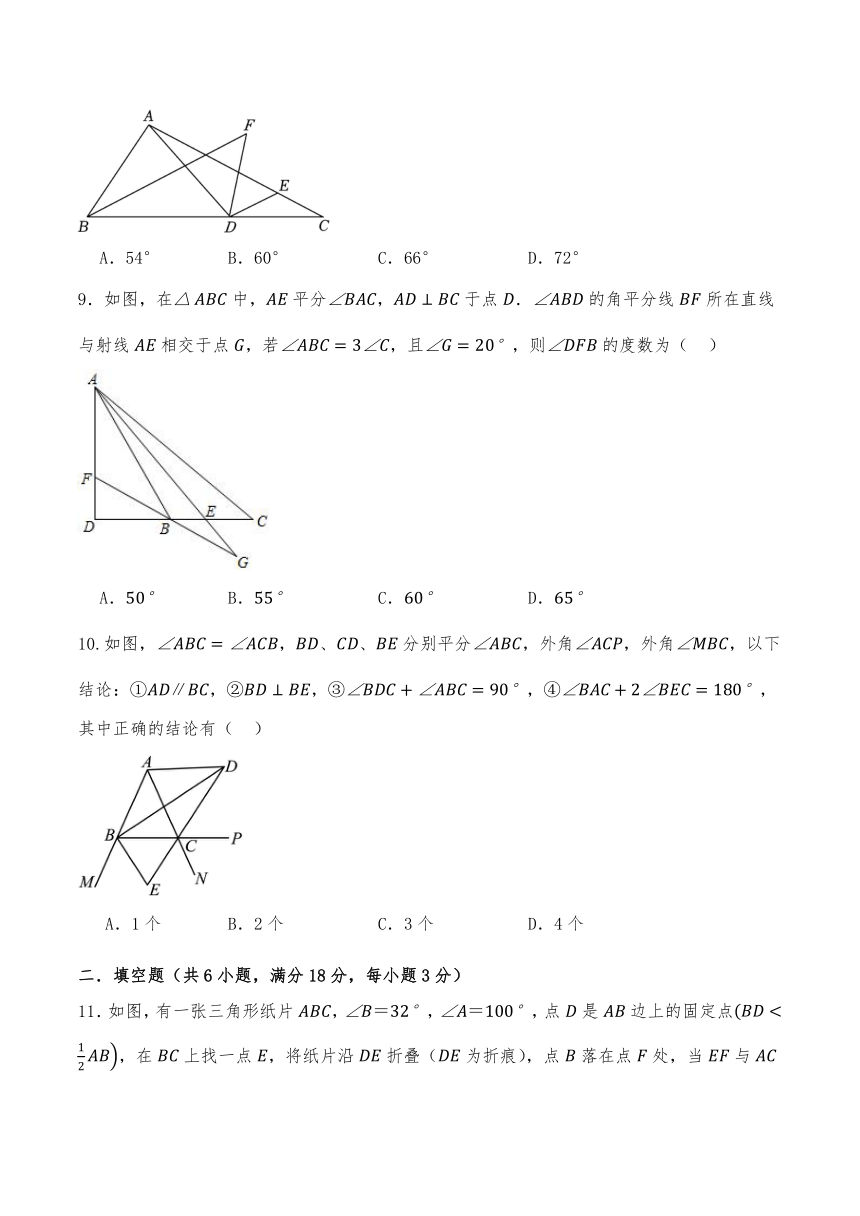
9.如图,在中,平分,于点.的角平分线所在直线与射线相交于点,若,且,则的度数为( )
A. B. C. D.
10.如图,,、、分别平分,外角,外角,以下结论:①,②,③,④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分,每小题3分)
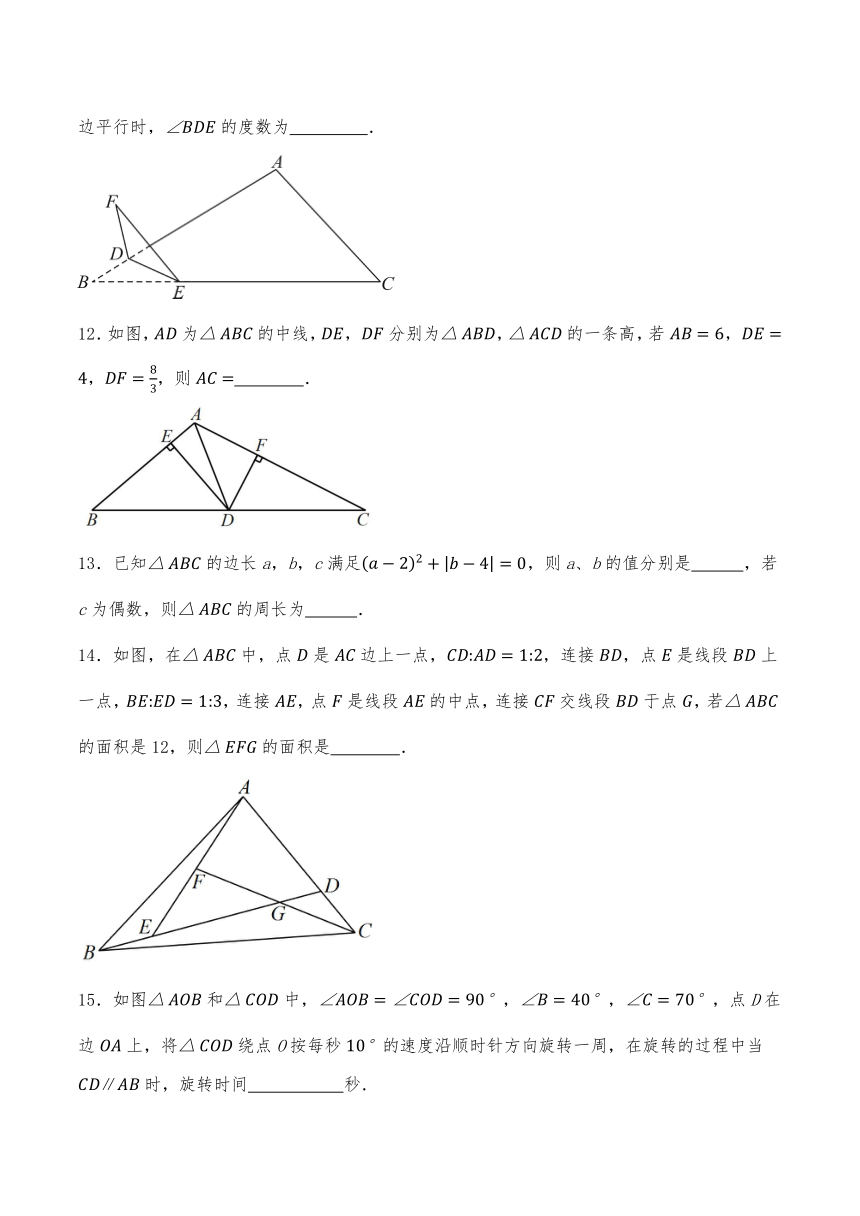
11.如图,有一张三角形纸片,,,点是边上的固定点,在上找一点,将纸片沿折叠(为折痕),点落在点处,当与边平行时,的度数为 .
12.如图,为的中线,分别为,的一条高,若,则 .
13.已知的边长a,b,c满足,则a、b的值分别是 ,若c为偶数,则的周长为 .
14.如图,在中,点是边上一点,,连接,点是线段上一点,,连接,点是线段的中点,连接交线段于点,若的面积是12,则的面积是 .
15.如图和中,,,,点D在边上,将绕点O按每秒的速度沿顺时针方向旋转一周,在旋转的过程中当时,旋转时间 秒.
16.如果三角形中任意两个内角与满足,那么我们称这样的三角形为“斜等边三角形”.在锐角三角形中,于点D,若、、都是“斜等边三角形”,则 .
三.解答题(共7小题,满分52分)
17.(6分)(1)一个多边形的内角和是外角和的3倍,这个多边形是几边形?
(2)小明求得一个多边形的内角和为,小强很快发现小明所得的度数有误,后来小明复查时发现他重复加了一个内角,求出这个多边形的边数以及他重复加的那个角的度数.
18.(6分)如图所示,D是△ABC的边AC上任意一点(不含端点),连结BD,请判断AB+BC+AC与2BD的大小关系,并说明理由.
19.(8分)在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示.将平移,使点C平移至点D,点A、B的对应点分别是点E、F.
(1)在图中请画出平移后得到的;
(2)在图中画出的边上的高;
(3)若连接,则这两条线段之间的关系是 ;
(4)的面积为 .
20.(8分)如图所示,已知,分别是的高和中线,,,,.
(1)求的长;
(2)求和周长的差.
21.(8分)在中,,均为锐角且不相等,线段是中边上的高,是的角平分线.
(1)如图1,,,求的度数;
(2)若,,则______;
(3)是射线上一动点,C、H分别为线段A,上的点(不与端点重合),将沿着折叠,使点B落到点F处,如图2所示,请直接写出,与的数量关系.
22.(8分)已知,在中,,点在上,过点的一条直线与直线、分别交于点、.
(1)如图1,,则______°.
(2)如图2,猜想、、之间的数量关系,并加以证明;
(3)如图3,直接写出、、之间的数量关系______.
23.(8分)将含角的三角板()和含角的三角板及一把直尺按图方式摆放在起.使两块三角板的直角顶点,重合.点,,,始终落在直尺的边所在直线上.将含角的三角板沿直线向右平移.
(1)当点与点重合,请在备用图中补全图形,并求平移后与形成的夹角的度数;
(2)如图,点在线段上移动,是边上的动点,满足被平分,的平分线与边交于点,请证明在移动过程中,的大小保持不变;
(3)仿照(2)的探究,点在射线上移动,是边上的动点,满足被平分,的平分线所在直线与直线交于点,请写出一个与平移过程有关的合理猜想.(不用证明)
答案
一.选择题
1.C
【分析】根据三角形的稳定性进行判断即可求解.
【详解】解:古建筑中的三角形屋架是利用了三角形的稳定性,
故选C
2.B
【分析】依据的周长为22,的周长比的周长大2,可得,再根据的三边长均为整数,即可得到,6,8,10.
【详解】解:的周长为22,的周长比的周长大2,
,
解得,
又的三边长均为整数,的周长比的周长大2,
为整数,
边长为偶数,
,6,8,10,
即的长可能值有4个,
故选:B.
3.D
【分析】利用对顶角的性质、实数的性质、平行线的性质分别判断后即可确定正确的选项.
【详解】解:、如果,,那么,正确,是真命题,故本选项不符合题意;
、对顶角相等,正确,是真命题,故本选项不符合题意;
、如果一个数能被整除,那么它肯定也能被整除,正确,是真命题,故本选项不符合题意;
、两直线平行,内错角相等,原命题是假命题,故本选项符合题意.
故选:.
4.B
【分析】根据三角形中位线的定义,三角形角平分线、中线和高的定义作答.
【详解】解:A、AC是△ABC的中线,故本选项不符合题意.
B、由∠F=90°知,AF是△ABC的高,故本选项符合题意.
C、CE是△ABC的高,故本选项不符合题意.
D、AC是△ABF的中线,故本选项不符合题意.
故选:B.
5.C
【分析】根据三角形内角和定理求出,再根据角平分线的定义可得,最后利用垂线的定义可得,进而解答即可.
【详解】解:∵,
∴.
∵平分,
∴.
∵,
∴,
∴.
故选C.
6.C
【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.
【详解】解:连接,如图所示:
∵点D是的中点,
∴,
∴,
∴,
∵点E是的中点,
∴,
∵点F是的中点,
∴.
故选:C.
7.C
【分析】若两螺丝的距离最大,则此时这个木框的形状为三角形,根据三角形任意两边之和大于第三边,进行求解即可.
【详解】解:①当、在一条直线上时,三边长为:、、,
此时最大距离为;
②,
、不可能在一条直线上;
③当、在一条直线上时,三边长为:、、,
此时最大距离为;
④,
、不可能在一条直线上;
综上所述:最大距离为.
故选:C.
8.B
【分析】根据题意可知,设,表示出,根据角平分线的定义,可得的度数,根据列方程,即可求出的度数.
【详解】解:∵平分,
∴,
∵,
∴,
设,则,
∵,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴,
∴.
故选:B.
9.C
【分析】由角平分线的定义可以得到,,设,假设,,通过角的等量代换可得到,代入的值即可.
【详解】∵平分,平分
∴,
设
∵
∴可以假设,
∴
∵
∴
∴
设,则
∴
∴
∵
∴
故答案选:C
10.D
【分析】根据角平分线的定义、三角形的内角和定理、三角形的外角性质、平行线的判定一一判定即可.
【详解】解:①设点A、B在直线上,
∵、分别平分的内角,外角,
∴平分的外角,
∴,
∵,且,
∴,
∴,故①正确.
②∵、分别平分的内角、外角,
∴,
∴,故②正确.
③∵,,
∴,
∴,
∵,
∴,
∴,故③正确.
④∵
∴,
∴,故④正确.
故选:D.
二.填空题
11.
【分析】根据已知、折叠和平行线,得,再计算的度数,最后根据三角形内角和为计算的度数即可.
【详解】,,,
(两直线平行,同位角相等),
纸片沿折叠(为折痕),点落在点处,
,
(三角形内角和为),
故答案为:.
12.9
【分析】由为的中线得,从而得到,代入进行计算即可得到答案.
【详解】解: 为的中线,
,
,
分别为,的一条高,
,
,
,
故答案为:9.
13. 2、4 10
【分析】由,可得,,解得,,由三角形三边关系可得,,即,由c为偶数,可得,然后求周长即可.
【详解】解:∵,
∴,,
解得,,
由三角形三边关系可得,,即,
∵c为偶数,
∴,
∴的周长为,
故答案为:2、4,10.
14.
【分析】连接,.由题意中的线段的比和,可推出,,从而可求出,.结合中点的性质即得出,从而可求出,进而得出,最后即得出,最后即可求出.
【详解】解:如图,连接,.
∵,,
∴,.
又∵,
∴,.
∵点是线段的中点,
∴.
∵,
∴,
∴,
∴,
∴,即,
∴,
∴.
故答案为:.
15.11或29
【分析】根据题意,画出图形,进行分类讨论,①当点C在内时,根据三角形的内角和定理可得,根据平行线的性质得出,再根据三角形的外角定理求出,进而得出,即可求解;②当点C在外时,延长交于一点,根据平行线的性质得出,再根据三角形的外角定理求出 ,即可得出,即可求解.
【详解】解:①当点C在内时,如图,
在中,,
∴,
∵,,
∴,
∵,
∴,
∴,
∴旋转时间(秒),
②当点C在外时,延长交于一点,如图,
∵,,
∴,
由①可得,,
∴,
∴,
∴绕点O沿顺时针方向旋转了,
∴旋转时间(秒),
故答案为:11或29.
16.
【分析】根据新定义的“斜等边三角形”的特点分情况分析,然后利用三角形内角和定理求解即可.
【详解】解:是“斜等边三角形”, ,
∴
(1),
∵,
∴解得:,;
(2),
∴解得:,;
(3),
∵,
∴解得:,;
(4),
∴解得:,;
是“斜等边三角形”,
①,
∵,
∴解得:,;
②,
∴解得:,;
③,
∵,
∴解得:,;
④,
∴解得:,;
当(1)①成立时,,,,,
∴,
∴三个角中不满足“斜等边三角形”的定义,不符合题意;
当(1)②成立时,,,,,
∴,
∵,
∴是“斜等边三角形”,符合题意;
同理得:符合题意的只有,
故答案为:
三.解答题
17.解:(1)设这个多边形的边数是,
由题意得:,
,
∴这个多边形是八边形;
(2)设这个多边形的边数是,
由题意得:,
解得:,
为整数
,
∴重复加的那个角的度数是:
答:这个多边形的边数是,重复加的那个角的度数是.
18.解:AB+BC+AC>2BD.理由如下:
在△ABD中,AB+AD>BD,
在△BCD中,BC+CD>BD,
∴AB+AD+BC+CD>2BD,
即AB+BC+AC>2BD.
19.(1)如图所示,即为所求;
(2)如图所示,即为所求;
(3)如图所示,
∵平移后得到的
∴若连接,,
∴这两条线段之间的关系是平行且相等;
(4)如图所示,
的面积.
20.(1)解:∵,是边上的高,
∴,
∴,即的长度为;
(2)∵为边上的中线,
∴,
∴的周长的周长
,
即和的周长的差是2.
21.(1)解:在中,,,
∴,
∵是的角平分线.
∴,
∵线段是中 边上的高,
∴,
∴,
∴,
(2)解:∵,线段是中边上的高,
∴,
∵,
∴,
∵是的角平分线,
∴,
∴,
故答案为:;
(3)解:连接,
∵,,
∴,
∵由折叠所得,
∴,
∴.
22.(1)解:∵,,
∴,
∵,
∴,
∵,
∴;
(2),
证明:在中
∵,
∴,
在中,
∵,
∴,
∴,
∵,
∴;
(3)解:∵,,,
∴,
∴.
23.(1)解:如图所示,
∵
∴,
(2)证明:∵
∴,设
∵被平分
∴,则,
∴,
∵
∴,
∵平分
∴
∴,即的大小保持不变;
(3)解:在移动过程中,的大小保持不变;
如图所示,
证明:∵
∴,设
∵被平分
∴,则,
∴,
∵
∴,
∵平分
∴
∴,
∴,即的大小保持不变;
一.选择题(共10小题,满分30分,每小题3分)
1.下列实际情景运用了三角形稳定性的是( )
A.人能直立在地面上 B.校门口的自动伸缩栅栏门
C.古建筑中的三角形屋架 D.三轮车能在地面上运动而不会倒
2.如图,的三边长均为整数,且周长为,是边上的中线,的周长比的周长大2,则长的可能值有( )个.
A. B.
C. D.
3.下列命题是假命题的是( )
A.如果,,那么
B.对顶角相等
C.如果一个数能被整除,那么它肯定也能被整除
D.内错角相等
4.如图所示,∠F=90°,CE⊥AB,C是BF的中点,D是BE上的一点,下列说法正确的是( )
A.CD是△ABC的中线 B.AF是△ABC的高
C.CE是△ABF的中位线 D.AC是△ABF的角平分线
5.如图,在中,是的角平分线,,若,,则的度数为( )
A. B. C. D.
6.如图,在中,是边上任意一点,、、分别是、、的中点,,则的值为( )
A.2 B.4 C.6 D.8
7.如图,用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为3、4、5、7,且相邻两木条的夹角均可调整.若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值是( )
A.7 B.8 C.9 D.10
8.如图,中,,E分别在边,上,,,的平分线与的平分线交于点F,则的度数是( )
A.54° B.60° C.66° D.72°
9.如图,在中,平分,于点.的角平分线所在直线与射线相交于点,若,且,则的度数为( )
A. B. C. D.
10.如图,,、、分别平分,外角,外角,以下结论:①,②,③,④,其中正确的结论有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分,每小题3分)
11.如图,有一张三角形纸片,,,点是边上的固定点,在上找一点,将纸片沿折叠(为折痕),点落在点处,当与边平行时,的度数为 .
12.如图,为的中线,分别为,的一条高,若,则 .
13.已知的边长a,b,c满足,则a、b的值分别是 ,若c为偶数,则的周长为 .
14.如图,在中,点是边上一点,,连接,点是线段上一点,,连接,点是线段的中点,连接交线段于点,若的面积是12,则的面积是 .
15.如图和中,,,,点D在边上,将绕点O按每秒的速度沿顺时针方向旋转一周,在旋转的过程中当时,旋转时间 秒.
16.如果三角形中任意两个内角与满足,那么我们称这样的三角形为“斜等边三角形”.在锐角三角形中,于点D,若、、都是“斜等边三角形”,则 .
三.解答题(共7小题,满分52分)
17.(6分)(1)一个多边形的内角和是外角和的3倍,这个多边形是几边形?
(2)小明求得一个多边形的内角和为,小强很快发现小明所得的度数有误,后来小明复查时发现他重复加了一个内角,求出这个多边形的边数以及他重复加的那个角的度数.
18.(6分)如图所示,D是△ABC的边AC上任意一点(不含端点),连结BD,请判断AB+BC+AC与2BD的大小关系,并说明理由.
19.(8分)在正方形网格中,每个小正方形的边长均为1个单位长度,的三个顶点的位置如图所示.将平移,使点C平移至点D,点A、B的对应点分别是点E、F.
(1)在图中请画出平移后得到的;
(2)在图中画出的边上的高;
(3)若连接,则这两条线段之间的关系是 ;
(4)的面积为 .
20.(8分)如图所示,已知,分别是的高和中线,,,,.
(1)求的长;
(2)求和周长的差.
21.(8分)在中,,均为锐角且不相等,线段是中边上的高,是的角平分线.
(1)如图1,,,求的度数;
(2)若,,则______;
(3)是射线上一动点,C、H分别为线段A,上的点(不与端点重合),将沿着折叠,使点B落到点F处,如图2所示,请直接写出,与的数量关系.
22.(8分)已知,在中,,点在上,过点的一条直线与直线、分别交于点、.
(1)如图1,,则______°.
(2)如图2,猜想、、之间的数量关系,并加以证明;
(3)如图3,直接写出、、之间的数量关系______.
23.(8分)将含角的三角板()和含角的三角板及一把直尺按图方式摆放在起.使两块三角板的直角顶点,重合.点,,,始终落在直尺的边所在直线上.将含角的三角板沿直线向右平移.
(1)当点与点重合,请在备用图中补全图形,并求平移后与形成的夹角的度数;
(2)如图,点在线段上移动,是边上的动点,满足被平分,的平分线与边交于点,请证明在移动过程中,的大小保持不变;
(3)仿照(2)的探究,点在射线上移动,是边上的动点,满足被平分,的平分线所在直线与直线交于点,请写出一个与平移过程有关的合理猜想.(不用证明)
答案
一.选择题
1.C
【分析】根据三角形的稳定性进行判断即可求解.
【详解】解:古建筑中的三角形屋架是利用了三角形的稳定性,
故选C
2.B
【分析】依据的周长为22,的周长比的周长大2,可得,再根据的三边长均为整数,即可得到,6,8,10.
【详解】解:的周长为22,的周长比的周长大2,
,
解得,
又的三边长均为整数,的周长比的周长大2,
为整数,
边长为偶数,
,6,8,10,
即的长可能值有4个,
故选:B.
3.D
【分析】利用对顶角的性质、实数的性质、平行线的性质分别判断后即可确定正确的选项.
【详解】解:、如果,,那么,正确,是真命题,故本选项不符合题意;
、对顶角相等,正确,是真命题,故本选项不符合题意;
、如果一个数能被整除,那么它肯定也能被整除,正确,是真命题,故本选项不符合题意;
、两直线平行,内错角相等,原命题是假命题,故本选项符合题意.
故选:.
4.B
【分析】根据三角形中位线的定义,三角形角平分线、中线和高的定义作答.
【详解】解:A、AC是△ABC的中线,故本选项不符合题意.
B、由∠F=90°知,AF是△ABC的高,故本选项符合题意.
C、CE是△ABC的高,故本选项不符合题意.
D、AC是△ABF的中线,故本选项不符合题意.
故选:B.
5.C
【分析】根据三角形内角和定理求出,再根据角平分线的定义可得,最后利用垂线的定义可得,进而解答即可.
【详解】解:∵,
∴.
∵平分,
∴.
∵,
∴,
∴.
故选C.
6.C
【分析】根据三角形的中线把三角形分成两个面积相等的三角形解答.
【详解】解:连接,如图所示:
∵点D是的中点,
∴,
∴,
∴,
∵点E是的中点,
∴,
∵点F是的中点,
∴.
故选:C.
7.C
【分析】若两螺丝的距离最大,则此时这个木框的形状为三角形,根据三角形任意两边之和大于第三边,进行求解即可.
【详解】解:①当、在一条直线上时,三边长为:、、,
此时最大距离为;
②,
、不可能在一条直线上;
③当、在一条直线上时,三边长为:、、,
此时最大距离为;
④,
、不可能在一条直线上;
综上所述:最大距离为.
故选:C.
8.B
【分析】根据题意可知,设,表示出,根据角平分线的定义,可得的度数,根据列方程,即可求出的度数.
【详解】解:∵平分,
∴,
∵,
∴,
设,则,
∵,
∴,
∵,
∴,
∵平分,
∴,
∵,
∴,
∴.
故选:B.
9.C
【分析】由角平分线的定义可以得到,,设,假设,,通过角的等量代换可得到,代入的值即可.
【详解】∵平分,平分
∴,
设
∵
∴可以假设,
∴
∵
∴
∴
设,则
∴
∴
∵
∴
故答案选:C
10.D
【分析】根据角平分线的定义、三角形的内角和定理、三角形的外角性质、平行线的判定一一判定即可.
【详解】解:①设点A、B在直线上,
∵、分别平分的内角,外角,
∴平分的外角,
∴,
∵,且,
∴,
∴,故①正确.
②∵、分别平分的内角、外角,
∴,
∴,故②正确.
③∵,,
∴,
∴,
∵,
∴,
∴,故③正确.
④∵
∴,
∴,故④正确.
故选:D.
二.填空题
11.
【分析】根据已知、折叠和平行线,得,再计算的度数,最后根据三角形内角和为计算的度数即可.
【详解】,,,
(两直线平行,同位角相等),
纸片沿折叠(为折痕),点落在点处,
,
(三角形内角和为),
故答案为:.
12.9
【分析】由为的中线得,从而得到,代入进行计算即可得到答案.
【详解】解: 为的中线,
,
,
分别为,的一条高,
,
,
,
故答案为:9.
13. 2、4 10
【分析】由,可得,,解得,,由三角形三边关系可得,,即,由c为偶数,可得,然后求周长即可.
【详解】解:∵,
∴,,
解得,,
由三角形三边关系可得,,即,
∵c为偶数,
∴,
∴的周长为,
故答案为:2、4,10.
14.
【分析】连接,.由题意中的线段的比和,可推出,,从而可求出,.结合中点的性质即得出,从而可求出,进而得出,最后即得出,最后即可求出.
【详解】解:如图,连接,.
∵,,
∴,.
又∵,
∴,.
∵点是线段的中点,
∴.
∵,
∴,
∴,
∴,
∴,即,
∴,
∴.
故答案为:.
15.11或29
【分析】根据题意,画出图形,进行分类讨论,①当点C在内时,根据三角形的内角和定理可得,根据平行线的性质得出,再根据三角形的外角定理求出,进而得出,即可求解;②当点C在外时,延长交于一点,根据平行线的性质得出,再根据三角形的外角定理求出 ,即可得出,即可求解.
【详解】解:①当点C在内时,如图,
在中,,
∴,
∵,,
∴,
∵,
∴,
∴,
∴旋转时间(秒),
②当点C在外时,延长交于一点,如图,
∵,,
∴,
由①可得,,
∴,
∴,
∴绕点O沿顺时针方向旋转了,
∴旋转时间(秒),
故答案为:11或29.
16.
【分析】根据新定义的“斜等边三角形”的特点分情况分析,然后利用三角形内角和定理求解即可.
【详解】解:是“斜等边三角形”, ,
∴
(1),
∵,
∴解得:,;
(2),
∴解得:,;
(3),
∵,
∴解得:,;
(4),
∴解得:,;
是“斜等边三角形”,
①,
∵,
∴解得:,;
②,
∴解得:,;
③,
∵,
∴解得:,;
④,
∴解得:,;
当(1)①成立时,,,,,
∴,
∴三个角中不满足“斜等边三角形”的定义,不符合题意;
当(1)②成立时,,,,,
∴,
∵,
∴是“斜等边三角形”,符合题意;
同理得:符合题意的只有,
故答案为:
三.解答题
17.解:(1)设这个多边形的边数是,
由题意得:,
,
∴这个多边形是八边形;
(2)设这个多边形的边数是,
由题意得:,
解得:,
为整数
,
∴重复加的那个角的度数是:
答:这个多边形的边数是,重复加的那个角的度数是.
18.解:AB+BC+AC>2BD.理由如下:
在△ABD中,AB+AD>BD,
在△BCD中,BC+CD>BD,
∴AB+AD+BC+CD>2BD,
即AB+BC+AC>2BD.
19.(1)如图所示,即为所求;
(2)如图所示,即为所求;
(3)如图所示,
∵平移后得到的
∴若连接,,
∴这两条线段之间的关系是平行且相等;
(4)如图所示,
的面积.
20.(1)解:∵,是边上的高,
∴,
∴,即的长度为;
(2)∵为边上的中线,
∴,
∴的周长的周长
,
即和的周长的差是2.
21.(1)解:在中,,,
∴,
∵是的角平分线.
∴,
∵线段是中 边上的高,
∴,
∴,
∴,
(2)解:∵,线段是中边上的高,
∴,
∵,
∴,
∵是的角平分线,
∴,
∴,
故答案为:;
(3)解:连接,
∵,,
∴,
∵由折叠所得,
∴,
∴.
22.(1)解:∵,,
∴,
∵,
∴,
∵,
∴;
(2),
证明:在中
∵,
∴,
在中,
∵,
∴,
∴,
∵,
∴;
(3)解:∵,,,
∴,
∴.
23.(1)解:如图所示,
∵
∴,
(2)证明:∵
∴,设
∵被平分
∴,则,
∴,
∵
∴,
∵平分
∴
∴,即的大小保持不变;
(3)解:在移动过程中,的大小保持不变;
如图所示,
证明:∵
∴,设
∵被平分
∴,则,
∴,
∵
∴,
∵平分
∴
∴,
∴,即的大小保持不变;
