六年级下册数学冀教版第六单元 数的认识 质数合数因数倍数(课件)(共26张PPT)
文档属性
| 名称 | 六年级下册数学冀教版第六单元 数的认识 质数合数因数倍数(课件)(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 408.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 00:00:00 | ||
图片预览







文档简介
(共26张PPT)
质数合数因数倍数
数的认识
因数和倍数 自然数(0除外)
意义:如果a÷b=c(a、b、c均为非0自然数),那么a是b和c的倍数,
b和c是a的因数。
因数和倍数是相互依存的关系
1. 一个数的最大因数和最小倍数都是它本身
2. 1是所有非0自然数的因数,任何自然数都是1的倍数。
因数和倍数
1.填一填。
(1)18的因数有( );50以内8的倍数有( )。
(2)一个数的最大因数和最小倍数都是15,这个数是( )。
特点:一个数的因数的个数是有限的,其中最小的因数是1,最大的
因数是它本身。
一个数的倍数的个数是无限的,其中最小的倍数是它本身。
1,2,3,6,9,18
15
8,16,24,32,40,48
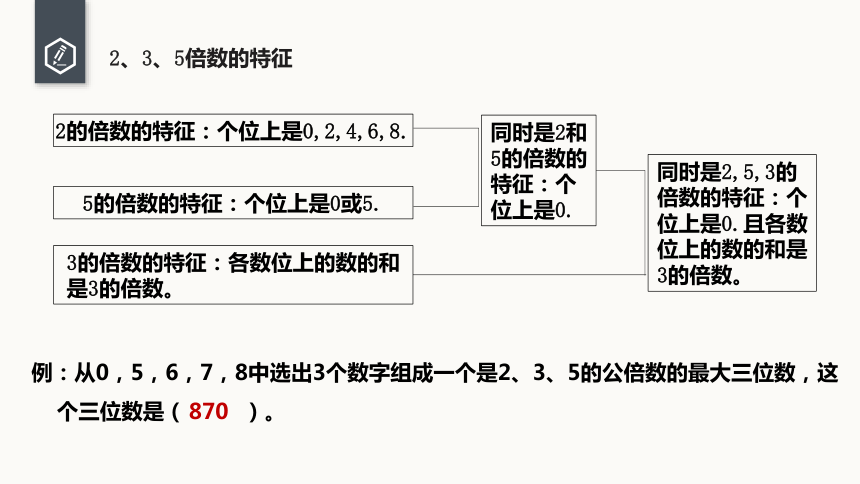
2、3、5倍数的特征
3的倍数的特征:各数位上的数的和是3的倍数。
2的倍数的特征:个位上是0,2,4,6,8.
5的倍数的特征:个位上是0或5.
同时是2和5的倍数的特征:个位上是0.
同时是2,5,3的倍数的特征:个位上是0.且各数位上的数的和是3的倍数。
例:从0,5,6,7,8中选出3个数字组成一个是2、3、5的公倍数的最大三位数,这个三位数是( )。
870
奇数与偶数 自然数
奇数:不是2的倍数的数都是奇数。也叫单数。
偶数:2的倍数都是偶数。也叫双数。
偶数±偶数=偶数 奇数±奇数=偶数 奇数±偶数=奇数
偶数×偶数=偶数 偶数×奇数=偶数 奇数×奇数=奇数
一个自然数不是奇数就是偶数;
相邻的两个奇数(或偶数)相差2;
最小的偶数是0,最小的奇数是1;
奇数与偶数
例:7个连续偶数的平均数是78,其中最小的偶数是多少?
78-6=72
例:已知a,b,c三个数中,有一个是5,有一个数6,有一个是7,那么(a-1)(b-2)(c-3)的结果是( )。
A. 奇数 B. 偶数 C. 奇数、偶数都有可能
B
在连乘的式子中,有一个因数是偶数,其结果必为偶数。
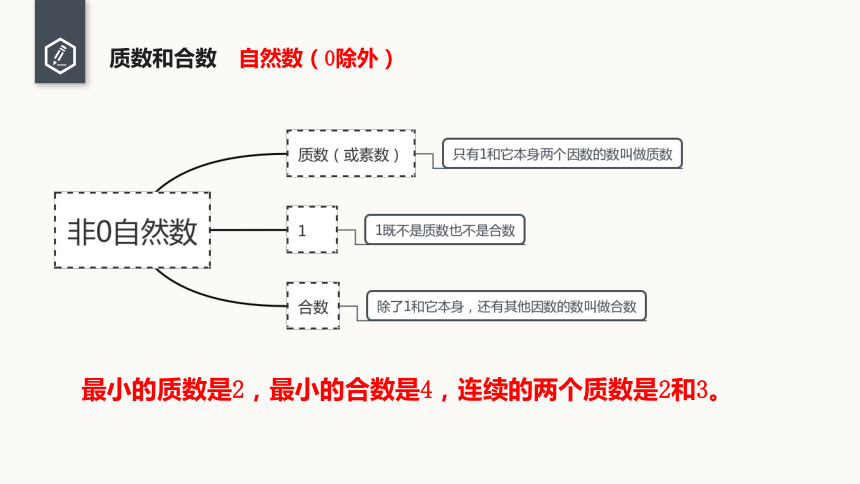
质数和合数 自然数(0除外)
最小的质数是2,最小的合数是4,连续的两个质数是2和3。
质因数和分解质因数
意义:任何一个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数,也叫这个合数的质因数。
如15=3×5,3和5都是15的因数,也是15的质因数。
把一个数用质数相乘的形式表现出来,叫做分解质因数。
30
2
15
3
5
30=2×3×5
把30分解质因数正确的做法是( )。
A.30=1×2×3×5
B.2×3×5=30
C.30=2×3×5
C
把30分解质因数
1不是质数
书写格式不符
公因数和最大公因数,公倍数和最小公倍数
公因数:
几个数公有的因数,叫做这几个数的公因数。
例:( )是8和12的公因数,( )是8和12的最大公因数。
1,2,4
4
公倍数:
几个数公有的倍数,叫做这几个数的公倍数。
例:( )都是4和6的公倍数,( )是4和6的最小公倍数。
12,24,36…
12
互质数:
公因数只有1的两个数叫做互质数。
⑴ 两个不同的质数一定互质。 ⑵ 相邻的两个非零自然数互质。
⑶ 1和任何非零自然数都互质。 ⑷ 2和任何奇数都互质。
互质数的几种特殊情况:
最大公因数:
公因数中其中最大的一个叫做这几个数的最大公因数。
最小公倍数:
其中最小的一个叫做这几个数的最小公倍数。
1.用a表示一个大于1的自然数,则a2一定是( )。
A. 质数 B. 合数 C. 不能确定
B
2.有4个小朋友,恰好一个比一个大1岁,将他们的年龄数相乘,积是5040。求这4个小朋友的年龄。
5040 = 2 X 2 X 2 X 2X 3 X 3 X 5X 7
=7 X 8 X 9 X 10
答:这4个小朋友的年龄分别是7岁、8岁、9岁、10岁。
求解两个数最大公因数和最小公倍数倍数的方法
列举法:先写出这两个数的所有因数,再找出这两个数的公因数,从公因数中找出最大公因数。
8的因数: 1,2,4,8.
12的因数:1,2,3,4,6,12.
筛选法:先找出较小数的所有因数,再从中圈出较大的因数,并从中找到较大的一个。
8的因数: 1 ,2 ,4 ,8.
在8的因数中,1,2,4也是12的因数。8和12的最大公因数是4.
8和12的最大公因数是4.
求解两个数最大公因数和最小公倍数的方法
分解质因数法:先将这两个数分别分解质因数,再从分解的质因数中找出这两个数公有的质因数,所有公因数的质因数相乘的积就是这两个公因数的最大公因数。
8= 2 X 2 X 2
12= 2 X 2 X 3
短除法:用两个数公有的质因数同时去除这两个数,除到所有的商只有公因数1,再将所有的除数相乘。
8和12的最大公因数是4.
8 12
2
4
6
2
2
3
8和12的最大公因数是 2 X 2=4.
求解两个数最大公因数和最小公倍数的方法
列举法:先写出这两个数各自的倍数,再从中找到它们的公倍数和最小公倍数。
8的倍数:8,16,24,32.....
12的倍数: 12,24,36,48.....
筛选法:先写出两个数中较大数(或较小数)的倍数,然后从较大数(或较小数)的倍数中按从小到大的顺序圈出较小数(或较大数)的倍数,第一个圈出的数就是这两个数的最小公倍数。
8的倍数:8,16,24,32,40,48.....
8的倍数中是12的倍数的数有:24,48...
8和12的最小公倍数是24.
8和12的最小公倍数是24.
求解两个数最大公因数和最小公倍数的方法
短除法:用两个数公有的质因数去除这两个数,直到所有的商只有公因数1,再将所有的除数和最后的商相乘,就可求出这两个数的最小公倍数。
8 12
2
4
6
2
2
3
8和12的最小公倍数是24。
6
的因数
24的因数
6和24的公因数
6和24的最大公因数是__________。
因为2×3=6,所以2和3是6的因数。
因为1×6=6,所以1和6是6的因数。
1
因为1×24=24,所以1和24是24的因数。
因为2×12=24,所以2和12是24的因数。
因为3×8=24,所以3和8是24的因数。
因为4×6=24,所以4和6是24的因数。
6的因数是1、2、3、6
24的因数是1、2、3、4、6、8、12、24
2
3
6
4、
8
12、
24
6
1.在图里填上合适的数。
(1)
4
的倍数
6的倍数
4和6的公倍数
4和6的最小公倍数是__________。
(2) 30以内的自然数中
30以内4的倍数是:4、8、12、16、20、24、28。
30以内6的倍数是:6、12、18、24、30 。
12
24
4
8、
16
20、
28
6
18
30
12
2.在图里填上合适的数。
3.求24和36的最大公因数和最小公倍数。
24 36
2
12
18
2
6
9
3
2
3
24和36的最大公因数是:2×2×3=12
24和36的最小公倍数是: 2×2×3×2×3=72
商互质
除数相乘
所有的除数和商相乘
短除法。
4.(1)a÷b=0.1(a、b都是非0自然数),那么a和b的最大公因数是( ),最小公倍数是( ).
(2)a÷b=1......1(a、b都是非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )
a
1
b
ab
5.已知A=2×3×m,B=3×5×m(m是自然数且m≠0),如果A和B的最大公因数是21,则m是( ),A和B的最小公倍数是( ).
7
210
求两个数的最大公因数和最小公倍数的特殊情况
(1)成倍数关系的两个数,较小数是他们的最大公因数,较大数是他们的最小公倍数。
(2)两个互质数的最小公倍数是它们的乘积。
1.a÷b=0.1(a、b都是非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
2.a÷b=1……1(a、b都是非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
a
b
1
ab
最大公因数和最小公倍数的应用
1.一间屋子的地面是一个长4.8m、宽4.2m米的长方形,如果全部用正方形地砖铺地(使用的地砖都是整块的),正方形地砖的边长最大是多少分米?铺满这间屋子的地面一共需要多少块这样的地砖?
因为48和42的最大公因数是6,所以正方形地砖的边长最大是6dm。
(48X42)÷(6X6)=2016÷36=56(块)
答:正方形地砖的边长最大6分米;铺满这间屋子的地面一共需要56块这样的地砖.
最大公因数和最小公倍数的应用
2.一箱苹果有40多个,如果把这箱苹果每8个装一盒,还剩余6个;如果把每10个装一盒,也剩余6个,这箱苹果有多少个?
因为8和10的最小公倍数是40,40+6=46(个),正好是40多个。
答:这箱苹果有46个。
巩固练习
02
PART
2.一个三位数,百位上既不是质数也不是合数,十位上是最大的一位奇数,个位上是2和3的倍数,这个三位数是( )。
196
1.一个九位数,最高位上的数字是最小的质数;千万位上的数字是最小的合数;千位上的数字既是2的倍数又是3的倍数;十位上的数字是最大的一位数;其余各位上的数字都是“0”,这个数写作( ),读作( ),改写成以“万”为单位的数是( ),四舍五入到亿位是( )。
240006090 二亿四千万六千零九十 24000.609万 2亿
3.连续5个自然数的和是60,最中间的自然数是( );连续5个奇数的和是65,其中最小的奇数是( )。
12
9
5.三个连续偶数的和是24,这三个数的最小公倍数是( )最大公因数是( )。
120
4.五(1)班分组进行实践活动,每组5人或每组7人都正好,五(1)班最少( )名学生,五(2)班学生每组10人或每组8人都剩3人,五(2)班最少有( )名学生。
35
6. 的分子加上4,要使分数的大小不变,分母应该加上( )。
14
43
2
8.李老师要把一块长36厘米,宽24厘米的纸板,裁成几个大小一样的正方形,正方形边长最大是多少厘米?可以裁多少个?
36=2×2×3×3 24=2×2×2×3
所以36和24的最大公因数是:2×2×3=12
(36÷12)×(24÷12)=3×2=6(个)
答:正方形的边长最大是12厘米,至少可以裁6个。
7.暑假期间,小玲每3天去图书馆看书一次,小芳每4天去一次。8月3日,她们在图书馆相遇,下次相遇是八月几日?
因为3和4的最小公倍数: 3×4= 12 也就是说再过12日就能在图书馆相遇。
根据这次都到图书馆的时间是8月3日,可推知她俩下一次在图书馆相遇的时间是8月15日。
谢谢观看
THANK .YOU
质数合数因数倍数
数的认识
因数和倍数 自然数(0除外)
意义:如果a÷b=c(a、b、c均为非0自然数),那么a是b和c的倍数,
b和c是a的因数。
因数和倍数是相互依存的关系
1. 一个数的最大因数和最小倍数都是它本身
2. 1是所有非0自然数的因数,任何自然数都是1的倍数。
因数和倍数
1.填一填。
(1)18的因数有( );50以内8的倍数有( )。
(2)一个数的最大因数和最小倍数都是15,这个数是( )。
特点:一个数的因数的个数是有限的,其中最小的因数是1,最大的
因数是它本身。
一个数的倍数的个数是无限的,其中最小的倍数是它本身。
1,2,3,6,9,18
15
8,16,24,32,40,48
2、3、5倍数的特征
3的倍数的特征:各数位上的数的和是3的倍数。
2的倍数的特征:个位上是0,2,4,6,8.
5的倍数的特征:个位上是0或5.
同时是2和5的倍数的特征:个位上是0.
同时是2,5,3的倍数的特征:个位上是0.且各数位上的数的和是3的倍数。
例:从0,5,6,7,8中选出3个数字组成一个是2、3、5的公倍数的最大三位数,这个三位数是( )。
870
奇数与偶数 自然数
奇数:不是2的倍数的数都是奇数。也叫单数。
偶数:2的倍数都是偶数。也叫双数。
偶数±偶数=偶数 奇数±奇数=偶数 奇数±偶数=奇数
偶数×偶数=偶数 偶数×奇数=偶数 奇数×奇数=奇数
一个自然数不是奇数就是偶数;
相邻的两个奇数(或偶数)相差2;
最小的偶数是0,最小的奇数是1;
奇数与偶数
例:7个连续偶数的平均数是78,其中最小的偶数是多少?
78-6=72
例:已知a,b,c三个数中,有一个是5,有一个数6,有一个是7,那么(a-1)(b-2)(c-3)的结果是( )。
A. 奇数 B. 偶数 C. 奇数、偶数都有可能
B
在连乘的式子中,有一个因数是偶数,其结果必为偶数。
质数和合数 自然数(0除外)
最小的质数是2,最小的合数是4,连续的两个质数是2和3。
质因数和分解质因数
意义:任何一个合数都可以写成几个质数相乘的形式,其中每个质数都是这个合数的因数,也叫这个合数的质因数。
如15=3×5,3和5都是15的因数,也是15的质因数。
把一个数用质数相乘的形式表现出来,叫做分解质因数。
30
2
15
3
5
30=2×3×5
把30分解质因数正确的做法是( )。
A.30=1×2×3×5
B.2×3×5=30
C.30=2×3×5
C
把30分解质因数
1不是质数
书写格式不符
公因数和最大公因数,公倍数和最小公倍数
公因数:
几个数公有的因数,叫做这几个数的公因数。
例:( )是8和12的公因数,( )是8和12的最大公因数。
1,2,4
4
公倍数:
几个数公有的倍数,叫做这几个数的公倍数。
例:( )都是4和6的公倍数,( )是4和6的最小公倍数。
12,24,36…
12
互质数:
公因数只有1的两个数叫做互质数。
⑴ 两个不同的质数一定互质。 ⑵ 相邻的两个非零自然数互质。
⑶ 1和任何非零自然数都互质。 ⑷ 2和任何奇数都互质。
互质数的几种特殊情况:
最大公因数:
公因数中其中最大的一个叫做这几个数的最大公因数。
最小公倍数:
其中最小的一个叫做这几个数的最小公倍数。
1.用a表示一个大于1的自然数,则a2一定是( )。
A. 质数 B. 合数 C. 不能确定
B
2.有4个小朋友,恰好一个比一个大1岁,将他们的年龄数相乘,积是5040。求这4个小朋友的年龄。
5040 = 2 X 2 X 2 X 2X 3 X 3 X 5X 7
=7 X 8 X 9 X 10
答:这4个小朋友的年龄分别是7岁、8岁、9岁、10岁。
求解两个数最大公因数和最小公倍数倍数的方法
列举法:先写出这两个数的所有因数,再找出这两个数的公因数,从公因数中找出最大公因数。
8的因数: 1,2,4,8.
12的因数:1,2,3,4,6,12.
筛选法:先找出较小数的所有因数,再从中圈出较大的因数,并从中找到较大的一个。
8的因数: 1 ,2 ,4 ,8.
在8的因数中,1,2,4也是12的因数。8和12的最大公因数是4.
8和12的最大公因数是4.
求解两个数最大公因数和最小公倍数的方法
分解质因数法:先将这两个数分别分解质因数,再从分解的质因数中找出这两个数公有的质因数,所有公因数的质因数相乘的积就是这两个公因数的最大公因数。
8= 2 X 2 X 2
12= 2 X 2 X 3
短除法:用两个数公有的质因数同时去除这两个数,除到所有的商只有公因数1,再将所有的除数相乘。
8和12的最大公因数是4.
8 12
2
4
6
2
2
3
8和12的最大公因数是 2 X 2=4.
求解两个数最大公因数和最小公倍数的方法
列举法:先写出这两个数各自的倍数,再从中找到它们的公倍数和最小公倍数。
8的倍数:8,16,24,32.....
12的倍数: 12,24,36,48.....
筛选法:先写出两个数中较大数(或较小数)的倍数,然后从较大数(或较小数)的倍数中按从小到大的顺序圈出较小数(或较大数)的倍数,第一个圈出的数就是这两个数的最小公倍数。
8的倍数:8,16,24,32,40,48.....
8的倍数中是12的倍数的数有:24,48...
8和12的最小公倍数是24.
8和12的最小公倍数是24.
求解两个数最大公因数和最小公倍数的方法
短除法:用两个数公有的质因数去除这两个数,直到所有的商只有公因数1,再将所有的除数和最后的商相乘,就可求出这两个数的最小公倍数。
8 12
2
4
6
2
2
3
8和12的最小公倍数是24。
6
的因数
24的因数
6和24的公因数
6和24的最大公因数是__________。
因为2×3=6,所以2和3是6的因数。
因为1×6=6,所以1和6是6的因数。
1
因为1×24=24,所以1和24是24的因数。
因为2×12=24,所以2和12是24的因数。
因为3×8=24,所以3和8是24的因数。
因为4×6=24,所以4和6是24的因数。
6的因数是1、2、3、6
24的因数是1、2、3、4、6、8、12、24
2
3
6
4、
8
12、
24
6
1.在图里填上合适的数。
(1)
4
的倍数
6的倍数
4和6的公倍数
4和6的最小公倍数是__________。
(2) 30以内的自然数中
30以内4的倍数是:4、8、12、16、20、24、28。
30以内6的倍数是:6、12、18、24、30 。
12
24
4
8、
16
20、
28
6
18
30
12
2.在图里填上合适的数。
3.求24和36的最大公因数和最小公倍数。
24 36
2
12
18
2
6
9
3
2
3
24和36的最大公因数是:2×2×3=12
24和36的最小公倍数是: 2×2×3×2×3=72
商互质
除数相乘
所有的除数和商相乘
短除法。
4.(1)a÷b=0.1(a、b都是非0自然数),那么a和b的最大公因数是( ),最小公倍数是( ).
(2)a÷b=1......1(a、b都是非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )
a
1
b
ab
5.已知A=2×3×m,B=3×5×m(m是自然数且m≠0),如果A和B的最大公因数是21,则m是( ),A和B的最小公倍数是( ).
7
210
求两个数的最大公因数和最小公倍数的特殊情况
(1)成倍数关系的两个数,较小数是他们的最大公因数,较大数是他们的最小公倍数。
(2)两个互质数的最小公倍数是它们的乘积。
1.a÷b=0.1(a、b都是非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
2.a÷b=1……1(a、b都是非0自然数),那么a和b的最大公因数是( ),最小公倍数是( )。
a
b
1
ab
最大公因数和最小公倍数的应用
1.一间屋子的地面是一个长4.8m、宽4.2m米的长方形,如果全部用正方形地砖铺地(使用的地砖都是整块的),正方形地砖的边长最大是多少分米?铺满这间屋子的地面一共需要多少块这样的地砖?
因为48和42的最大公因数是6,所以正方形地砖的边长最大是6dm。
(48X42)÷(6X6)=2016÷36=56(块)
答:正方形地砖的边长最大6分米;铺满这间屋子的地面一共需要56块这样的地砖.
最大公因数和最小公倍数的应用
2.一箱苹果有40多个,如果把这箱苹果每8个装一盒,还剩余6个;如果把每10个装一盒,也剩余6个,这箱苹果有多少个?
因为8和10的最小公倍数是40,40+6=46(个),正好是40多个。
答:这箱苹果有46个。
巩固练习
02
PART
2.一个三位数,百位上既不是质数也不是合数,十位上是最大的一位奇数,个位上是2和3的倍数,这个三位数是( )。
196
1.一个九位数,最高位上的数字是最小的质数;千万位上的数字是最小的合数;千位上的数字既是2的倍数又是3的倍数;十位上的数字是最大的一位数;其余各位上的数字都是“0”,这个数写作( ),读作( ),改写成以“万”为单位的数是( ),四舍五入到亿位是( )。
240006090 二亿四千万六千零九十 24000.609万 2亿
3.连续5个自然数的和是60,最中间的自然数是( );连续5个奇数的和是65,其中最小的奇数是( )。
12
9
5.三个连续偶数的和是24,这三个数的最小公倍数是( )最大公因数是( )。
120
4.五(1)班分组进行实践活动,每组5人或每组7人都正好,五(1)班最少( )名学生,五(2)班学生每组10人或每组8人都剩3人,五(2)班最少有( )名学生。
35
6. 的分子加上4,要使分数的大小不变,分母应该加上( )。
14
43
2
8.李老师要把一块长36厘米,宽24厘米的纸板,裁成几个大小一样的正方形,正方形边长最大是多少厘米?可以裁多少个?
36=2×2×3×3 24=2×2×2×3
所以36和24的最大公因数是:2×2×3=12
(36÷12)×(24÷12)=3×2=6(个)
答:正方形的边长最大是12厘米,至少可以裁6个。
7.暑假期间,小玲每3天去图书馆看书一次,小芳每4天去一次。8月3日,她们在图书馆相遇,下次相遇是八月几日?
因为3和4的最小公倍数: 3×4= 12 也就是说再过12日就能在图书馆相遇。
根据这次都到图书馆的时间是8月3日,可推知她俩下一次在图书馆相遇的时间是8月15日。
谢谢观看
THANK .YOU
