2024年内蒙古包头市中考数学模拟试卷(四)(无答案)
文档属性
| 名称 | 2024年内蒙古包头市中考数学模拟试卷(四)(无答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 112.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 00:00:00 | ||
图片预览

文档简介
2024年包头中考模拟四
一.选择题(共10小题,满分30分,每小题3分)
1. (3分)据不完全统计,2021年河北省中考报名人数已经超过了886000人,数据886000用科学记数法可以表示为( )
A.8.86×10 5 B.8.86×10 6 C.88.6×10 5 D.88.6×10 6
2. (3分)下列说法正确的是( )
A. 是 的算术平方根 B.-2是4的算术平方根
C.(-1) 2 的算术平方根是1 D.-9的算术平方根是3
3. (3分)下列计算中正确的有( )个.
①a 6 ÷a 2 =a 3 ;②(a 3 ) 2 =a 5 ;③a 3 +a 3 =a 6 ;④2 -1 =-2;⑤(π-3) 0 =1;⑥3 2 =6.
A.1 B.2 C.3 D.4
4. (3分)如图,由若干个小正方体组成的一个几何体,从它的正面看得到的平面图形是( )
A. B. C. D.
5. (3分)如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
A.50° B.40° C.30° D.20°
6. (3分)二维码的图案主要由黑、白两种小正方形组成.现对由4个小正方形组成的“田”进行涂色,每个小正方形随机涂成黑色或白色,则恰好涂成两个黑色和两个白色的概率为( )
A. B. C. D.
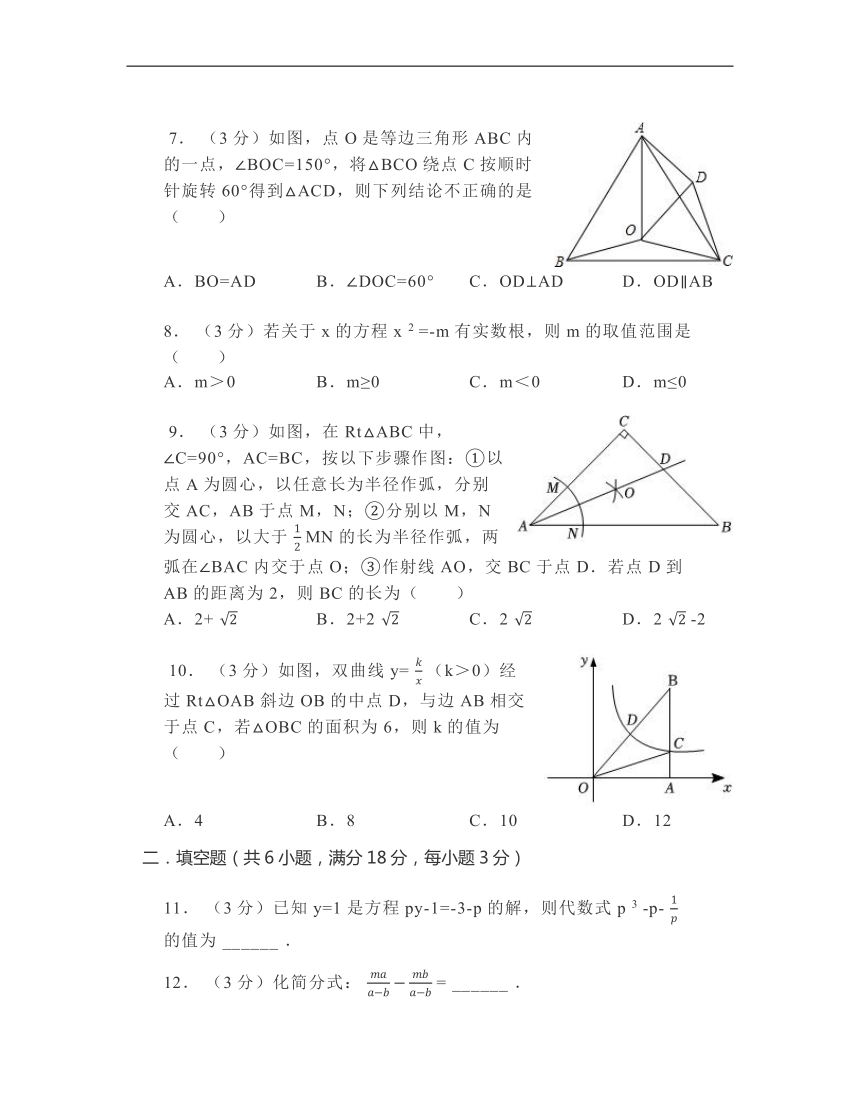
7. (3分)如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BCO绕点C按顺时针旋转60°得到△ACD,则下列结论不正确的是( )
A.BO=AD B.∠DOC=60° C.OD⊥AD D.OD∥AB
8. (3分)若关于x的方程x 2 =-m有实数根,则m的取值范围是( )
A.m>0 B.m≥0 C.m<0 D.m≤0
9. (3分)如图,在Rt△ABC中,∠C=90°,AC=BC,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AC,AB于点M,N;②分别以M,N为圆心,以大于 MN的长为半径作弧,两弧在∠BAC内交于点O;③作射线AO,交BC于点D.若点D到AB的距离为2,则BC的长为( )
A.2+ B.2+2 C.2 D.2 -2
10. (3分)如图,双曲线y= (k>0)经过Rt△OAB斜边OB的中点D,与边AB相交于点C,若△OBC的面积为6,则k的值为( )
A.4 B.8 C.10 D.12
二.填空题(共6小题,满分18分,每小题3分)
11. (3分)已知y=1是方程py-1=-3-p的解,则代数式p 3 -p- 的值为 ______ .
12. (3分)化简分式: = ______ .
13. (3分)如图,平面直角坐标系中,A、B的坐标分别为(2,0)、(0,1),若将线段AB平移至A 1 B 1 ,则a+b的值为 ______ .
14. (3分)若点P(a,b)在抛物线y=-x 2 +2x-1,则a+b的最大值为 ______ .
15. (3分)如图所示,扇形AOB的圆心角是直角,半径为 ,C为OA边上一点,将△BOC沿BC边折叠,圆心O恰好落在弧AB上的点D处,则阴影部分的面积为 ______ .
16. (3分)如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
(1)图中△APD与哪个三角形全等: ______ .
(2)猜想:线段PC、PE、PF之间存在什么关系: ______ .
三.解答题(共7小题,满分72分)
17. (8分)(1)解不等式:
(2)化简求值:2(x-1)(x+3)-(x+2) 2 ,其中 .
18. (8分)实施乡村振兴战略,能够将发展机遇提供给农业生产,改善乡村面貌提高农民的生活质量,促进机械化发展以及农业现代化发展.为助力乡村产业振兴,某地利用网络销售农产品,一段时间后负责人随机抽取部分销售人员统计他们上一个月的销售额m(单位:万元),绘制成如下统计图表(尚不完整):
等级 销方元 人数(频数) 各组平均值
A 0≤m<5 4 3.5
B 5≤m<10 8 7.5
C 10≤m<15 m 12
D 15≤m<20 2 17
其中B等级销售人员的销售额分别是(万元):5,6,7,8,8,8,9,9.请根据图表中的信息,解答下列问题:
(1)填空:m= ______ ,B等级销售人员的销售额的众数是 ______ ,所抽取销售人员的销售额的中位数是 ______ ;
(2)若想让一半左右的销售人员都能达到销售目标,你认为月销售额目标定为多少合适?说明理由;
(3)若该地共有80位网络销售人员销售农产品,请估计该地上个月农产品的网络销售总额.
19. (8分)某校数学社团利用自制测角仪和皮尺测量河宽(把河两岸看作平行线).如图,他们在河岸MN一侧的A处,观察到对岸P点处有一棵树,测得∠PAN=31°,向前走45m到达B处,测得∠PBN=45°,求河的宽度(精确到1m).(sin31°≈0.52,cos31°≈0.86,tan31°≈0.60, ≈1.41)
20. (11分)为进一步加强“书香校园”建设,某学校拟购进甲、乙两种规格的书柜放置新购买的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用7200元购进的甲种书柜的数量比用7500元购进乙种书柜的数量少5个.
(1)每个甲种书柜的进价是多少元?
(2)若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的2倍.该校应如何进货使得购进书柜所需费用最少?
21. (12分)如图,在Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,连接OA、OA=OB.
(1)求证:∠ABC=30°;
(2)连接AD,若 ,求⊙O的半径.
22. (12分)操作:如图①在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD内部,延长AF交CD于点G.易知FG=GC.
探究:若将图①中的正方形改成矩形,其他条件不变,如图②,那么线段GF与GC相等吗?请说明理由.
拓展:如图③,将图①中的正方形ABCD改为平行四边形,其他条件不变,若AB=3,AD=4,则△AGD的周长为 ______ .
23. (13分)抛物线y=ax 2 +bx+2交x轴于A(1,0)、B(3,0)两点,交y轴于点C,点P为线段BC下方抛物线上一动点,连接BP,CP.
(1)求抛物线解析式;
(2)在点P移动过程中,△BPC的面积是否存在最大值?若存在,求出最大面积及点P的坐标,若不存在,请说明理由;
(3)设点D为CB上不与端点重合的一动点,过点D作线段BC的垂线,交抛物线于点E,若△DCE与△BOC相似,请直接写出点E的坐标.
一.选择题(共10小题,满分30分,每小题3分)
1. (3分)据不完全统计,2021年河北省中考报名人数已经超过了886000人,数据886000用科学记数法可以表示为( )
A.8.86×10 5 B.8.86×10 6 C.88.6×10 5 D.88.6×10 6
2. (3分)下列说法正确的是( )
A. 是 的算术平方根 B.-2是4的算术平方根
C.(-1) 2 的算术平方根是1 D.-9的算术平方根是3
3. (3分)下列计算中正确的有( )个.
①a 6 ÷a 2 =a 3 ;②(a 3 ) 2 =a 5 ;③a 3 +a 3 =a 6 ;④2 -1 =-2;⑤(π-3) 0 =1;⑥3 2 =6.
A.1 B.2 C.3 D.4
4. (3分)如图,由若干个小正方体组成的一个几何体,从它的正面看得到的平面图形是( )
A. B. C. D.
5. (3分)如图,将三角形纸板的直角顶点放在直尺的一边上,∠1=20°,∠2=40°,则∠3等于( )
A.50° B.40° C.30° D.20°
6. (3分)二维码的图案主要由黑、白两种小正方形组成.现对由4个小正方形组成的“田”进行涂色,每个小正方形随机涂成黑色或白色,则恰好涂成两个黑色和两个白色的概率为( )
A. B. C. D.
7. (3分)如图,点O是等边三角形ABC内的一点,∠BOC=150°,将△BCO绕点C按顺时针旋转60°得到△ACD,则下列结论不正确的是( )
A.BO=AD B.∠DOC=60° C.OD⊥AD D.OD∥AB
8. (3分)若关于x的方程x 2 =-m有实数根,则m的取值范围是( )
A.m>0 B.m≥0 C.m<0 D.m≤0
9. (3分)如图,在Rt△ABC中,∠C=90°,AC=BC,按以下步骤作图:①以点A为圆心,以任意长为半径作弧,分别交AC,AB于点M,N;②分别以M,N为圆心,以大于 MN的长为半径作弧,两弧在∠BAC内交于点O;③作射线AO,交BC于点D.若点D到AB的距离为2,则BC的长为( )
A.2+ B.2+2 C.2 D.2 -2
10. (3分)如图,双曲线y= (k>0)经过Rt△OAB斜边OB的中点D,与边AB相交于点C,若△OBC的面积为6,则k的值为( )
A.4 B.8 C.10 D.12
二.填空题(共6小题,满分18分,每小题3分)
11. (3分)已知y=1是方程py-1=-3-p的解,则代数式p 3 -p- 的值为 ______ .
12. (3分)化简分式: = ______ .
13. (3分)如图,平面直角坐标系中,A、B的坐标分别为(2,0)、(0,1),若将线段AB平移至A 1 B 1 ,则a+b的值为 ______ .
14. (3分)若点P(a,b)在抛物线y=-x 2 +2x-1,则a+b的最大值为 ______ .
15. (3分)如图所示,扇形AOB的圆心角是直角,半径为 ,C为OA边上一点,将△BOC沿BC边折叠,圆心O恰好落在弧AB上的点D处,则阴影部分的面积为 ______ .
16. (3分)如图,点P是菱形ABCD的对角线BD上一点,连接CP并延长,交AD于E,交BA的延长线于点F.
(1)图中△APD与哪个三角形全等: ______ .
(2)猜想:线段PC、PE、PF之间存在什么关系: ______ .
三.解答题(共7小题,满分72分)
17. (8分)(1)解不等式:
(2)化简求值:2(x-1)(x+3)-(x+2) 2 ,其中 .
18. (8分)实施乡村振兴战略,能够将发展机遇提供给农业生产,改善乡村面貌提高农民的生活质量,促进机械化发展以及农业现代化发展.为助力乡村产业振兴,某地利用网络销售农产品,一段时间后负责人随机抽取部分销售人员统计他们上一个月的销售额m(单位:万元),绘制成如下统计图表(尚不完整):
等级 销方元 人数(频数) 各组平均值
A 0≤m<5 4 3.5
B 5≤m<10 8 7.5
C 10≤m<15 m 12
D 15≤m<20 2 17
其中B等级销售人员的销售额分别是(万元):5,6,7,8,8,8,9,9.请根据图表中的信息,解答下列问题:
(1)填空:m= ______ ,B等级销售人员的销售额的众数是 ______ ,所抽取销售人员的销售额的中位数是 ______ ;
(2)若想让一半左右的销售人员都能达到销售目标,你认为月销售额目标定为多少合适?说明理由;
(3)若该地共有80位网络销售人员销售农产品,请估计该地上个月农产品的网络销售总额.
19. (8分)某校数学社团利用自制测角仪和皮尺测量河宽(把河两岸看作平行线).如图,他们在河岸MN一侧的A处,观察到对岸P点处有一棵树,测得∠PAN=31°,向前走45m到达B处,测得∠PBN=45°,求河的宽度(精确到1m).(sin31°≈0.52,cos31°≈0.86,tan31°≈0.60, ≈1.41)
20. (11分)为进一步加强“书香校园”建设,某学校拟购进甲、乙两种规格的书柜放置新购买的图书.已知每个甲种书柜的进价比每个乙种书柜的进价高20%,用7200元购进的甲种书柜的数量比用7500元购进乙种书柜的数量少5个.
(1)每个甲种书柜的进价是多少元?
(2)若该校拟购进这两种规格的书柜共60个,其中乙种书柜的数量不大于甲种书柜数量的2倍.该校应如何进货使得购进书柜所需费用最少?
21. (12分)如图,在Rt△ABC中,∠ACB=90°,点D在BC边上,以CD为直径的⊙O与直线AB相切于点E,连接OA、OA=OB.
(1)求证:∠ABC=30°;
(2)连接AD,若 ,求⊙O的半径.
22. (12分)操作:如图①在正方形ABCD中,点E是BC的中点,将△ABE沿AE折叠后得到△AFE,点F在正方形ABCD内部,延长AF交CD于点G.易知FG=GC.
探究:若将图①中的正方形改成矩形,其他条件不变,如图②,那么线段GF与GC相等吗?请说明理由.
拓展:如图③,将图①中的正方形ABCD改为平行四边形,其他条件不变,若AB=3,AD=4,则△AGD的周长为 ______ .
23. (13分)抛物线y=ax 2 +bx+2交x轴于A(1,0)、B(3,0)两点,交y轴于点C,点P为线段BC下方抛物线上一动点,连接BP,CP.
(1)求抛物线解析式;
(2)在点P移动过程中,△BPC的面积是否存在最大值?若存在,求出最大面积及点P的坐标,若不存在,请说明理由;
(3)设点D为CB上不与端点重合的一动点,过点D作线段BC的垂线,交抛物线于点E,若△DCE与△BOC相似,请直接写出点E的坐标.
同课章节目录
