苏教版五下第三单元探索规律 和与积的奇偶性 课件
文档属性
| 名称 | 苏教版五下第三单元探索规律 和与积的奇偶性 课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 10:44:11 | ||
图片预览






文档简介
(共16张PPT)
探索规律
和与积的奇偶性
(苏教版)五年级
下
你能说说奇数和偶数各有什么特点吗?
是2的倍数的数叫作偶数。
不是2的倍数的数叫作奇数。
复习导入
任意选两个不是 0 的自然数, 求出它们的和, 再看看和是奇数还是偶数。
探究新知
111
36
6
8
14
15
73
147
7
16
88
23
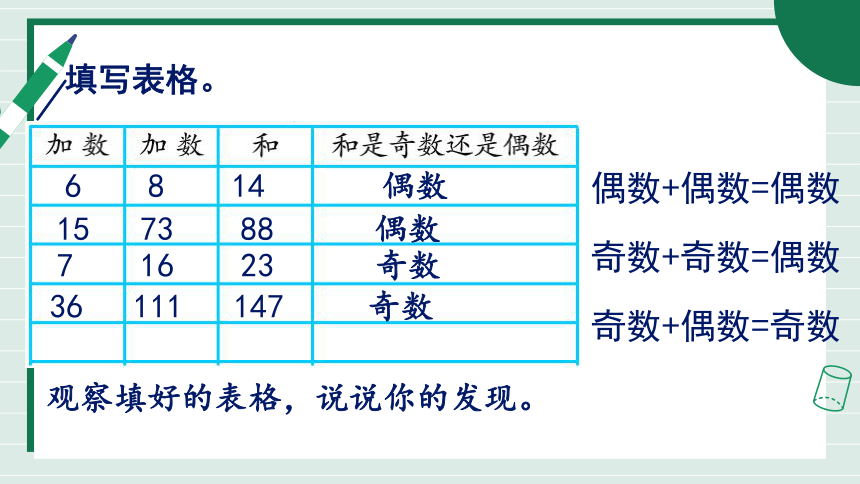
填写表格。
6 8 14 偶数
15 73 88 偶数
7 16 23 奇数
36 111 147 奇数
观察填好的表格,说说你的发现。
偶数+偶数=偶数
奇数+奇数=偶数
奇数+偶数=奇数
举例:任意选3个、4个、5个或5个以上不是0的自然数,写成两个连加算式,先算出和,再判断和是奇数还是偶数。
小组讨论:
1. 你写的连加算式中, 有几个加数是偶数?
有几个加数是奇数?
2. 和是奇数还是偶数,与加数中奇数的个数有
什么关系?
几个非0自然数连加,加数中,
奇数的个数是奇数,和是奇数;
奇数的个数是偶数,和是偶数。
几个数的乘积,什么情况下是奇数?什么情况下是偶数?
1 × 3 × 5 = 15
8 × 4 × 10 × 2 = 640
1 × 2 × 3 = 6
3 × 5 × 7 × 2 = 210
乘数都是奇数,
积也是奇数;
乘数都是偶数,
积也是偶数。
几个乘数中,
只要有一个偶数,
积一定是偶数。
回顾探索和发现规律的过程, 说说自己的体会。
多写一些算式,并进行比较,才能发现规律。
要注意从不同的算式中发现共同的特点。
举例和验证是发现规律的好方法。
摆 渡
1.小船最初停在南岸,从南岸驶向北岸,再从北岸驶向南岸,不断往返。请问小船摆渡11次后,船在南岸还是北岸?为什么?
北
南
对应练习
我来列表
摆渡次数 船所在的位置
1 北岸
2 南岸
3 北岸
南岸
… …
1 3 5
2 4
北岸
南岸
摆渡奇数次后,船在__岸;
摆渡偶数次后,船在__岸。
小船摆渡11次后,船在__岸。
北
南
北
2.不计算,直接判断下列算式的结果是
奇数还是偶数。
2.不计算,直接判断下列算式的结果是
奇数还是偶数。
偶数
通过这节课的学习活动,你有什么收获?
课堂小结
探索规律
和与积的奇偶性
(苏教版)五年级
下
你能说说奇数和偶数各有什么特点吗?
是2的倍数的数叫作偶数。
不是2的倍数的数叫作奇数。
复习导入
任意选两个不是 0 的自然数, 求出它们的和, 再看看和是奇数还是偶数。
探究新知
111
36
6
8
14
15
73
147
7
16
88
23
填写表格。
6 8 14 偶数
15 73 88 偶数
7 16 23 奇数
36 111 147 奇数
观察填好的表格,说说你的发现。
偶数+偶数=偶数
奇数+奇数=偶数
奇数+偶数=奇数
举例:任意选3个、4个、5个或5个以上不是0的自然数,写成两个连加算式,先算出和,再判断和是奇数还是偶数。
小组讨论:
1. 你写的连加算式中, 有几个加数是偶数?
有几个加数是奇数?
2. 和是奇数还是偶数,与加数中奇数的个数有
什么关系?
几个非0自然数连加,加数中,
奇数的个数是奇数,和是奇数;
奇数的个数是偶数,和是偶数。
几个数的乘积,什么情况下是奇数?什么情况下是偶数?
1 × 3 × 5 = 15
8 × 4 × 10 × 2 = 640
1 × 2 × 3 = 6
3 × 5 × 7 × 2 = 210
乘数都是奇数,
积也是奇数;
乘数都是偶数,
积也是偶数。
几个乘数中,
只要有一个偶数,
积一定是偶数。
回顾探索和发现规律的过程, 说说自己的体会。
多写一些算式,并进行比较,才能发现规律。
要注意从不同的算式中发现共同的特点。
举例和验证是发现规律的好方法。
摆 渡
1.小船最初停在南岸,从南岸驶向北岸,再从北岸驶向南岸,不断往返。请问小船摆渡11次后,船在南岸还是北岸?为什么?
北
南
对应练习
我来列表
摆渡次数 船所在的位置
1 北岸
2 南岸
3 北岸
南岸
… …
1 3 5
2 4
北岸
南岸
摆渡奇数次后,船在__岸;
摆渡偶数次后,船在__岸。
小船摆渡11次后,船在__岸。
北
南
北
2.不计算,直接判断下列算式的结果是
奇数还是偶数。
2.不计算,直接判断下列算式的结果是
奇数还是偶数。
偶数
通过这节课的学习活动,你有什么收获?
课堂小结
