沪科版八年级数学上册试题 期中测试卷 (含解析)
文档属性
| 名称 | 沪科版八年级数学上册试题 期中测试卷 (含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 633.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 00:00:00 | ||
图片预览



文档简介
期中测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.如图,直线与x轴交于点,下列说法正确的是( )
A.
B.直线经过第三象限
C.关于x的方程的解为
D.若,是直线上的两点,若,则
2.在平面直角坐标系中,点,,点,点,若,,围成的三角形面积为,则点的坐标为( )
A. B.
C.或 D.或
3.若直线与的交点在第一象限,则的值可以是( )
A.1 B.2 C.3 D.
4.如图,在中,点E和F分别是上一点,,的平分线交于点D,是的外角,若,,,则α、β、γ三者间的数量关系是( )
A. B. C. D.
5.老师布置了一份家庭作业:用三根小木棍首尾相连拼出一个三角形,三根小木棍的长度分别为5、9、10.5,并且只能对10.5的小木棍进行裁切(裁切后,参与拼图的小木棍的长度为整数),则同学们最多能拼出不同的三角形的个数为( )
A.4 B.5 C.6 D.7
6.在平面直角坐标系中,一次函数 和 ,无论 取何值,始终有 , 的取值范围为( )
A. B. C. 且 D. 且
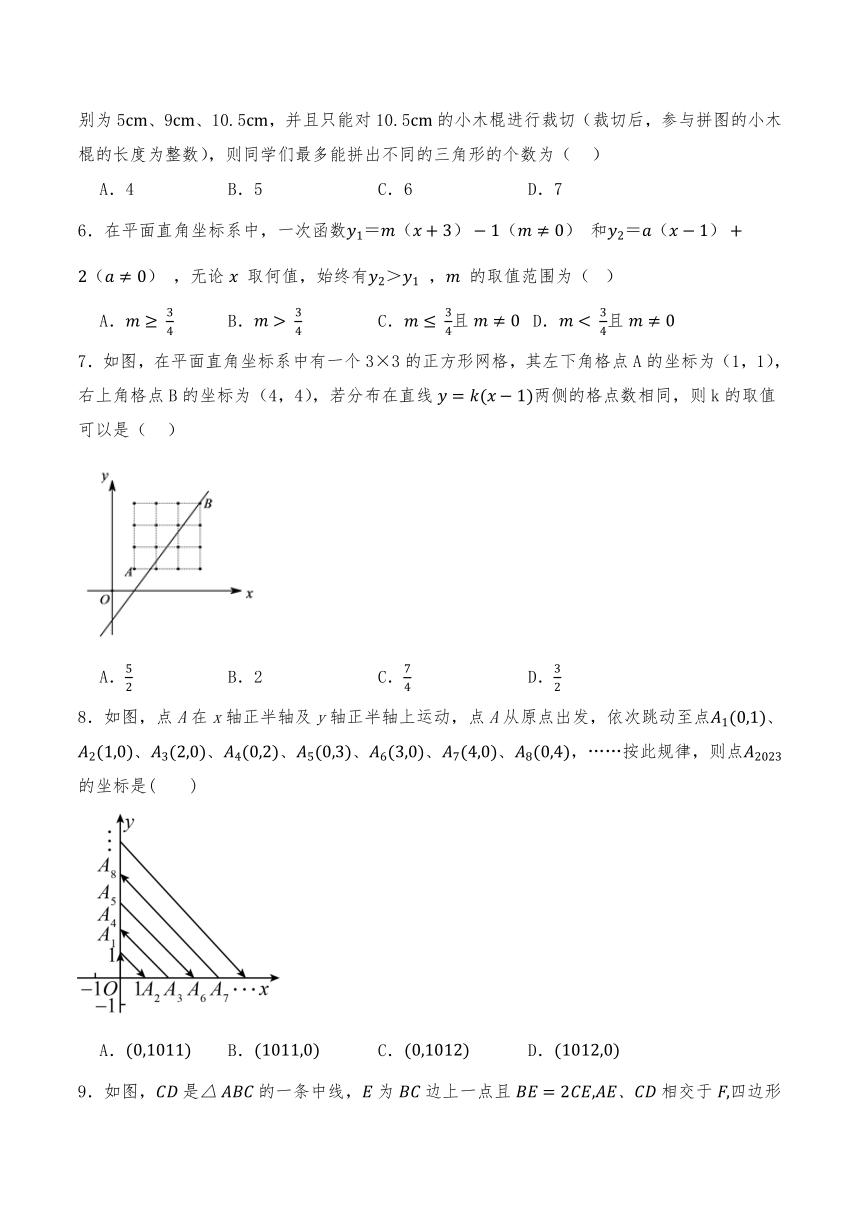
7.如图,在平面直角坐标系中有一个3×3的正方形网格,其左下角格点A的坐标为(1,1),右上角格点B的坐标为(4,4),若分布在直线两侧的格点数相同,则k的取值可以是( )
A. B.2 C. D.
8.如图,点A在x轴正半轴及y轴正半轴上运动,点A从原点出发,依次跳动至点、、、、、、、,……按此规律,则点的坐标是( )
A. B. C. D.
9.如图,是的一条中线,为边上一点且相交于四边形的面积为,则的面积是( )
A. B. C. D.
10.如图①,将一副三角板中的两个直角叠放在一起,其中,,,,现按住三角板不动,将三角板绕点C顺时针旋转,图②是旋转过程中的某一位置,当B、C、E三点第一次共线时旋转停止,记(k为常数),给出下列四个说法:
①当时,直线与直线相交所成的锐角度数为;
②当时,;
③当时,;
④当时,.其中正确的说法的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分,每小题3分)
11.已知线段轴,若点的坐标为,线段的长为4,则点的坐标是 .
12.如果直线与两坐标轴所围成的三角形的面积是9,那么的值为 .
13.下列命题中:①两条直线被第三条直线所截,同位角相等;②过一点有且只有一条直线与已知直线平行;③若的两边与的两边分别平行,则或;④若,则.其中假命题的是 (填写序号).
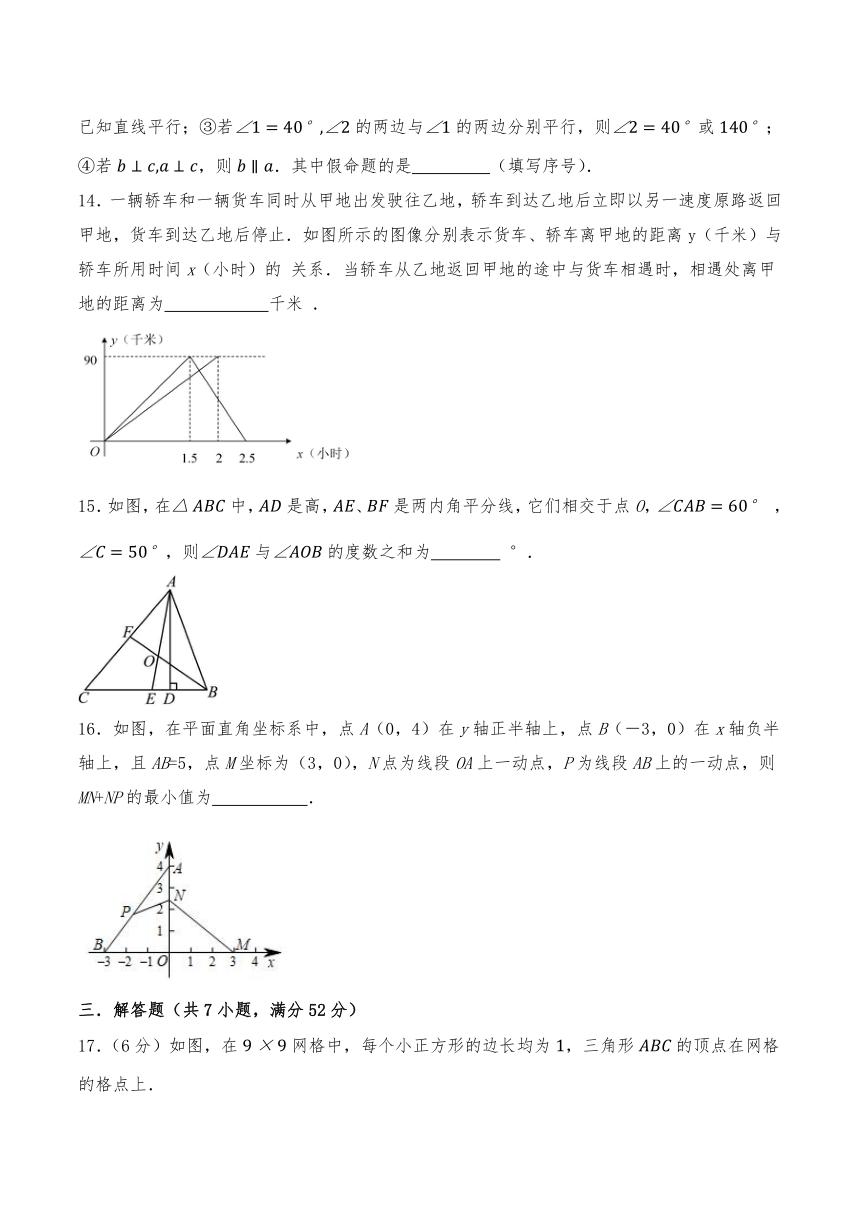
14.一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图像分别表示货车、轿车离甲地的距离y(千米)与轿车所用时间x(小时)的 关系.当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离为 千米 .
15.如图,在中,是高,、是两内角平分线,它们相交于点O, ,,则与的度数之和为 °.
16.如图,在平面直角坐标系中,点A(0,4)在y轴正半轴上,点B(-3,0)在x轴负半轴上,且AB=5,点M坐标为(3,0),N点为线段OA上一动点,P为线段AB上的一动点,则MN+NP的最小值为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,在网格中,每个小正方形的边长均为,三角形的顶点在网格的格点上.
(1)将三角形先向右平移个单位,再向下平移个单位长度,点,,的对应点依次为,,,画出三角形;
(2)以点为原点建立平面直角坐标系,写出,,,,五个点的坐标.
18.(6分)已知关于、的方程组
(1)若x、y满足不等式,求符合条件的m的非负整数值;
(2)若解x、y的值是一个等腰三角形两边的长,且这个等腰三角形的周长为21,求这个等腰三角形的腰长.
19.(8分)如图,在中,平分,为线段上的一点,过点作交直线于点.
(1)若,,求的度数;
(2)若,,求的度数;
(3)请根据以上结果,直接写出与,之间的数量关系.
20.(8分)如图,在平面直角坐标系中,一次函数的图象经过点,且与正比例函数的图象交于点.
(1)求的值及一次函数的解析式;
(2)若正比例函数的图象向上平移个单位长度后经过点.求的值;
(3)直接写出关于的不等式的解集.
21.(8分)从甲地到乙地,先是一段上坡路,然后是一段平路,小冲骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小冲骑车在上坡、平路、下坡时分别保持匀速前进,已知小冲骑车上坡的速度比平路上的速度每小时少,下坡的速度比在平路上的速度每小时多,设小冲出发x h后,到达离乙地的地方,图中的折线ABCDEF表示y与x之间的函数关系.
(1)求小冲在平路上骑车的平均速度以及他在乙地的休息时间;
(2)分别求线段所对应的函数关系式;
(3)从甲地到乙地经过丙地,如果小冲两次经过丙地的时间间隔为,求丙地与甲地之间的路程.
22.(8分)在平面直角坐标系中,,,,满足,连接交轴于.
(1)求与的值.
(2)如图1,点是轴上一点,且三角形的面积为12,求点的坐标;
(3)如图2,直线交轴于,将直线平移经过点,交轴于,点在直线上,且,直接写出点横坐标的值.
23.(8分)如图1,直线与直线,分别交于,两点,点在直线上,射线平分交直线于点,.
(1)求证:直线 ;
(2)如图2,点在直线上(点左侧),平分交于点,过点作交于点,请猜想与的关系;并证明你的结论;
(3)若点是线段上一点,射线交直线于点,.点在射线上,且满足连接,请补全图形,探究与满足的等量关系,并证明.
答案
一.选择题
1.C
【分析】由直线的图象可知,即可判断A;又可得出,即得出直线经过第一、二、四象限,可判断B;进而由一次函数的性质可判断D;由直线与坐标轴交点的横坐标即为其相关一元一次方程的解,可判断C.
【详解】解:由图象可知直线经过第一、二、三象限,且与y轴的交点位于x轴上方,
∴,故A错误,不符合题意;
∵,
∴.
又∵,
∴直线经过第一、二、四象限,故B错误,不符合题意;
∵直线与x轴交于点,
∴关于x的方程的解为,故C正确,符合题意;
∵直线经过第第一、二、四象限,
∴y随x的增大而减小.
∵,
∴,故D错误,不符合题意.
故选:C.
2.C
【分析】根据已知得出,,点到轴的距离为,进而根据三角形的面积公式,即可求解.
【详解】解:点,,点,点,
,点到轴的距离为,
,
即,
,
点的坐标为或.
故选:C.
3.A
【分析】联立两个函数的解析式求出交点坐标,进而根据第一象限内点的坐标特点得到关于b的不等式组,求出不等式组的解集即可得解.
【详解】解方程组,得,
因为直线与的交点在第一象限,
所以,解得,
观察各选项,的值可以是1;
故选:A.
4.B
【分析】由平行线的性质可得,由三角形外角的性质可得,,据此可解.
【详解】解:∵,,
∴,
∵平分,
∴,
∵是的外角,
∴,
∵,
∴,
∵是的外角,
∴,
∵,
∴,
即,
故选B.
5.C
【分析】根据三角形的三边关系列出不等式组求解即可.
【详解】解:设从10.5的小木棍上裁剪的线段长度为x,
则,即,
∴整数x的值为5、6 、7 、8、9、10,
∴同学们最多能做出6个不同的三角形木架.
故选:C.
6.D
【分析】根据一次函数的图象和性质分别判断.
【详解】由题意可知:∵一次函数 的图象过定点 ,
一次函数 过定点 ,
∵①时, ,两直线平行时,始终有 ,
∴ .
②当 时,设经过点 的直线为 ,有
,
解得:
∴
∵一次函数 的图象过定点 ,
不论 取何值,始终有 ,
∴
∴综上解得: 或 .
即: 且
故选:D
7.C
【分析】根据每一选项给定的k值,分别进行讨论即可得.
【详解】解:A、当k=时,直线为y=(x-1),
当x=1时,y=0,当x=2时,y=,当x=3时,y=5,当x=4时,y=,此时直线左上侧有6个格点,右下侧有10个格点,故不符合题意;
B、当k=2时,直线为y=2(x-1),
当x=1时,y=0,当x=2时,y=2,当x=3时,y=4,当x=4时,y=6,此时直线左上侧有6个格点,右下侧有8个格点,故不符合题意;
C、当k=时,直线为y=(x-1),
当x=1时,y=0,当x=2时,y=,当x=3时,y=,当x=4时,y=,此时直线左上侧有8个格点,右下侧有8个格点,故符合题意;
D、当k=时,直线为y=(x-1),
当x=1时,y=0,当x=2时,y=,当x=3时,y=3,当x=4时,y=,此时直线左上侧有8个格点,右下侧有7个格点,故不符合题意,
故选C.
8.D
【分析】根据已知点的坐标特征,将连续的4个点看成一组,由第1组,第2组确定组内点的位置特征、点坐标与组序数的联系;以此类推,,故点是第506组的第3个点,则在x轴上,其非零坐标即横坐标为.
【详解】解:根据题意,将连续的4个点A看成一组,
第1组:A1(0,1),A2(1,0),A3(2,0),A4(0,2),其位置分别为y轴、x轴、x轴、y轴,前两个点的非零坐标为1,后两个点的非零坐标为2;其中,,;
第2组:A5(0,3),A6(3,0),A7(4,0),A8(0,4),其位置分别为y轴、x轴、x轴、y轴,前两个点的非零坐标为3,后两个点的非零坐标为4;其中,,;
……
以此类推,,
则点是第506组的第3个点,则在x轴上,其非零坐标即横坐标为,故点的坐标是;
故选:D.
9.B
【分析】连结BF,设S△BDF=x,则S△BEF=6-x,由CD是中线可以得到S△ADF=S△BDF,S△BDC=S△ADC,由BE=2CE可以得到S△CEF=S△BEF,S△ABE=S△ABC,进而可用两种方法表示△ABC的面积,由此可得方程,进而得解.
【详解】解:如图,连接BF,
设S△BDF=x,则S△BEF=6-x,
∵CD是中线,
∴S△ADF=S△BDF=x,S△BDC= S△ADC=△ABC,
∵BE=2CE,
∴S△CEF=S△BEF=(6-x),S△ABE=S△ABC,
∵S△BDC= S△ADC=△ABC,
∴S△ABC=2S△BDC
=2[x+(6-x)]
=18-x,
∵S△ABE=S△ABC,
∴S△ABC=S△ABE
=[2x+ (6-x)]
=1.5x+9,
∴18-x =1.5x+9,
解得:x=3.6,
∴S△ABC=18-x,
=18-3.6
=14.4,
故选:B.
10.C
【分析】先证明,然后求出当时,,由此按照图①求解即可判断(1);当时, 求得,,则,即可判断(2);当时,先求出,则,,即可判断(3);根据题意当时,只有如图②一种情况,据此判断(4)即可.
【详解】解:当三角板旋转角度小于度时,如题干图②,设直线与直线交于F,
∴,
∴,
当时,即,如图①所示,
∴,
∴;
当三角板旋转角度大于时,如图②所示,
∴,
∴当时,即,
∴,
∴此时在图中的位置,
∴,故(1)正确;
当三角板旋转角度小于度时,如图所示,
当时,,
∴,
∴,
∴,
∴,
∴;
当三角板旋转角的大于时,如图④所示,
同理可得,
∴,
∴,
∵,
∴,故(2)错误;
如图⑤所示,当时,
∵,
∴,
∴,,
∴,
∴,故(3)正确;
由于顺时针旋转到B、C、E共线时停止,
∴当时,只有如下图⑥一种情况,
∴,
∴,
∴,
∴,故(4)正确,
故选:C.
二.填空题
11.或
【分析】线段轴,把点向左或右平移4个单位即可得到点坐标.
【详解】解:线段轴,
点的纵坐标与点的纵坐标相同,
,
点的坐标是或.
故答案为或.
12./6和/和6
【分析】当时,,当时,可求,由,即可求解.
【详解】解:当时,,
当时,,
解得:,
,
,
解得:,
故答案:.
13.①②
【分析】逐个判断各个命题的真假即可.
【详解】解:①两条平行,同位角相等,故①为假命题,符合题意;
②过直线外一点有且只有一条直线与已知直线平行;故②为假命题,符合题意;
③若的两边与的两边分别平行,如图:则或;故③为真命题,不符合题意;
④若,则,故④为真命题,不符合题意;
综上:假命题有①②,
故答案为:①②.
14.
【分析】根据函数图象中的数据,可以求得y1与x之间的函数关系式及轿车返回时的速度,然后即可计算出相遇处到甲地的距离.
【详解】解:如图,设y1与x之间的函数关系式是y1=kx,
2k=90,
解得,k=45,
即y1与x之间的函数关系式是y1=45x;
由图象可得,
轿车返回时的速度为:90÷(2.5-1.5)=90(千米/小时),
设当轿车从乙地返回甲地的途中与货车相遇时,货车行驶的时间为ah,
45a+90(a-1.5)=90,
解得,a= ,
∴45×=75(千米),
即相遇处到甲地的距离是75千米.
故答案是:75.
15.125
【分析】先利用三角形内角和定理可求,在直角三角形中,求出;再根据角平分线定义可求、,可得的度数;然后利用三角形外角性质,可先求,再次利用三角形外角性质,求出,即可求得出答案.
【详解】解:∵ ,
∴,
又∵是高,
∴,
∴,
∵、是角平分线,
∴,,
∴,
∵,
∴,
∴.
故答案为:125.
16.
【分析】连接AM,根据点A(0,4),点B(-3,0),点M坐标为(3,0),得到OA=4,OB=3,OM=3,过M作MP⊥AB于P交OA于N,则此时,MN+NP的值最小,且MN+NP的最小值=MP,根据三角形的面积公式即可得到结论.
【详解】解:连接AM,
∵点A(0,4),点B(-3,0),点M坐标为(3,0),
∴OA=4,OB=3,OM=3,
过M作MP⊥AB于P交OA于N,
则此时,MN+NP的值最小,且MN+NP的最小值=MP,
∵, BM=6,OA=4,AB=5,
∴.
故答案为:.
三.解答题
17.(1)解:如图所示:
即为所求;
(2)解:由(1)中图知,,,,,.
18.解:(1)解关于x,y的方程组 ,得 ,
代入3x-y<-6得,3(m-3)-(m+3)<-6,
解得m<3,
所以符合条件的m的非负整数值为0,1,2;
(2)由(1)得 ,
当腰为x=m-3时,2(m-3)+m+3=21,
解得m=8,则x= m-3=5,y=m+3=11,
∴三角形的三边分别为:5、5、11,不符合三角形的三边关系;
当腰为y=m+3时,2(m+3)+ m-3=21,
解得m=6,则x= m-3=3,y=m+3=9,
∴三角形的三边分别为:9、9、3,符合三角形的三边关系,
∴这个等腰三角形的腰长为9.
故答案为(1)0,1,2;(2)腰长为9.
19.(1)解:,,
,
平分,
,
,
,
;
(2),,
,
,,
,
平分,
,
;
(3).
证明:如图:
设,,
平分,
,
,
,,
,
,
,
,
,
.
20.(1)解:正比例函数的图像经过点,
,解得,,
,
一次函数的图像经过点,,
,解得,,
一次函数的解析式为,
(2)正比例函数的图像向下平移个单位长度后经过点,
平移后的函数的解析式为,
,解得;
(3)解:当,,解得:,则
,
根据图像可知的解集为:.
21.解:(1)小冲骑车上坡的速度为:km/h,
平路上的速度为:km/h;
下坡的速度为:km/h,
平路上所用的时间为:h,
下坡所用的时间为:h,
所以小冲在乙地休息了:h;
(2)由题意可知:上坡的速度为km/h,下坡的速度为km/h,
所以线段所对应的函数关系式为:,
即.
线段所对应的函数关系式为.
即;
(3)由题意可知:小冲第一次经过丙地在段,第二次经过丙地在段,
设小冲出发小时第一次经过丙地,则小冲出发后小时第二次经过丙地,
,
解得:.
(千米).
答:丙地与甲地之间的距离为1千米.
22.(1)解:(1),
又,,
,
;
(2)过点作轴于,
设,
三角形的面积四边形的面积三角形的面积,
,
即,
解得:,
∴点的坐标为.
过点作轴于,
三角形的面积三角形的面积三角形的面积,
,
即
,
点的坐标为或.
(3)设点向左平移4个单位长度,向下平移4个单位长度到点,则点平移后的对应点恰好是点.连接、,过点作轴,
,
,
∵,
∴,即,
∴,
当点在第三象限时,,
,
解得:,
当点在第二象限时,
,
解得:,
当三角形的面积等于三角形面积的时,点的横坐标是或.
23.(1)证明:∵射线平分交直线于点,
∴
∴
∴
(2)解:∵平分,平分
∴
设
∵
∴
则,
∵,
∴,
∴;
(3)解:,理由如下,
补全图形,如图所示,①当在上时,
∵
设
∵,.
∴,.
∵平分,
∵,
∴
∴,
∴
②如图,当点在的延长线上时,
∵,
∴,
∵,
∴,
∴,
∴
一.选择题(共10小题,满分30分,每小题3分)
1.如图,直线与x轴交于点,下列说法正确的是( )
A.
B.直线经过第三象限
C.关于x的方程的解为
D.若,是直线上的两点,若,则
2.在平面直角坐标系中,点,,点,点,若,,围成的三角形面积为,则点的坐标为( )
A. B.
C.或 D.或
3.若直线与的交点在第一象限,则的值可以是( )
A.1 B.2 C.3 D.
4.如图,在中,点E和F分别是上一点,,的平分线交于点D,是的外角,若,,,则α、β、γ三者间的数量关系是( )
A. B. C. D.
5.老师布置了一份家庭作业:用三根小木棍首尾相连拼出一个三角形,三根小木棍的长度分别为5、9、10.5,并且只能对10.5的小木棍进行裁切(裁切后,参与拼图的小木棍的长度为整数),则同学们最多能拼出不同的三角形的个数为( )
A.4 B.5 C.6 D.7
6.在平面直角坐标系中,一次函数 和 ,无论 取何值,始终有 , 的取值范围为( )
A. B. C. 且 D. 且
7.如图,在平面直角坐标系中有一个3×3的正方形网格,其左下角格点A的坐标为(1,1),右上角格点B的坐标为(4,4),若分布在直线两侧的格点数相同,则k的取值可以是( )
A. B.2 C. D.
8.如图,点A在x轴正半轴及y轴正半轴上运动,点A从原点出发,依次跳动至点、、、、、、、,……按此规律,则点的坐标是( )
A. B. C. D.
9.如图,是的一条中线,为边上一点且相交于四边形的面积为,则的面积是( )
A. B. C. D.
10.如图①,将一副三角板中的两个直角叠放在一起,其中,,,,现按住三角板不动,将三角板绕点C顺时针旋转,图②是旋转过程中的某一位置,当B、C、E三点第一次共线时旋转停止,记(k为常数),给出下列四个说法:
①当时,直线与直线相交所成的锐角度数为;
②当时,;
③当时,;
④当时,.其中正确的说法的个数是( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共6小题,满分18分,每小题3分)
11.已知线段轴,若点的坐标为,线段的长为4,则点的坐标是 .
12.如果直线与两坐标轴所围成的三角形的面积是9,那么的值为 .
13.下列命题中:①两条直线被第三条直线所截,同位角相等;②过一点有且只有一条直线与已知直线平行;③若的两边与的两边分别平行,则或;④若,则.其中假命题的是 (填写序号).
14.一辆轿车和一辆货车同时从甲地出发驶往乙地,轿车到达乙地后立即以另一速度原路返回甲地,货车到达乙地后停止.如图所示的图像分别表示货车、轿车离甲地的距离y(千米)与轿车所用时间x(小时)的 关系.当轿车从乙地返回甲地的途中与货车相遇时,相遇处离甲地的距离为 千米 .
15.如图,在中,是高,、是两内角平分线,它们相交于点O, ,,则与的度数之和为 °.
16.如图,在平面直角坐标系中,点A(0,4)在y轴正半轴上,点B(-3,0)在x轴负半轴上,且AB=5,点M坐标为(3,0),N点为线段OA上一动点,P为线段AB上的一动点,则MN+NP的最小值为 .
三.解答题(共7小题,满分52分)
17.(6分)如图,在网格中,每个小正方形的边长均为,三角形的顶点在网格的格点上.
(1)将三角形先向右平移个单位,再向下平移个单位长度,点,,的对应点依次为,,,画出三角形;
(2)以点为原点建立平面直角坐标系,写出,,,,五个点的坐标.
18.(6分)已知关于、的方程组
(1)若x、y满足不等式,求符合条件的m的非负整数值;
(2)若解x、y的值是一个等腰三角形两边的长,且这个等腰三角形的周长为21,求这个等腰三角形的腰长.
19.(8分)如图,在中,平分,为线段上的一点,过点作交直线于点.
(1)若,,求的度数;
(2)若,,求的度数;
(3)请根据以上结果,直接写出与,之间的数量关系.
20.(8分)如图,在平面直角坐标系中,一次函数的图象经过点,且与正比例函数的图象交于点.
(1)求的值及一次函数的解析式;
(2)若正比例函数的图象向上平移个单位长度后经过点.求的值;
(3)直接写出关于的不等式的解集.
21.(8分)从甲地到乙地,先是一段上坡路,然后是一段平路,小冲骑车从甲地出发,到达乙地后休息一段时间,然后原路返回甲地.假设小冲骑车在上坡、平路、下坡时分别保持匀速前进,已知小冲骑车上坡的速度比平路上的速度每小时少,下坡的速度比在平路上的速度每小时多,设小冲出发x h后,到达离乙地的地方,图中的折线ABCDEF表示y与x之间的函数关系.
(1)求小冲在平路上骑车的平均速度以及他在乙地的休息时间;
(2)分别求线段所对应的函数关系式;
(3)从甲地到乙地经过丙地,如果小冲两次经过丙地的时间间隔为,求丙地与甲地之间的路程.
22.(8分)在平面直角坐标系中,,,,满足,连接交轴于.
(1)求与的值.
(2)如图1,点是轴上一点,且三角形的面积为12,求点的坐标;
(3)如图2,直线交轴于,将直线平移经过点,交轴于,点在直线上,且,直接写出点横坐标的值.
23.(8分)如图1,直线与直线,分别交于,两点,点在直线上,射线平分交直线于点,.
(1)求证:直线 ;
(2)如图2,点在直线上(点左侧),平分交于点,过点作交于点,请猜想与的关系;并证明你的结论;
(3)若点是线段上一点,射线交直线于点,.点在射线上,且满足连接,请补全图形,探究与满足的等量关系,并证明.
答案
一.选择题
1.C
【分析】由直线的图象可知,即可判断A;又可得出,即得出直线经过第一、二、四象限,可判断B;进而由一次函数的性质可判断D;由直线与坐标轴交点的横坐标即为其相关一元一次方程的解,可判断C.
【详解】解:由图象可知直线经过第一、二、三象限,且与y轴的交点位于x轴上方,
∴,故A错误,不符合题意;
∵,
∴.
又∵,
∴直线经过第一、二、四象限,故B错误,不符合题意;
∵直线与x轴交于点,
∴关于x的方程的解为,故C正确,符合题意;
∵直线经过第第一、二、四象限,
∴y随x的增大而减小.
∵,
∴,故D错误,不符合题意.
故选:C.
2.C
【分析】根据已知得出,,点到轴的距离为,进而根据三角形的面积公式,即可求解.
【详解】解:点,,点,点,
,点到轴的距离为,
,
即,
,
点的坐标为或.
故选:C.
3.A
【分析】联立两个函数的解析式求出交点坐标,进而根据第一象限内点的坐标特点得到关于b的不等式组,求出不等式组的解集即可得解.
【详解】解方程组,得,
因为直线与的交点在第一象限,
所以,解得,
观察各选项,的值可以是1;
故选:A.
4.B
【分析】由平行线的性质可得,由三角形外角的性质可得,,据此可解.
【详解】解:∵,,
∴,
∵平分,
∴,
∵是的外角,
∴,
∵,
∴,
∵是的外角,
∴,
∵,
∴,
即,
故选B.
5.C
【分析】根据三角形的三边关系列出不等式组求解即可.
【详解】解:设从10.5的小木棍上裁剪的线段长度为x,
则,即,
∴整数x的值为5、6 、7 、8、9、10,
∴同学们最多能做出6个不同的三角形木架.
故选:C.
6.D
【分析】根据一次函数的图象和性质分别判断.
【详解】由题意可知:∵一次函数 的图象过定点 ,
一次函数 过定点 ,
∵①时, ,两直线平行时,始终有 ,
∴ .
②当 时,设经过点 的直线为 ,有
,
解得:
∴
∵一次函数 的图象过定点 ,
不论 取何值,始终有 ,
∴
∴综上解得: 或 .
即: 且
故选:D
7.C
【分析】根据每一选项给定的k值,分别进行讨论即可得.
【详解】解:A、当k=时,直线为y=(x-1),
当x=1时,y=0,当x=2时,y=,当x=3时,y=5,当x=4时,y=,此时直线左上侧有6个格点,右下侧有10个格点,故不符合题意;
B、当k=2时,直线为y=2(x-1),
当x=1时,y=0,当x=2时,y=2,当x=3时,y=4,当x=4时,y=6,此时直线左上侧有6个格点,右下侧有8个格点,故不符合题意;
C、当k=时,直线为y=(x-1),
当x=1时,y=0,当x=2时,y=,当x=3时,y=,当x=4时,y=,此时直线左上侧有8个格点,右下侧有8个格点,故符合题意;
D、当k=时,直线为y=(x-1),
当x=1时,y=0,当x=2时,y=,当x=3时,y=3,当x=4时,y=,此时直线左上侧有8个格点,右下侧有7个格点,故不符合题意,
故选C.
8.D
【分析】根据已知点的坐标特征,将连续的4个点看成一组,由第1组,第2组确定组内点的位置特征、点坐标与组序数的联系;以此类推,,故点是第506组的第3个点,则在x轴上,其非零坐标即横坐标为.
【详解】解:根据题意,将连续的4个点A看成一组,
第1组:A1(0,1),A2(1,0),A3(2,0),A4(0,2),其位置分别为y轴、x轴、x轴、y轴,前两个点的非零坐标为1,后两个点的非零坐标为2;其中,,;
第2组:A5(0,3),A6(3,0),A7(4,0),A8(0,4),其位置分别为y轴、x轴、x轴、y轴,前两个点的非零坐标为3,后两个点的非零坐标为4;其中,,;
……
以此类推,,
则点是第506组的第3个点,则在x轴上,其非零坐标即横坐标为,故点的坐标是;
故选:D.
9.B
【分析】连结BF,设S△BDF=x,则S△BEF=6-x,由CD是中线可以得到S△ADF=S△BDF,S△BDC=S△ADC,由BE=2CE可以得到S△CEF=S△BEF,S△ABE=S△ABC,进而可用两种方法表示△ABC的面积,由此可得方程,进而得解.
【详解】解:如图,连接BF,
设S△BDF=x,则S△BEF=6-x,
∵CD是中线,
∴S△ADF=S△BDF=x,S△BDC= S△ADC=△ABC,
∵BE=2CE,
∴S△CEF=S△BEF=(6-x),S△ABE=S△ABC,
∵S△BDC= S△ADC=△ABC,
∴S△ABC=2S△BDC
=2[x+(6-x)]
=18-x,
∵S△ABE=S△ABC,
∴S△ABC=S△ABE
=[2x+ (6-x)]
=1.5x+9,
∴18-x =1.5x+9,
解得:x=3.6,
∴S△ABC=18-x,
=18-3.6
=14.4,
故选:B.
10.C
【分析】先证明,然后求出当时,,由此按照图①求解即可判断(1);当时, 求得,,则,即可判断(2);当时,先求出,则,,即可判断(3);根据题意当时,只有如图②一种情况,据此判断(4)即可.
【详解】解:当三角板旋转角度小于度时,如题干图②,设直线与直线交于F,
∴,
∴,
当时,即,如图①所示,
∴,
∴;
当三角板旋转角度大于时,如图②所示,
∴,
∴当时,即,
∴,
∴此时在图中的位置,
∴,故(1)正确;
当三角板旋转角度小于度时,如图所示,
当时,,
∴,
∴,
∴,
∴,
∴;
当三角板旋转角的大于时,如图④所示,
同理可得,
∴,
∴,
∵,
∴,故(2)错误;
如图⑤所示,当时,
∵,
∴,
∴,,
∴,
∴,故(3)正确;
由于顺时针旋转到B、C、E共线时停止,
∴当时,只有如下图⑥一种情况,
∴,
∴,
∴,
∴,故(4)正确,
故选:C.
二.填空题
11.或
【分析】线段轴,把点向左或右平移4个单位即可得到点坐标.
【详解】解:线段轴,
点的纵坐标与点的纵坐标相同,
,
点的坐标是或.
故答案为或.
12./6和/和6
【分析】当时,,当时,可求,由,即可求解.
【详解】解:当时,,
当时,,
解得:,
,
,
解得:,
故答案:.
13.①②
【分析】逐个判断各个命题的真假即可.
【详解】解:①两条平行,同位角相等,故①为假命题,符合题意;
②过直线外一点有且只有一条直线与已知直线平行;故②为假命题,符合题意;
③若的两边与的两边分别平行,如图:则或;故③为真命题,不符合题意;
④若,则,故④为真命题,不符合题意;
综上:假命题有①②,
故答案为:①②.
14.
【分析】根据函数图象中的数据,可以求得y1与x之间的函数关系式及轿车返回时的速度,然后即可计算出相遇处到甲地的距离.
【详解】解:如图,设y1与x之间的函数关系式是y1=kx,
2k=90,
解得,k=45,
即y1与x之间的函数关系式是y1=45x;
由图象可得,
轿车返回时的速度为:90÷(2.5-1.5)=90(千米/小时),
设当轿车从乙地返回甲地的途中与货车相遇时,货车行驶的时间为ah,
45a+90(a-1.5)=90,
解得,a= ,
∴45×=75(千米),
即相遇处到甲地的距离是75千米.
故答案是:75.
15.125
【分析】先利用三角形内角和定理可求,在直角三角形中,求出;再根据角平分线定义可求、,可得的度数;然后利用三角形外角性质,可先求,再次利用三角形外角性质,求出,即可求得出答案.
【详解】解:∵ ,
∴,
又∵是高,
∴,
∴,
∵、是角平分线,
∴,,
∴,
∵,
∴,
∴.
故答案为:125.
16.
【分析】连接AM,根据点A(0,4),点B(-3,0),点M坐标为(3,0),得到OA=4,OB=3,OM=3,过M作MP⊥AB于P交OA于N,则此时,MN+NP的值最小,且MN+NP的最小值=MP,根据三角形的面积公式即可得到结论.
【详解】解:连接AM,
∵点A(0,4),点B(-3,0),点M坐标为(3,0),
∴OA=4,OB=3,OM=3,
过M作MP⊥AB于P交OA于N,
则此时,MN+NP的值最小,且MN+NP的最小值=MP,
∵, BM=6,OA=4,AB=5,
∴.
故答案为:.
三.解答题
17.(1)解:如图所示:
即为所求;
(2)解:由(1)中图知,,,,,.
18.解:(1)解关于x,y的方程组 ,得 ,
代入3x-y<-6得,3(m-3)-(m+3)<-6,
解得m<3,
所以符合条件的m的非负整数值为0,1,2;
(2)由(1)得 ,
当腰为x=m-3时,2(m-3)+m+3=21,
解得m=8,则x= m-3=5,y=m+3=11,
∴三角形的三边分别为:5、5、11,不符合三角形的三边关系;
当腰为y=m+3时,2(m+3)+ m-3=21,
解得m=6,则x= m-3=3,y=m+3=9,
∴三角形的三边分别为:9、9、3,符合三角形的三边关系,
∴这个等腰三角形的腰长为9.
故答案为(1)0,1,2;(2)腰长为9.
19.(1)解:,,
,
平分,
,
,
,
;
(2),,
,
,,
,
平分,
,
;
(3).
证明:如图:
设,,
平分,
,
,
,,
,
,
,
,
,
.
20.(1)解:正比例函数的图像经过点,
,解得,,
,
一次函数的图像经过点,,
,解得,,
一次函数的解析式为,
(2)正比例函数的图像向下平移个单位长度后经过点,
平移后的函数的解析式为,
,解得;
(3)解:当,,解得:,则
,
根据图像可知的解集为:.
21.解:(1)小冲骑车上坡的速度为:km/h,
平路上的速度为:km/h;
下坡的速度为:km/h,
平路上所用的时间为:h,
下坡所用的时间为:h,
所以小冲在乙地休息了:h;
(2)由题意可知:上坡的速度为km/h,下坡的速度为km/h,
所以线段所对应的函数关系式为:,
即.
线段所对应的函数关系式为.
即;
(3)由题意可知:小冲第一次经过丙地在段,第二次经过丙地在段,
设小冲出发小时第一次经过丙地,则小冲出发后小时第二次经过丙地,
,
解得:.
(千米).
答:丙地与甲地之间的距离为1千米.
22.(1)解:(1),
又,,
,
;
(2)过点作轴于,
设,
三角形的面积四边形的面积三角形的面积,
,
即,
解得:,
∴点的坐标为.
过点作轴于,
三角形的面积三角形的面积三角形的面积,
,
即
,
点的坐标为或.
(3)设点向左平移4个单位长度,向下平移4个单位长度到点,则点平移后的对应点恰好是点.连接、,过点作轴,
,
,
∵,
∴,即,
∴,
当点在第三象限时,,
,
解得:,
当点在第二象限时,
,
解得:,
当三角形的面积等于三角形面积的时,点的横坐标是或.
23.(1)证明:∵射线平分交直线于点,
∴
∴
∴
(2)解:∵平分,平分
∴
设
∵
∴
则,
∵,
∴,
∴;
(3)解:,理由如下,
补全图形,如图所示,①当在上时,
∵
设
∵,.
∴,.
∵平分,
∵,
∴
∴,
∴
②如图,当点在的延长线上时,
∵,
∴,
∵,
∴,
∴,
∴
同课章节目录
