沪科版八年级数学下册试题 期末检测卷(含解析)
文档属性
| 名称 | 沪科版八年级数学下册试题 期末检测卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 675.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 15:08:34 | ||
图片预览


文档简介
期末检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列运算正确的是( )
A. B. C. D.
2.函数中,自变量x的取值范围是( )
A. B.
C.且 D.且
3. 在学校数学学科知识竞赛中,我班“”组的6个同学获得的分数分别为:95、97、97、96、98、95,对于这6个同学的成绩下列说法正确的是( )
A.众数为95 B.众数为97 C.平均数为96 D.极差为3
4.若关于x的一元二次方程有两个不相等实数根,则k的取值范围是( )
A.且 B. C. D.
5.如图,是某月的日历表,在此日历表上可以用一个矩形圈出个位置相邻的数(如6,7,8,13,14,15,20,21,22).如果圈出的9个数中,最小数x与最大数的积为161,那么根据题意可列方程为( )
A. B.
C. D.
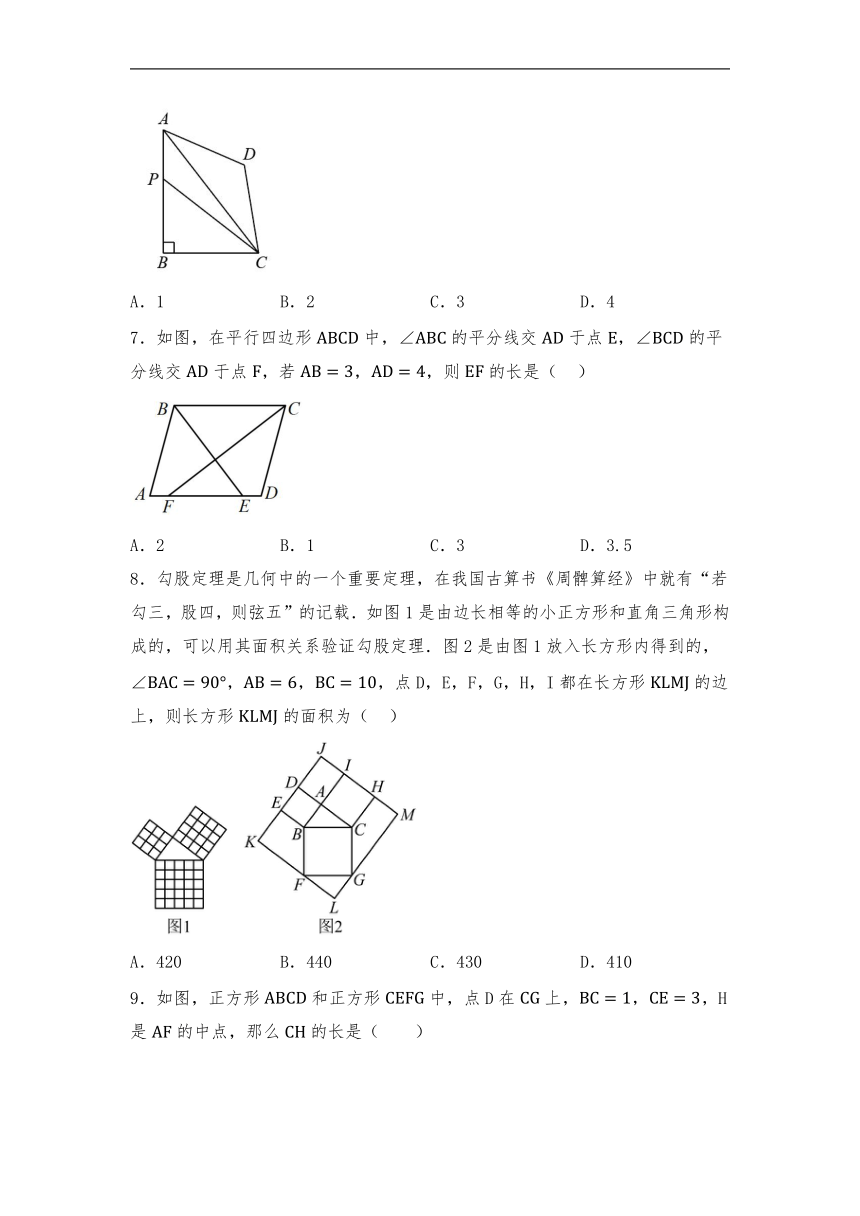
6.如图,在四边形中,,,,,点在四边形的边上,若的面积为120,则满足条件的点的个数为( )
A.1 B.2 C.3 D.4
7.如图,在平行四边形中,的平分线交于点,的平分线交于点,若,,则的长是( )
A.2 B.1 C.3 D.3.5
8.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的, ,点D,E,F,G,H,I都在长方形的边上,则长方形的面积为( )
A.420 B.440 C.430 D.410
9.如图,正方形和正方形中,点D在上,,H是的中点,那么的长是( )
A.2.5 B. C. D.2
10.如图,在正方形中,为对角线,为上一点,过点作,与、分别交于点,,为的中点,连接,,,,下列结论中结论正确的有( )
①;②;③;④若,则,其中结论正确的有( )
A.个 B.个 C.个 D.个
二.填空题(共6小题,满分18分,每小题3分)
11.与最简二次根式是同类二次根式,则a=_____.
12.某中学随机抽查了50名学生,了解他们平均每天的睡眠时间,结果如下表所示:
时间(小时) 6 7 8 9
人数 3 6 32 9
根据学生睡眠管理相关规定﹐初中学生平均每天睡眠时间不低于8小时,该校共有学生2000人,试估计该校学生睡眠时间符合要求的约有______人.
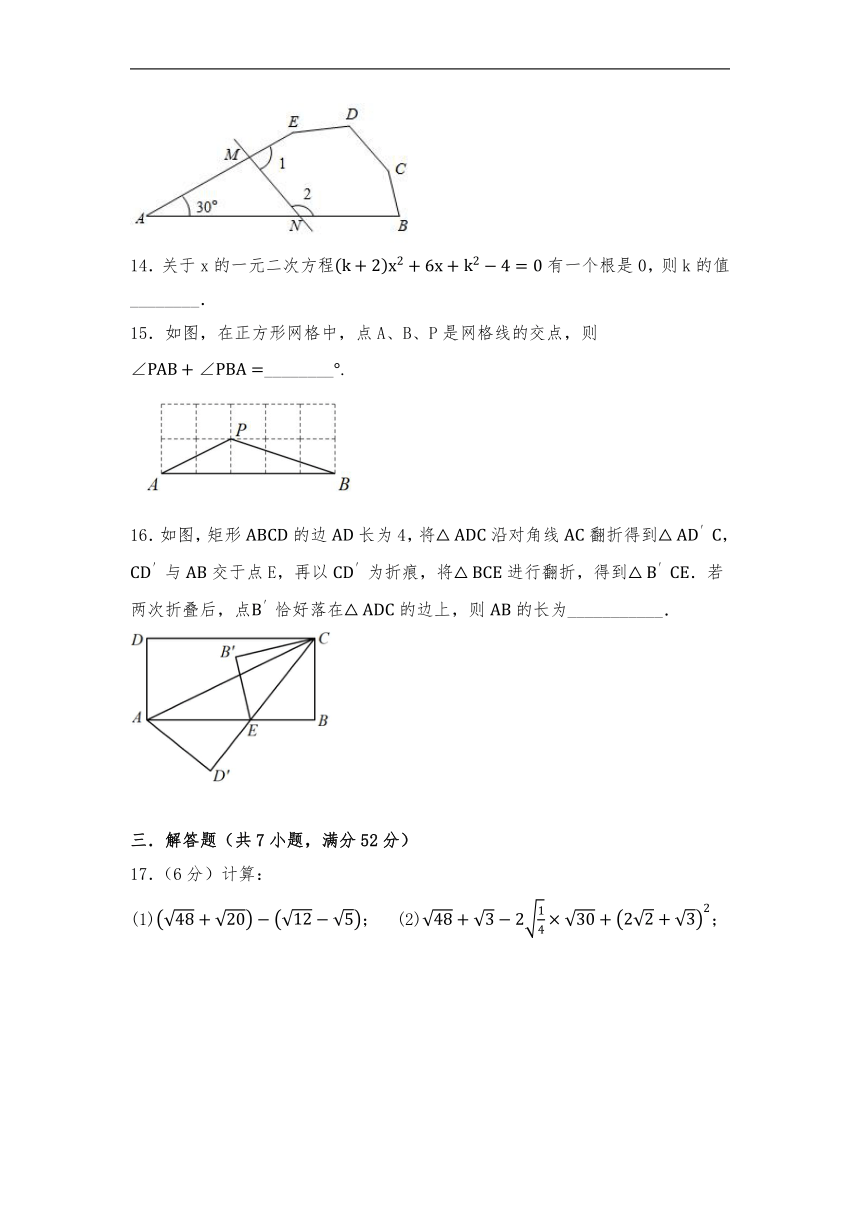
13.如图,在五边形中,若去掉一个的角后得到一个六边形,则的度数为____________.
14.关于x的一元二次方程有一个根是0,则k的值________.
15.如图,在正方形网格中,点A、B、P是网格线的交点,则________.
16.如图,矩形的边长为4,将沿对角线翻折得到,与交于点E,再以为折痕,将进行翻折,得到.若两次折叠后,点恰好落在的边上,则的长为___________.
三.解答题(共7小题,满分52分)
17.(6分)计算:
(1); (2);
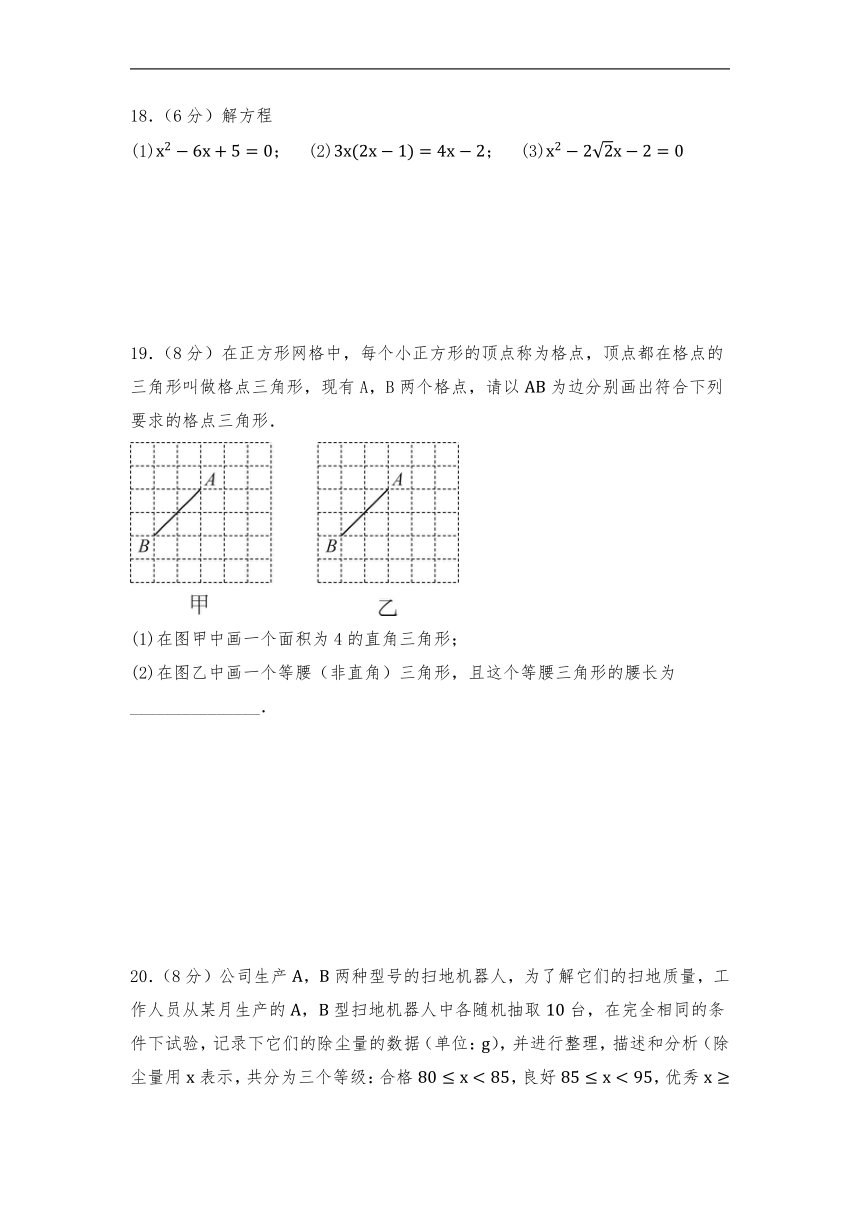
18.(6分)解方程
(1); (2); (3)
19.(8分)在正方形网格中,每个小正方形的顶点称为格点,顶点都在格点的三角形叫做格点三角形,现有A,B两个格点,请以为边分别画出符合下列要求的格点三角形.
(1)在图甲中画一个面积为4的直角三角形;
(2)在图乙中画一个等腰(非直角)三角形,且这个等腰三角形的腰长为_______________.
20.(8分)公司生产,两种型号的扫地机器人,为了解它们的扫地质量,工作人员从某月生产的,型扫地机器人中各随机抽取台,在完全相同的条件下试验,记录下它们的除尘量的数据(单位:),并进行整理,描述和分析(除尘量用表示,共分为三个等级:合格,良好,优秀),下面给出了部分信息:
台型扫地机器人的除尘量:,,,,,,,,,.
台型扫地机器人中良好等级包含的所有数据:,,,,.
抽取的,型扫地机器人除尘量统计表
型号 平均数 中位数 众数 方差 “优秀”等级所占百分比
根据以上信息,解答下列问题.
(1)填空:______,_______,_______;
(2)这个月公司生产B型扫地机器人共3000台,估计该月B型扫地机器人“优秀”等级的台数.
(3)根据以上数据,你认为该公司生产的哪种型号的扫地机器人扫地质量更好?请说明理由(写出一条理由即可).
21.(8分)世界杯是世界上级别最高的足球赛事,2023年世界杯在卡塔尔隆重举行,今年世界杯的吉样物是“拉伊卜”,它的设计灵感来源于阿拉伯标志型的白头巾,某网店现售有一大一小两种型号的“拉伊卜”摆件,已知每个大摆件的售价是每个小摆件售价的2倍还多60元,420元可购买一个大摆件和一个小摆件.
(1)每个“拉伊卜”大摆件和小摆件的售价分别是多少?
(2)第一天该网店按照原售价卖出大摆件30个,小摆件100个,因为小摆件库存量大,第二天商家调整了销售方案,大摆件的价格不变,小摆件的价格下调元,调整后,当天大摆件的销量下降了个,小摆件的销量增加了个,当天的销售额达到了20520元,求降价后的小摆件的价格.
22.(8分)在长方形中,,,点是边上的一点,将沿折叠,点的对应点为点,射线与线段交于点.
(1)如图,当点和点重合时,求证:;
(2)如图,当点正好落在矩形的对角线上时,求的长度;
(3)如图,连接,,若,求的面积.
23.(8分)中,D、E分别是,的中点,O是内任意一点,连接、.
(1)如图1,点G、F分别是、的中点,连接,,,,求证:四边形是平行四边形;
(2)如图2,若点O恰为和交点,求证:,;
(3)如图3,若点O恰为和交点,射线与交于点M,求证:.
答案
一.选择题
1.D
【分析】根据二次根式的加减乘除四则运算法则,逐项判断即可求解.
【详解】解:A、和不是同类二次根式,无法合并,故本选项错误,不符合题意;
B、,故本选项错误,不符合题意;
C、,故本选项错误,不符合题意;
D、,故本选项正确,符合题意;
故选:D
2.D
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不为0,列不等式组可求得自变量的取值范围.
【详解】根据题意得:
解得:且
故选:D.
3.D
【分析】根据一组数据中出现次数最多的为众数,所有数据和除以数据的个数为平均数,最大数减最小数为极差,逐一进行判断即可.
【详解】解:A、两个数据各出现两次,众数为,选项错误,不符合题意;
B、两个数据各出现两次,众数为,选项错误,不符合题意;
C、,选项错误,不符合题意;
D、极差为:,选项正确,符合题意;
故选D.
4.A
【分析】依据一元二次方程的定义得,及一元二次方程有两个不相等实数根时,求解不等式即可.
【详解】解:依题意得,
且,
解得:且,
故选:A.
5.B
【分析】根据日历上数字规律得出,圈出的9个数,最大数与最小数的差为16,以及利用最大数与最小数的积为161,列出方程即可.
【详解】解:根据图表可以得出,圈出的9个数,最大数与最小数的差为16,设最小数为,则最大数为,
根据题意得出:,
故选:B.
6.C
【分析】根据三角形的面积和三角形面积,可以判断点可能存在线段和线段上;根据点在四边形的边上,考虑此时点存在和上,利用勾股定理和等腰三角形的性质分别求出长度和三角形的高,从而求出三角形的面积,发现与三角形面积相等,从而推出点在点处.
【详解】解:, ,
.
.
当点在边上,如图所示:
,
.
.
此时点满足条件.
当点在边上,如图所示:
,
.
.
此时点满足条件.
过点作于点,
,,
中,.
,,
.
中,
点在四边形的边上,
点和点重合,
点在点处.
满足条件的点共3个.
故答案选:.
7.A
【分析】根据平行四边形的性质证明,,进而可得和的长,然后可得答案.
【详解】解:四边形是平行四边形,
,,,
,
又平分,
,
,
,
同理可证:,
,
,
.
故选:A.
8.B
【分析】延长交于P,延长交于Q,可得全等,根据全等三角形对应边相等可得,然后求出和的长,再根据长方形的面积公式列式计算即可得解.
【详解】解:如图,延长交于P,延长交于Q,
由题意得,,
∴,
∴,
∴,
同理可证,
∴,
∵图2是由图1放入长方形内得到,
∴,,
∴长方形的面积.
故选:B.
9.B
【分析】连接,如图,根据正方形的性质得,则,再利用勾股定理计算出,然后根据直角三角形斜边上的中线求的长.
【详解】解:如图,连接,
∵正方形和正方形中,
∴,,
,
∴,
由勾股定理得,,
∵H是的中点,
∴.
故选:B.
10.D
【分析】根据正方形,为对角线,,可知四边形是矩形,由此可证、
、、是等腰直角三角形,为的中点,,可知是等腰
直角三角形,由此即可求解.
【详解】解:结论①,
∵正方形中,为对角线,,
∴,,
∴,四边形是矩形,、是等腰直角三角形,
∴,
∴,故结论①正确;
结论②,
由结论①正确可知,是等腰直角三角形,为的中点,
∴,且、是等腰直角三角形,
∴,,,
∴,且,
∴,
∴,
∵,故结论②正确;
结论③,
∵、、、是等腰直角三角形,,
∴,
∵四边形是矩形,
∴,
∴,故结论③正确;
结论④若,则,
由结论②正确,可知;由结论③正确可知,,
且、、、是等腰直角三角形,
∴,即是等腰直角三角形,
如图所示,过点作于,设,则,,,
∴,,
∴,故结论④正确;
综上所示,正确的有①②③④,
故选:.
二.填空题(共6小题,满分18分,每小题3分)
11.3
【分析】首先化简二次根式,再根据同类二次根式定义可得2a﹣3=3,再解即可.
【详解】,
∵与最简二次根式是同类二次根式,
∴2a﹣3=3,
解得:a=3,
故答案为:3.
12.人
故答案为:1640.
13.
【分析】根据多边形的内角和定理可求得,,进而可求解.
【详解】解:∵,,
∴,
∵,
∴,
故答案为:
14.2
【分析】将代入方程,结合一元二次方程,,进行求解即可.
【详解】解:∵x的一元二次方程有一个根是0,
∴,
解得:
∵,是一元二次方程,
∴,
∴,
∴;
故答案为:2.
15.45
【分析】取网格上的点C、D、E,连接.利用全等三角形的性质和平行线的性质求得,再利用勾股定理及其逆定理求得,即证明为等腰直角三角形,便可解答.
【详解】解:如图,点C、D、E是网格线交点,连接,
由图可得,
∴,
∴,
∴,
∴;
设小网格的边长为a,由勾股定理可得:,
∵,
∴
∴,
∴,
∴.
故答案为:45.
16.或
【分析】根据题意分两种情况讨论:①当点恰好落在上时,由翻折以及矩形的性质利用可证明,然后根据等腰三角形的性质求出的长,再依据勾股定理求解即可;②当点恰好落在上时,同理利用可证明,根据全等三角形的性质可得出的长,再根据线段的和差关系即可得出答案.
【详解】∵四边形为矩形,
∴,,
∵沿对角线翻折得到,
∴,,
∵以为折痕,将进行翻折,得到,
∴,,
①当点恰好落在上时,如图,
在和中,
∴
∴,即为等腰三角形,
∵
∴点为中点,
∴,
在中,有,
即,解得
②当点恰好落在上时,如图,
∵
∴四边形为矩形,
∴,
∵沿进行翻折,得到,
∴
在中,
,
在和中,
∴≌()
∴
∴.
故答案为:或.
三.解答题
17.(1)
=
=
(2)
=
=
18.(1)
,,
∴,
(2)
∴,
(3)
∴
∴,
19.(1)解:为所求作的三角形,如图所示:
(画出一种情况即可)
(2)解:为所求作的三角形,如图所示:(画出一种情况即可)
图1和图2中腰长为;
图3中腰长为.
故答案为:(画图3填).
20.(1)解:型中除尘量为的有个,数量最多,
所以众数;
型中“良好”等级包含的数据有个,则所占百分比为,
所以,即;
因为型中“合格”等级所占百分比为,
所以型中“合格”的有个,
所以型中中位数b=;
故答案为:;;;
(2)(台),
答:估计该月型扫地机器人“优秀”等级的台数有台;
(3)型号更好,
理由:在平均数均为的情况下,型号的平均除尘量众数大于型号的平均除尘量众数90.
21.(1)解:设每个小摆件的售价为x元,则每个大摆件的售价为元,根据题意得:
,
解得:,
(元),
答:每个“拉伊卜”大摆件和小摆件的售价分别是300元和120元.
(2)解:调整后,当天大摆件的销量为个,小摆件的销量为个,小摆件的价格为元,根据题意得:
,
解得:,(舍去),
(元),
答:降价后的小摆件的价格为108元.
22.(1)证明:四边形是矩形,
,
,
由折叠得:,
,
;
(2)解:四边形是矩形,
,,
,
由折叠知:,,,
,,
,
,
,
设,则,
在中,由勾股定理得,
,
,
,
;
(3)如图,作于,交于,
,
,
,
四边形是矩形,
,
四边形是矩形,
,,,
在中,,,
,
,
.
23.(1)∵D,E分别是的边,的中点,
∴是的中位线,
∴,,
同理:,,
∴,,
∴四边形是平行四边形;
(2)取,中点G,F,连接,,,,
∴,,
由(1)知,四边形是平行四边形,
∴,,
∴,;
(3)在射线上截取,连接,,
∵D,O分别是,的中点,
∴是的中位线,
∴即,
同理:,
∴四边形是平行四边形,
∴.
一.选择题(共10小题,满分30分,每小题3分)
1.下列运算正确的是( )
A. B. C. D.
2.函数中,自变量x的取值范围是( )
A. B.
C.且 D.且
3. 在学校数学学科知识竞赛中,我班“”组的6个同学获得的分数分别为:95、97、97、96、98、95,对于这6个同学的成绩下列说法正确的是( )
A.众数为95 B.众数为97 C.平均数为96 D.极差为3
4.若关于x的一元二次方程有两个不相等实数根,则k的取值范围是( )
A.且 B. C. D.
5.如图,是某月的日历表,在此日历表上可以用一个矩形圈出个位置相邻的数(如6,7,8,13,14,15,20,21,22).如果圈出的9个数中,最小数x与最大数的积为161,那么根据题意可列方程为( )
A. B.
C. D.
6.如图,在四边形中,,,,,点在四边形的边上,若的面积为120,则满足条件的点的个数为( )
A.1 B.2 C.3 D.4
7.如图,在平行四边形中,的平分线交于点,的平分线交于点,若,,则的长是( )
A.2 B.1 C.3 D.3.5
8.勾股定理是几何中的一个重要定理,在我国古算书《周髀算经》中就有“若勾三,股四,则弦五”的记载.如图1是由边长相等的小正方形和直角三角形构成的,可以用其面积关系验证勾股定理.图2是由图1放入长方形内得到的, ,点D,E,F,G,H,I都在长方形的边上,则长方形的面积为( )
A.420 B.440 C.430 D.410
9.如图,正方形和正方形中,点D在上,,H是的中点,那么的长是( )
A.2.5 B. C. D.2
10.如图,在正方形中,为对角线,为上一点,过点作,与、分别交于点,,为的中点,连接,,,,下列结论中结论正确的有( )
①;②;③;④若,则,其中结论正确的有( )
A.个 B.个 C.个 D.个
二.填空题(共6小题,满分18分,每小题3分)
11.与最简二次根式是同类二次根式,则a=_____.
12.某中学随机抽查了50名学生,了解他们平均每天的睡眠时间,结果如下表所示:
时间(小时) 6 7 8 9
人数 3 6 32 9
根据学生睡眠管理相关规定﹐初中学生平均每天睡眠时间不低于8小时,该校共有学生2000人,试估计该校学生睡眠时间符合要求的约有______人.
13.如图,在五边形中,若去掉一个的角后得到一个六边形,则的度数为____________.
14.关于x的一元二次方程有一个根是0,则k的值________.
15.如图,在正方形网格中,点A、B、P是网格线的交点,则________.
16.如图,矩形的边长为4,将沿对角线翻折得到,与交于点E,再以为折痕,将进行翻折,得到.若两次折叠后,点恰好落在的边上,则的长为___________.
三.解答题(共7小题,满分52分)
17.(6分)计算:
(1); (2);
18.(6分)解方程
(1); (2); (3)
19.(8分)在正方形网格中,每个小正方形的顶点称为格点,顶点都在格点的三角形叫做格点三角形,现有A,B两个格点,请以为边分别画出符合下列要求的格点三角形.
(1)在图甲中画一个面积为4的直角三角形;
(2)在图乙中画一个等腰(非直角)三角形,且这个等腰三角形的腰长为_______________.
20.(8分)公司生产,两种型号的扫地机器人,为了解它们的扫地质量,工作人员从某月生产的,型扫地机器人中各随机抽取台,在完全相同的条件下试验,记录下它们的除尘量的数据(单位:),并进行整理,描述和分析(除尘量用表示,共分为三个等级:合格,良好,优秀),下面给出了部分信息:
台型扫地机器人的除尘量:,,,,,,,,,.
台型扫地机器人中良好等级包含的所有数据:,,,,.
抽取的,型扫地机器人除尘量统计表
型号 平均数 中位数 众数 方差 “优秀”等级所占百分比
根据以上信息,解答下列问题.
(1)填空:______,_______,_______;
(2)这个月公司生产B型扫地机器人共3000台,估计该月B型扫地机器人“优秀”等级的台数.
(3)根据以上数据,你认为该公司生产的哪种型号的扫地机器人扫地质量更好?请说明理由(写出一条理由即可).
21.(8分)世界杯是世界上级别最高的足球赛事,2023年世界杯在卡塔尔隆重举行,今年世界杯的吉样物是“拉伊卜”,它的设计灵感来源于阿拉伯标志型的白头巾,某网店现售有一大一小两种型号的“拉伊卜”摆件,已知每个大摆件的售价是每个小摆件售价的2倍还多60元,420元可购买一个大摆件和一个小摆件.
(1)每个“拉伊卜”大摆件和小摆件的售价分别是多少?
(2)第一天该网店按照原售价卖出大摆件30个,小摆件100个,因为小摆件库存量大,第二天商家调整了销售方案,大摆件的价格不变,小摆件的价格下调元,调整后,当天大摆件的销量下降了个,小摆件的销量增加了个,当天的销售额达到了20520元,求降价后的小摆件的价格.
22.(8分)在长方形中,,,点是边上的一点,将沿折叠,点的对应点为点,射线与线段交于点.
(1)如图,当点和点重合时,求证:;
(2)如图,当点正好落在矩形的对角线上时,求的长度;
(3)如图,连接,,若,求的面积.
23.(8分)中,D、E分别是,的中点,O是内任意一点,连接、.
(1)如图1,点G、F分别是、的中点,连接,,,,求证:四边形是平行四边形;
(2)如图2,若点O恰为和交点,求证:,;
(3)如图3,若点O恰为和交点,射线与交于点M,求证:.
答案
一.选择题
1.D
【分析】根据二次根式的加减乘除四则运算法则,逐项判断即可求解.
【详解】解:A、和不是同类二次根式,无法合并,故本选项错误,不符合题意;
B、,故本选项错误,不符合题意;
C、,故本选项错误,不符合题意;
D、,故本选项正确,符合题意;
故选:D
2.D
【分析】根据二次根式的性质和分式的意义,被开方数大于等于0,分母不为0,列不等式组可求得自变量的取值范围.
【详解】根据题意得:
解得:且
故选:D.
3.D
【分析】根据一组数据中出现次数最多的为众数,所有数据和除以数据的个数为平均数,最大数减最小数为极差,逐一进行判断即可.
【详解】解:A、两个数据各出现两次,众数为,选项错误,不符合题意;
B、两个数据各出现两次,众数为,选项错误,不符合题意;
C、,选项错误,不符合题意;
D、极差为:,选项正确,符合题意;
故选D.
4.A
【分析】依据一元二次方程的定义得,及一元二次方程有两个不相等实数根时,求解不等式即可.
【详解】解:依题意得,
且,
解得:且,
故选:A.
5.B
【分析】根据日历上数字规律得出,圈出的9个数,最大数与最小数的差为16,以及利用最大数与最小数的积为161,列出方程即可.
【详解】解:根据图表可以得出,圈出的9个数,最大数与最小数的差为16,设最小数为,则最大数为,
根据题意得出:,
故选:B.
6.C
【分析】根据三角形的面积和三角形面积,可以判断点可能存在线段和线段上;根据点在四边形的边上,考虑此时点存在和上,利用勾股定理和等腰三角形的性质分别求出长度和三角形的高,从而求出三角形的面积,发现与三角形面积相等,从而推出点在点处.
【详解】解:, ,
.
.
当点在边上,如图所示:
,
.
.
此时点满足条件.
当点在边上,如图所示:
,
.
.
此时点满足条件.
过点作于点,
,,
中,.
,,
.
中,
点在四边形的边上,
点和点重合,
点在点处.
满足条件的点共3个.
故答案选:.
7.A
【分析】根据平行四边形的性质证明,,进而可得和的长,然后可得答案.
【详解】解:四边形是平行四边形,
,,,
,
又平分,
,
,
,
同理可证:,
,
,
.
故选:A.
8.B
【分析】延长交于P,延长交于Q,可得全等,根据全等三角形对应边相等可得,然后求出和的长,再根据长方形的面积公式列式计算即可得解.
【详解】解:如图,延长交于P,延长交于Q,
由题意得,,
∴,
∴,
∴,
同理可证,
∴,
∵图2是由图1放入长方形内得到,
∴,,
∴长方形的面积.
故选:B.
9.B
【分析】连接,如图,根据正方形的性质得,则,再利用勾股定理计算出,然后根据直角三角形斜边上的中线求的长.
【详解】解:如图,连接,
∵正方形和正方形中,
∴,,
,
∴,
由勾股定理得,,
∵H是的中点,
∴.
故选:B.
10.D
【分析】根据正方形,为对角线,,可知四边形是矩形,由此可证、
、、是等腰直角三角形,为的中点,,可知是等腰
直角三角形,由此即可求解.
【详解】解:结论①,
∵正方形中,为对角线,,
∴,,
∴,四边形是矩形,、是等腰直角三角形,
∴,
∴,故结论①正确;
结论②,
由结论①正确可知,是等腰直角三角形,为的中点,
∴,且、是等腰直角三角形,
∴,,,
∴,且,
∴,
∴,
∵,故结论②正确;
结论③,
∵、、、是等腰直角三角形,,
∴,
∵四边形是矩形,
∴,
∴,故结论③正确;
结论④若,则,
由结论②正确,可知;由结论③正确可知,,
且、、、是等腰直角三角形,
∴,即是等腰直角三角形,
如图所示,过点作于,设,则,,,
∴,,
∴,故结论④正确;
综上所示,正确的有①②③④,
故选:.
二.填空题(共6小题,满分18分,每小题3分)
11.3
【分析】首先化简二次根式,再根据同类二次根式定义可得2a﹣3=3,再解即可.
【详解】,
∵与最简二次根式是同类二次根式,
∴2a﹣3=3,
解得:a=3,
故答案为:3.
12.人
故答案为:1640.
13.
【分析】根据多边形的内角和定理可求得,,进而可求解.
【详解】解:∵,,
∴,
∵,
∴,
故答案为:
14.2
【分析】将代入方程,结合一元二次方程,,进行求解即可.
【详解】解:∵x的一元二次方程有一个根是0,
∴,
解得:
∵,是一元二次方程,
∴,
∴,
∴;
故答案为:2.
15.45
【分析】取网格上的点C、D、E,连接.利用全等三角形的性质和平行线的性质求得,再利用勾股定理及其逆定理求得,即证明为等腰直角三角形,便可解答.
【详解】解:如图,点C、D、E是网格线交点,连接,
由图可得,
∴,
∴,
∴,
∴;
设小网格的边长为a,由勾股定理可得:,
∵,
∴
∴,
∴,
∴.
故答案为:45.
16.或
【分析】根据题意分两种情况讨论:①当点恰好落在上时,由翻折以及矩形的性质利用可证明,然后根据等腰三角形的性质求出的长,再依据勾股定理求解即可;②当点恰好落在上时,同理利用可证明,根据全等三角形的性质可得出的长,再根据线段的和差关系即可得出答案.
【详解】∵四边形为矩形,
∴,,
∵沿对角线翻折得到,
∴,,
∵以为折痕,将进行翻折,得到,
∴,,
①当点恰好落在上时,如图,
在和中,
∴
∴,即为等腰三角形,
∵
∴点为中点,
∴,
在中,有,
即,解得
②当点恰好落在上时,如图,
∵
∴四边形为矩形,
∴,
∵沿进行翻折,得到,
∴
在中,
,
在和中,
∴≌()
∴
∴.
故答案为:或.
三.解答题
17.(1)
=
=
(2)
=
=
18.(1)
,,
∴,
(2)
∴,
(3)
∴
∴,
19.(1)解:为所求作的三角形,如图所示:
(画出一种情况即可)
(2)解:为所求作的三角形,如图所示:(画出一种情况即可)
图1和图2中腰长为;
图3中腰长为.
故答案为:(画图3填).
20.(1)解:型中除尘量为的有个,数量最多,
所以众数;
型中“良好”等级包含的数据有个,则所占百分比为,
所以,即;
因为型中“合格”等级所占百分比为,
所以型中“合格”的有个,
所以型中中位数b=;
故答案为:;;;
(2)(台),
答:估计该月型扫地机器人“优秀”等级的台数有台;
(3)型号更好,
理由:在平均数均为的情况下,型号的平均除尘量众数大于型号的平均除尘量众数90.
21.(1)解:设每个小摆件的售价为x元,则每个大摆件的售价为元,根据题意得:
,
解得:,
(元),
答:每个“拉伊卜”大摆件和小摆件的售价分别是300元和120元.
(2)解:调整后,当天大摆件的销量为个,小摆件的销量为个,小摆件的价格为元,根据题意得:
,
解得:,(舍去),
(元),
答:降价后的小摆件的价格为108元.
22.(1)证明:四边形是矩形,
,
,
由折叠得:,
,
;
(2)解:四边形是矩形,
,,
,
由折叠知:,,,
,,
,
,
,
设,则,
在中,由勾股定理得,
,
,
,
;
(3)如图,作于,交于,
,
,
,
四边形是矩形,
,
四边形是矩形,
,,,
在中,,,
,
,
.
23.(1)∵D,E分别是的边,的中点,
∴是的中位线,
∴,,
同理:,,
∴,,
∴四边形是平行四边形;
(2)取,中点G,F,连接,,,,
∴,,
由(1)知,四边形是平行四边形,
∴,,
∴,;
(3)在射线上截取,连接,,
∵D,O分别是,的中点,
∴是的中位线,
∴即,
同理:,
∴四边形是平行四边形,
∴.
同课章节目录
