沪科版八年级数学下册试题 第18章 勾股定理 章节测试卷(含解析)
文档属性
| 名称 | 沪科版八年级数学下册试题 第18章 勾股定理 章节测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 228.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 15:09:57 | ||
图片预览



文档简介
第18章《勾股定理》章节测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果a:b:c=1:1:,那么△ABC是直角三角形
B.如果∠A=∠B﹣∠C,那么△ABC是直角三角形
C.如果ac,bc,那么△ABC为直角三角形
D.如果b2=a2﹣c2,那么△ABC是直角三角形且∠B=90°
2.如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,∠B=90°,∠D=α.则∠BCD的大小为( )
A.α B.90°﹣α C.45°+α D.135°﹣α
3.如图,已知钓鱼竿AC的长为10m,露在水面上的鱼线BC长为6m,某钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'为8m,则BB'的长为( )
A.1m B.2m C.3m D.4m
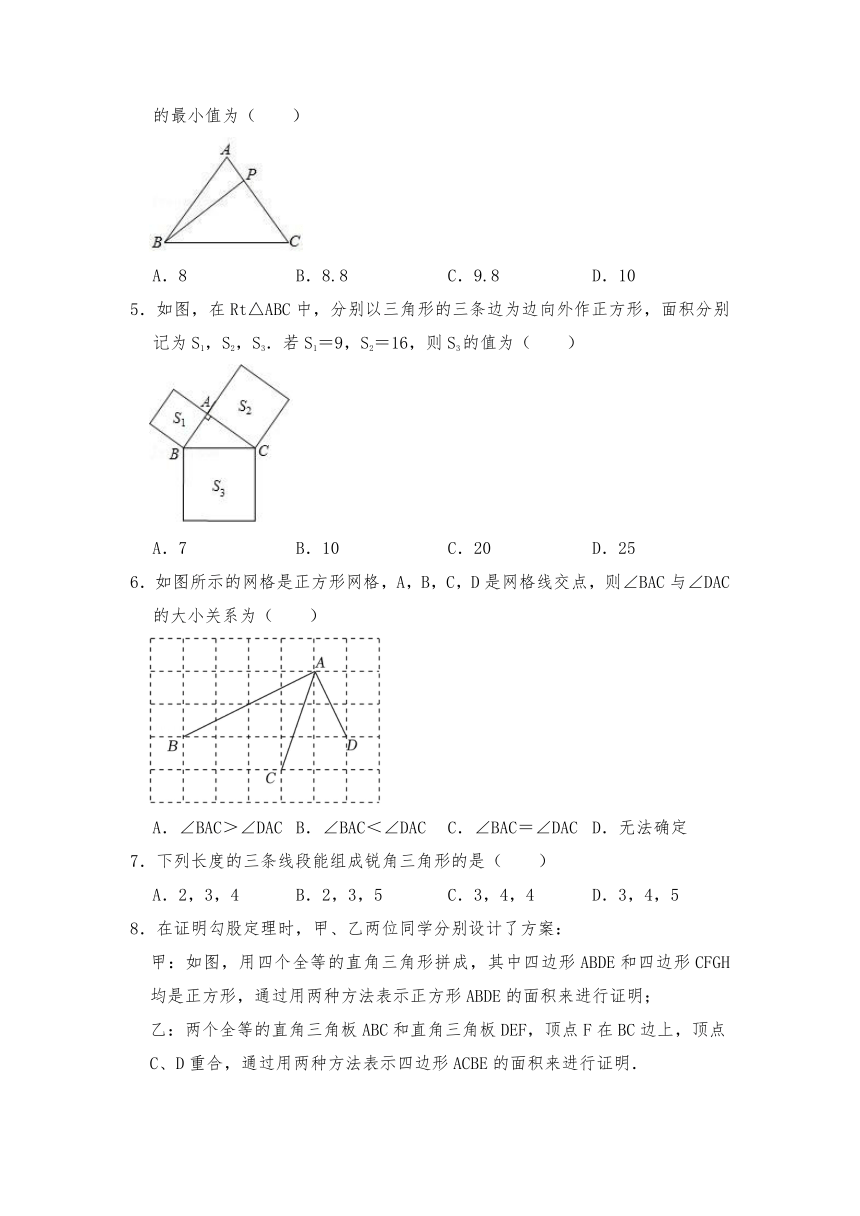
4.如图,△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
A.8 B.8.8 C.9.8 D.10
5.如图,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1=9,S2=16,则S3的值为( )
A.7 B.10 C.20 D.25
6.如图所示的网格是正方形网格,A,B,C,D是网格线交点,则∠BAC与∠DAC的大小关系为( )
A.∠BAC>∠DAC B.∠BAC<∠DAC C.∠BAC=∠DAC D.无法确定
7.下列长度的三条线段能组成锐角三角形的是( )
A.2,3,4 B.2,3,5 C.3,4,4 D.3,4,5
8.在证明勾股定理时,甲、乙两位同学分别设计了方案:
甲:如图,用四个全等的直角三角形拼成,其中四边形ABDE和四边形CFGH均是正方形,通过用两种方法表示正方形ABDE的面积来进行证明;
乙:两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,通过用两种方法表示四边形ACBE的面积来进行证明.
对于甲、乙两种方案,下列判断正确的是( )
A.甲、乙均对 B.甲对、乙不对
C.甲不对,乙对 D.甲、乙均不对
9.若一个直角三角形的两边长为4和5,则第三边长为( )
A.3 B. C.8 D.3或
10.在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
A.3 B.4 C.5 D.6
二.填空题(共6小题,满分18分,每小题3分)
11.如图,一牧童在A处放羊,牧童的家在B处,A、B距河岸的距离AC、BD分别为500m和700m,且C、D两地相距500m,天黑前牧童要将羊赶往河边喝水再回家,那么牧童至少应该走 m.
12.如图Rt△ABC中,AC=12,BC=5,分别以AB,AC,BC为直径作半圆,则图中阴影部分的面积为 .
13.观察下列一组数:
列举:3、4、5,猜想:32=4+5;
列举:5、12、13,猜想:52=12+13;
列举:7、24、25,猜想:72=24+25;
…
列举:13、b、c,猜想:132=b+c;
请你分析上述数据的规律,结合相关知识求得b= ,c= .
14.如图,设AD、BE、CF为三角形ABC的三条高,若AB=6,BC=5,AE﹣EC,则线段BE的长为 .
15.周长为24,斜边长为10的直角三角形面积为 .
16.甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是 .
三.解答题(共7小题,满分52分)
17.(6分)如图所示,已知△ABC中,CD⊥AB于D,AC=4,BC=3,DB.
(1)求CD的长;
(2)求AD的长;
(3)求证:△ABC是直角三角形.
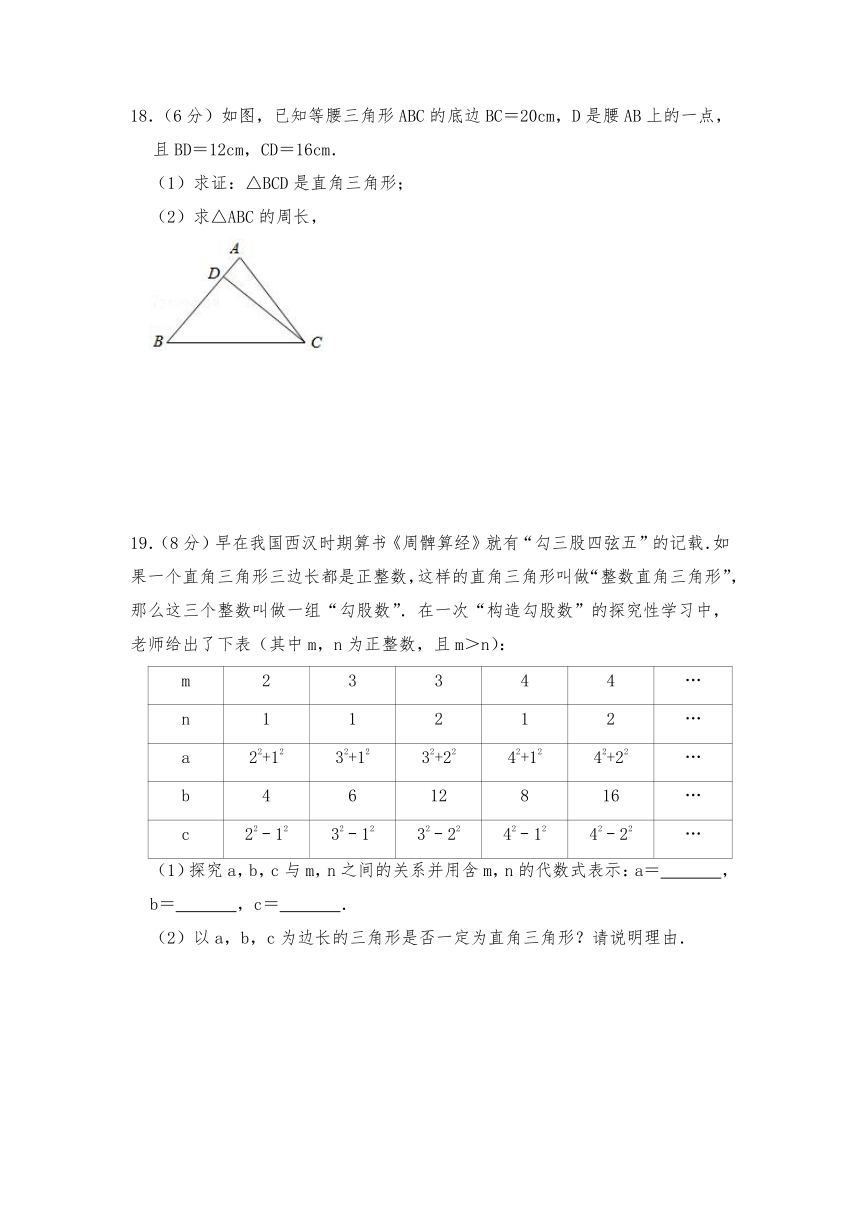
18.(6分)如图,已知等腰三角形ABC的底边BC=20cm,D是腰AB上的一点,且BD=12cm,CD=16cm.
(1)求证:△BCD是直角三角形;
(2)求△ABC的周长,
19.(8分)早在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫做“整数直角三角形”,那么这三个整数叫做一组“勾股数”.在一次“构造勾股数”的探究性学习中,老师给出了下表(其中m,n为正整数,且m>n):
m 2 3 3 4 4 …
n 1 1 2 1 2 …
a 22+12 32+12 32+22 42+12 42+22 …
b 4 6 12 8 16 …
c 22﹣12 32﹣12 32﹣22 42﹣12 42﹣22 …
(1)探究a,b,c与m,n之间的关系并用含m,n的代数式表示:a= ,b= ,c= .
(2)以a,b,c为边长的三角形是否一定为直角三角形?请说明理由.
20.(8分)阅读理解并解答问题
如果a、b、c为正整数,且满足a2+b2=c2,那么,a、b、c叫做一组勾股数.
(1)请你根据勾股数的意思,说明为什么3、4、5是一组勾股数;
(2)写出一组不同于3、4、5的勾股数;
(3)如果m表示大于1的整数,且a=2m,b=m2﹣1,c=m2+1,请你根据勾股数的意思,说明a、b、c为勾股数.
21.(8分)在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
22.(8分)如图,有一架秋千,当他静止时,踏板离地的垂直高度DE=0.6m,将他往前推送2.4m(水平距离BC=2.4m)时,秋千的踏板离地的垂直高度BF=1.2m,秋千的绳索始终拉得很直,求绳索AD的长度.
23.(8分)(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;
(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?
答案
一.选择题
1.
【分析】利用勾股定理的逆定理,三角形内角和定理,进行计算逐一判断即可解答.
【解答】解:A、∵a:b:c=1:1:,
∴设a=k,b=k,ck,
∴a2+b2=k2+k2=2k2,c2=(k)2=2k2,
∴a2+b2=c2,
∴△ABC是直角三角形,
故A不符合题意;
B、∵∠A=∠B﹣∠C,
∴∠A+∠C=∠B,
∵∠A+∠B+∠C=180°,
∴2∠B=180°,
∴∠B=90°,
∴△ABC是直角三角形,
故B不符合题意;
C、∵ac,bc,
∴a2+b2=(c)2+(c)2=c2,
∴△ABC为直角三角形,
故C不符合题意;
D、∵b2=a2﹣c2,
∴b2+c2=a2,
∴△ABC为直角三角形,
∴∠A=90°,
故D符合题意;
故选:D.
2.
【分析】由于∠B=90°,AB=BC=2,利用勾股定理可求AC,并可求∠BAC=45°,而CD=3,DA=1,易得AC2+DA2=CD2,可证△ACD是直角三角形,于是有∠CAD=90°,从而易求∠BAD,进而得出∠BCD.
【解答】解:连接AC,
∵∠B=90°,AB=BC=2,
∴AC,∠BAC=45°,
又∵CD=3,DA=1,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠DAB=45°+90°=135°,
∵∠D=α,
∴∠BCD=360°﹣90°﹣135°﹣α=135°﹣α,
故选:D.
3.
【分析】根据勾股定理分别求出AB和AB′,再根据BB′=AB﹣AB′即可得出答案.
【解答】解:∵AC=10m,BC=6m,
∴AB(m),
∵AC′=10m,B′C′=8m,
∴AB′(m),
∴BB′=AB﹣AB′=8﹣6=2(m);
故选:B.
4.
【分析】若AP+BP+CP最小,就是说当BP最小时,AP+BP+CP才最小,因为不论点P在AC上的那一点,AP+CP都等于AC.那么就需从B向AC作垂线段,交AC于P.先设AP=x,再利用勾股定理可得关于x的方程,解即可求x,在Rt△ABP中,利用勾股定理可求BP.那么AP+BP+CP的最小值可求.
【解答】解:从B向AC作垂线段BP,交AC于P,
设AP=x,则CP=5﹣x,
在Rt△ABP中,BP2=AB2﹣AP2,
在Rt△BCP中,BP2=BC2﹣CP2,
∴AB2﹣AP2=BC2﹣CP2,
∴52﹣x2=62﹣(5﹣x)2
解得x=1.4,
在Rt△ABP中,BP4.8,
∴AP+BP+CP=AC+BP=5+4.8=9.8.
故选:C.
5.
【分析】由正方形的面积公式可知S1=AB2,S2=AC2,S3=BC2,在Rt△ABC中,由勾股定理得AC2+AB2=BC2,即S1+S2=S3,由此可求S3.
【解答】解:在Rt△ABC中,AC2+AB2=BC2,
由正方形面积公式得S1=AB2,S2=AC2,S3=BC2,
∵S1=9,S2=16,
∴S3=S1+S2=9+16=25.
故选:D.
6.
【分析】连接CD,BC,设小正方形的边长为1,根据勾股定理求出AB、AC、BC、AD、CD的长,根据求出的结果得出BC=AC,AD=CD,AC2+BC2=AB2,AD2+CD2=AC2,求出△ACB和△ADC都是等腰直角三角形,再得出选项即可.
【解答】解:连接CD,BC,
设小正方形的边长为1,
由勾股定理得:AB2=22+42=4+16=20,BC2=12+32=1+9=10,AC2=12+32=1+9=10,AD2=12+22=1+4=5,CD2=12+22=1+4=5,
所以BC=AC,AD=CD,AC2+BC2=AB2,AD2+CD2=AC2,
即△ACB和△ADC都是等腰直角三角形,
所以∠BAC=∠DAC=45°,
故选:C.
7.
【分析】根据勾股定理求出以较短的两条边为直角边的三角形的斜边的长度,然后与较长的边进行比较作出判断即可.
【解答】解:A、∵4,2+3>4,∴不能组成锐角三角形;
B、∵2+3=5,∴不能组成三角形;
C、∵5>4,3+4>4,∴能组成锐角三角形;
D、∵5,是直角三角形,∴不能组成锐角三角形.
故选:C.
8.
【分析】甲:根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式;
乙:根据三角形的面积和梯形的面积公式用两种方法求得四边形ACBE的面积,于是得到结论.
【解答】甲:证明:Rt△ABC中,∠ACB=90°,设AC=b,BC=a,AB=c.
由图可知S正方形ABDE=4S△ABC+S正方形FCHG
∵S正方形ABDE=c2,S△ABCab,正方形FCHG边长为a﹣b,
∴c2=4ab+(a﹣b)2=2ab+a2﹣2ab+b2
即c2=a2+b2.故甲对;
乙:证明:∵四边形ACBE的面积=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
四边形ACBE的面积=S四边形ACFE+S△EFB(AC+EF) CFBF EF(b+a)b(a﹣b) ab2aba2aba2b2,
∴c2a2b2,
即a2+b2=c2.故乙对,
故选:A.
9.
【分析】分5是直角边、5是斜边两种情况,再由勾股定理即可得出答案.
【解答】解:当5是直角边时,则第三边为:;
当5是斜边时,则第三边为:3,
综上所述,第三边的长为3或,
故选:D.
10.
【分析】根据三个顶点都在格点上,而且三边与AB或AD都不平行,画出的形状不同的直角三角形即可.
【解答】解:如图所示:
直角边之比为1:2,如图①和②;
直角边之比为1:3,如图③
直角边之比为1:1,如图④和⑤.
形状不同的直角三角形共有3种情况.
故选:A.
二.填空题
11.
【分析】本题可以把两线段的和最小的问题转化为两点之间线段最短的问题解决.转化的方法是作A关于CD的对称点,求解对称点与B之间的距离即可.
【解答】解:作A关于CD的对称点E,连接BE,并作BF⊥AC于点F.
则EF=BD+AC=500+700=1200m,BF=CD=500m.
在Rt△BEF中,根据勾股定理得:BE1300米.
12.
【分析】利用勾股定理列式求出AB,再根据阴影部分的面积等于阴影部分所在的两个半圆的面积加上△ABC的面积减去大半圆的面积,列式计算即可得解.
【解答】解:∵AC=12,BC=5,
∴AB13,
∴阴影部分的面积π()2π()212×5π()2
ππ+30π
=30.
故答案为:30.
13.
【分析】认真观察三个数之间的关系:首先发现每一组的三个数为勾股数,第一个数为从3开始连续的奇数,第二、三个数为连续的自然数;进一步发现第一个数的平方是第二、三个数的和;最后得出第n组数为(2n+1),(),(),由此规律解决问题.
【解答】解:在32=4+5中,4,5;
在52=12+13中,12,13;
…
则在13、b、c中,b84,c85.
14.
【分析】可设AE=x,EC=y,则根据勾股定理和已知条件可得方程组,解方程组可求AE的长,再根据勾股定理可求线段BE的长.
【解答】解:设AE=x,EC=y,则
,
解得x,
则BE.
故答案为:.
15.
【分析】设直角三角形两直角边长为a,b,由周长与斜边的关系得a+b=14,中由完全平方公式和勾股定理求出ab的值,即可求出三角形的面积.
【解答】解:设直角三角形两直角边长为a,b,
∵该直角三角形的周长为24,其斜边长为10,
∴24﹣(a+b)=10,
即a+b=14,
由勾股定理得:a2+b2=102=100,
∵(a+b)2=142,
∴a2+b2+2ab=196,
即100+2ab=196,
∴ab=48,
∴直角三角形的面积ab=24,
故答案为:24.
16.
【分析】首先根据速度和时间计算出行驶路程,再根据勾股定理逆定理结合路程可判断出甲和乙两艘轮船的行驶路线呈垂直关系,进而可得答案.
【解答】解:如图:
∵甲乙两艘客轮同时离开港口,航行的速度都是每分钟40m,甲客轮用15分钟到达点A,乙客轮用20分钟到达点B,
∴甲客轮走了40×15=600(m),乙客轮走了40×20=800(m),
∵A、B两点的直线距离为1000m,
∴6002+8002=10002,
∴∠AOB=90°,
∵甲客轮沿着北偏东30°的方向航行,
∴乙客轮的航行方向可能是南偏东60°,
同理可得:乙客轮的航行方向也可能是北偏西60°.
综上所述:乙客轮的航行方向可能是南偏东60°或北偏西60°.
故答案为:南偏东60°或北偏西60°.
三.解答题
17.(1)解:在Rt△BCD中,DC;
(2)解:在Rt△CDA中
AD;
(3)证明:∵BC2=9,AC2=16,
(BD+AD)2=25,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
18.(1)证明:∵在△BDC中,BC=20cm,BD=12cm,CD=16cm.
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴△BCD是直角三角形;
(2)解:设AB=AC=xcm,则AD=(x﹣12)cm,
在Rt△ADC中,由勾股定理得:AD2+CD2=AC2,
即(x﹣12)2+162=x2,
解得:x,
即AB=ACcm,
∵BC=20cm,
∴△ABC的周长是AB+AC+BCcmcm+20cmcm.
19.解:(1)观察得,a=m2+n2,b=2mn,c=m2﹣n2.
故答案为:m2+n2,2mn,m2﹣n2;
(2)以a,b,c为边长的三角形一定为直角三角形,理由如下:
∵a2=(m2+n2)2=m4+2m2n2+n4,
b2+c2=m4﹣2m2n2+n4+4m2n2=m4+2m2n2+n4,
∴a2=b2+c2,
∴以a,b,c为边长的三角形一定为直角三角形.
20.解:(1)∵3、4、5是正整数,且32+42=52,
∴3、4、5是一组勾股数;
(2)∵122+162=202,且12,16,20都是正整数,
∴一组勾股数可以是12,16,20.答案不唯一;
(3)∵m表示大于1的整数,
∴由a=2m,b=m2﹣1,c=m2+1得到a、b、c均为正整数;
又∵a2+b2=(2m)2+(m2﹣1)2=4m2+m4﹣2m2+1=m4+2m2+1,而c2=(m2+1)2=m4+2m2+1,
∴a2+b2=c2,
∴a、b、c为勾股数.
21.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(2.4)2+(1.8)2=9
BC2=9
∴CH2+BH2=BC2
∴CH⊥AB,
所以CH是从村庄C到河边的最近路
(2)设AC=x
在Rt△ACH中,由已知得AC=x,AH=x﹣1.8,CH=2.4
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣1.8)2+(2.4)2
解这个方程,得x=2.5,
答:原来的路线AC的长为2.5千米.
22.解:在Rt△ACB中,
AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x+0.6﹣1.2)m,
故x2=2.42+(x+0.6﹣1.2)2,5.76﹣1.2x+0.36=0
解得:x=5.1,
答:绳索AD的长度是5.1m.
23.解:(1)由题意得:该长方体中能放入木棒的最大长度是:
(cm).
(2)分三种情况可得:AGcm>AGcm>AGcm,
所以最短路程为cm;
(3)∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,
此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,
∴A′D=5cm,BD=12﹣3+AE=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B13(cm)
一.选择题(共10小题,满分30分,每小题3分)
1.在△ABC中,∠A,∠B,∠C的对边分别记为a,b,c,下列结论中不正确的是( )
A.如果a:b:c=1:1:,那么△ABC是直角三角形
B.如果∠A=∠B﹣∠C,那么△ABC是直角三角形
C.如果ac,bc,那么△ABC为直角三角形
D.如果b2=a2﹣c2,那么△ABC是直角三角形且∠B=90°
2.如图,在四边形ABCD中,AB=BC=2,CD=3,AD=1,∠B=90°,∠D=α.则∠BCD的大小为( )
A.α B.90°﹣α C.45°+α D.135°﹣α
3.如图,已知钓鱼竿AC的长为10m,露在水面上的鱼线BC长为6m,某钓鱼者想看看鱼钩上的情况,把鱼竿AC转动到AC'的位置,此时露在水面上的鱼线B'C'为8m,则BB'的长为( )
A.1m B.2m C.3m D.4m
4.如图,△ABC中,有一点P在AC上移动.若AB=AC=5,BC=6,则AP+BP+CP的最小值为( )
A.8 B.8.8 C.9.8 D.10
5.如图,在Rt△ABC中,分别以三角形的三条边为边向外作正方形,面积分别记为S1,S2,S3.若S1=9,S2=16,则S3的值为( )
A.7 B.10 C.20 D.25
6.如图所示的网格是正方形网格,A,B,C,D是网格线交点,则∠BAC与∠DAC的大小关系为( )
A.∠BAC>∠DAC B.∠BAC<∠DAC C.∠BAC=∠DAC D.无法确定
7.下列长度的三条线段能组成锐角三角形的是( )
A.2,3,4 B.2,3,5 C.3,4,4 D.3,4,5
8.在证明勾股定理时,甲、乙两位同学分别设计了方案:
甲:如图,用四个全等的直角三角形拼成,其中四边形ABDE和四边形CFGH均是正方形,通过用两种方法表示正方形ABDE的面积来进行证明;
乙:两个全等的直角三角板ABC和直角三角板DEF,顶点F在BC边上,顶点C、D重合,通过用两种方法表示四边形ACBE的面积来进行证明.
对于甲、乙两种方案,下列判断正确的是( )
A.甲、乙均对 B.甲对、乙不对
C.甲不对,乙对 D.甲、乙均不对
9.若一个直角三角形的两边长为4和5,则第三边长为( )
A.3 B. C.8 D.3或
10.在数学活动课上,老师要求学生在4×4的正方形ABCD网格中(小正方形的边长为1)画直角三角形,要求三个顶点都在格点上,而且三边与AB或AD都不平行,则画出的形状不同的直角三角形有( )种.
A.3 B.4 C.5 D.6
二.填空题(共6小题,满分18分,每小题3分)
11.如图,一牧童在A处放羊,牧童的家在B处,A、B距河岸的距离AC、BD分别为500m和700m,且C、D两地相距500m,天黑前牧童要将羊赶往河边喝水再回家,那么牧童至少应该走 m.
12.如图Rt△ABC中,AC=12,BC=5,分别以AB,AC,BC为直径作半圆,则图中阴影部分的面积为 .
13.观察下列一组数:
列举:3、4、5,猜想:32=4+5;
列举:5、12、13,猜想:52=12+13;
列举:7、24、25,猜想:72=24+25;
…
列举:13、b、c,猜想:132=b+c;
请你分析上述数据的规律,结合相关知识求得b= ,c= .
14.如图,设AD、BE、CF为三角形ABC的三条高,若AB=6,BC=5,AE﹣EC,则线段BE的长为 .
15.周长为24,斜边长为10的直角三角形面积为 .
16.甲、乙两艘客轮同时离开港口,航行的速度都是40m/min,甲客轮用15min到达点A,乙客轮用20min到达点B.若A,B两点的直线距离为1000m,甲客轮沿着北偏东30°的方向航行,则乙客轮的航行方向可能是 .
三.解答题(共7小题,满分52分)
17.(6分)如图所示,已知△ABC中,CD⊥AB于D,AC=4,BC=3,DB.
(1)求CD的长;
(2)求AD的长;
(3)求证:△ABC是直角三角形.
18.(6分)如图,已知等腰三角形ABC的底边BC=20cm,D是腰AB上的一点,且BD=12cm,CD=16cm.
(1)求证:△BCD是直角三角形;
(2)求△ABC的周长,
19.(8分)早在我国西汉时期算书《周髀算经》就有“勾三股四弦五”的记载.如果一个直角三角形三边长都是正整数,这样的直角三角形叫做“整数直角三角形”,那么这三个整数叫做一组“勾股数”.在一次“构造勾股数”的探究性学习中,老师给出了下表(其中m,n为正整数,且m>n):
m 2 3 3 4 4 …
n 1 1 2 1 2 …
a 22+12 32+12 32+22 42+12 42+22 …
b 4 6 12 8 16 …
c 22﹣12 32﹣12 32﹣22 42﹣12 42﹣22 …
(1)探究a,b,c与m,n之间的关系并用含m,n的代数式表示:a= ,b= ,c= .
(2)以a,b,c为边长的三角形是否一定为直角三角形?请说明理由.
20.(8分)阅读理解并解答问题
如果a、b、c为正整数,且满足a2+b2=c2,那么,a、b、c叫做一组勾股数.
(1)请你根据勾股数的意思,说明为什么3、4、5是一组勾股数;
(2)写出一组不同于3、4、5的勾股数;
(3)如果m表示大于1的整数,且a=2m,b=m2﹣1,c=m2+1,请你根据勾股数的意思,说明a、b、c为勾股数.
21.(8分)在一条东西走向河的一侧有一村庄C,河边原有两个取水点A,B,其中AB=AC,由于某种原因,由C到A的路现在已经不通,某村为方便村民取水决定在河边新建一个取水点H(A、H、B在一条直线上),并新修一条路CH,测得CB=3千米,CH=2.4千米,HB=1.8千米.
(1)问CH是否为从村庄C到河边的最近路?(即问:CH与AB是否垂直?)请通过计算加以说明;
(2)求原来的路线AC的长.
22.(8分)如图,有一架秋千,当他静止时,踏板离地的垂直高度DE=0.6m,将他往前推送2.4m(水平距离BC=2.4m)时,秋千的踏板离地的垂直高度BF=1.2m,秋千的绳索始终拉得很直,求绳索AD的长度.
23.(8分)(1)如图1,长方体的长为4cm,宽为3cm,高为12cm.求该长方体中能放入木棒的最大长度;
(2)如图2,长方体的长为4cm,宽为3cm,高为12cm.现有一只蚂蚁从点A处沿长方体的表面爬到点G处,求它爬行的最短路程.
(3)若将题中的长方体换成透明圆柱形容器(容器厚度忽略不计)的高为12cm,底面周长为10cm,在容器内壁离底部3cm的点B处有一饭粒,此时一只蚂蚁正好在容器外壁且离容器上沿3cm的点A处.求蚂蚁吃到饭粒需要爬行的最短路程是多少?
答案
一.选择题
1.
【分析】利用勾股定理的逆定理,三角形内角和定理,进行计算逐一判断即可解答.
【解答】解:A、∵a:b:c=1:1:,
∴设a=k,b=k,ck,
∴a2+b2=k2+k2=2k2,c2=(k)2=2k2,
∴a2+b2=c2,
∴△ABC是直角三角形,
故A不符合题意;
B、∵∠A=∠B﹣∠C,
∴∠A+∠C=∠B,
∵∠A+∠B+∠C=180°,
∴2∠B=180°,
∴∠B=90°,
∴△ABC是直角三角形,
故B不符合题意;
C、∵ac,bc,
∴a2+b2=(c)2+(c)2=c2,
∴△ABC为直角三角形,
故C不符合题意;
D、∵b2=a2﹣c2,
∴b2+c2=a2,
∴△ABC为直角三角形,
∴∠A=90°,
故D符合题意;
故选:D.
2.
【分析】由于∠B=90°,AB=BC=2,利用勾股定理可求AC,并可求∠BAC=45°,而CD=3,DA=1,易得AC2+DA2=CD2,可证△ACD是直角三角形,于是有∠CAD=90°,从而易求∠BAD,进而得出∠BCD.
【解答】解:连接AC,
∵∠B=90°,AB=BC=2,
∴AC,∠BAC=45°,
又∵CD=3,DA=1,
∴AC2+DA2=8+1=9,CD2=9,
∴AC2+DA2=CD2,
∴△ACD是直角三角形,
∴∠CAD=90°,
∴∠DAB=45°+90°=135°,
∵∠D=α,
∴∠BCD=360°﹣90°﹣135°﹣α=135°﹣α,
故选:D.
3.
【分析】根据勾股定理分别求出AB和AB′,再根据BB′=AB﹣AB′即可得出答案.
【解答】解:∵AC=10m,BC=6m,
∴AB(m),
∵AC′=10m,B′C′=8m,
∴AB′(m),
∴BB′=AB﹣AB′=8﹣6=2(m);
故选:B.
4.
【分析】若AP+BP+CP最小,就是说当BP最小时,AP+BP+CP才最小,因为不论点P在AC上的那一点,AP+CP都等于AC.那么就需从B向AC作垂线段,交AC于P.先设AP=x,再利用勾股定理可得关于x的方程,解即可求x,在Rt△ABP中,利用勾股定理可求BP.那么AP+BP+CP的最小值可求.
【解答】解:从B向AC作垂线段BP,交AC于P,
设AP=x,则CP=5﹣x,
在Rt△ABP中,BP2=AB2﹣AP2,
在Rt△BCP中,BP2=BC2﹣CP2,
∴AB2﹣AP2=BC2﹣CP2,
∴52﹣x2=62﹣(5﹣x)2
解得x=1.4,
在Rt△ABP中,BP4.8,
∴AP+BP+CP=AC+BP=5+4.8=9.8.
故选:C.
5.
【分析】由正方形的面积公式可知S1=AB2,S2=AC2,S3=BC2,在Rt△ABC中,由勾股定理得AC2+AB2=BC2,即S1+S2=S3,由此可求S3.
【解答】解:在Rt△ABC中,AC2+AB2=BC2,
由正方形面积公式得S1=AB2,S2=AC2,S3=BC2,
∵S1=9,S2=16,
∴S3=S1+S2=9+16=25.
故选:D.
6.
【分析】连接CD,BC,设小正方形的边长为1,根据勾股定理求出AB、AC、BC、AD、CD的长,根据求出的结果得出BC=AC,AD=CD,AC2+BC2=AB2,AD2+CD2=AC2,求出△ACB和△ADC都是等腰直角三角形,再得出选项即可.
【解答】解:连接CD,BC,
设小正方形的边长为1,
由勾股定理得:AB2=22+42=4+16=20,BC2=12+32=1+9=10,AC2=12+32=1+9=10,AD2=12+22=1+4=5,CD2=12+22=1+4=5,
所以BC=AC,AD=CD,AC2+BC2=AB2,AD2+CD2=AC2,
即△ACB和△ADC都是等腰直角三角形,
所以∠BAC=∠DAC=45°,
故选:C.
7.
【分析】根据勾股定理求出以较短的两条边为直角边的三角形的斜边的长度,然后与较长的边进行比较作出判断即可.
【解答】解:A、∵4,2+3>4,∴不能组成锐角三角形;
B、∵2+3=5,∴不能组成三角形;
C、∵5>4,3+4>4,∴能组成锐角三角形;
D、∵5,是直角三角形,∴不能组成锐角三角形.
故选:C.
8.
【分析】甲:根据题意,我们可在图中找等量关系,由中间的小正方形的面积等于大正方形的面积减去四个直角三角形的面积,列出等式化简即可得出勾股定理的表达式;
乙:根据三角形的面积和梯形的面积公式用两种方法求得四边形ACBE的面积,于是得到结论.
【解答】甲:证明:Rt△ABC中,∠ACB=90°,设AC=b,BC=a,AB=c.
由图可知S正方形ABDE=4S△ABC+S正方形FCHG
∵S正方形ABDE=c2,S△ABCab,正方形FCHG边长为a﹣b,
∴c2=4ab+(a﹣b)2=2ab+a2﹣2ab+b2
即c2=a2+b2.故甲对;
乙:证明:∵四边形ACBE的面积=S△ACB+S△ABEAB DGAB EGAB (DG+EG)AB DEc2,
四边形ACBE的面积=S四边形ACFE+S△EFB(AC+EF) CFBF EF(b+a)b(a﹣b) ab2aba2aba2b2,
∴c2a2b2,
即a2+b2=c2.故乙对,
故选:A.
9.
【分析】分5是直角边、5是斜边两种情况,再由勾股定理即可得出答案.
【解答】解:当5是直角边时,则第三边为:;
当5是斜边时,则第三边为:3,
综上所述,第三边的长为3或,
故选:D.
10.
【分析】根据三个顶点都在格点上,而且三边与AB或AD都不平行,画出的形状不同的直角三角形即可.
【解答】解:如图所示:
直角边之比为1:2,如图①和②;
直角边之比为1:3,如图③
直角边之比为1:1,如图④和⑤.
形状不同的直角三角形共有3种情况.
故选:A.
二.填空题
11.
【分析】本题可以把两线段的和最小的问题转化为两点之间线段最短的问题解决.转化的方法是作A关于CD的对称点,求解对称点与B之间的距离即可.
【解答】解:作A关于CD的对称点E,连接BE,并作BF⊥AC于点F.
则EF=BD+AC=500+700=1200m,BF=CD=500m.
在Rt△BEF中,根据勾股定理得:BE1300米.
12.
【分析】利用勾股定理列式求出AB,再根据阴影部分的面积等于阴影部分所在的两个半圆的面积加上△ABC的面积减去大半圆的面积,列式计算即可得解.
【解答】解:∵AC=12,BC=5,
∴AB13,
∴阴影部分的面积π()2π()212×5π()2
ππ+30π
=30.
故答案为:30.
13.
【分析】认真观察三个数之间的关系:首先发现每一组的三个数为勾股数,第一个数为从3开始连续的奇数,第二、三个数为连续的自然数;进一步发现第一个数的平方是第二、三个数的和;最后得出第n组数为(2n+1),(),(),由此规律解决问题.
【解答】解:在32=4+5中,4,5;
在52=12+13中,12,13;
…
则在13、b、c中,b84,c85.
14.
【分析】可设AE=x,EC=y,则根据勾股定理和已知条件可得方程组,解方程组可求AE的长,再根据勾股定理可求线段BE的长.
【解答】解:设AE=x,EC=y,则
,
解得x,
则BE.
故答案为:.
15.
【分析】设直角三角形两直角边长为a,b,由周长与斜边的关系得a+b=14,中由完全平方公式和勾股定理求出ab的值,即可求出三角形的面积.
【解答】解:设直角三角形两直角边长为a,b,
∵该直角三角形的周长为24,其斜边长为10,
∴24﹣(a+b)=10,
即a+b=14,
由勾股定理得:a2+b2=102=100,
∵(a+b)2=142,
∴a2+b2+2ab=196,
即100+2ab=196,
∴ab=48,
∴直角三角形的面积ab=24,
故答案为:24.
16.
【分析】首先根据速度和时间计算出行驶路程,再根据勾股定理逆定理结合路程可判断出甲和乙两艘轮船的行驶路线呈垂直关系,进而可得答案.
【解答】解:如图:
∵甲乙两艘客轮同时离开港口,航行的速度都是每分钟40m,甲客轮用15分钟到达点A,乙客轮用20分钟到达点B,
∴甲客轮走了40×15=600(m),乙客轮走了40×20=800(m),
∵A、B两点的直线距离为1000m,
∴6002+8002=10002,
∴∠AOB=90°,
∵甲客轮沿着北偏东30°的方向航行,
∴乙客轮的航行方向可能是南偏东60°,
同理可得:乙客轮的航行方向也可能是北偏西60°.
综上所述:乙客轮的航行方向可能是南偏东60°或北偏西60°.
故答案为:南偏东60°或北偏西60°.
三.解答题
17.(1)解:在Rt△BCD中,DC;
(2)解:在Rt△CDA中
AD;
(3)证明:∵BC2=9,AC2=16,
(BD+AD)2=25,
∴BC2+AC2=AB2,
∴△ABC是直角三角形.
18.(1)证明:∵在△BDC中,BC=20cm,BD=12cm,CD=16cm.
∴BD2+CD2=BC2,
∴∠BDC=90°,
∴△BCD是直角三角形;
(2)解:设AB=AC=xcm,则AD=(x﹣12)cm,
在Rt△ADC中,由勾股定理得:AD2+CD2=AC2,
即(x﹣12)2+162=x2,
解得:x,
即AB=ACcm,
∵BC=20cm,
∴△ABC的周长是AB+AC+BCcmcm+20cmcm.
19.解:(1)观察得,a=m2+n2,b=2mn,c=m2﹣n2.
故答案为:m2+n2,2mn,m2﹣n2;
(2)以a,b,c为边长的三角形一定为直角三角形,理由如下:
∵a2=(m2+n2)2=m4+2m2n2+n4,
b2+c2=m4﹣2m2n2+n4+4m2n2=m4+2m2n2+n4,
∴a2=b2+c2,
∴以a,b,c为边长的三角形一定为直角三角形.
20.解:(1)∵3、4、5是正整数,且32+42=52,
∴3、4、5是一组勾股数;
(2)∵122+162=202,且12,16,20都是正整数,
∴一组勾股数可以是12,16,20.答案不唯一;
(3)∵m表示大于1的整数,
∴由a=2m,b=m2﹣1,c=m2+1得到a、b、c均为正整数;
又∵a2+b2=(2m)2+(m2﹣1)2=4m2+m4﹣2m2+1=m4+2m2+1,而c2=(m2+1)2=m4+2m2+1,
∴a2+b2=c2,
∴a、b、c为勾股数.
21.解:(1)是,
理由是:在△CHB中,
∵CH2+BH2=(2.4)2+(1.8)2=9
BC2=9
∴CH2+BH2=BC2
∴CH⊥AB,
所以CH是从村庄C到河边的最近路
(2)设AC=x
在Rt△ACH中,由已知得AC=x,AH=x﹣1.8,CH=2.4
由勾股定理得:AC2=AH2+CH2
∴x2=(x﹣1.8)2+(2.4)2
解这个方程,得x=2.5,
答:原来的路线AC的长为2.5千米.
22.解:在Rt△ACB中,
AC2+BC2=AB2,
设秋千的绳索长为xm,则AC=(x+0.6﹣1.2)m,
故x2=2.42+(x+0.6﹣1.2)2,5.76﹣1.2x+0.36=0
解得:x=5.1,
答:绳索AD的长度是5.1m.
23.解:(1)由题意得:该长方体中能放入木棒的最大长度是:
(cm).
(2)分三种情况可得:AGcm>AGcm>AGcm,
所以最短路程为cm;
(3)∵高为12cm,底面周长为10cm,在容器内壁离容器底部3cm的点B处有一饭粒,
此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点A处,
∴A′D=5cm,BD=12﹣3+AE=12cm,
∴将容器侧面展开,作A关于EF的对称点A′,
连接A′B,则A′B即为最短距离,
A′B13(cm)
