沪科版八年级数学下册试题 期中检测卷(含解析)
文档属性
| 名称 | 沪科版八年级数学下册试题 期中检测卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 403.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 15:11:02 | ||
图片预览



文档简介
期中检测卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列二次根式中是最简二次根式的是( )
A. B. C. D.
2.实数a,b在数轴上的位置如图所示,则化简的结果是( )
A. B. C. D.0
3.一元二次方程有一个正根和一个负根,则a的取值范围是( )
A. B. C. D.
4.已知是整数,则正整数n的最小值为( )
A.2 B.3 C.4 D.5
5.等腰三角形的三边长分别为,,1,且关于的一元二次方程的两个根是和,则的值为( )
A.1 B.1或2 C.2 D.1且2
6.对于一元二次方程,下列说法:
①若,则;
②若方程有两个不相等的实根,则方程必有两个不相等的实根;
③若c是方程的一个根,则一定有成立;
②若是一元二次方程的根,则其中正确的( )
A.只有①②④ B.只有①②③ C.①②③④ D.只有①②
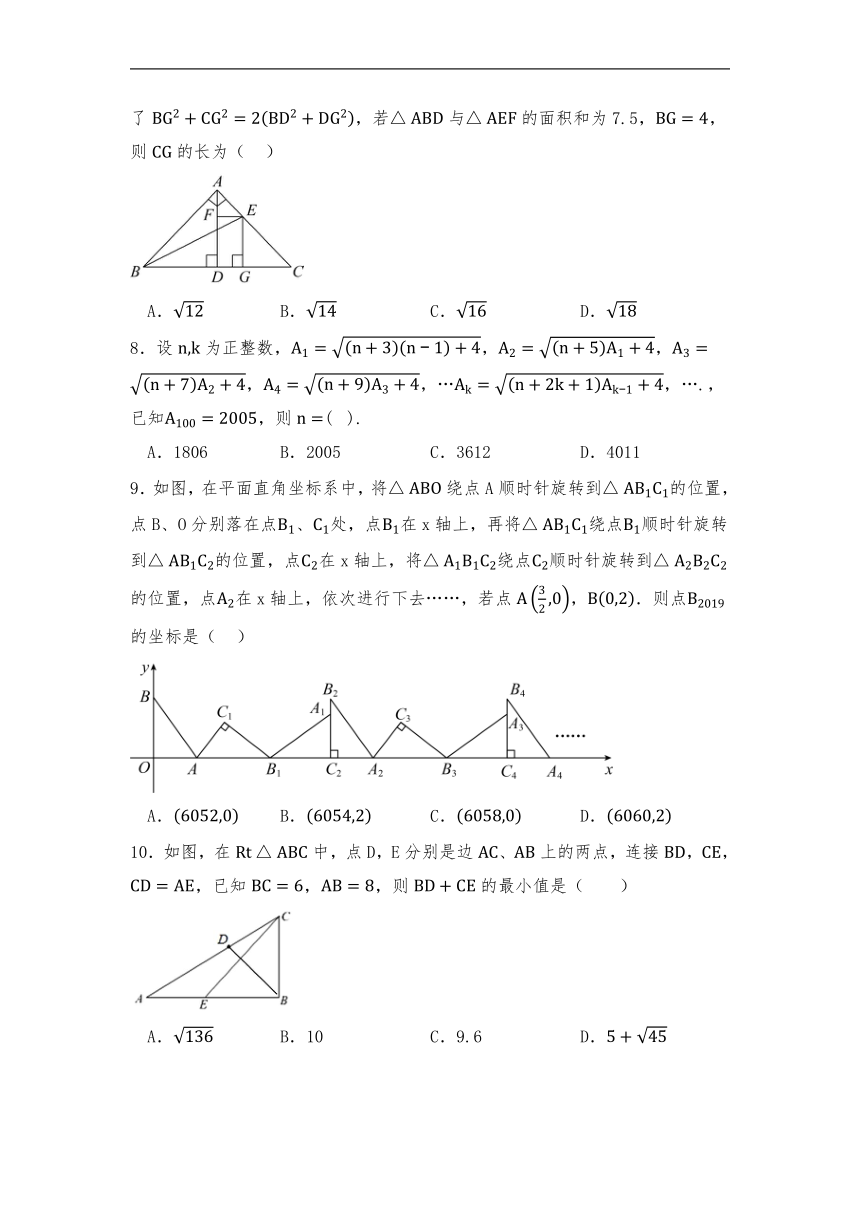
7.如图,在等腰直角中,,是的高线,E是边上一点,分别作于点F,于点G,几何原本中曾用该图证明了,若与的面积和为7.5,,则的长为( )
A. B. C. D.
8.设为正整数,,,,,…,….,已知,则( ).
A.1806 B.2005 C.3612 D.4011
9.如图,在平面直角坐标系中,将绕点A顺时针旋转到的位置,点B、O分别落在点、处,点在x轴上,再将绕点顺时针旋转到的位置,点在x轴上,将绕点顺时针旋转到的位置,点在x轴上,依次进行下去……,若点,.则点的坐标是( )
A. B. C. D.
10.如图,在中,点D,E分别是边、上的两点,连接,,,已知,,则的最小值是( )
A. B.10 C.9.6 D.
二.填空题(共6小题,满分18分,每小题3分)
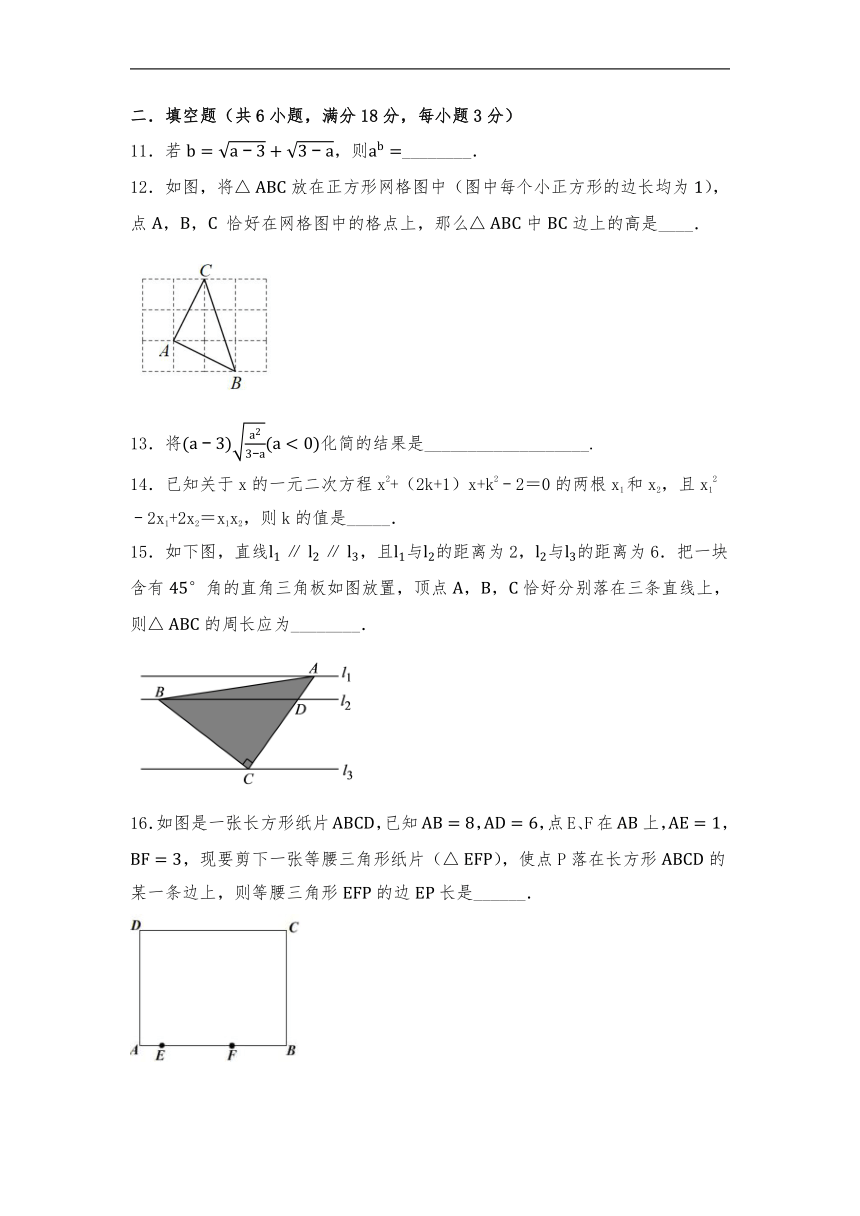
11.若,则________.
12.如图,将放在正方形网格图中(图中每个小正方形的边长均为),点,, 恰好在网格图中的格点上,那么中边上的高是____.
13.将化简的结果是___________________.
14.已知关于x的一元二次方程x2+(2k+1)x+k2﹣2=0的两根x1和x2,且x12﹣2x1+2x2=x1x2,则k的值是_____.
15.如下图,直线,且与的距离为2,与的距离为6.把一块含有角的直角三角板如图放置,顶点,,恰好分别落在三条直线上,则的周长应为________.
16.如图是一张长方形纸片,已知,,点E、F在上,,,现要剪下一张等腰三角形纸片(),使点P落在长方形的某一条边上,则等腰三角形的边长是______.
三.解答题(共7小题,满分52分)
17.(6分)计算:
(1); (2).
18.(6分)解下列方程:
(1)(用配方法) (2)(用公式法)
(3) (4)
19.如图,已知四边形中,平分,,与互补,求证:.
20.(8分)关于的一元二次方程.
(1)求证:无论取任何实数,此方程总有两个不相等的实数根
(2)设该方程两个同号的实数根为,,试问是否存在使成立,若存在,求出的值,若不存在,请说明理由.
21.(8分)年9月,新冠病毒再次席卷贵阳,戴口罩是阻断病毒传播的重要措施之一,某商家对一款成本价为每盒元医用口罩进行销售,如果按每盒元销售,每天可卖出盒,通过市场调查发现,每盒口罩售价每降低1元,则日销售量增加2盒.
(1)若每盒售价降低x元,则日销售量可表示为 盒,每盒口罩的利润为 元.
(2)若日利润保持不变,商家想尽快销售完该款口罩,每盒售价应定为多少元?
22.(8分)请阅读下列材料:
形如的式子的化简,我们只要找到两个正数a,b,使,即,那么便有.
例如:化简.
解:首先把化为,这里,
由于,即,
所以.
请根据材料解答下列问题:
(1)填空:__________.
(2)化简:(请写出计算过程).
23.(8分)如图1,直角三角形和直角三角形的直角顶点重合,点在斜边上,,,连接AE.
(1)求证:.
(2)若,求的长.
(3)如图2,点也在边上,且在点A,D之间,若,求证:.
答案
一.选择题
1.B
【分析】根据最简二次根式的定义,即可进行解答.
【详解】解:A、不是最简二次根式,故A不符合题意;
B、是最简二次根式,故B符合题意;
C、不是最简二次根式,故C不符合题意;
D、不是最简二次根式,故D不符合题意;
故选:B.
2.A
【分析】先根据数轴判断出a、b和a-b的符号,然后根据二次根式的性质化简求值即可.
【详解】解:由数轴可知:a<0,b>0,a-b<0
∴
=
=-a-b+a-b
=
故选A.
3.A
【分析】设一元二次方程的两个根为,根据题意,求解即可.
【详解】设一元二次方程的两个根为,
根据题意,
∴解得.
故选A.
4.A
【分析】根据是整数,,推出是完全平方数,设,得到,根据与同奇同偶,,,或,,得到,或,推出n的最小正整数值是2.
【详解】∵是整数,且,
∴是完全平方数,
设(m是正整数),
则,
∵与同奇同偶,
∴,或,
∴,或,
∴,
∴n的最小正整数值是2.
故选:A.
5.C
【分析】分1为底边长或腰长两种情况考虑:当1为底时,由及即可求出、的值,利用三角形的三边关系确定此种情况存在,再利用根与系数的关系找出即可;当1为腰时,则、中有一个为1,则另一个为3,由1、1、3不能围成三角形可排除此种情况.综上即可得出结论.
【详解】解:当1为底边长时,则,,
.
,2,2能围成三角形,
,
解得:;
当1为腰长时,、中有一个为1,则另一个为3,
,1,3不能围成三角形,
此种情况不存在.
故选:C.
6.A
【分析】根据一元二次方程的根、一元二次方程的根的判别式、等式的性质解决此题.
【详解】①当x=1时,a×12+b×1+c=a+b+c=0,那么一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根或有两个相等的实数根,此时b2-4ac≥0成立,那么①一定正确.
②方程ax2+c=0有两个不相等的实根,则-4ac>0,那么b2-4ac>0,故方程ax2+bx+c=0(a≠0)必有两个不相等的实根,进而推断出②正确.
③由c是方程ax2+bx+c=0的一个根,得ac2+bc+c=0.当c≠0,则ac+b+1=0;当c=0,则ac+b+1不一定等于0,那么③不一定正确.
④(2ax0+b)2=4a2x02+b2+4abx0,由b2-4ac=4a2x02+b2+4abx0,得ax02+bx0+c=0.由x0是一元二次方程ax2+bx+c=0的根,则ax02+bx0+c=0成立,那么④正确.
综上:正确的有①②④,共3个.
故选:A.
7.B
【分析】由,得,从而有,即可得出答案.
【详解】由题意知:与都是等腰直三角形,
,
∵,
∴,
∵,
∴,
∵,
∴,
故选:B
8.A
【分析】利用多项式的乘法把各数开方进行计算,然后求出A1,A2,A3的值,从而找出规律并写出规律表达式,再把k=100代入进行计算即可求解.
【详解】∵(n+3)(n-1)+4=n2+2n-3+4=n2+2n+1=(n+1)2,
∴A1=
∵(n+5)A1+4=(n+5)(n+1)+4=n2+6n+5+4=n2+6n+9=(n+3)2,
∴A2=
∵(n+7)A2+4=(n+7)(n+3)+4=n2+10n+21+4=n2+10n+25=(n+5)2,
∴A3=
依此类推,Ak=n+(2k-1)
∴A100=n+(2×100-1)=2005
解得,n=1806.
故选A.
9.C
【分析】首先根据已知求出三角形三边长度,然后通过旋转发现,…,由图象可知点在x轴上,,根据这个规律可以求得的坐标.
【详解】解:由图象可知点在x轴上,
,
,
,
,
,
.
故选C.
10.A
【分析】过点A作,并使得,连接,构造,然后得到,进而得知,连接,即可得知的长度即为的最小值,也就是的最小值,最后利用勾股定理求得的值即可得到答案.
【详解】解:如图,过点A作,并使得,连接,则,
∴,
∵在中,,
∴,
∵,,
∴,
∴,
∴,
连接,即可得知的长度即为的最小值,也就是的最小值,
∵,,,
∴,
∵,
∴,
∴的最小值是,故A正确.
故选:A.
二.填空题
11.1
【分析】根据二次根式的性质,求得,,即可求解.
【详解】解:由二次根式的性质可得,,,
解得,
则,
∴,
故答案为:1.
12.
【分析】根据所给出的图形求出的长以及的度数,再根据三角形的面积公式列出方程进行计算即可.
【详解】解:根据图形可得:,,
∴,
∴是直角三角形,且,
设中的高是x,
则,
∴,
解得,
故答案为:.
13..
【分析】根据二次根式的性质化简即可.
【详解】∵a<0.∴a-3<0,∴==.
故答案为.
14.-2或
【分析】先由x12-2x1+2x2=x1x2,得出x1-2=0或x1-x2=0,再分两种情况进行讨论:①如果x1-2=0,将x=2代入x2+(2k+1)x+k2-2=0,得4+2(2k+1)+k2-2=0,解方程求出k=-2;②如果x1-x2=0,那么△=0,解方程即可求解.
【详解】∵x12-2x1+2x2=x1x2,
x12-2x1+2x2-x1x2=0,
x1(x1-2)-x2(x1-2)=0,
(x1-2)(x1-x2)=0,
∴x1-2=0或x1-x2=0.
①如果x1-2=0,那么x1=2,
将x=2代入x2+(2k+1)x+k2-2=0,
得4+2(2k+1)+k2-2=0,
整理,得k2+4k+4=0,
解得k=-2;
②如果x1-x2=0,
则△=(2k+1)2-4(k2-2)=0.
解得: ,
∴k的值为-2或.
故答案为:-2或.
15.
【分析】作⊥于,作于,得出,,再证明,得出,,根据勾股定理求出,,即可得出结果.
【详解】解:作⊥于,作于,如图,
则,,,
∴,
由题意可知,是等腰直角三角形,
∴,,
∴,
∴,
在和中,,
∴,
∴,
∴,
∴,
则,
∴的周长为:.
故答案为:.
16.或或
【分析】分三种情况当,是等腰三角形时,当,是等腰三角形时,当,是等腰三角形时,利用等腰三角形的性质与勾股定理求解即可.
【详解】解:∵,,,
∴,
如图所示,当,是等腰三角形时,则;
如图所示,当,是等腰三角形时,则;
在中,由勾股定理得,
在中,由勾股定理得;
如图所示,当,是等腰三角形时,过点作于H,则四边形是矩形,
∴,
∴,
在中,由勾股定理得
综上所述,长是或或,
故答案为:或或.
三.解答题
17.(1)解:原式
;
(2)解:原式
.
18.(1)解:,
移项得:,
配方得:,
即:,
开平方得:,
解得:,.
(2)解:,
,
∴,
解得:,.
(3)解:,
将一元二次方程化为一般形式为:,
分解因式得:,
∴或,
解得:,.
(4)解:,
将一元二次方程化为一般形式为:,
分解因式得:,
∴或,
解得:,.
19.证明:过C点分别作的垂线,垂足分别为E、F,
∵为的平分线,,
∴.
而与互补,与也互补,
∴.
在与中,,
∴.
∴.
∵为的平分线,,
∴,
∴,
∵,
∴,
∴.
20.(1)证明:,
无论取任何实数,此方程总有两个不相等的实数根.
(2)由根与系数的关系可得:,,
,
则有,
,
整理得:,
解得:或,
由方程有两个同号的实数根可得:,即m-2>0,
m>2,
不存在m使成立.
21.(1)解:由题意可得,
∵每盒口罩售价每降低1元,则日销售量增加2盒,
∴若每盒售价降低x元,则日销售量为,
利润为:(元)
故答案为:,;
(2)解:由题意可得,
,
解得:,,
∵商家想尽快销售完该款口罩,
∴,
即售价为:(元),
答:每盒售价应定为元.
22.(1)解:,
故答案为:;
(2)解:由可得,这里,
∵,即,
∴.
23.(1)解:∵和都是等腰直角三角形,
∴,
∴,,
∴,
∴(),
∴;
(2)解:由(1)得,
∴,,
∴,
∴,
又∵,,
∴,
∴;
(3)解:连接,,如图所示:
∵,,
∴,
∴,
∵,
∴ ,
∴,
由(1)得,
由(2)得∠°,
∴在中,,
即.
一.选择题(共10小题,满分30分,每小题3分)
1.下列二次根式中是最简二次根式的是( )
A. B. C. D.
2.实数a,b在数轴上的位置如图所示,则化简的结果是( )
A. B. C. D.0
3.一元二次方程有一个正根和一个负根,则a的取值范围是( )
A. B. C. D.
4.已知是整数,则正整数n的最小值为( )
A.2 B.3 C.4 D.5
5.等腰三角形的三边长分别为,,1,且关于的一元二次方程的两个根是和,则的值为( )
A.1 B.1或2 C.2 D.1且2
6.对于一元二次方程,下列说法:
①若,则;
②若方程有两个不相等的实根,则方程必有两个不相等的实根;
③若c是方程的一个根,则一定有成立;
②若是一元二次方程的根,则其中正确的( )
A.只有①②④ B.只有①②③ C.①②③④ D.只有①②
7.如图,在等腰直角中,,是的高线,E是边上一点,分别作于点F,于点G,几何原本中曾用该图证明了,若与的面积和为7.5,,则的长为( )
A. B. C. D.
8.设为正整数,,,,,…,….,已知,则( ).
A.1806 B.2005 C.3612 D.4011
9.如图,在平面直角坐标系中,将绕点A顺时针旋转到的位置,点B、O分别落在点、处,点在x轴上,再将绕点顺时针旋转到的位置,点在x轴上,将绕点顺时针旋转到的位置,点在x轴上,依次进行下去……,若点,.则点的坐标是( )
A. B. C. D.
10.如图,在中,点D,E分别是边、上的两点,连接,,,已知,,则的最小值是( )
A. B.10 C.9.6 D.
二.填空题(共6小题,满分18分,每小题3分)
11.若,则________.
12.如图,将放在正方形网格图中(图中每个小正方形的边长均为),点,, 恰好在网格图中的格点上,那么中边上的高是____.
13.将化简的结果是___________________.
14.已知关于x的一元二次方程x2+(2k+1)x+k2﹣2=0的两根x1和x2,且x12﹣2x1+2x2=x1x2,则k的值是_____.
15.如下图,直线,且与的距离为2,与的距离为6.把一块含有角的直角三角板如图放置,顶点,,恰好分别落在三条直线上,则的周长应为________.
16.如图是一张长方形纸片,已知,,点E、F在上,,,现要剪下一张等腰三角形纸片(),使点P落在长方形的某一条边上,则等腰三角形的边长是______.
三.解答题(共7小题,满分52分)
17.(6分)计算:
(1); (2).
18.(6分)解下列方程:
(1)(用配方法) (2)(用公式法)
(3) (4)
19.如图,已知四边形中,平分,,与互补,求证:.
20.(8分)关于的一元二次方程.
(1)求证:无论取任何实数,此方程总有两个不相等的实数根
(2)设该方程两个同号的实数根为,,试问是否存在使成立,若存在,求出的值,若不存在,请说明理由.
21.(8分)年9月,新冠病毒再次席卷贵阳,戴口罩是阻断病毒传播的重要措施之一,某商家对一款成本价为每盒元医用口罩进行销售,如果按每盒元销售,每天可卖出盒,通过市场调查发现,每盒口罩售价每降低1元,则日销售量增加2盒.
(1)若每盒售价降低x元,则日销售量可表示为 盒,每盒口罩的利润为 元.
(2)若日利润保持不变,商家想尽快销售完该款口罩,每盒售价应定为多少元?
22.(8分)请阅读下列材料:
形如的式子的化简,我们只要找到两个正数a,b,使,即,那么便有.
例如:化简.
解:首先把化为,这里,
由于,即,
所以.
请根据材料解答下列问题:
(1)填空:__________.
(2)化简:(请写出计算过程).
23.(8分)如图1,直角三角形和直角三角形的直角顶点重合,点在斜边上,,,连接AE.
(1)求证:.
(2)若,求的长.
(3)如图2,点也在边上,且在点A,D之间,若,求证:.
答案
一.选择题
1.B
【分析】根据最简二次根式的定义,即可进行解答.
【详解】解:A、不是最简二次根式,故A不符合题意;
B、是最简二次根式,故B符合题意;
C、不是最简二次根式,故C不符合题意;
D、不是最简二次根式,故D不符合题意;
故选:B.
2.A
【分析】先根据数轴判断出a、b和a-b的符号,然后根据二次根式的性质化简求值即可.
【详解】解:由数轴可知:a<0,b>0,a-b<0
∴
=
=-a-b+a-b
=
故选A.
3.A
【分析】设一元二次方程的两个根为,根据题意,求解即可.
【详解】设一元二次方程的两个根为,
根据题意,
∴解得.
故选A.
4.A
【分析】根据是整数,,推出是完全平方数,设,得到,根据与同奇同偶,,,或,,得到,或,推出n的最小正整数值是2.
【详解】∵是整数,且,
∴是完全平方数,
设(m是正整数),
则,
∵与同奇同偶,
∴,或,
∴,或,
∴,
∴n的最小正整数值是2.
故选:A.
5.C
【分析】分1为底边长或腰长两种情况考虑:当1为底时,由及即可求出、的值,利用三角形的三边关系确定此种情况存在,再利用根与系数的关系找出即可;当1为腰时,则、中有一个为1,则另一个为3,由1、1、3不能围成三角形可排除此种情况.综上即可得出结论.
【详解】解:当1为底边长时,则,,
.
,2,2能围成三角形,
,
解得:;
当1为腰长时,、中有一个为1,则另一个为3,
,1,3不能围成三角形,
此种情况不存在.
故选:C.
6.A
【分析】根据一元二次方程的根、一元二次方程的根的判别式、等式的性质解决此题.
【详解】①当x=1时,a×12+b×1+c=a+b+c=0,那么一元二次方程ax2+bx+c=0(a≠0)有两个不相等的实数根或有两个相等的实数根,此时b2-4ac≥0成立,那么①一定正确.
②方程ax2+c=0有两个不相等的实根,则-4ac>0,那么b2-4ac>0,故方程ax2+bx+c=0(a≠0)必有两个不相等的实根,进而推断出②正确.
③由c是方程ax2+bx+c=0的一个根,得ac2+bc+c=0.当c≠0,则ac+b+1=0;当c=0,则ac+b+1不一定等于0,那么③不一定正确.
④(2ax0+b)2=4a2x02+b2+4abx0,由b2-4ac=4a2x02+b2+4abx0,得ax02+bx0+c=0.由x0是一元二次方程ax2+bx+c=0的根,则ax02+bx0+c=0成立,那么④正确.
综上:正确的有①②④,共3个.
故选:A.
7.B
【分析】由,得,从而有,即可得出答案.
【详解】由题意知:与都是等腰直三角形,
,
∵,
∴,
∵,
∴,
∵,
∴,
故选:B
8.A
【分析】利用多项式的乘法把各数开方进行计算,然后求出A1,A2,A3的值,从而找出规律并写出规律表达式,再把k=100代入进行计算即可求解.
【详解】∵(n+3)(n-1)+4=n2+2n-3+4=n2+2n+1=(n+1)2,
∴A1=
∵(n+5)A1+4=(n+5)(n+1)+4=n2+6n+5+4=n2+6n+9=(n+3)2,
∴A2=
∵(n+7)A2+4=(n+7)(n+3)+4=n2+10n+21+4=n2+10n+25=(n+5)2,
∴A3=
依此类推,Ak=n+(2k-1)
∴A100=n+(2×100-1)=2005
解得,n=1806.
故选A.
9.C
【分析】首先根据已知求出三角形三边长度,然后通过旋转发现,…,由图象可知点在x轴上,,根据这个规律可以求得的坐标.
【详解】解:由图象可知点在x轴上,
,
,
,
,
,
.
故选C.
10.A
【分析】过点A作,并使得,连接,构造,然后得到,进而得知,连接,即可得知的长度即为的最小值,也就是的最小值,最后利用勾股定理求得的值即可得到答案.
【详解】解:如图,过点A作,并使得,连接,则,
∴,
∵在中,,
∴,
∵,,
∴,
∴,
∴,
连接,即可得知的长度即为的最小值,也就是的最小值,
∵,,,
∴,
∵,
∴,
∴的最小值是,故A正确.
故选:A.
二.填空题
11.1
【分析】根据二次根式的性质,求得,,即可求解.
【详解】解:由二次根式的性质可得,,,
解得,
则,
∴,
故答案为:1.
12.
【分析】根据所给出的图形求出的长以及的度数,再根据三角形的面积公式列出方程进行计算即可.
【详解】解:根据图形可得:,,
∴,
∴是直角三角形,且,
设中的高是x,
则,
∴,
解得,
故答案为:.
13..
【分析】根据二次根式的性质化简即可.
【详解】∵a<0.∴a-3<0,∴==.
故答案为.
14.-2或
【分析】先由x12-2x1+2x2=x1x2,得出x1-2=0或x1-x2=0,再分两种情况进行讨论:①如果x1-2=0,将x=2代入x2+(2k+1)x+k2-2=0,得4+2(2k+1)+k2-2=0,解方程求出k=-2;②如果x1-x2=0,那么△=0,解方程即可求解.
【详解】∵x12-2x1+2x2=x1x2,
x12-2x1+2x2-x1x2=0,
x1(x1-2)-x2(x1-2)=0,
(x1-2)(x1-x2)=0,
∴x1-2=0或x1-x2=0.
①如果x1-2=0,那么x1=2,
将x=2代入x2+(2k+1)x+k2-2=0,
得4+2(2k+1)+k2-2=0,
整理,得k2+4k+4=0,
解得k=-2;
②如果x1-x2=0,
则△=(2k+1)2-4(k2-2)=0.
解得: ,
∴k的值为-2或.
故答案为:-2或.
15.
【分析】作⊥于,作于,得出,,再证明,得出,,根据勾股定理求出,,即可得出结果.
【详解】解:作⊥于,作于,如图,
则,,,
∴,
由题意可知,是等腰直角三角形,
∴,,
∴,
∴,
在和中,,
∴,
∴,
∴,
∴,
则,
∴的周长为:.
故答案为:.
16.或或
【分析】分三种情况当,是等腰三角形时,当,是等腰三角形时,当,是等腰三角形时,利用等腰三角形的性质与勾股定理求解即可.
【详解】解:∵,,,
∴,
如图所示,当,是等腰三角形时,则;
如图所示,当,是等腰三角形时,则;
在中,由勾股定理得,
在中,由勾股定理得;
如图所示,当,是等腰三角形时,过点作于H,则四边形是矩形,
∴,
∴,
在中,由勾股定理得
综上所述,长是或或,
故答案为:或或.
三.解答题
17.(1)解:原式
;
(2)解:原式
.
18.(1)解:,
移项得:,
配方得:,
即:,
开平方得:,
解得:,.
(2)解:,
,
∴,
解得:,.
(3)解:,
将一元二次方程化为一般形式为:,
分解因式得:,
∴或,
解得:,.
(4)解:,
将一元二次方程化为一般形式为:,
分解因式得:,
∴或,
解得:,.
19.证明:过C点分别作的垂线,垂足分别为E、F,
∵为的平分线,,
∴.
而与互补,与也互补,
∴.
在与中,,
∴.
∴.
∵为的平分线,,
∴,
∴,
∵,
∴,
∴.
20.(1)证明:,
无论取任何实数,此方程总有两个不相等的实数根.
(2)由根与系数的关系可得:,,
,
则有,
,
整理得:,
解得:或,
由方程有两个同号的实数根可得:,即m-2>0,
m>2,
不存在m使成立.
21.(1)解:由题意可得,
∵每盒口罩售价每降低1元,则日销售量增加2盒,
∴若每盒售价降低x元,则日销售量为,
利润为:(元)
故答案为:,;
(2)解:由题意可得,
,
解得:,,
∵商家想尽快销售完该款口罩,
∴,
即售价为:(元),
答:每盒售价应定为元.
22.(1)解:,
故答案为:;
(2)解:由可得,这里,
∵,即,
∴.
23.(1)解:∵和都是等腰直角三角形,
∴,
∴,,
∴,
∴(),
∴;
(2)解:由(1)得,
∴,,
∴,
∴,
又∵,,
∴,
∴;
(3)解:连接,,如图所示:
∵,,
∴,
∴,
∵,
∴ ,
∴,
由(1)得,
由(2)得∠°,
∴在中,,
即.
同课章节目录
