【北师大版九上同步练习】 6.2 反比例函数图像和性质(含答案)
文档属性
| 名称 | 【北师大版九上同步练习】 6.2 反比例函数图像和性质(含答案) |
|
|
| 格式 | doc | ||
| 文件大小 | 15.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 17:06:22 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【北师大版九上同步练习】
6.2反比例函数图像和性质
一、填空题
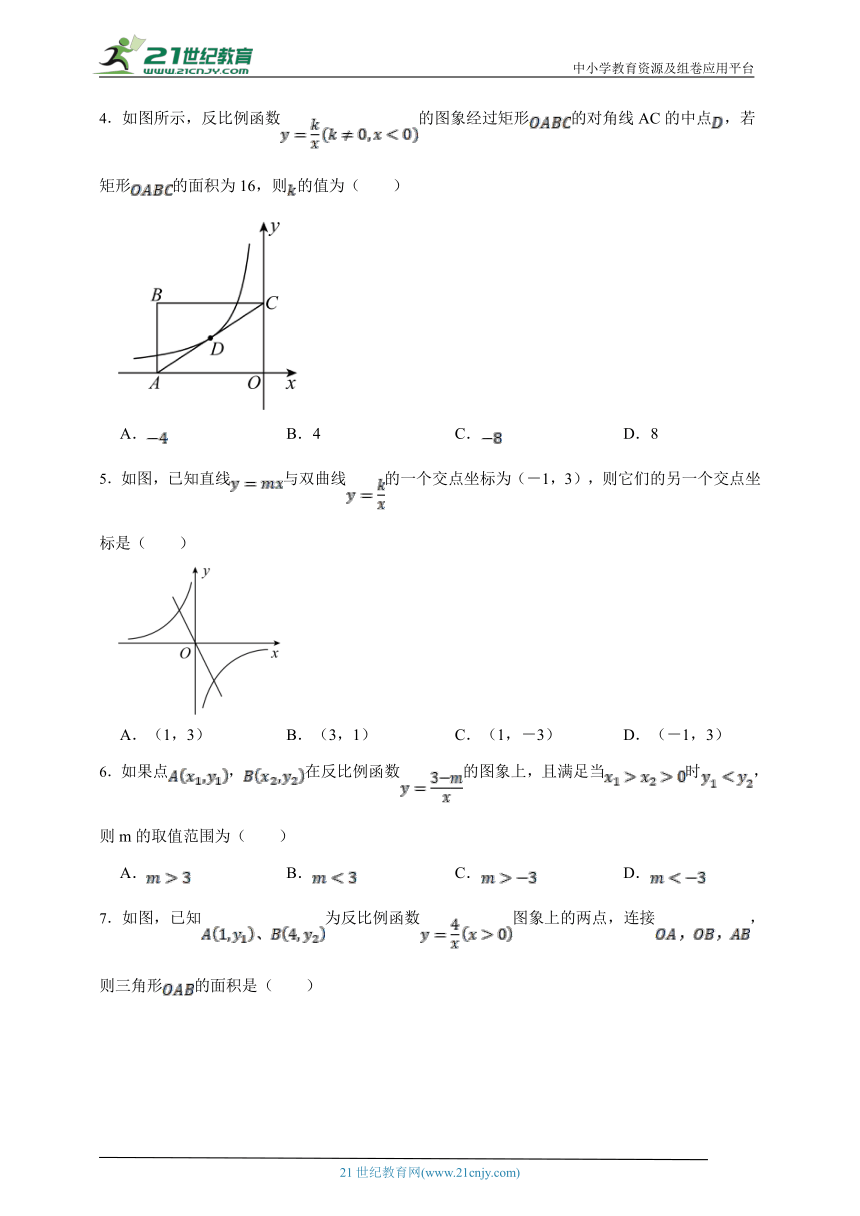
1. 如图,在平面直角坐标系中,点,,动点在线段上(不与端点重合),点绕点顺时针旋转得到点,若点在反比例函数的图象上,则的取值范围是 .
2.如图,顶点A落在轴上,斜边上的中线轴于点D、O为坐标原点,反比例函数经过直角顶点,若的面积为,则的值为 .
3.如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=(x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是 .
二、单选题
4.如图所示,反比例函数的图象经过矩形的对角线AC的中点,若矩形的面积为16,则的值为( )
A. B.4 C. D.8
5.如图,已知直线与双曲线的一个交点坐标为(-1,3),则它们的另一个交点坐标是( )
A.(1,3) B.(3,1) C.(1,-3) D.(-1,3)
6.如果点,在反比例函数的图象上,且满足当时,则m的取值范围为( )
A. B. C. D.
7.如图,已知为反比例函数图象上的两点,连接,则三角形的面积是( )
A.4 B. C. D.
8.已知在反比例函数(k为常数)图象上,,若,则的值是( )
A.0 B.负数 C.正数 D.非负数
三、解答题
9.已知在直角坐标系中一点 P(a,b),其中a,b可以取-2,-1.1,2中任意一个值(a≠b).求点P(a,b)恰好落在反比例函数y= 的图象上的概率.
10.如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x>0)的图象经过点C,交AB于点D.已知AB=8,BC=5.
(1)若OA=8,求k的值:
(2)连接OC,若BD=BC,求OC的长.
11.定义:在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足x,y,那么称点T是点A、B的“和美点”.
(1)已知A(﹣1,8),B(4,﹣2),C(2,4).请判断点C (填“是”或“不是”)A、B两点的“和美点”.
(2)平面直角坐标系中,有四个点A (8,﹣1),B(2,﹣4),C(﹣3,5),D(12,5),点P是点A、B的“和美点”,点Q是点C、D的“和美点”.求过P、Q两点的直线解析式.
(3)若反比例函数y图象上有两点A、B,点T是点A、B的“和美点”,试问点T的横、纵坐标的积是否为常数?若是常数,请求出这个常数;若不是常数,请说明理由.
四、计算题
12.在平面直角坐标系xOy中,一次函数 的图象与y轴交于点 ,与反比例函数 的图象交于点 .
(1)求反比例函数的表达式和一次函数表达式;
(2)若点C是y轴上一点,且 ,直接写出点C的坐标.
五、综合题
13.如图,反比例函数 的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
(1)图象的另一支在第 象限;在每个象限内, 随 的增大而 ,常数 的取值范围是 ;
(2)若此反比例函数的图象经过点 ,求 的值.
14.如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=2OB,反比例函数 在第一象限的图象经过正方形的顶点C.
(1)求点C的坐标;
(2)如图2,将正方形ABCD沿x轴向右平移得到正方形 A'B'CD',点 A'恰好落在反比例函数的图象上,求此时点 D'的坐标;
(3)在(2)的条件下,点P为y轴上一动点,平面内是否存在点Q,使以点O、A'、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.
15.阅读理解:
在平面直角坐标系中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P、Q为某矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为P、Q的“相关矩形”.如图①中的矩形为点P、Q的“相关矩形”
(1)已知点A的坐标为(0,1).
①若点B的坐标为(3,5),则点A、B的“相关矩形”的周长为 ▲ .
②若点C在直线y=5上.且点A、C的“相关矩形”为正方形,求直线AC的解析式.
(2)已知点M的坐标为(-2,4),点N的坐标为(-5,3),若使函数的图象与点M、N的“相关矩形”有两个公共点,直接写出k的取值范围.
六、实践探究题
16.【阅读理解】对于任意正实数a、b,∵ ≥0,∴a﹣ ≥0,∴a+b≥2 ,只有当a=b时,等号成立.
(1)【获得结论】在a+b≥2 (a、b均为正实数)中,若ab为定值p,则a+b≥2 ,只有当a=b时,a+b有最小值2 .
根据上述内容,回答下列问题:若m>0,只有当m= 时,m+ 有最小值 .
(2)【探索应用】如图,已知A(﹣3,0),B(0,﹣4),P为双曲线 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
17.阅读材料:
对于两个正数a、b,则 (当且仅当a=b时取等号).
当 为定值时, 有最小值;当 为定值时, 有最大值.
例如:已知 ,若 ,求 的最小值.
解:由 ≥ ,得 ≥ ,当且仅当 即 时, 有最小值,最小值为 .
根据上面的阅读材料回答下列问题:
(1)已知 ,若 ,则当 时, 有最小值,最小值为 ;
(2)已知 ,若 ,则 取何值时, 有最小值,最小值是多少?
(3)用长为 篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?
18.如图,点P是y轴正半轴上的一个动点,过点P作y轴的垂线,与反比例函数的图象交于点A.把直线l上方的反比例函数图象沿着直线l翻折,其它部分保持不变,所形成的新图象称为“的l镜像”.
(1)当时;
①点 “的l镜像”;(填“在”或“不在”)
②“的l镜像”与x轴交点坐标是 ;
(2)过y轴上的点作y轴垂线,与“的l镜像”交于点B、C,若,求的长.
答案解析部分
1.【答案】
【知识点】反比例函数的图象;反比例函数图象上点的坐标特征
2.【答案】10
【知识点】反比例函数系数k的几何意义;三角形的角平分线、中线和高
3.【答案】
【知识点】反比例函数系数k的几何意义;相似三角形的判定与性质;三角形的中位线定理
4.【答案】A
【知识点】反比例函数系数k的几何意义;矩形的性质
5.【答案】C
【知识点】反比例函数图象的对称性
6.【答案】B
【知识点】反比例函数的性质
7.【答案】D
【知识点】反比例函数系数k的几何意义
8.【答案】B
【知识点】反比例函数的图象;反比例函数的性质
9.【答案】解:将点P(a,b)代入反比例函数y= 中得,
b = ,
整理得:ab=2,
点P坐标乘积为2的情况如下表:
-2 -1 1 2
-2 2 -2 -4
-1 2 -1 -2
1 -2 -1 2
2 -4 -2 2
点P(a,b)恰好落在反比例函数y= 的图象上的概率为:.
【知识点】反比例函数的图象;列表法与树状图法;概率的简单应用
10.【答案】(1)解:作CE⊥AB,垂足为E,
∵AC=BC,AB=8,
∴AE=BE=4.
在Rt△BCE中,BC=5,BE=4,
∴CE===3,
∵OA=8,
∴C点的坐标为:(5,4),
∵反比例函数y=(x>0)的图象经过点C,
∴k=5×4=20,
(2)解:设A点的坐标为(m,0),
∵BD=BC=5,AB=8,
∴AD=3,
∴D,C两点的坐标分别为:(m,3),(m﹣3,4).
∵点C,D都在反比例函数y=(x>0)的图象上,
∴3m=4(m﹣3),
∴m=12,
∴C点的坐标为:(9,4),
∴OC==.
【知识点】等腰三角形的性质;勾股定理;反比例函数图象上点的坐标特征
11.【答案】(1)是
(2)解:∵点A (8,﹣1),B(2,﹣4),且点P是点A、B的“和美点”,
∴P(4,2).
∵点C(﹣3,5),D(12,5),且点Q是点C、D的“和美点”,
∴Q(6,5),
设直线PQ的解析式为y=kx+m,
∴,
∴,
∴直线PQ的解析式为yx﹣4;
(3)解:点T的横、纵坐标的积是常数4,
理由:设点A(n,),B(h,).
∵点T是点A、B的“和美点”,
∴T(,),
∴点T的横、纵坐标的积是: 4
【知识点】待定系数法求一次函数解析式;反比例函数图象上点的坐标特征;定义新运算
12.【答案】(1)∵双曲线 过 ,将 代入 ,解得: .
∴所求反比例函数表达式为: .
∵点 ,点 在直线 上,∴ , ,∴ ,∴所求一次函数表达式为 .
(2)由 , 可得: ,∴ .
又∵ ,∴ 或 ,∴ , 或 , .
【知识点】一次函数的图象;一次函数图象与坐标轴交点问题;反比例函数图象上点的坐标特征;平面直角坐标系的构成
13.【答案】(1)四;增大;
(2)解:把 代入 得到: ,则
故m的值为
【知识点】反比例函数的性质;反比例函数图象上点的坐标特征
14.【答案】(1)解:作CH⊥x轴于H,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBH=90°,
∵∠ABO+∠OAB=90°,
∴∠OAB=∠CBH,
∴△AOB≌△BHC(AAS),
∴BH=OA=6,CH=OB=3,
∴C(9,3);
(2)解:由(1)同理可得,点D(6,9),
∵点A'恰好落在反比例函数的图象上,
∴当y=6时,x=,
∴m=,
∴D'(6+,9),即D'(,9)
(3)解:Q(,)或(,-)或(-,6)或(,)
【知识点】反比例函数的图象;菱形的性质;正方形的性质;关于坐标轴对称的点的坐标特征;三角形全等的判定-AAS
15.【答案】(1)解:①14; ②设点C(a,5),
又∵点A的坐标为(0,1),点A、C的“相关矩形”为正方形,
∴|a-0|=|5-1|,
∴a=±4,
∴点C(4,5)或(-4,5),
设直线AC的解析式为y=kx+b,
若过点A,点C(4,5),
∴,
解得:,
∴直线AC的解析式为y=x+1,
若过点A,点C(-4,5),
∴,
解得:,
∴直线AC的解析式为y=-x+1,
综上所述:直线AC的解析式为y=-x+1或y=x+1;
(2)解:如图,
当y=的图象过点(-2,3)时,函数的图象与点M、N的“相关矩形”有1个公共点,
∴k=-2×3=6时,
当y=的图象过点(-5,4)时,函数的图象与点M、N的“相关矩形”有1个公共点,
∴k=-5×4=-20,
∴当-20<k<-6时,函数的图象与点M、N的“相关矩形”有两个公共点.
【知识点】待定系数法求一次函数解析式;矩形的性质;正方形的性质;反比例函数图象上点的坐标特征;定义新运算
16.【答案】(1)1;2
(2)解:设P(x, ),则C(x,0),D(0, ),
∴CA=x+3,BD= +4,
∴S四边形ABCD= CA×BD= (x+3)( +4),
化简得:S=2(x+ )+12,
∵x>0, >0,
∴x+ ≥2 =6,
只有当x= ,即x=3时,等号成立,
∴S≥2×6+12=24.
∴S四边形ABCD有最小值24,
此时,P(3,4),C(3,0),D(0,4),
AB=BC=CD=DA=5,
∴四边形ABCD是菱形
【知识点】菱形的判定;反比例函数图象上点的坐标特征
17.【答案】(1);12
(2)解:
由 得
当且仅当 ,即 时, 有最小值,最小值为9
答: 时, 有最小值,最小值是9
(3)解:设这个长方形花园的长为 ,则宽为
则所围的长方形花园面积为
由题意得: ,即
由 得 ,即
当且仅当 ,即 时, 取得最大值,最大值为
则当 , 时, 有最大值,最大值为625
答:当长方形花园的长、宽均为 时,所围的长方形花园面积最大,最大面积是
【知识点】反比例函数的性质;不等式的性质
18.【答案】(1)在;
(2)解:如图,①过轴上的点作轴垂线,与“的镜像”交于点、.
点,纵坐标为.
点在反比例函数图象上.
点坐标.
.
.
.
点坐标为.
当时,反比例函数的值.
点与点关于直线对称.
由“的镜像”定义得:.
的长为.
②当点,位置交换时,同理得的长为 .
的长为或.
【知识点】反比例函数图象上点的坐标特征
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版九上同步练习】
6.2反比例函数图像和性质
一、填空题
1. 如图,在平面直角坐标系中,点,,动点在线段上(不与端点重合),点绕点顺时针旋转得到点,若点在反比例函数的图象上,则的取值范围是 .
2.如图,顶点A落在轴上,斜边上的中线轴于点D、O为坐标原点,反比例函数经过直角顶点,若的面积为,则的值为 .
3.如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=(x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是 .
二、单选题
4.如图所示,反比例函数的图象经过矩形的对角线AC的中点,若矩形的面积为16,则的值为( )
A. B.4 C. D.8
5.如图,已知直线与双曲线的一个交点坐标为(-1,3),则它们的另一个交点坐标是( )
A.(1,3) B.(3,1) C.(1,-3) D.(-1,3)
6.如果点,在反比例函数的图象上,且满足当时,则m的取值范围为( )
A. B. C. D.
7.如图,已知为反比例函数图象上的两点,连接,则三角形的面积是( )
A.4 B. C. D.
8.已知在反比例函数(k为常数)图象上,,若,则的值是( )
A.0 B.负数 C.正数 D.非负数
三、解答题
9.已知在直角坐标系中一点 P(a,b),其中a,b可以取-2,-1.1,2中任意一个值(a≠b).求点P(a,b)恰好落在反比例函数y= 的图象上的概率.
10.如图,在△ABC中,AC=BC,AB⊥x轴,垂足为A.反比例函数y=(x>0)的图象经过点C,交AB于点D.已知AB=8,BC=5.
(1)若OA=8,求k的值:
(2)连接OC,若BD=BC,求OC的长.
11.定义:在平面直角坐标系中,对于任意两点A(a,b),B(c,d),若点T(x,y)满足x,y,那么称点T是点A、B的“和美点”.
(1)已知A(﹣1,8),B(4,﹣2),C(2,4).请判断点C (填“是”或“不是”)A、B两点的“和美点”.
(2)平面直角坐标系中,有四个点A (8,﹣1),B(2,﹣4),C(﹣3,5),D(12,5),点P是点A、B的“和美点”,点Q是点C、D的“和美点”.求过P、Q两点的直线解析式.
(3)若反比例函数y图象上有两点A、B,点T是点A、B的“和美点”,试问点T的横、纵坐标的积是否为常数?若是常数,请求出这个常数;若不是常数,请说明理由.
四、计算题
12.在平面直角坐标系xOy中,一次函数 的图象与y轴交于点 ,与反比例函数 的图象交于点 .
(1)求反比例函数的表达式和一次函数表达式;
(2)若点C是y轴上一点,且 ,直接写出点C的坐标.
五、综合题
13.如图,反比例函数 的图象的一支在平面直角坐标系中的位置如图所示,根据图象回答下列问题:
(1)图象的另一支在第 象限;在每个象限内, 随 的增大而 ,常数 的取值范围是 ;
(2)若此反比例函数的图象经过点 ,求 的值.
14.如图1,四边形ABCD为正方形,点A在y轴上,点B在x轴上,且OA=2OB,反比例函数 在第一象限的图象经过正方形的顶点C.
(1)求点C的坐标;
(2)如图2,将正方形ABCD沿x轴向右平移得到正方形 A'B'CD',点 A'恰好落在反比例函数的图象上,求此时点 D'的坐标;
(3)在(2)的条件下,点P为y轴上一动点,平面内是否存在点Q,使以点O、A'、P、Q为顶点的四边形为菱形,若存在,请直接写出点Q的坐标,若不存在,请说明理由.
15.阅读理解:
在平面直角坐标系中,点P的坐标为(x1,y1),点Q的坐标为(x2,y2),且x1≠x2,y1≠y2,若P、Q为某矩形的两个顶点,且该矩形的边均与某条坐标轴垂直,则称该矩形为P、Q的“相关矩形”.如图①中的矩形为点P、Q的“相关矩形”
(1)已知点A的坐标为(0,1).
①若点B的坐标为(3,5),则点A、B的“相关矩形”的周长为 ▲ .
②若点C在直线y=5上.且点A、C的“相关矩形”为正方形,求直线AC的解析式.
(2)已知点M的坐标为(-2,4),点N的坐标为(-5,3),若使函数的图象与点M、N的“相关矩形”有两个公共点,直接写出k的取值范围.
六、实践探究题
16.【阅读理解】对于任意正实数a、b,∵ ≥0,∴a﹣ ≥0,∴a+b≥2 ,只有当a=b时,等号成立.
(1)【获得结论】在a+b≥2 (a、b均为正实数)中,若ab为定值p,则a+b≥2 ,只有当a=b时,a+b有最小值2 .
根据上述内容,回答下列问题:若m>0,只有当m= 时,m+ 有最小值 .
(2)【探索应用】如图,已知A(﹣3,0),B(0,﹣4),P为双曲线 上的任意一点,过点P作PC⊥x轴于点C,PD⊥y轴于点D.求四边形ABCD面积的最小值,并说明此时四边形ABCD的形状.
17.阅读材料:
对于两个正数a、b,则 (当且仅当a=b时取等号).
当 为定值时, 有最小值;当 为定值时, 有最大值.
例如:已知 ,若 ,求 的最小值.
解:由 ≥ ,得 ≥ ,当且仅当 即 时, 有最小值,最小值为 .
根据上面的阅读材料回答下列问题:
(1)已知 ,若 ,则当 时, 有最小值,最小值为 ;
(2)已知 ,若 ,则 取何值时, 有最小值,最小值是多少?
(3)用长为 篱笆围一个长方形花园,问这个长方形花园的长、宽各为多少时,所围的长方形花园面积最大,最大面积是多少?
18.如图,点P是y轴正半轴上的一个动点,过点P作y轴的垂线,与反比例函数的图象交于点A.把直线l上方的反比例函数图象沿着直线l翻折,其它部分保持不变,所形成的新图象称为“的l镜像”.
(1)当时;
①点 “的l镜像”;(填“在”或“不在”)
②“的l镜像”与x轴交点坐标是 ;
(2)过y轴上的点作y轴垂线,与“的l镜像”交于点B、C,若,求的长.
答案解析部分
1.【答案】
【知识点】反比例函数的图象;反比例函数图象上点的坐标特征
2.【答案】10
【知识点】反比例函数系数k的几何意义;三角形的角平分线、中线和高
3.【答案】
【知识点】反比例函数系数k的几何意义;相似三角形的判定与性质;三角形的中位线定理
4.【答案】A
【知识点】反比例函数系数k的几何意义;矩形的性质
5.【答案】C
【知识点】反比例函数图象的对称性
6.【答案】B
【知识点】反比例函数的性质
7.【答案】D
【知识点】反比例函数系数k的几何意义
8.【答案】B
【知识点】反比例函数的图象;反比例函数的性质
9.【答案】解:将点P(a,b)代入反比例函数y= 中得,
b = ,
整理得:ab=2,
点P坐标乘积为2的情况如下表:
-2 -1 1 2
-2 2 -2 -4
-1 2 -1 -2
1 -2 -1 2
2 -4 -2 2
点P(a,b)恰好落在反比例函数y= 的图象上的概率为:.
【知识点】反比例函数的图象;列表法与树状图法;概率的简单应用
10.【答案】(1)解:作CE⊥AB,垂足为E,
∵AC=BC,AB=8,
∴AE=BE=4.
在Rt△BCE中,BC=5,BE=4,
∴CE===3,
∵OA=8,
∴C点的坐标为:(5,4),
∵反比例函数y=(x>0)的图象经过点C,
∴k=5×4=20,
(2)解:设A点的坐标为(m,0),
∵BD=BC=5,AB=8,
∴AD=3,
∴D,C两点的坐标分别为:(m,3),(m﹣3,4).
∵点C,D都在反比例函数y=(x>0)的图象上,
∴3m=4(m﹣3),
∴m=12,
∴C点的坐标为:(9,4),
∴OC==.
【知识点】等腰三角形的性质;勾股定理;反比例函数图象上点的坐标特征
11.【答案】(1)是
(2)解:∵点A (8,﹣1),B(2,﹣4),且点P是点A、B的“和美点”,
∴P(4,2).
∵点C(﹣3,5),D(12,5),且点Q是点C、D的“和美点”,
∴Q(6,5),
设直线PQ的解析式为y=kx+m,
∴,
∴,
∴直线PQ的解析式为yx﹣4;
(3)解:点T的横、纵坐标的积是常数4,
理由:设点A(n,),B(h,).
∵点T是点A、B的“和美点”,
∴T(,),
∴点T的横、纵坐标的积是: 4
【知识点】待定系数法求一次函数解析式;反比例函数图象上点的坐标特征;定义新运算
12.【答案】(1)∵双曲线 过 ,将 代入 ,解得: .
∴所求反比例函数表达式为: .
∵点 ,点 在直线 上,∴ , ,∴ ,∴所求一次函数表达式为 .
(2)由 , 可得: ,∴ .
又∵ ,∴ 或 ,∴ , 或 , .
【知识点】一次函数的图象;一次函数图象与坐标轴交点问题;反比例函数图象上点的坐标特征;平面直角坐标系的构成
13.【答案】(1)四;增大;
(2)解:把 代入 得到: ,则
故m的值为
【知识点】反比例函数的性质;反比例函数图象上点的坐标特征
14.【答案】(1)解:作CH⊥x轴于H,
∵四边形ABCD是正方形,
∴AB=BC,∠ABC=90°,
∴∠ABO+∠CBH=90°,
∵∠ABO+∠OAB=90°,
∴∠OAB=∠CBH,
∴△AOB≌△BHC(AAS),
∴BH=OA=6,CH=OB=3,
∴C(9,3);
(2)解:由(1)同理可得,点D(6,9),
∵点A'恰好落在反比例函数的图象上,
∴当y=6时,x=,
∴m=,
∴D'(6+,9),即D'(,9)
(3)解:Q(,)或(,-)或(-,6)或(,)
【知识点】反比例函数的图象;菱形的性质;正方形的性质;关于坐标轴对称的点的坐标特征;三角形全等的判定-AAS
15.【答案】(1)解:①14; ②设点C(a,5),
又∵点A的坐标为(0,1),点A、C的“相关矩形”为正方形,
∴|a-0|=|5-1|,
∴a=±4,
∴点C(4,5)或(-4,5),
设直线AC的解析式为y=kx+b,
若过点A,点C(4,5),
∴,
解得:,
∴直线AC的解析式为y=x+1,
若过点A,点C(-4,5),
∴,
解得:,
∴直线AC的解析式为y=-x+1,
综上所述:直线AC的解析式为y=-x+1或y=x+1;
(2)解:如图,
当y=的图象过点(-2,3)时,函数的图象与点M、N的“相关矩形”有1个公共点,
∴k=-2×3=6时,
当y=的图象过点(-5,4)时,函数的图象与点M、N的“相关矩形”有1个公共点,
∴k=-5×4=-20,
∴当-20<k<-6时,函数的图象与点M、N的“相关矩形”有两个公共点.
【知识点】待定系数法求一次函数解析式;矩形的性质;正方形的性质;反比例函数图象上点的坐标特征;定义新运算
16.【答案】(1)1;2
(2)解:设P(x, ),则C(x,0),D(0, ),
∴CA=x+3,BD= +4,
∴S四边形ABCD= CA×BD= (x+3)( +4),
化简得:S=2(x+ )+12,
∵x>0, >0,
∴x+ ≥2 =6,
只有当x= ,即x=3时,等号成立,
∴S≥2×6+12=24.
∴S四边形ABCD有最小值24,
此时,P(3,4),C(3,0),D(0,4),
AB=BC=CD=DA=5,
∴四边形ABCD是菱形
【知识点】菱形的判定;反比例函数图象上点的坐标特征
17.【答案】(1);12
(2)解:
由 得
当且仅当 ,即 时, 有最小值,最小值为9
答: 时, 有最小值,最小值是9
(3)解:设这个长方形花园的长为 ,则宽为
则所围的长方形花园面积为
由题意得: ,即
由 得 ,即
当且仅当 ,即 时, 取得最大值,最大值为
则当 , 时, 有最大值,最大值为625
答:当长方形花园的长、宽均为 时,所围的长方形花园面积最大,最大面积是
【知识点】反比例函数的性质;不等式的性质
18.【答案】(1)在;
(2)解:如图,①过轴上的点作轴垂线,与“的镜像”交于点、.
点,纵坐标为.
点在反比例函数图象上.
点坐标.
.
.
.
点坐标为.
当时,反比例函数的值.
点与点关于直线对称.
由“的镜像”定义得:.
的长为.
②当点,位置交换时,同理得的长为 .
的长为或.
【知识点】反比例函数图象上点的坐标特征
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
