【北师大版九上同步练习】 第六章 反比例函数(能力提升)检测题(含答案)
文档属性
| 名称 | 【北师大版九上同步练习】 第六章 反比例函数(能力提升)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 18.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 17:14:14 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【北师大版九上同步练习】
第六章反比例函数(能力提升)检测题
一、填空题
1.图1是由两个全等直角三角形和两个长方形组成的□ABCD,将其剪拼成不重叠,无缝隙的大正方形(如图2).记①,②,③,④的面积分别为S1,S2,S3,S4,已知S3=4S2.
(1) = ;
(2)若□ABCD的周长比长方形③的周长大18,则BC为 .
2.如图,点是反比倒函数上一动点,点的坐标为,过点作轴,垂足为点,以BA、BC为边作矩形ABCD,将矩形ABCD绕点顺时旋转得到矩形FECG,在点运动的过程中,点的对应点坐标为,则与满足的关系式为 .
3.如图,反比例函数的图象经过点,,.过点作轴于点,连结,并延长交于点.若是的中点,则的值为 (结果用含的代数式表示).
二、单选题
4.如图,在直角坐标系中,一次函数与反比例函数的图象交于A,B两点,下列结论正确的是( )
A.当时, B.当时,
C.当时, D.当时,
5.反比例函数与直线相交于点A,A点的横坐标为-1,则此反比例函数的解析式为( )
A. B. C. D.
6.已知近视眼镜的度数y(度)与镜片焦距x(米)之间成反比例函数关系,如图所示,则眼镜度数y与镜片焦距x之间的函数关系式是( )
A. B. C. D.
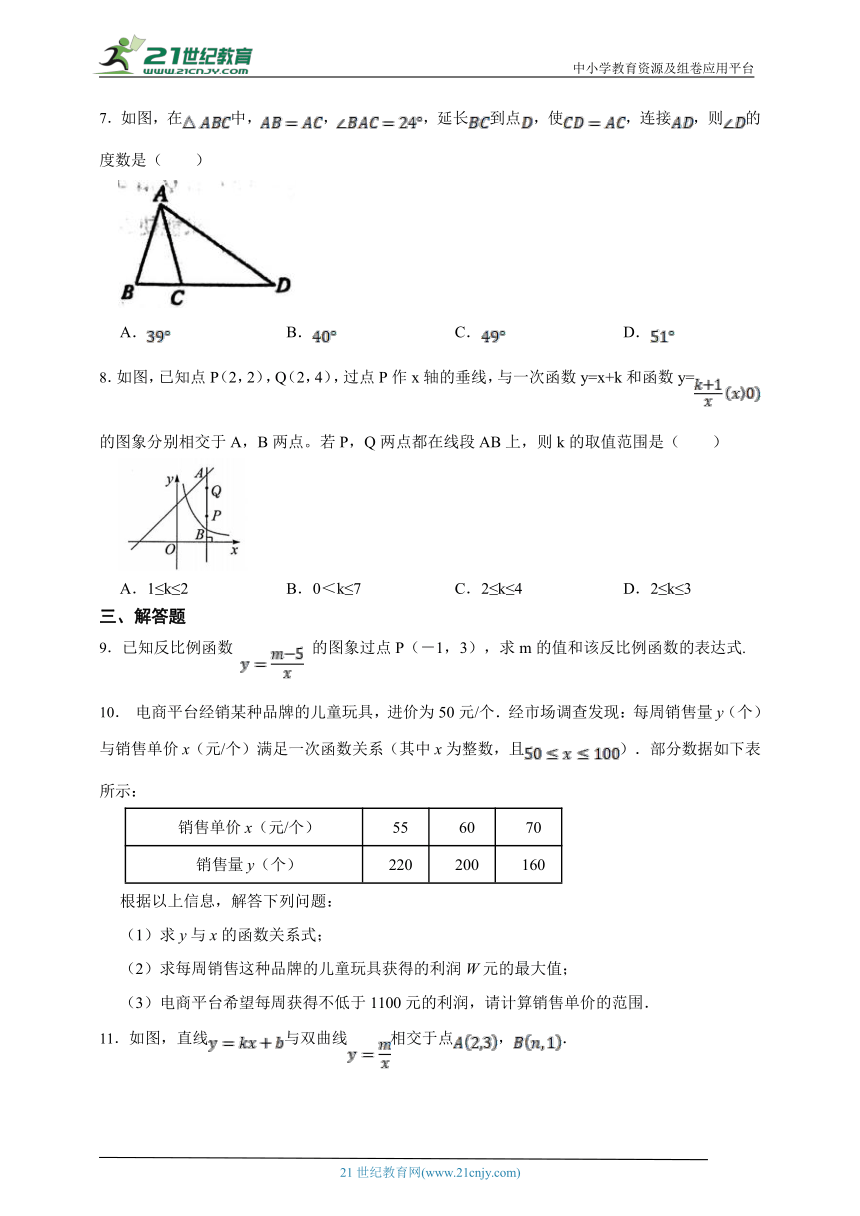
7.如图,在中,,,延长到点,使,连接,则的度数是( )
A. B. C. D.
8.如图,已知点P(2,2),Q(2,4),过点P作x轴的垂线,与一次函数y=x+k和函数y=的图象分别相交于A,B两点。若P,Q两点都在线段AB上,则k的取值范围是( )
A.1≤k≤2 B.0<k≤7 C.2≤k≤4 D.2≤k≤3
三、解答题
9.已知反比例函数 的图象过点P(-1,3),求m的值和该反比例函数的表达式.
10. 电商平台经销某种品牌的儿童玩具,进价为50元/个.经市场调查发现:每周销售量y(个)与销售单价x(元/个)满足一次函数关系(其中x为整数,且).部分数据如下表所示:
销售单价x(元/个) 55 60 70
销售量y(个) 220 200 160
根据以上信息,解答下列问题:
(1)求y与x的函数关系式;
(2)求每周销售这种品牌的儿童玩具获得的利润W元的最大值;
(3)电商平台希望每周获得不低于1100元的利润,请计算销售单价的范围.
11.如图,直线与双曲线相交于点,.
(1)求双曲线及直线对应的函数表达式;
(2)将直线向下平移至处,其中点,点在轴上.连接,,求的面积;
(3)请直接写出关于的不等式的解集.
四、计算题
12.
(1)计算: ;
(2)先化简,再求值: (x,y)是函数y=2x与 的图象的交点坐标.
五、综合题
13.如图,A、B两地相距120千米,甲、乙两人骑车同时分别从A、B两地相向而行匀速行驶,设他们各自距A地的距离S(千米)都是骑车时间t的一次函数,并回答下列问题:
(1)甲的速度为 千米/小时,乙的速度为 千米/小时;
(2)求运动过程中的函数解析式.
14.在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润
15.如图,在平面直角坐标系中,抛物线交轴于点A,交轴于点和点,连接、、,与轴交于点.
(1)求抛物线表达式;
(2)点,点在轴上,点在平面内,若,且四边形是平行四边形.
①求点的坐标;
②设射线与相交于点,交于点,将绕点旋转一周,旋转后的三角形记为,求的最小值.
六、实践探究题
16.背景:点A在反比例函数y=(k>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形.如图1,点A在第一象限内,当AC=4时,小李测得CD=3.
探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系.请帮助小李解决下列问题.
(1)求k的值.
(2)设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”.如图2,小李画出了x>0时“Z函数”的图象.
①求这个“Z函数”的表达式.
②补画x<0时“Z函数”的图象,并写出这个函数的性质(两条即可).
③过点(3,2)作一直线,与这个“Z函数”图象仅有一个交点,求该交点的横坐标.
17.⑴平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形 .
⑵有 角对应相等的两个三角形相似.
⑶课本第132页例1构造了相似三角形求河宽,你还有其他方法吗?(画出图形,简要说明).
18.
(1)【基本模型】如图1,矩形中,,,交于点E,则的值是 .
(2)【类比探究】如图2,中,,,,D为边上一点,连接,,交于点E,若,求的长.
(3)【拓展应用】如图3,在矩形中,,点F,G分别在上,以为折痕,将四边形翻折,使顶点A落在上的点E处,且,连接,设的面积为,的面积为,的面积为,若,请直接写出的值.
答案解析部分
1.【答案】(1)3:2
(2)
【知识点】平行四边形的性质;正方形的性质
2.【答案】
【知识点】反比例函数与一次函数的交点问题;矩形的性质;旋转的性质;反比例函数图象上点的坐标特征
3.【答案】
【知识点】反比例函数系数k的几何意义;相似三角形的判定与性质
4.【答案】B
【知识点】反比例函数与一次函数的交点问题
5.【答案】C
【知识点】反比例函数与一次函数的交点问题
6.【答案】C
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
7.【答案】A
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的性质
8.【答案】D
【知识点】反比例函数与一次函数的交点问题
9.【答案】解:把点P(-1,3)代入 ,得 .解得 .
把m=2代入 ,得 ,即 .
∴反比例函数的表达式为 .
【知识点】待定系数法求反比例函数解析式
10.【答案】(1)解:.
(2)解:,∵,
∴由二次函数的性质可知,时,W有最大值,
(元).
(3)解:当时,,
解这个方程得,,,因为,,
结合二次函数的图象分析,
电商平台希望每周获得不低于1100元利润,销售单价x的范围是:.
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
11.【答案】(1),
(2)
(3)或
【知识点】反比例函数与一次函数的交点问题
12.【答案】(1)解:原式=1+9 +(1- ×18)
=1+9 -1=9
(2)解:由已知可得:
,
解之可得: 或 ,
∵原式=
=
=y-x,
∴当 时,原式=2-1=1;
当 时,原式=-2-(-1)=-1;
∴原式的值为1或-1.
【知识点】实数的运算;反比例函数与一次函数的交点问题
13.【答案】(1)15;25
(2)设直线的解析式为
解得:
函数解析式为
【知识点】一次函数的实际应用
14.【答案】(1)解:y是x的一次函数,设y=kx+b,
∵图象过点(10,300),(12,240),
∴ ,解得 .∴y=-30x+600.
当x=14时,y=180;当x=16时,y=120,
∴点(14,180),(16,120)均在函数y=-30x+600图象上.
∴y与x之间的函数关系式为y=-30x+600.
(2)解:∵w=(x-6)(-30x+600)=-30x2+780x-3600,
∴w与x之间的函数关系式为w=-30x2+780x-3600.
(3)解:由题意得:6(-30x+600)≤900,解得x≥15.
w=-30x2+780x-3600图象对称轴为: .
∵a=-30<0,∴抛物线开口向下,当x≥15时,w随x增大而减小.
∴当x=15时,w最大=1350.
∴以15元/个的价格销售这批许愿瓶可获得最大利润1350元.
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
15.【答案】(1)
(2);
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式
16.【答案】(1)解:,,
,
四边形是正方形,
,
轴,轴,
,
点是反比例函数的图象上的点,
.
(2)①点是反比例函数的图象上的点,
,
,
,
②如图,
性质:1、函数图象与x轴有2个交点;2、当x<0时,z随x的增大而增大.
③ i)当直线轴时,直线与Z函数图象只有一个交点,且交点横坐标为3;
ii)当直线l不平行y轴时,设直线解析式为,
把点代入解析式得,
,
直线l与Z函数图象只有一个交点,
只有一个解,
化简得,
当时,该方程为一元二次方程,
,
解得,,
当时,原方程可化为,解得,
当时,原方程可化为,解得;
当时,该方程为一元一次方程,则,解得,
综上所述,该交点横坐标为2或3或4或6.
【知识点】反比例函数的性质;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;正方形的性质
17.【答案】解:⑴相似;
⑵两个
⑶①方法1(课本第132页例1的方法):通过构造相似三角形;
如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点 A,再在河的这一边选点 B 和 C,使 AB⊥BC,然后,再选点 E,使 EC ⊥ BC ,用视线确定 BC 和 AE 的交点 D. 此时测得BD,CD,EC的长,证明△ABD∽△ECD,利用相似求出AB的长即可.
证明过程:∵∠B=∠C=90°,∠ADB=∠CDE,
∴△ABD∽△ECD,
∴AB:CE=BD:CD,即可求出AB的长;
②方法2:通过构造全等三角形
如图,在河对岸选点A,在河这岸选点B,使AB垂直于河岸在河这岸选一点C(异于点B),用测角器测出∠BCA的度数,然后在BC的另一侧作出∠BCD=∠BCA,使点D、B、A在同一直线上,则线段BD的长就是AB的长.
证明过程:∵∠ABC=∠DBC=90°,BC=BC,∠BCA=∠BCD.
∴△BCA≌△BCD(ASA).
故BD=AB.
③方法3:通过构造全等三角形
如图,在河对岸选点A.,河这岸选点B,使AB垂直于河岸;在河这岸取点C和D,使DC= BC;在CD的垂线上取点E,使点E、 C、A在同一直线上,则DE的长就是AB的长.
证明过程:∵∠EDC=∠ABC=90°,DC=BC,∠DCE=∠BCA.
∴△EDC≌△ABC(ASA),
故DE=AB.
④方法4:通过构造等腰直角三角形
如图,在对面河岸选一定点A,利用测角器在河这岸选一点B,然后在河这岸选一点C,使得∠BCA=45°,则BC的长就是河的宽度AB.
证明过程:∵AB⊥BC,∠BCA=45°,
∴ABC为等腰直角三角形,
故BC=AB.
【知识点】相似三角形的判定;相似三角形的应用
18.【答案】(1)
(2)解:过点A,D作的垂线,垂足分别为,
,,,
,
,
,
,
,
,
,
,
,
∴,
∴,
设,则 ,
,
,
,
,
,
,
,
∴
(3)解:连接 ,
设 , 则 ,
,即 ,
解得 ,
,
,
,
,
,
,
,,,
,,,
,
,
,
设,
,,
,
,
,即,
(舍去),
,
过点作,垂足为Q,
由折叠的性质得到,
,
,
,
,
,
,
四边形是矩形,
,
.
【知识点】勾股定理;矩形的判定与性质;相似三角形的判定与性质;解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版九上同步练习】
第六章反比例函数(能力提升)检测题
一、填空题
1.图1是由两个全等直角三角形和两个长方形组成的□ABCD,将其剪拼成不重叠,无缝隙的大正方形(如图2).记①,②,③,④的面积分别为S1,S2,S3,S4,已知S3=4S2.
(1) = ;
(2)若□ABCD的周长比长方形③的周长大18,则BC为 .
2.如图,点是反比倒函数上一动点,点的坐标为,过点作轴,垂足为点,以BA、BC为边作矩形ABCD,将矩形ABCD绕点顺时旋转得到矩形FECG,在点运动的过程中,点的对应点坐标为,则与满足的关系式为 .
3.如图,反比例函数的图象经过点,,.过点作轴于点,连结,并延长交于点.若是的中点,则的值为 (结果用含的代数式表示).
二、单选题
4.如图,在直角坐标系中,一次函数与反比例函数的图象交于A,B两点,下列结论正确的是( )
A.当时, B.当时,
C.当时, D.当时,
5.反比例函数与直线相交于点A,A点的横坐标为-1,则此反比例函数的解析式为( )
A. B. C. D.
6.已知近视眼镜的度数y(度)与镜片焦距x(米)之间成反比例函数关系,如图所示,则眼镜度数y与镜片焦距x之间的函数关系式是( )
A. B. C. D.
7.如图,在中,,,延长到点,使,连接,则的度数是( )
A. B. C. D.
8.如图,已知点P(2,2),Q(2,4),过点P作x轴的垂线,与一次函数y=x+k和函数y=的图象分别相交于A,B两点。若P,Q两点都在线段AB上,则k的取值范围是( )
A.1≤k≤2 B.0<k≤7 C.2≤k≤4 D.2≤k≤3
三、解答题
9.已知反比例函数 的图象过点P(-1,3),求m的值和该反比例函数的表达式.
10. 电商平台经销某种品牌的儿童玩具,进价为50元/个.经市场调查发现:每周销售量y(个)与销售单价x(元/个)满足一次函数关系(其中x为整数,且).部分数据如下表所示:
销售单价x(元/个) 55 60 70
销售量y(个) 220 200 160
根据以上信息,解答下列问题:
(1)求y与x的函数关系式;
(2)求每周销售这种品牌的儿童玩具获得的利润W元的最大值;
(3)电商平台希望每周获得不低于1100元的利润,请计算销售单价的范围.
11.如图,直线与双曲线相交于点,.
(1)求双曲线及直线对应的函数表达式;
(2)将直线向下平移至处,其中点,点在轴上.连接,,求的面积;
(3)请直接写出关于的不等式的解集.
四、计算题
12.
(1)计算: ;
(2)先化简,再求值: (x,y)是函数y=2x与 的图象的交点坐标.
五、综合题
13.如图,A、B两地相距120千米,甲、乙两人骑车同时分别从A、B两地相向而行匀速行驶,设他们各自距A地的距离S(千米)都是骑车时间t的一次函数,并回答下列问题:
(1)甲的速度为 千米/小时,乙的速度为 千米/小时;
(2)求运动过程中的函数解析式.
14.在“母亲节”期间,某校部分团员参加社会公益活动,准备购进一批许愿瓶进行
销售,并将所得利润捐给慈善机构.根据市场调查,这种许愿瓶一段时间内的销售量y(个)于销售单价x(元/个)之间的对应关系如图所示.
(1)试判断y与x之间的函数关系,并求出函数关系式;
(2)若许愿瓶的进价为6元/个,按照上述市场调查销售规律,求利润w(元)与销售单价x(元/个)之间的
函数关系式;
(3)若许愿瓶的进货成本不超过900元,要想获得最大利润,试求此时这种许愿瓶的销售单价,并求出
最大利润
15.如图,在平面直角坐标系中,抛物线交轴于点A,交轴于点和点,连接、、,与轴交于点.
(1)求抛物线表达式;
(2)点,点在轴上,点在平面内,若,且四边形是平行四边形.
①求点的坐标;
②设射线与相交于点,交于点,将绕点旋转一周,旋转后的三角形记为,求的最小值.
六、实践探究题
16.背景:点A在反比例函数y=(k>0)的图象上,AB⊥x轴于点B,AC⊥y轴于点C,分别在射线AC,BO上取点D,E,使得四边形ABED为正方形.如图1,点A在第一象限内,当AC=4时,小李测得CD=3.
探究:通过改变点A的位置,小李发现点D,A的横坐标之间存在函数关系.请帮助小李解决下列问题.
(1)求k的值.
(2)设点A,D的横坐标分别为x,z,将z关于x的函数称为“Z函数”.如图2,小李画出了x>0时“Z函数”的图象.
①求这个“Z函数”的表达式.
②补画x<0时“Z函数”的图象,并写出这个函数的性质(两条即可).
③过点(3,2)作一直线,与这个“Z函数”图象仅有一个交点,求该交点的横坐标.
17.⑴平行于三角形一边的直线和其他两边相交,所构成的三角形与原三角形 .
⑵有 角对应相等的两个三角形相似.
⑶课本第132页例1构造了相似三角形求河宽,你还有其他方法吗?(画出图形,简要说明).
18.
(1)【基本模型】如图1,矩形中,,,交于点E,则的值是 .
(2)【类比探究】如图2,中,,,,D为边上一点,连接,,交于点E,若,求的长.
(3)【拓展应用】如图3,在矩形中,,点F,G分别在上,以为折痕,将四边形翻折,使顶点A落在上的点E处,且,连接,设的面积为,的面积为,的面积为,若,请直接写出的值.
答案解析部分
1.【答案】(1)3:2
(2)
【知识点】平行四边形的性质;正方形的性质
2.【答案】
【知识点】反比例函数与一次函数的交点问题;矩形的性质;旋转的性质;反比例函数图象上点的坐标特征
3.【答案】
【知识点】反比例函数系数k的几何意义;相似三角形的判定与性质
4.【答案】B
【知识点】反比例函数与一次函数的交点问题
5.【答案】C
【知识点】反比例函数与一次函数的交点问题
6.【答案】C
【知识点】待定系数法求反比例函数解析式;反比例函数的实际应用
7.【答案】A
【知识点】三角形内角和定理;三角形的外角性质;等腰三角形的性质
8.【答案】D
【知识点】反比例函数与一次函数的交点问题
9.【答案】解:把点P(-1,3)代入 ,得 .解得 .
把m=2代入 ,得 ,即 .
∴反比例函数的表达式为 .
【知识点】待定系数法求反比例函数解析式
10.【答案】(1)解:.
(2)解:,∵,
∴由二次函数的性质可知,时,W有最大值,
(元).
(3)解:当时,,
解这个方程得,,,因为,,
结合二次函数的图象分析,
电商平台希望每周获得不低于1100元利润,销售单价x的范围是:.
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
11.【答案】(1),
(2)
(3)或
【知识点】反比例函数与一次函数的交点问题
12.【答案】(1)解:原式=1+9 +(1- ×18)
=1+9 -1=9
(2)解:由已知可得:
,
解之可得: 或 ,
∵原式=
=
=y-x,
∴当 时,原式=2-1=1;
当 时,原式=-2-(-1)=-1;
∴原式的值为1或-1.
【知识点】实数的运算;反比例函数与一次函数的交点问题
13.【答案】(1)15;25
(2)设直线的解析式为
解得:
函数解析式为
【知识点】一次函数的实际应用
14.【答案】(1)解:y是x的一次函数,设y=kx+b,
∵图象过点(10,300),(12,240),
∴ ,解得 .∴y=-30x+600.
当x=14时,y=180;当x=16时,y=120,
∴点(14,180),(16,120)均在函数y=-30x+600图象上.
∴y与x之间的函数关系式为y=-30x+600.
(2)解:∵w=(x-6)(-30x+600)=-30x2+780x-3600,
∴w与x之间的函数关系式为w=-30x2+780x-3600.
(3)解:由题意得:6(-30x+600)≤900,解得x≥15.
w=-30x2+780x-3600图象对称轴为: .
∵a=-30<0,∴抛物线开口向下,当x≥15时,w随x增大而减小.
∴当x=15时,w最大=1350.
∴以15元/个的价格销售这批许愿瓶可获得最大利润1350元.
【知识点】待定系数法求一次函数解析式;二次函数的实际应用-销售问题
15.【答案】(1)
(2);
【知识点】待定系数法求一次函数解析式;待定系数法求二次函数解析式
16.【答案】(1)解:,,
,
四边形是正方形,
,
轴,轴,
,
点是反比例函数的图象上的点,
.
(2)①点是反比例函数的图象上的点,
,
,
,
②如图,
性质:1、函数图象与x轴有2个交点;2、当x<0时,z随x的增大而增大.
③ i)当直线轴时,直线与Z函数图象只有一个交点,且交点横坐标为3;
ii)当直线l不平行y轴时,设直线解析式为,
把点代入解析式得,
,
直线l与Z函数图象只有一个交点,
只有一个解,
化简得,
当时,该方程为一元二次方程,
,
解得,,
当时,原方程可化为,解得,
当时,原方程可化为,解得;
当时,该方程为一元一次方程,则,解得,
综上所述,该交点横坐标为2或3或4或6.
【知识点】反比例函数的性质;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题;正方形的性质
17.【答案】解:⑴相似;
⑵两个
⑶①方法1(课本第132页例1的方法):通过构造相似三角形;
如图,为了估算河的宽度,我们可以在河对岸选定一个目标作为点 A,再在河的这一边选点 B 和 C,使 AB⊥BC,然后,再选点 E,使 EC ⊥ BC ,用视线确定 BC 和 AE 的交点 D. 此时测得BD,CD,EC的长,证明△ABD∽△ECD,利用相似求出AB的长即可.
证明过程:∵∠B=∠C=90°,∠ADB=∠CDE,
∴△ABD∽△ECD,
∴AB:CE=BD:CD,即可求出AB的长;
②方法2:通过构造全等三角形
如图,在河对岸选点A,在河这岸选点B,使AB垂直于河岸在河这岸选一点C(异于点B),用测角器测出∠BCA的度数,然后在BC的另一侧作出∠BCD=∠BCA,使点D、B、A在同一直线上,则线段BD的长就是AB的长.
证明过程:∵∠ABC=∠DBC=90°,BC=BC,∠BCA=∠BCD.
∴△BCA≌△BCD(ASA).
故BD=AB.
③方法3:通过构造全等三角形
如图,在河对岸选点A.,河这岸选点B,使AB垂直于河岸;在河这岸取点C和D,使DC= BC;在CD的垂线上取点E,使点E、 C、A在同一直线上,则DE的长就是AB的长.
证明过程:∵∠EDC=∠ABC=90°,DC=BC,∠DCE=∠BCA.
∴△EDC≌△ABC(ASA),
故DE=AB.
④方法4:通过构造等腰直角三角形
如图,在对面河岸选一定点A,利用测角器在河这岸选一点B,然后在河这岸选一点C,使得∠BCA=45°,则BC的长就是河的宽度AB.
证明过程:∵AB⊥BC,∠BCA=45°,
∴ABC为等腰直角三角形,
故BC=AB.
【知识点】相似三角形的判定;相似三角形的应用
18.【答案】(1)
(2)解:过点A,D作的垂线,垂足分别为,
,,,
,
,
,
,
,
,
,
,
,
∴,
∴,
设,则 ,
,
,
,
,
,
,
,
∴
(3)解:连接 ,
设 , 则 ,
,即 ,
解得 ,
,
,
,
,
,
,
,,,
,,,
,
,
,
设,
,,
,
,
,即,
(舍去),
,
过点作,垂足为Q,
由折叠的性质得到,
,
,
,
,
,
,
四边形是矩形,
,
.
【知识点】勾股定理;矩形的判定与性质;相似三角形的判定与性质;解直角三角形
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
