【北师大版九上同步练习】 第六章 反比例函数(培优)检测题(含答案)
文档属性
| 名称 | 【北师大版九上同步练习】 第六章 反比例函数(培优)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 15.8MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 17:15:16 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
【北师大版九上同步练习】
第六章反比例函数(培优)检测题
一、填空题
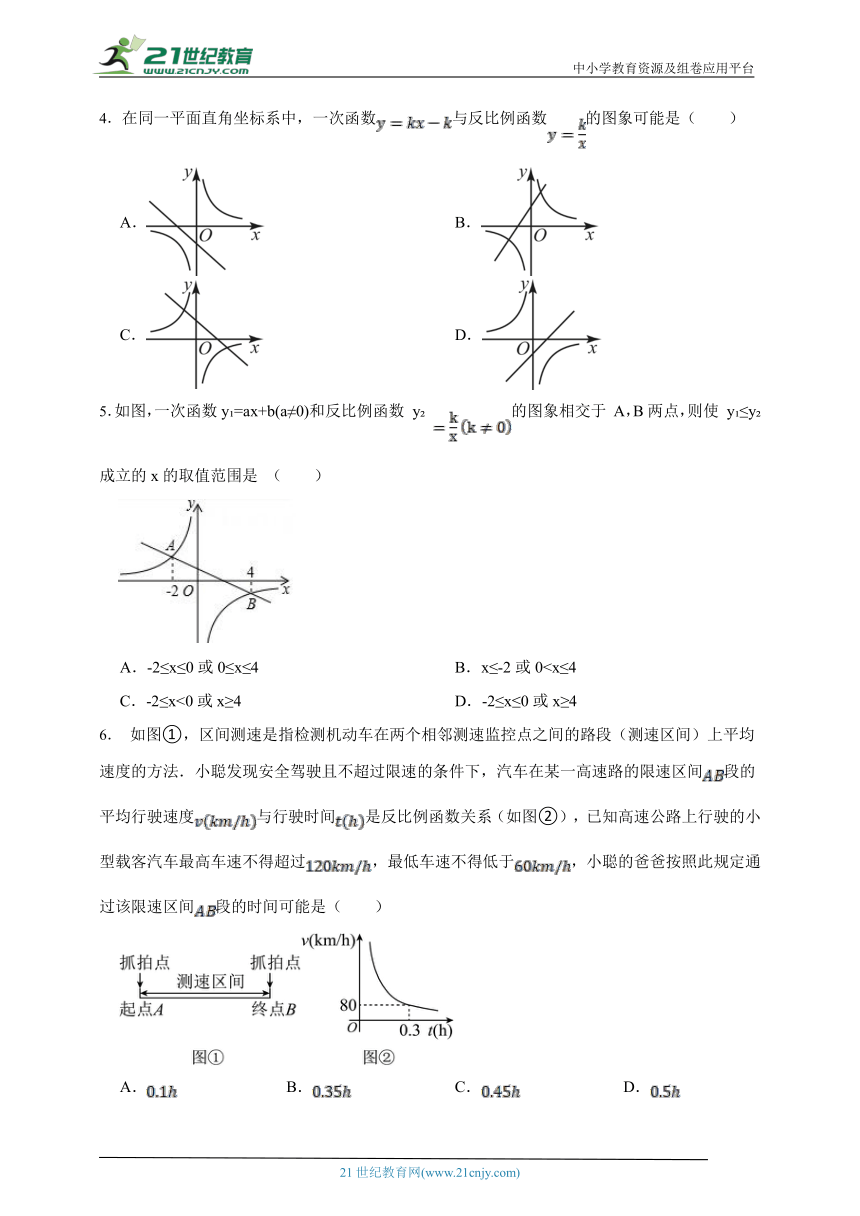
1.如图,正方形边长为6,点为边的中点,连接,将沿翻折得到,延长交于点,则长为 .
2.将一张长方形纸片ABCD(长方形的四个内角都是直角)按如图所示操作
①将DA沿DP向内折叠,使点A落在点A1处;
②将DP沿DA1向内继续折叠,使点P落在点P1处,折痕与边AB交于点M.若P1MAB,则∠DP1M的度数等于 .
3.如图,在边长为6的正方形内部存在一动点,且满足,连接,则的最大值是 .
二、单选题
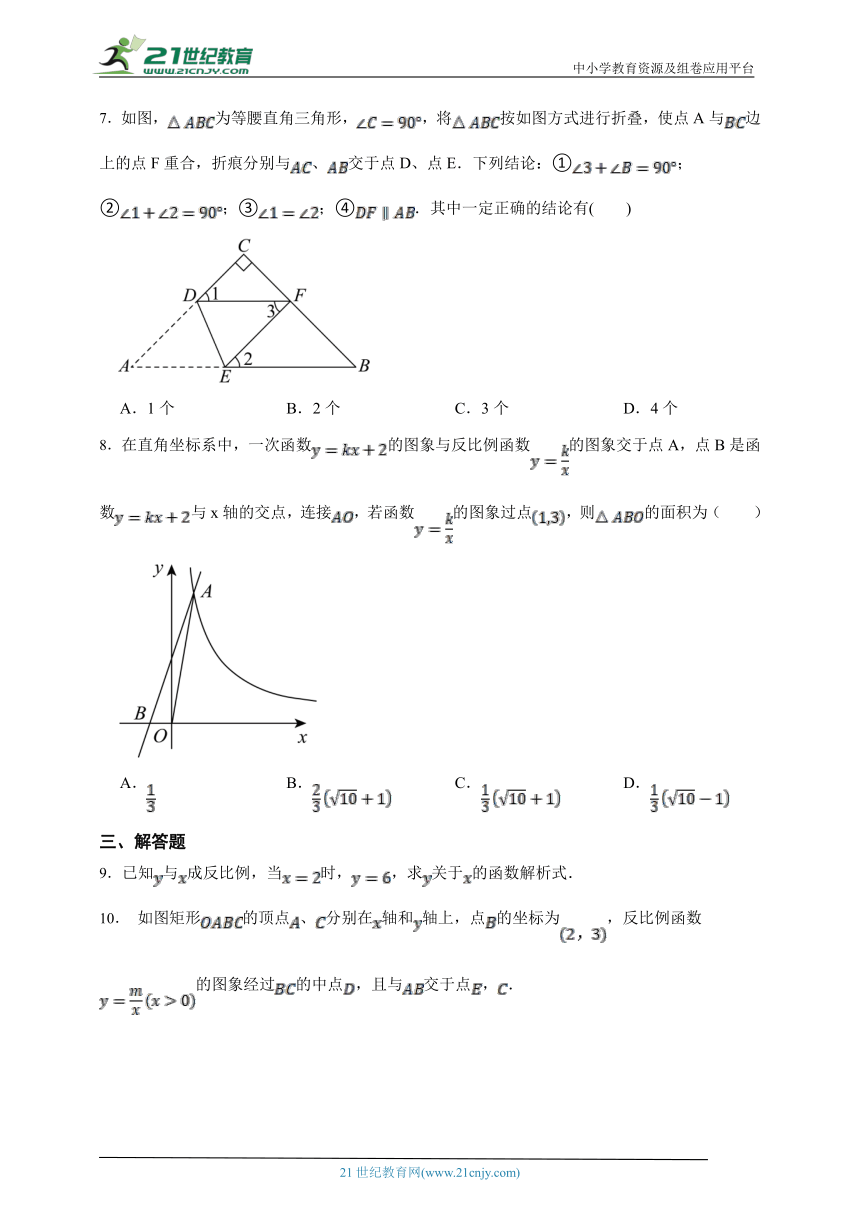
4.在同一平面直角坐标系中,一次函数与反比例函数的图象可能是( )
A. B.
C. D.
5.如图,一次函数y =ax+b(a≠0)和反比例函数 y 的图象相交于 A,B两点,则使 y ≤y 成立的x的取值范围是 ( )
A.-2≤x≤0或0≤x≤4 B.x≤-2或0C.-2≤x<0或x≥4 D.-2≤x≤0或x≥4
6. 如图①,区间测速是指检测机动车在两个相邻测速监控点之间的路段(测速区间)上平均速度的方法.小聪发现安全驾驶且不超过限速的条件下,汽车在某一高速路的限速区间段的平均行驶速度与行驶时间是反比例函数关系(如图②),已知高速公路上行驶的小型载客汽车最高车速不得超过,最低车速不得低于,小聪的爸爸按照此规定通过该限速区间段的时间可能是( )
A. B. C. D.
7.如图,为等腰直角三角形,,将按如图方式进行折叠,使点A与边上的点F重合,折痕分别与、交于点D、点E.下列结论:①;②;③;④.其中一定正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.在直角坐标系中,一次函数的图象与反比例函数的图象交于点A,点B是函数与x轴的交点,连接,若函数的图象过点,则的面积为( )
A. B. C. D.
三、解答题
9.已知与成反比例,当时,,求关于的函数解析式.
10. 如图矩形的顶点、分别在轴和轴上,点的坐标为,反比例函数的图象经过的中点,且与交于点,.
(1)求反比例函数的表达式及点的坐标.
(2)若点是边上的一点,且为等腰三角形,求直线的表达式.
11.已知一次函数与反比例函数的图象相交于点和点.
(1)试确定一次函数与反比例函数的表达式;
(2)若点P在x轴上,且的面积为,求点P的坐标;
(3)结合图象直接写出不等式的解集.
四、计算题
12.计算:.
五、综合题
13.一种树苗的高度用h表示,树苗生长的年数用a表示,测得的有关数据如下表:(树苗原高100 cm)
年数a 高度h/cm
1 100+5
2 100+10
3 100+15
4 100+20
… …
(1)试用年数a的代数式表示h;
(2)此树苗需多少年就可长到200cm高
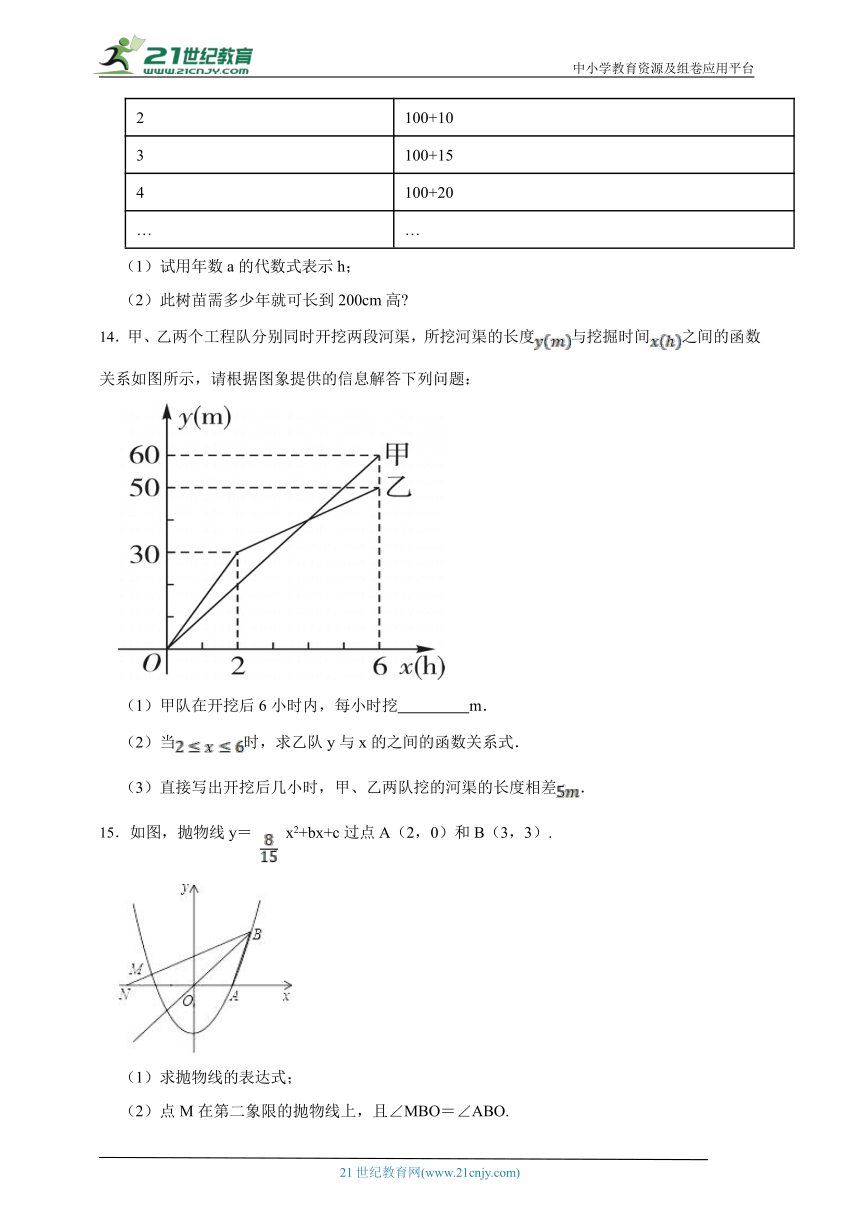
14.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度与挖掘时间之间的函数关系如图所示,请根据图象提供的信息解答下列问题:
(1)甲队在开挖后6小时内,每小时挖 m.
(2)当时,求乙队y与x的之间的函数关系式.
(3)直接写出开挖后几小时,甲、乙两队挖的河渠的长度相差.
15.如图,抛物线y= x2+bx+c过点A(2,0)和B(3,3).
(1)求抛物线的表达式;
(2)点M在第二象限的抛物线上,且∠MBO=∠ABO.
①直线BM交x轴于点N,求线段ON的长;
②延长BO交抛物线于点C,点P是平面内一点,连接PC、OP,当△POC∽△MOB时,请直接写出点P的坐标.
六、实践探究题
16.【背景】在一次物理实验中,小冉同学用一个固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R,RL之间关系为,通过实验得出如下数据:
R(Ω) … 1 a 3 4 6 …
I(A) … 4 3 2.4 2 b …
(1)a= ,b= .
(2)【探究】根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质.
①在平面直角坐标系中画出对应函数的图象.
②随着自变量的不断增大,函数值的变化趋势是 ▲ .
(3)【拓展】结合(2)中函数图象分析,当0时,的解为 .
17.视力表中蕴含着很多数学知识,如:每个“”形图都是正方形结构,同一行的“”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
素材1 国际通用的视力表以5米为检测距离,任选视力表中7个视力值n,测得对应行的“”形图边长b(mm),在平面直角坐标系中描点如图1.探究1 检测距离为5米时,归纳n与b的关系式,并求视力值1.2所对应行的“”形图边长.
素材2 图2为视网膜成像示意图,在检测视力时,眼睛能看清最小“”形图所成的角叫做分辨视角θ.视力值n与分辨视角θ(分)的对应关系近似满足n=(0.5≤θ≤10).探究2 当n≥1.0时,属于正常视力,根据函数增减性写出对应的分辨视角θ的范围.
素材3 如图3,当θ确定时,在A处用边长为b1的Ⅰ号“”测得的视力与在B处用边长为b2的Ⅱ号“”测得的视力相同.探究3 若检测距离为3米,求视力值1.2所对应行的“”形图边长.
18. 【问题探究】
课外兴趣小组活动时,同学们正在解决如下问题:
如图1,在矩形ABCD中,点E,F分别是边DC,BC上的点,连接AE,DF,且于点G,若,,求的值.
(1)请你帮助同学们解决上述问题,并说明理由.
(2)【初步运用】
如图2,在△ABC中,,点D为AC的中点,连接BD,过点A作于点点E,交BC于点F,求的值.
(3)【灵活运用】
如图3,在四边形ABCD中,,,,,点E,F分别在边AB,AD上,且,垂足为G,则 .
答案解析部分
1.【答案】
【知识点】勾股定理;正方形的性质;翻折变换(折叠问题)
2.【答案】112.5°
【知识点】三角形内角和定理;多边形内角与外角;矩形的性质;翻折变换(折叠问题);矩形翻折模型
3.【答案】2
【知识点】圆周角定理;切线的判定与性质;相似三角形的判定与性质
4.【答案】C
【知识点】反比例函数与一次函数的交点问题
5.【答案】C
【知识点】反比例函数与一次函数的交点问题
6.【答案】B
【知识点】反比例函数的实际应用
7.【答案】B
【知识点】平行线的判定与性质;三角形内角和定理;翻折变换(折叠问题)
8.【答案】C
【知识点】反比例函数与一次函数的交点问题
9.【答案】
【知识点】待定系数法求反比例函数解析式
10.【答案】(1)解:点的坐标为,点是的中点,
,
点在反比例函数上,
,
解得:,
反比例函数的解析式为.
四边形是矩形,点的坐标为,
当时,,
点坐标为;
(2)解:为等腰三角形,
,
点的坐标为,
,
设直线的解析式为,
,
解得:,
直线的解析式为.
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;等腰三角形的性质
11.【答案】(1),;
(2)点P的坐标为;
(3)或.
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
12.【答案】解:原式.
【知识点】实数的运算
13.【答案】(1)解:由表可知h=100+5a,
(2)解:当h=200 cm时,有200=100+5a,解得a=20,
答:此树苗需20年就可长到200cm高.
【知识点】一次函数的实际应用
14.【答案】(1)10
(2)解:设乙队在的时段内与x之间的函数关系式为:,
由图可知,函数图象过点、,
,
解得,
;
(3)解:开挖后或或,甲、乙两队挖的河渠的长度相差.
【知识点】待定系数法求一次函数解析式;一次函数的实际应用;通过函数图象获取信息并解决问题
15.【答案】(1)解:把点A、B坐标代入二次函数表达式:
,解得: ,
故:抛物线的表达式为: ……①;
(2)解:①过点B分别向x轴、y轴作垂线,交于点S、K,连接A、L,
点B坐标为(3,3)则:四边形OSBK为正方形,
∵∠MBO=∠ABO,BO是正方形OSBK的对角线,BO=BO,
∴△BOL≌△BOA(AAS),
∴OA=OL=2,∴AL⊥BO,
sinα= = = ,则cosα= ,tanα= ,
∵OL∥BS,∴ ,即: ,
则:ON=6;
②则点N坐标为(﹣6,0),
把点L(0,2)、N坐标代入一次函数表达式:y=kx+b,
解得:y= x+2…②,
联立①、②解得:x=﹣3或3(舍去3)
即点M坐标为(﹣3,1),
BC所在的直线的表达式为:y=x…③,
联立①、③解得:x=﹣ 或3(舍去3),
则点C坐标为(﹣ ,﹣ ),
则:OM= ,OB=3 ,OC= ,MB=2
当△POC∽△MOB时,点P的位置可能第二象限也可能在第四象限,
当点P在第二象限时,如下图,过点P作PH⊥x轴,
△POC∽△MOB,∠PCO=∠MBO=α,
∴ = = ,即: = ,
解得:OP= ,PC═ ,
AB所在直线表达式中的k值为3,
∵∠PCO=∠MBO=∠OBA=α,
∴PC所在直线表达式中的k值为3,
则:PC所在的直线表达式为:y=3x+ ,
令y=0,则x=﹣ ,
即Q点坐标为(﹣ ,0),即:OQ= ,
则:CQ= ,则:PQ=PC﹣CQ,
而PH2=OP2﹣OH2=PQ2﹣QH2=PQ2﹣(OQ﹣OH)2,
其中,OP= ,PQ=PC﹣CQ,OQ= ,
解得:OH= ,
则点P坐标为(﹣ , ),
当点P在第四象限时,同理可求点P坐标为 ,
故点P坐标为 或 .
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-几何问题
16.【答案】(1)2;1.5
(2)解:①根据表格数据描点:,,,,,在平面直角坐标系中画出对应函数的图象如下:
②不断减小
(3)或
【知识点】反比例函数与一次函数的交点问题;反比例函数的实际应用
17.【答案】解:探究1:
由图象中的点的坐标规律得到n与b成反比例关系,
设,
将其中一点(9,0.8)代入得:,
解得:k=7.2,
∴,
将其余各点一一代入验证,都符合关系式;
将 n=1.2 代入n=得:b=6;
答:检测距离为5米时, n与b的关系式为,且视力值1.2所对应行的“E”形图边长为6mm,视力值1.2所对应行的“E”形图边长为6mm;
探究2:
∵,
∴在自变量θ的取值范围内,n随着θ的增大而减小,
∴当n≥1.0时,0<θ≤1.0,
∵θ的取值范围是:0.5≤θ≤10,
∴0.5≤θ≤1.0;
探究3:由素材可知,当某人的视力确定时,其分辨视角也是确定的,由相似三角形性质可得
由探究1知b1=6mm,
∴
解得,
答:检测距离为3m时,视力值1.2所对应行的“E”形图边长为.
【知识点】反比例函数的实际应用;相似三角形的应用
18.【答案】(1)解:四边形ABCD是矩形,且,
,,
,
,
,
,
;
(2)解:过点B作CB的垂线,过点D作BC的垂线,垂足为K,过点A作BC的平行线,分别交两条垂线于G、H,如图:
则四边形GBKH为矩形,
D为AC的中点,
,
,
,
,
,
,
,
,
,
,
,,
,
设,则,AG=3y,AH=
,
由(1)知:,
.
(3)
【知识点】矩形的判定与性质;相似三角形的判定与性质;三角形全等的判定-AAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【北师大版九上同步练习】
第六章反比例函数(培优)检测题
一、填空题
1.如图,正方形边长为6,点为边的中点,连接,将沿翻折得到,延长交于点,则长为 .
2.将一张长方形纸片ABCD(长方形的四个内角都是直角)按如图所示操作
①将DA沿DP向内折叠,使点A落在点A1处;
②将DP沿DA1向内继续折叠,使点P落在点P1处,折痕与边AB交于点M.若P1MAB,则∠DP1M的度数等于 .
3.如图,在边长为6的正方形内部存在一动点,且满足,连接,则的最大值是 .
二、单选题
4.在同一平面直角坐标系中,一次函数与反比例函数的图象可能是( )
A. B.
C. D.
5.如图,一次函数y =ax+b(a≠0)和反比例函数 y 的图象相交于 A,B两点,则使 y ≤y 成立的x的取值范围是 ( )
A.-2≤x≤0或0≤x≤4 B.x≤-2或0
6. 如图①,区间测速是指检测机动车在两个相邻测速监控点之间的路段(测速区间)上平均速度的方法.小聪发现安全驾驶且不超过限速的条件下,汽车在某一高速路的限速区间段的平均行驶速度与行驶时间是反比例函数关系(如图②),已知高速公路上行驶的小型载客汽车最高车速不得超过,最低车速不得低于,小聪的爸爸按照此规定通过该限速区间段的时间可能是( )
A. B. C. D.
7.如图,为等腰直角三角形,,将按如图方式进行折叠,使点A与边上的点F重合,折痕分别与、交于点D、点E.下列结论:①;②;③;④.其中一定正确的结论有( )
A.1个 B.2个 C.3个 D.4个
8.在直角坐标系中,一次函数的图象与反比例函数的图象交于点A,点B是函数与x轴的交点,连接,若函数的图象过点,则的面积为( )
A. B. C. D.
三、解答题
9.已知与成反比例,当时,,求关于的函数解析式.
10. 如图矩形的顶点、分别在轴和轴上,点的坐标为,反比例函数的图象经过的中点,且与交于点,.
(1)求反比例函数的表达式及点的坐标.
(2)若点是边上的一点,且为等腰三角形,求直线的表达式.
11.已知一次函数与反比例函数的图象相交于点和点.
(1)试确定一次函数与反比例函数的表达式;
(2)若点P在x轴上,且的面积为,求点P的坐标;
(3)结合图象直接写出不等式的解集.
四、计算题
12.计算:.
五、综合题
13.一种树苗的高度用h表示,树苗生长的年数用a表示,测得的有关数据如下表:(树苗原高100 cm)
年数a 高度h/cm
1 100+5
2 100+10
3 100+15
4 100+20
… …
(1)试用年数a的代数式表示h;
(2)此树苗需多少年就可长到200cm高
14.甲、乙两个工程队分别同时开挖两段河渠,所挖河渠的长度与挖掘时间之间的函数关系如图所示,请根据图象提供的信息解答下列问题:
(1)甲队在开挖后6小时内,每小时挖 m.
(2)当时,求乙队y与x的之间的函数关系式.
(3)直接写出开挖后几小时,甲、乙两队挖的河渠的长度相差.
15.如图,抛物线y= x2+bx+c过点A(2,0)和B(3,3).
(1)求抛物线的表达式;
(2)点M在第二象限的抛物线上,且∠MBO=∠ABO.
①直线BM交x轴于点N,求线段ON的长;
②延长BO交抛物线于点C,点P是平面内一点,连接PC、OP,当△POC∽△MOB时,请直接写出点P的坐标.
六、实践探究题
16.【背景】在一次物理实验中,小冉同学用一个固定电压为12V的蓄电池,通过调节滑动变阻器来改变电流大小,完成控制灯泡L(灯丝的阻值RL=2Ω)亮度的实验(如图),已知串联电路中,电流与电阻R,RL之间关系为,通过实验得出如下数据:
R(Ω) … 1 a 3 4 6 …
I(A) … 4 3 2.4 2 b …
(1)a= ,b= .
(2)【探究】根据以上实验,构建出函数,结合表格信息,探究函数的图象与性质.
①在平面直角坐标系中画出对应函数的图象.
②随着自变量的不断增大,函数值的变化趋势是 ▲ .
(3)【拓展】结合(2)中函数图象分析,当0时,的解为 .
17.视力表中蕴含着很多数学知识,如:每个“”形图都是正方形结构,同一行的“”是全等图形且对应着同一个视力值,不同的检测距离需要不同的视力表.
素材1 国际通用的视力表以5米为检测距离,任选视力表中7个视力值n,测得对应行的“”形图边长b(mm),在平面直角坐标系中描点如图1.探究1 检测距离为5米时,归纳n与b的关系式,并求视力值1.2所对应行的“”形图边长.
素材2 图2为视网膜成像示意图,在检测视力时,眼睛能看清最小“”形图所成的角叫做分辨视角θ.视力值n与分辨视角θ(分)的对应关系近似满足n=(0.5≤θ≤10).探究2 当n≥1.0时,属于正常视力,根据函数增减性写出对应的分辨视角θ的范围.
素材3 如图3,当θ确定时,在A处用边长为b1的Ⅰ号“”测得的视力与在B处用边长为b2的Ⅱ号“”测得的视力相同.探究3 若检测距离为3米,求视力值1.2所对应行的“”形图边长.
18. 【问题探究】
课外兴趣小组活动时,同学们正在解决如下问题:
如图1,在矩形ABCD中,点E,F分别是边DC,BC上的点,连接AE,DF,且于点G,若,,求的值.
(1)请你帮助同学们解决上述问题,并说明理由.
(2)【初步运用】
如图2,在△ABC中,,点D为AC的中点,连接BD,过点A作于点点E,交BC于点F,求的值.
(3)【灵活运用】
如图3,在四边形ABCD中,,,,,点E,F分别在边AB,AD上,且,垂足为G,则 .
答案解析部分
1.【答案】
【知识点】勾股定理;正方形的性质;翻折变换(折叠问题)
2.【答案】112.5°
【知识点】三角形内角和定理;多边形内角与外角;矩形的性质;翻折变换(折叠问题);矩形翻折模型
3.【答案】2
【知识点】圆周角定理;切线的判定与性质;相似三角形的判定与性质
4.【答案】C
【知识点】反比例函数与一次函数的交点问题
5.【答案】C
【知识点】反比例函数与一次函数的交点问题
6.【答案】B
【知识点】反比例函数的实际应用
7.【答案】B
【知识点】平行线的判定与性质;三角形内角和定理;翻折变换(折叠问题)
8.【答案】C
【知识点】反比例函数与一次函数的交点问题
9.【答案】
【知识点】待定系数法求反比例函数解析式
10.【答案】(1)解:点的坐标为,点是的中点,
,
点在反比例函数上,
,
解得:,
反比例函数的解析式为.
四边形是矩形,点的坐标为,
当时,,
点坐标为;
(2)解:为等腰三角形,
,
点的坐标为,
,
设直线的解析式为,
,
解得:,
直线的解析式为.
【知识点】待定系数法求一次函数解析式;反比例函数与一次函数的交点问题;等腰三角形的性质
11.【答案】(1),;
(2)点P的坐标为;
(3)或.
【知识点】待定系数法求一次函数解析式;待定系数法求反比例函数解析式;反比例函数与一次函数的交点问题
12.【答案】解:原式.
【知识点】实数的运算
13.【答案】(1)解:由表可知h=100+5a,
(2)解:当h=200 cm时,有200=100+5a,解得a=20,
答:此树苗需20年就可长到200cm高.
【知识点】一次函数的实际应用
14.【答案】(1)10
(2)解:设乙队在的时段内与x之间的函数关系式为:,
由图可知,函数图象过点、,
,
解得,
;
(3)解:开挖后或或,甲、乙两队挖的河渠的长度相差.
【知识点】待定系数法求一次函数解析式;一次函数的实际应用;通过函数图象获取信息并解决问题
15.【答案】(1)解:把点A、B坐标代入二次函数表达式:
,解得: ,
故:抛物线的表达式为: ……①;
(2)解:①过点B分别向x轴、y轴作垂线,交于点S、K,连接A、L,
点B坐标为(3,3)则:四边形OSBK为正方形,
∵∠MBO=∠ABO,BO是正方形OSBK的对角线,BO=BO,
∴△BOL≌△BOA(AAS),
∴OA=OL=2,∴AL⊥BO,
sinα= = = ,则cosα= ,tanα= ,
∵OL∥BS,∴ ,即: ,
则:ON=6;
②则点N坐标为(﹣6,0),
把点L(0,2)、N坐标代入一次函数表达式:y=kx+b,
解得:y= x+2…②,
联立①、②解得:x=﹣3或3(舍去3)
即点M坐标为(﹣3,1),
BC所在的直线的表达式为:y=x…③,
联立①、③解得:x=﹣ 或3(舍去3),
则点C坐标为(﹣ ,﹣ ),
则:OM= ,OB=3 ,OC= ,MB=2
当△POC∽△MOB时,点P的位置可能第二象限也可能在第四象限,
当点P在第二象限时,如下图,过点P作PH⊥x轴,
△POC∽△MOB,∠PCO=∠MBO=α,
∴ = = ,即: = ,
解得:OP= ,PC═ ,
AB所在直线表达式中的k值为3,
∵∠PCO=∠MBO=∠OBA=α,
∴PC所在直线表达式中的k值为3,
则:PC所在的直线表达式为:y=3x+ ,
令y=0,则x=﹣ ,
即Q点坐标为(﹣ ,0),即:OQ= ,
则:CQ= ,则:PQ=PC﹣CQ,
而PH2=OP2﹣OH2=PQ2﹣QH2=PQ2﹣(OQ﹣OH)2,
其中,OP= ,PQ=PC﹣CQ,OQ= ,
解得:OH= ,
则点P坐标为(﹣ , ),
当点P在第四象限时,同理可求点P坐标为 ,
故点P坐标为 或 .
【知识点】待定系数法求二次函数解析式;二次函数的实际应用-几何问题
16.【答案】(1)2;1.5
(2)解:①根据表格数据描点:,,,,,在平面直角坐标系中画出对应函数的图象如下:
②不断减小
(3)或
【知识点】反比例函数与一次函数的交点问题;反比例函数的实际应用
17.【答案】解:探究1:
由图象中的点的坐标规律得到n与b成反比例关系,
设,
将其中一点(9,0.8)代入得:,
解得:k=7.2,
∴,
将其余各点一一代入验证,都符合关系式;
将 n=1.2 代入n=得:b=6;
答:检测距离为5米时, n与b的关系式为,且视力值1.2所对应行的“E”形图边长为6mm,视力值1.2所对应行的“E”形图边长为6mm;
探究2:
∵,
∴在自变量θ的取值范围内,n随着θ的增大而减小,
∴当n≥1.0时,0<θ≤1.0,
∵θ的取值范围是:0.5≤θ≤10,
∴0.5≤θ≤1.0;
探究3:由素材可知,当某人的视力确定时,其分辨视角也是确定的,由相似三角形性质可得
由探究1知b1=6mm,
∴
解得,
答:检测距离为3m时,视力值1.2所对应行的“E”形图边长为.
【知识点】反比例函数的实际应用;相似三角形的应用
18.【答案】(1)解:四边形ABCD是矩形,且,
,,
,
,
,
,
;
(2)解:过点B作CB的垂线,过点D作BC的垂线,垂足为K,过点A作BC的平行线,分别交两条垂线于G、H,如图:
则四边形GBKH为矩形,
D为AC的中点,
,
,
,
,
,
,
,
,
,
,
,,
,
设,则,AG=3y,AH=
,
由(1)知:,
.
(3)
【知识点】矩形的判定与性质;相似三角形的判定与性质;三角形全等的判定-AAS
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
