2024年云南省昆明市第八中学初中学业水平检测(四)数学试卷(含答案)
文档属性
| 名称 | 2024年云南省昆明市第八中学初中学业水平检测(四)数学试卷(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 481.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 16:05:44 | ||
图片预览




文档简介
2024年云南省昆明市第八中学初中学业水平检测
数学模拟卷(四)
(全卷三个大题,共27个小题,共4页,满分100分,考试用时120分钟)
注意事项:
1.本卷为试题卷.考生必须在答题卡上解题作答。答案应书写在答题卡的相应位置上,在试题卷、草稿纸上作答无效.
2.考试结束后,请将试题卷和答题卡一并交回.
一、选择题(本大题共15小题,每小题只有一个正确选项,每小题2分,共30分)
1.《九章算术》中有注:“今两算得失相反,要令正负以名之.”意思就是:在计算过程中遇到具有相反意义的量,要用正数和负数来区分.如果室内温度为零上8℃,记为+8℃,那么室外温度为零下2℃,记为( )
A.-2℃ B.+2℃ C.-8℃ D.+8℃
2.如图,已知,AD,BC交于点O,若,则∠C的度数为( )
A.30° B.45° C.60° D.70°
3.据共青团中央2024年5月3日发布数据显示,截至2023年12月底,全国共有共青团员74167000名,数据74167000用科学记数法表示为( )
A. B. C. D.
4.如图所示,是一个简单几何体的三视图,该几何体是( )
A.三棱柱 B.三棱锥 C.圆柱 D.圆锥
5.下列运算正确的是( )
A. B. C. D.
6.若反比例函数的图象经过点(-2,3),则k的值为( )
A.-2 B.-6 C.5 D.3
7.下列图形不是轴对称图形的是( )
A. B. C. D.
8.按一定规律排列的单项式:,第个单项式是( )
A. B. C. D.
9.在第75个“五四”青年节到来之际,共青团云南省直机关工作委员会启动2024年云南省直机关“奋斗正青春 筑梦新时代”青年主题活动以及青年文明号开放周,在青年文明号开放周期间,各省直单位面向广大群众,特别是青年群体,开展岗位体验、实地观摩、文化倡导、政策宣传、公益服务等实践活动,团结引领广大青年听党话、跟党走,奋进新征程、建功新时代.某校部分团员参加青年文明号开放周实践活动人数的条形统计图和扇形统计图(每人只参加一项)如图所示,则参加“公益服务”的团员人数是( )
A.80人 B.100人 C.120人 D.140人
10.如图,点A,B,C在上,若,则∠BOC的度数为( )
A.70° B110° C.130° D.140°
11.如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,连接AE,若BC=8,EC=3,则AE的长是( )
A.11 B.8 C.5 D.3
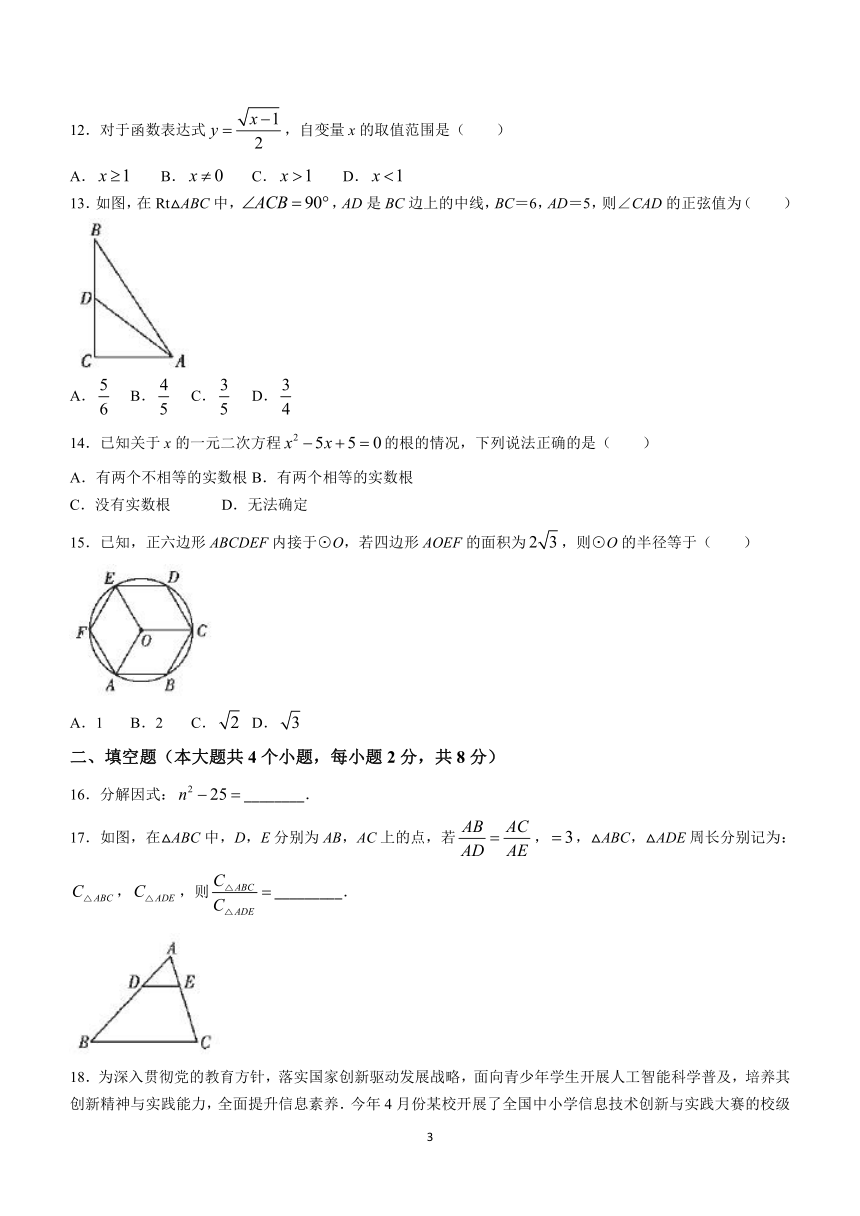
12.对于函数表达式,自变量x的取值范围是( )
A. B. C. D.
13.如图,在Rt△ABC中,,AD是BC边上的中线,BC=6,AD=5,则∠CAD的正弦值为( )
A. B. C. D.
14.已知关于x的一元二次方程的根的情况,下列说法正确的是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
15.已知,正六边形ABCDEF内接于⊙O,若四边形AOEF的面积为,则⊙O的半径等于( )
A.1 B.2 C. D.
二、填空题(本大题共4个小题,每小题2分,共8分)
16.分解因式:________.
17.如图,在△ABC中,D,E分别为AB,AC上的点,若,,△ABC,△ADE周长分别记为:,,则_________.
18.为深入贯彻党的教育方针,落实国家创新驱动发展战略,面向青少年学生开展人工智能科学普及,培养其创新精神与实践能力,全面提升信息素养.今年4月份某校开展了全国中小学信息技术创新与实践大赛的校级选拔赛.经过几轮筛选,学校决定从甲、乙、丙、丁四名同学中选择一名同学代表学校参加本次比赛,经过统计,四名同学成绩的平均数(单位:分)及方差(单位:分2)如表所示:
甲 乙 丙 丁
平均数 92.5 95 92.5 95
方差 6.25 8.33 22.92 29.17
若要选一名成绩好且状态稳定的同学参赛,那么应该选择_______.
19.已知圆锥底面圆直径是8,圆锥的母线长为6,则这个圆锥的侧面积是_______.
三、解答题(本大题共8个小题,共62分)
20.(本小题满分7分)计算:.
21.(本小题满分6分)如图,C,D是AF上的两点,且AB=DE,AC=DF,BC=EF.
求证:∠B=∠E.
22.(本小题满分7分)悠悠艾草香,片片粽叶长;一年一端午,一岁一安康.端午节吃粽子是华夏民族的传统习俗.某超市购进了甲、乙两种口味的粽子,已知每个甲种粽子的价格比每个乙种粽子的价格多3元,且用240元购进甲种粽子的个数与用180元购进乙种粽子的个数相同.求乙种粽子的单价是多少元?
23.(本小题满分6分)2024年4月22日,为迎接第九个“中国航天日”,“逐梦星汉,探索苍穹——2024中国航天日云南航天科普教育系列活动”在昆明市盘龙区启幕,相关部门干部职工以及部分学生,通过参加开幕式、现场聆听院士讲座等方式,了解我国航天科技的发展,在参加活动前,某班接到通知,在聆听院士讲座后,推荐一名学生与院士互动交流,班主任决定通过抽牌游戏从李昆和张明两人中选出一人参加现场互动交流,游戏规则:李昆从背面完全相同,正面分别是黑桃2、黑桃3、黑桃4和黑桃5的四张扑克牌中随机抽一张,不放回.然后张明再从剩余三张扑克牌中随机抽一张,如果两次所抽出的数字之和为奇数,那么李星与院士交流互动,否则张明与院士交流互动.
(1)用列表或画树状图的方法,列出李昆和张明两次抽牌得数字的所有可能情况;
(2)请判断这个游戏是否公平,并说明现由。
24.(本小题满分8分)如图,在△ABC中,AB=AC,M,O分别为边BC,AC中点,延长MO至点D,使OD=OM,连接AD,CD.
(1)求证:四边形AMCD是矩形;
(2)若四边形AMCD的面积为6,,求矩形AMCD的周长.
25.(本小题满分8分)一年一度的校园文化节开始了,某班艺术节目需要在淘宝上采购甲、乙两种道具,一商家对甲种道具的出售价格根据购买量给予优惠,对乙种道具按40元/件的价格出售,设该班购买甲种道具件,付款y元,y与x之间的函数关系如图所示:
(1)求y与x的函数解析式;
(2)若该班计划一次性购买甲、乙两种道具共100件,且甲种道具数量不少于乙种道具数量的,甲种道具不超过75件,如何分配甲、乙两种道具的购进量,才能使该班付款总金额(元)最少?
26.(本小融满分8分)在平面直角坐标系xOy中,已知抛物线过定点(2,-1).
(1)求抛物线的对称轴;
(2)求的值.
27.(本小题满分12分)如图,已知AB为的直径,F为上一点,AC平分∠BAF且交于点C,过点C作于点D,延长AB,DC交于点E,连接BC,CF.
(1)若BC=5,AC=12,求的半径;
(2)求证:CD是的切线;
(3)是否存在常数,使得,若存在,求出的值,若不存在,请说明理由。
2024年云南省昆明市第八中学初中学业水平检测(四)--数学
参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案 A C A D D B B D C D C A C A B
16. 17.3 18.乙 19.
20.解:原式.
21.证明:在△ABC和△DEF中,
,∴,∴.
22.解:设乙种粽子的单价是x元,则甲种粽子的单价为(x+3)元.
依意得:
解得:x=9.
经检验,x=9是原分式方程的解,且符合题意.
答:乙种粽子的单价是9元.
23.解:(1)列表分析如下:
李昆抽张明抽 2 3 4 5
2 (3,2) (4,2) (5,2)
3 (2,3) (4,3) (5,3)
4 (2,4) (3,4) (5,4)
5 (2,5) (3,5) (4,5)
共有(2,3)、(2,4)、(2,5)、(3,2)、(3,4)、(3,5)、(4,2)、(4,3)、(4,5)、(5,2)、(5,3)、(5,4)这12种等可能结果;
或画树状图如下:
共有(2,3)、(2,4)、(2,5)、(3,2)、(3,4)、(3,5)、(4,2),(4,3)、(4,5)、(5,2)、(5,3),(5,4)这12种等可能细果;
(2)这个游戏不公平,理由如下:
由表或图可以看出,所有可能的结果共有12种,这些结果出现的可能性相等.其中,两次抽扑克牌上的数字之和为奇数的有8种:(2,3)、(2,5)、(3,2)、(3,4)、(4,3)、(4,5)、(5,2)、(5,4).故李昆与院士交流互动的概率,张明与院士交流动的概率.
∵,∴这个游戏不公平.
24.(1)证明:∵O为AC中点,∴OA=OC.
∵OD=OM,∴四边形AMCD为平行四边形.
∵AB=AC,∴△ABC为等腰三角形,
∵M为BC边中点,∴
∴∠AMC=90°,∴四边形AMCD为矩形.
(2)解:设AM=a,MC=b,
∵矩形AMCD的面积为6,∴
∵,且∠AMC=90°,
∴在Rt△AMC中,由勾股定理得
即
∵,∴,即.
∵,.
∴矩形AMCD的周长为.
25.解:(1)当时,设函数解析式为,
把点(60,2400)代入得:,解得:.
∴当时,设函数解析式为.
当时,函数解析式为,
把点(60,2400),(80,2600)代入得:
,解得:
∴当时,.
综上所述y与x的函数解析式为;
(2)设购进甲种道具a件,则购进乙种道具(100-a)件,
由题知,,解得:.
当时,
;
,随a的增大而减小,
当a=75时,(元).
即当a=75时,付款总金额最少,最少付款总金额为3550元.
此时乙种道具为(件).
答:购进甲种道具75件,乙种道具25件,才能使该班付款总金额最少.
26.解:(1)抛物线的对称轴为直线
∴抛物线的对称轴为直线;
(2)将定点(2,-1)代入抛物线解析式中,
得,∴,即.
,
,
.
27.(1)解:∵AB为⊙O的直径,∴∠ACB=90,
∵BC=5,AC=12,在Rt△ACB中,由勾股定理可得:
∴,
,故的半径长为;
(2)证明:如图连接OC
AB为⊙O的直径,,
,
,
平分∠BAF,,
,
,
是⊙O的半径,是⊙O的切线;
(3)存在,且k的值为2;
过点C作于点G,
在△ACG与△ACD中,
,,
,
平分∠BAF,.
,.
在Rt△BCG与Rt△FCD中,
,,
,
即.
数学模拟卷(四)
(全卷三个大题,共27个小题,共4页,满分100分,考试用时120分钟)
注意事项:
1.本卷为试题卷.考生必须在答题卡上解题作答。答案应书写在答题卡的相应位置上,在试题卷、草稿纸上作答无效.
2.考试结束后,请将试题卷和答题卡一并交回.
一、选择题(本大题共15小题,每小题只有一个正确选项,每小题2分,共30分)
1.《九章算术》中有注:“今两算得失相反,要令正负以名之.”意思就是:在计算过程中遇到具有相反意义的量,要用正数和负数来区分.如果室内温度为零上8℃,记为+8℃,那么室外温度为零下2℃,记为( )
A.-2℃ B.+2℃ C.-8℃ D.+8℃
2.如图,已知,AD,BC交于点O,若,则∠C的度数为( )
A.30° B.45° C.60° D.70°
3.据共青团中央2024年5月3日发布数据显示,截至2023年12月底,全国共有共青团员74167000名,数据74167000用科学记数法表示为( )
A. B. C. D.
4.如图所示,是一个简单几何体的三视图,该几何体是( )
A.三棱柱 B.三棱锥 C.圆柱 D.圆锥
5.下列运算正确的是( )
A. B. C. D.
6.若反比例函数的图象经过点(-2,3),则k的值为( )
A.-2 B.-6 C.5 D.3
7.下列图形不是轴对称图形的是( )
A. B. C. D.
8.按一定规律排列的单项式:,第个单项式是( )
A. B. C. D.
9.在第75个“五四”青年节到来之际,共青团云南省直机关工作委员会启动2024年云南省直机关“奋斗正青春 筑梦新时代”青年主题活动以及青年文明号开放周,在青年文明号开放周期间,各省直单位面向广大群众,特别是青年群体,开展岗位体验、实地观摩、文化倡导、政策宣传、公益服务等实践活动,团结引领广大青年听党话、跟党走,奋进新征程、建功新时代.某校部分团员参加青年文明号开放周实践活动人数的条形统计图和扇形统计图(每人只参加一项)如图所示,则参加“公益服务”的团员人数是( )
A.80人 B.100人 C.120人 D.140人
10.如图,点A,B,C在上,若,则∠BOC的度数为( )
A.70° B110° C.130° D.140°
11.如图,在△ABC中,AB的垂直平分线分别交AB,BC于点D,E,连接AE,若BC=8,EC=3,则AE的长是( )
A.11 B.8 C.5 D.3
12.对于函数表达式,自变量x的取值范围是( )
A. B. C. D.
13.如图,在Rt△ABC中,,AD是BC边上的中线,BC=6,AD=5,则∠CAD的正弦值为( )
A. B. C. D.
14.已知关于x的一元二次方程的根的情况,下列说法正确的是( )
A.有两个不相等的实数根 B.有两个相等的实数根
C.没有实数根 D.无法确定
15.已知,正六边形ABCDEF内接于⊙O,若四边形AOEF的面积为,则⊙O的半径等于( )
A.1 B.2 C. D.
二、填空题(本大题共4个小题,每小题2分,共8分)
16.分解因式:________.
17.如图,在△ABC中,D,E分别为AB,AC上的点,若,,△ABC,△ADE周长分别记为:,,则_________.
18.为深入贯彻党的教育方针,落实国家创新驱动发展战略,面向青少年学生开展人工智能科学普及,培养其创新精神与实践能力,全面提升信息素养.今年4月份某校开展了全国中小学信息技术创新与实践大赛的校级选拔赛.经过几轮筛选,学校决定从甲、乙、丙、丁四名同学中选择一名同学代表学校参加本次比赛,经过统计,四名同学成绩的平均数(单位:分)及方差(单位:分2)如表所示:
甲 乙 丙 丁
平均数 92.5 95 92.5 95
方差 6.25 8.33 22.92 29.17
若要选一名成绩好且状态稳定的同学参赛,那么应该选择_______.
19.已知圆锥底面圆直径是8,圆锥的母线长为6,则这个圆锥的侧面积是_______.
三、解答题(本大题共8个小题,共62分)
20.(本小题满分7分)计算:.
21.(本小题满分6分)如图,C,D是AF上的两点,且AB=DE,AC=DF,BC=EF.
求证:∠B=∠E.
22.(本小题满分7分)悠悠艾草香,片片粽叶长;一年一端午,一岁一安康.端午节吃粽子是华夏民族的传统习俗.某超市购进了甲、乙两种口味的粽子,已知每个甲种粽子的价格比每个乙种粽子的价格多3元,且用240元购进甲种粽子的个数与用180元购进乙种粽子的个数相同.求乙种粽子的单价是多少元?
23.(本小题满分6分)2024年4月22日,为迎接第九个“中国航天日”,“逐梦星汉,探索苍穹——2024中国航天日云南航天科普教育系列活动”在昆明市盘龙区启幕,相关部门干部职工以及部分学生,通过参加开幕式、现场聆听院士讲座等方式,了解我国航天科技的发展,在参加活动前,某班接到通知,在聆听院士讲座后,推荐一名学生与院士互动交流,班主任决定通过抽牌游戏从李昆和张明两人中选出一人参加现场互动交流,游戏规则:李昆从背面完全相同,正面分别是黑桃2、黑桃3、黑桃4和黑桃5的四张扑克牌中随机抽一张,不放回.然后张明再从剩余三张扑克牌中随机抽一张,如果两次所抽出的数字之和为奇数,那么李星与院士交流互动,否则张明与院士交流互动.
(1)用列表或画树状图的方法,列出李昆和张明两次抽牌得数字的所有可能情况;
(2)请判断这个游戏是否公平,并说明现由。
24.(本小题满分8分)如图,在△ABC中,AB=AC,M,O分别为边BC,AC中点,延长MO至点D,使OD=OM,连接AD,CD.
(1)求证:四边形AMCD是矩形;
(2)若四边形AMCD的面积为6,,求矩形AMCD的周长.
25.(本小题满分8分)一年一度的校园文化节开始了,某班艺术节目需要在淘宝上采购甲、乙两种道具,一商家对甲种道具的出售价格根据购买量给予优惠,对乙种道具按40元/件的价格出售,设该班购买甲种道具件,付款y元,y与x之间的函数关系如图所示:
(1)求y与x的函数解析式;
(2)若该班计划一次性购买甲、乙两种道具共100件,且甲种道具数量不少于乙种道具数量的,甲种道具不超过75件,如何分配甲、乙两种道具的购进量,才能使该班付款总金额(元)最少?
26.(本小融满分8分)在平面直角坐标系xOy中,已知抛物线过定点(2,-1).
(1)求抛物线的对称轴;
(2)求的值.
27.(本小题满分12分)如图,已知AB为的直径,F为上一点,AC平分∠BAF且交于点C,过点C作于点D,延长AB,DC交于点E,连接BC,CF.
(1)若BC=5,AC=12,求的半径;
(2)求证:CD是的切线;
(3)是否存在常数,使得,若存在,求出的值,若不存在,请说明理由。
2024年云南省昆明市第八中学初中学业水平检测(四)--数学
参考答案
题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
答案 A C A D D B B D C D C A C A B
16. 17.3 18.乙 19.
20.解:原式.
21.证明:在△ABC和△DEF中,
,∴,∴.
22.解:设乙种粽子的单价是x元,则甲种粽子的单价为(x+3)元.
依意得:
解得:x=9.
经检验,x=9是原分式方程的解,且符合题意.
答:乙种粽子的单价是9元.
23.解:(1)列表分析如下:
李昆抽张明抽 2 3 4 5
2 (3,2) (4,2) (5,2)
3 (2,3) (4,3) (5,3)
4 (2,4) (3,4) (5,4)
5 (2,5) (3,5) (4,5)
共有(2,3)、(2,4)、(2,5)、(3,2)、(3,4)、(3,5)、(4,2)、(4,3)、(4,5)、(5,2)、(5,3)、(5,4)这12种等可能结果;
或画树状图如下:
共有(2,3)、(2,4)、(2,5)、(3,2)、(3,4)、(3,5)、(4,2),(4,3)、(4,5)、(5,2)、(5,3),(5,4)这12种等可能细果;
(2)这个游戏不公平,理由如下:
由表或图可以看出,所有可能的结果共有12种,这些结果出现的可能性相等.其中,两次抽扑克牌上的数字之和为奇数的有8种:(2,3)、(2,5)、(3,2)、(3,4)、(4,3)、(4,5)、(5,2)、(5,4).故李昆与院士交流互动的概率,张明与院士交流动的概率.
∵,∴这个游戏不公平.
24.(1)证明:∵O为AC中点,∴OA=OC.
∵OD=OM,∴四边形AMCD为平行四边形.
∵AB=AC,∴△ABC为等腰三角形,
∵M为BC边中点,∴
∴∠AMC=90°,∴四边形AMCD为矩形.
(2)解:设AM=a,MC=b,
∵矩形AMCD的面积为6,∴
∵,且∠AMC=90°,
∴在Rt△AMC中,由勾股定理得
即
∵,∴,即.
∵,.
∴矩形AMCD的周长为.
25.解:(1)当时,设函数解析式为,
把点(60,2400)代入得:,解得:.
∴当时,设函数解析式为.
当时,函数解析式为,
把点(60,2400),(80,2600)代入得:
,解得:
∴当时,.
综上所述y与x的函数解析式为;
(2)设购进甲种道具a件,则购进乙种道具(100-a)件,
由题知,,解得:.
当时,
;
,随a的增大而减小,
当a=75时,(元).
即当a=75时,付款总金额最少,最少付款总金额为3550元.
此时乙种道具为(件).
答:购进甲种道具75件,乙种道具25件,才能使该班付款总金额最少.
26.解:(1)抛物线的对称轴为直线
∴抛物线的对称轴为直线;
(2)将定点(2,-1)代入抛物线解析式中,
得,∴,即.
,
,
.
27.(1)解:∵AB为⊙O的直径,∴∠ACB=90,
∵BC=5,AC=12,在Rt△ACB中,由勾股定理可得:
∴,
,故的半径长为;
(2)证明:如图连接OC
AB为⊙O的直径,,
,
,
平分∠BAF,,
,
,
是⊙O的半径,是⊙O的切线;
(3)存在,且k的值为2;
过点C作于点G,
在△ACG与△ACD中,
,,
,
平分∠BAF,.
,.
在Rt△BCG与Rt△FCD中,
,,
,
即.
同课章节目录
