青岛版数学八年级下册6.3特殊的平行四边形同步练习(含答案)
文档属性
| 名称 | 青岛版数学八年级下册6.3特殊的平行四边形同步练习(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 572.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-13 18:01:29 | ||
图片预览

文档简介
6.3 特殊的平行四边形
一、单选题
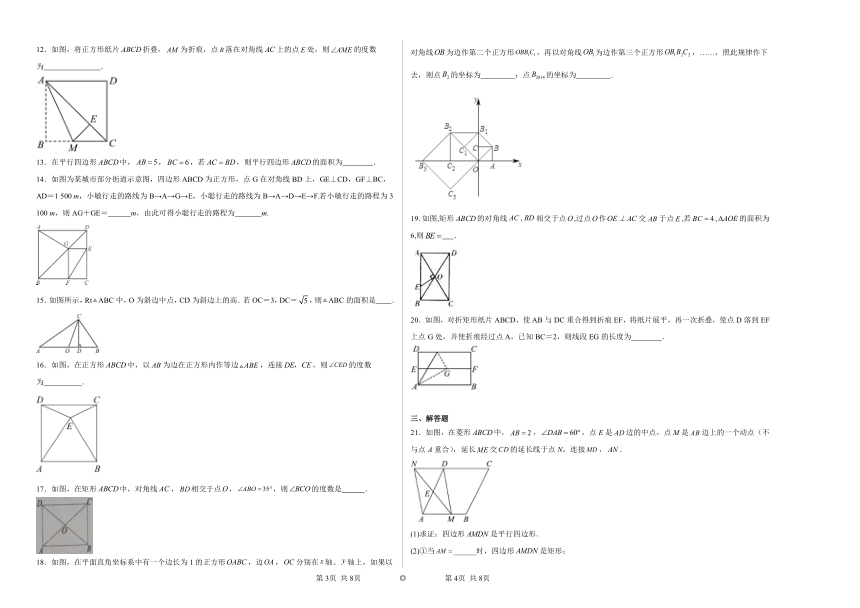
1.如图,在正方形ABCD中,AC、BD相交于点O,E、F分别在BC、CD上,BE=CF,AE、BF分别交BD、AC于M、N,连结OE、OF,下列结论:①AE=BF ②AE⊥BF;③OM=ON;④CE+CF=;其中正确的是( )
A.①③④ B.①② C.①②③④ D.①②③
2.已知菱形的面积为24,其中一条对角线长为8,则另一条对角线长为( )
A.3 B.4 C.5 D.6
3.对于四边形,给出下列组条件,①,;②,;③;④;⑤;⑥,.其中能得到“四边形是矩形”的条件有( )
A.组 B.组 C.组 D.组
4.如图,矩形ABCD中,对角线AC=8cm,△AOB是等边三角形,则AD的长为( )cm.
A.4 B.6 C.4 D.3
5.在菱形中,于点,于点,连结.若,则的度数为( )
A. B. C. D.
6.如图,菱形花坛的周长为,,沿着菱形的对角线修建两条小路和,则小路的长是( )
A. B. C. D.
7.如图,将长方形沿对角线折叠,点C落在点E处,交于点F,已知,则的度数为( )
A.32.5° B.25° C.50° D.65°
8.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )
A.3 B.12 C.6 D.4
9.取四边形的各边中点、、、,依次连接得到四边形,现知四边形是菱形,则四边形的对角线( )
A.相等 B.相等且平分
C.垂直 D.垂直且平分
10.如图,在矩形中,对角线,相交于点O,,,则的长是( )
A. B. C. D.
二、填空题
11.我们把依次连接任意一个四边形各边中点所得到的四边形叫做中点四边形.若一个四边形的中点四边形是一个矩形,则四边形可以是 .
12.如图,将正方形纸片折叠,为折痕,点落在对角线上的点处,则的度数为 .
13.在平行四边形中,,,若,则平行四边形的面积为 .
14.如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则AG+GE= m,由此可得小聪行走的路程为 m.
15.如图所示,RtABC中,O为斜边中点,CD为斜边上的高.若OC=3,DC=,则ABC的面积是 .
16.如图,在正方形中,以为边在正方形内作等边,连接,则的度数为 .
17.如图,在矩形中,对角线,相交于点,,则的度数是 .
18.如图,在平面直角坐标系中有一个边长为1的正方形,边,分别在轴、轴上,如果以对角线为边作第二个正方形,再以对角线为边作第三个正方形,……,照此规律作下去,则点的坐标为 ;点的坐标为 .
19.如图,矩形的对角线相交于点,过点作交于点,若,的面积为6,则 .
20.如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF上点G处,并使折痕经过点A,已知BC=2,则线段EG的长度为 .
三、解答题
21.如图,在菱形中,,,点E是边的中点,点M是边上的一个动点(不与点A重合),延长交的延长线于点N,连接,.
(1)求证:四边形是平行四边形.
(2)①当______时,四边形是矩形;
②当______时,四边形是菱形.
22.图1是“口子窖”酒的一个由铁皮制成的包装底盒,它是一个无盖的六棱柱形状的盒子(如图2),侧面是矩形或正方形.经测量,底面六边形有三条边的长是9,有三条边的长是3,每个内角都是,该六棱校的高为3.现沿它的侧棱剪开展平,得到如图3的平面展开图.
(1)制作这种底盒时,可以按图4中虚线裁剪出如图3的模片.现有一块长为17.5、宽为16.5的长方形铁皮,请问能否按图4的裁剪方法制作这样的无盖底盒?并请你说明理由;
(2)如果用一块正三角形铁皮按图5中虚线裁剪出如图3的模片,那么这个正三角形的边长至少应为 .(说明:以上裁剪均不计接缝处损耗.)
23.(1)如图1,在四边形中,,为上一点,连接,.
①若平分,平分,求的度数;
②若,,为中点,求证:为等腰直角三角形;
(2)某工程队需要在,两棵树的前方建立一座八角亭.按如下方法选址:如图2,甲工人从点直走到树处,然后向右转后再直走一段路等于的长度到点处;乙工人从点直走到树处,然后向左转后再直走一段路等于的长度到点处.工程队队长打算把八角亭建在的中点处.过几天,工程队带着建筑材料来施工,却发现忘记标记起始点,正当大家懊恼时,队长说:别急,只要找到,两棵树连线的中点,由点引的垂线,再往,两棵树前方量出的长度的一半,就能找到之前的点(如图3所示).你觉得队长的方法对吗?为什么?
24.进入世纪后,我国科技技术高速发展,很多行业领先于全球其他国家,物流快递行业就是其中之一,随着快递数量的暴增,某大型物流企业为提高效率,启用机器人分拣快递,在仓储中心有机器人的环形轨道,环形轨道是一个直角梯形(图①),且轨道和轨道在东西方向上,如图所示,,,,,,若机器人从点出发,搬运大件快递到点,运动速度是,机器人从点出发,搬运小件快递到点,然后返回点,运动速度是,假设两个机器人同时出发,机器人的运动时间是秒.
(1)在机器人从点到点的运动过程中,若用字母t表示下列线段长,则________,________;
(2)在机器人从点到点的运动过程中,当四边形是平行四边形时,求时间;
(3)从运动开始到机器人回到点的过程中,是否会出现机器P刚好在机器人的正北方向的时候,若存在,请算出机器人的运动时间,若不存在,请说明理由.
25.小兰的课桌桌面的形状如图所示,她想检查一下它是不是矩形,如果手头仅有一根比较长的绳子,请你帮她想一下应该如何做,并说明原因.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
2.D
3.D
4.C
5.D
6.A
7.C
8.C
9.A
10.A
11.正方形(答案不唯一,对角线互相垂直的四边形均可)
12.
13.
14. 1600 4600
15.
16.
17./55度
18.
19.
20.
21.(1)略 (2)①1;②2
22.(1)能,略 (2)
23.(1)①②略;(2)队长说法正确,略
24.(1),
(2)
(3)存在,机器刚好在机器人的正北方向的时候,的值为或
25.略
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,在正方形ABCD中,AC、BD相交于点O,E、F分别在BC、CD上,BE=CF,AE、BF分别交BD、AC于M、N,连结OE、OF,下列结论:①AE=BF ②AE⊥BF;③OM=ON;④CE+CF=;其中正确的是( )
A.①③④ B.①② C.①②③④ D.①②③
2.已知菱形的面积为24,其中一条对角线长为8,则另一条对角线长为( )
A.3 B.4 C.5 D.6
3.对于四边形,给出下列组条件,①,;②,;③;④;⑤;⑥,.其中能得到“四边形是矩形”的条件有( )
A.组 B.组 C.组 D.组
4.如图,矩形ABCD中,对角线AC=8cm,△AOB是等边三角形,则AD的长为( )cm.
A.4 B.6 C.4 D.3
5.在菱形中,于点,于点,连结.若,则的度数为( )
A. B. C. D.
6.如图,菱形花坛的周长为,,沿着菱形的对角线修建两条小路和,则小路的长是( )
A. B. C. D.
7.如图,将长方形沿对角线折叠,点C落在点E处,交于点F,已知,则的度数为( )
A.32.5° B.25° C.50° D.65°
8.如图,在矩形ABCD中,对角线AC,BD相交于点O,∠AOB=60°,AB=6,则AD=( )
A.3 B.12 C.6 D.4
9.取四边形的各边中点、、、,依次连接得到四边形,现知四边形是菱形,则四边形的对角线( )
A.相等 B.相等且平分
C.垂直 D.垂直且平分
10.如图,在矩形中,对角线,相交于点O,,,则的长是( )
A. B. C. D.
二、填空题
11.我们把依次连接任意一个四边形各边中点所得到的四边形叫做中点四边形.若一个四边形的中点四边形是一个矩形,则四边形可以是 .
12.如图,将正方形纸片折叠,为折痕,点落在对角线上的点处,则的度数为 .
13.在平行四边形中,,,若,则平行四边形的面积为 .
14.如图为某城市部分街道示意图,四边形ABCD为正方形,点G在对角线BD上,GE⊥CD,GF⊥BC,AD=1 500 m,小敏行走的路线为B→A→G→E,小聪行走的路线为B→A→D→E→F.若小敏行走的路程为3 100 m,则AG+GE= m,由此可得小聪行走的路程为 m.
15.如图所示,RtABC中,O为斜边中点,CD为斜边上的高.若OC=3,DC=,则ABC的面积是 .
16.如图,在正方形中,以为边在正方形内作等边,连接,则的度数为 .
17.如图,在矩形中,对角线,相交于点,,则的度数是 .
18.如图,在平面直角坐标系中有一个边长为1的正方形,边,分别在轴、轴上,如果以对角线为边作第二个正方形,再以对角线为边作第三个正方形,……,照此规律作下去,则点的坐标为 ;点的坐标为 .
19.如图,矩形的对角线相交于点,过点作交于点,若,的面积为6,则 .
20.如图,对折矩形纸片ABCD,使AB与DC重合得到折痕EF,将纸片展平,再一次折叠,使点D落到EF上点G处,并使折痕经过点A,已知BC=2,则线段EG的长度为 .
三、解答题
21.如图,在菱形中,,,点E是边的中点,点M是边上的一个动点(不与点A重合),延长交的延长线于点N,连接,.
(1)求证:四边形是平行四边形.
(2)①当______时,四边形是矩形;
②当______时,四边形是菱形.
22.图1是“口子窖”酒的一个由铁皮制成的包装底盒,它是一个无盖的六棱柱形状的盒子(如图2),侧面是矩形或正方形.经测量,底面六边形有三条边的长是9,有三条边的长是3,每个内角都是,该六棱校的高为3.现沿它的侧棱剪开展平,得到如图3的平面展开图.
(1)制作这种底盒时,可以按图4中虚线裁剪出如图3的模片.现有一块长为17.5、宽为16.5的长方形铁皮,请问能否按图4的裁剪方法制作这样的无盖底盒?并请你说明理由;
(2)如果用一块正三角形铁皮按图5中虚线裁剪出如图3的模片,那么这个正三角形的边长至少应为 .(说明:以上裁剪均不计接缝处损耗.)
23.(1)如图1,在四边形中,,为上一点,连接,.
①若平分,平分,求的度数;
②若,,为中点,求证:为等腰直角三角形;
(2)某工程队需要在,两棵树的前方建立一座八角亭.按如下方法选址:如图2,甲工人从点直走到树处,然后向右转后再直走一段路等于的长度到点处;乙工人从点直走到树处,然后向左转后再直走一段路等于的长度到点处.工程队队长打算把八角亭建在的中点处.过几天,工程队带着建筑材料来施工,却发现忘记标记起始点,正当大家懊恼时,队长说:别急,只要找到,两棵树连线的中点,由点引的垂线,再往,两棵树前方量出的长度的一半,就能找到之前的点(如图3所示).你觉得队长的方法对吗?为什么?
24.进入世纪后,我国科技技术高速发展,很多行业领先于全球其他国家,物流快递行业就是其中之一,随着快递数量的暴增,某大型物流企业为提高效率,启用机器人分拣快递,在仓储中心有机器人的环形轨道,环形轨道是一个直角梯形(图①),且轨道和轨道在东西方向上,如图所示,,,,,,若机器人从点出发,搬运大件快递到点,运动速度是,机器人从点出发,搬运小件快递到点,然后返回点,运动速度是,假设两个机器人同时出发,机器人的运动时间是秒.
(1)在机器人从点到点的运动过程中,若用字母t表示下列线段长,则________,________;
(2)在机器人从点到点的运动过程中,当四边形是平行四边形时,求时间;
(3)从运动开始到机器人回到点的过程中,是否会出现机器P刚好在机器人的正北方向的时候,若存在,请算出机器人的运动时间,若不存在,请说明理由.
25.小兰的课桌桌面的形状如图所示,她想检查一下它是不是矩形,如果手头仅有一根比较长的绳子,请你帮她想一下应该如何做,并说明原因.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
2.D
3.D
4.C
5.D
6.A
7.C
8.C
9.A
10.A
11.正方形(答案不唯一,对角线互相垂直的四边形均可)
12.
13.
14. 1600 4600
15.
16.
17./55度
18.
19.
20.
21.(1)略 (2)①1;②2
22.(1)能,略 (2)
23.(1)①②略;(2)队长说法正确,略
24.(1),
(2)
(3)存在,机器刚好在机器人的正北方向的时候,的值为或
25.略
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
