新北师大版九年级下第三章《圆》单元检测卷A
文档属性
| 名称 | 新北师大版九年级下第三章《圆》单元检测卷A |  | |
| 格式 | zip | ||
| 文件大小 | 167.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2015-12-15 10:44:42 | ||
图片预览


文档简介
新北师大版九年级下第三章《圆》单元检测卷A
(全卷满分100分 限时90分钟)
一、选择题(每题3分,共36分)
1.P为⊙O内与O不重合的一点,则下列说法正确的是( )
A.点P到⊙O上任一点的距离都小于⊙O的半径
B.⊙O上有两点到点P的距离等于⊙O的半径
C.⊙O上有两点到点P的距离最小
D.⊙O上有两点到点P的距离最大
2.若⊙A的半径为5,点A的坐标为(3,4),点P的坐标为(5,8),则点P的位置为( )A.在⊙A内 B.在⊙A上 C.在⊙A外 D.不确定
3.半径为R的圆中,垂直平分半径的弦长等于( )
A.R B.R C.R D.2R
4.已知:如图,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O的半径为( )A.4cm B.5cm C.4cm D.2cm
5.下列说法正确的是( )
A.顶点在圆上的角是圆周角 B.两边都和圆相交的角是圆周角
C.圆心角是圆周角的2倍 D.圆周角度数等于它所对圆心角度数的一半
6.下列说法错误的是( )
A.等弧所对圆周角相等 B.同弧所对圆周角相等
C.同圆中,相等的圆周角所对弧也相等. D.同圆中,等弦所对的圆周角相等
7.⊙O内最长弦长为m,直线ι与⊙O相离,设点O到ι的距离为d,则d与m的关系是( )A.d=m B.d>m C.d> D.d<
8.菱形对角线的交点为O,以O为圆心,以O到菱形一边的距离为半径的圆与其他几边的关系为( )A.相交 B.相切 C.相离 D.不能确定
9.如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )21·世纪*教育网
A.20° B.40° C.80° D.100°
10. 如图,AB是⊙O的直径,P是AB延长线上的一点,PC切⊙O于点C,PC=3,PB=1,则⊙O的半径等于( )21教育网
A B 3 C 4 D
11.正方形ABCD的边长是2cm,以直线AB为轴旋转一周,所得到的圆柱的侧面积为( ).
A 16π B 8π C 4π D 4
12.如图,A,B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
A、70° B、35° C、20° D、10°
二、填空题(每题3分,共12分)
13.平面上一点和⊙O上的最近点距离为5cm,最远距离为9cm,则这个圆的半径是 __________cm.【出处:21教育名师】
14.⊙O的半径为6,⊙O的一条弦AB为6,以3为半径的同心圆与直线AB的位置关系是 .【版权所有:21教育】
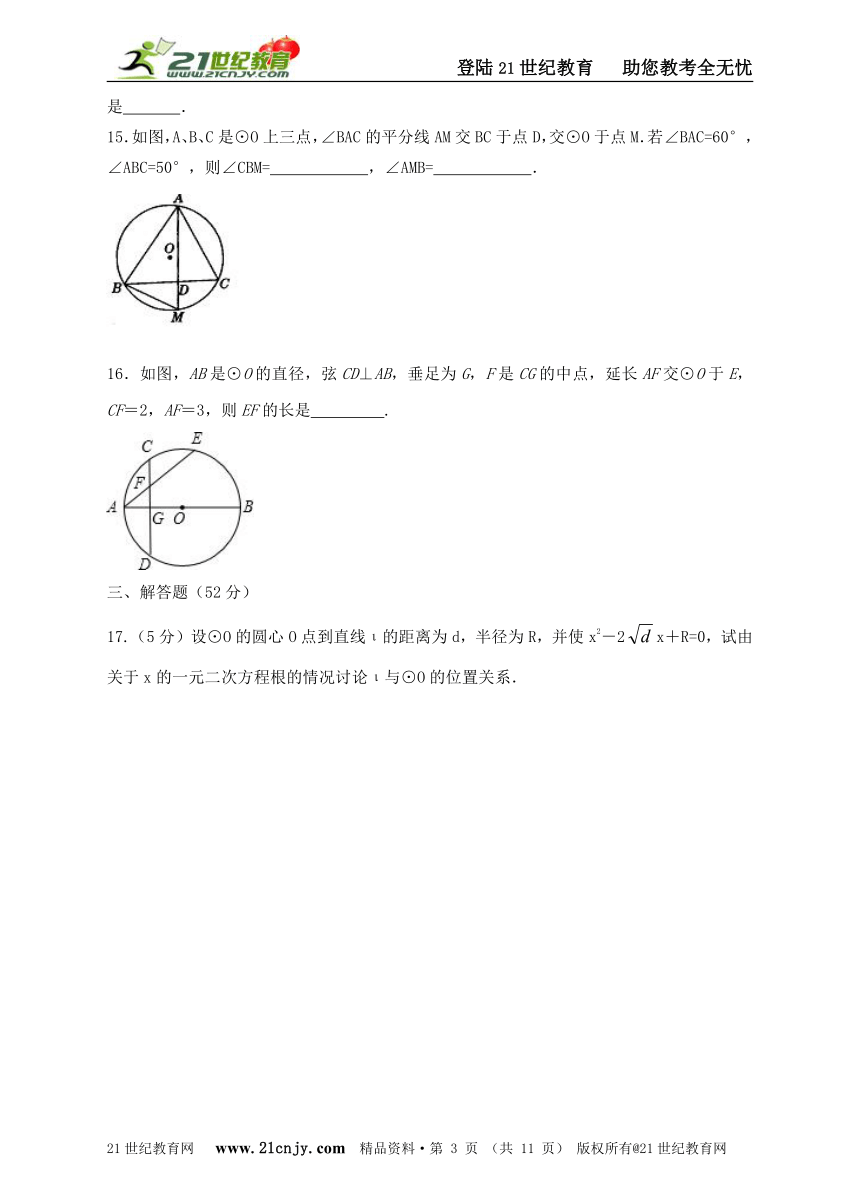
15.如图,A、B、C是⊙O上三点,∠BAC的平分线AM交BC于点D,交⊙O于点M.若∠BAC=60°,
∠ABC=50°,则∠CBM= ,∠AMB= .
16.如图,AB是⊙O的直径,弦CD⊥AB,垂足为G,F是CG的中点,延长AF交⊙O于E,CF=2,AF=3,则EF的长是 .21教育名师原创作品
三、解答题(52分)
17.(5分)设⊙O的圆心O点到直线ι的距离为d,半径为R,并使x2-2x+R=0,试由关于x的一元二次方程根的情况讨论ι与⊙O的位置关系.【来源:21·世纪·教育·网】
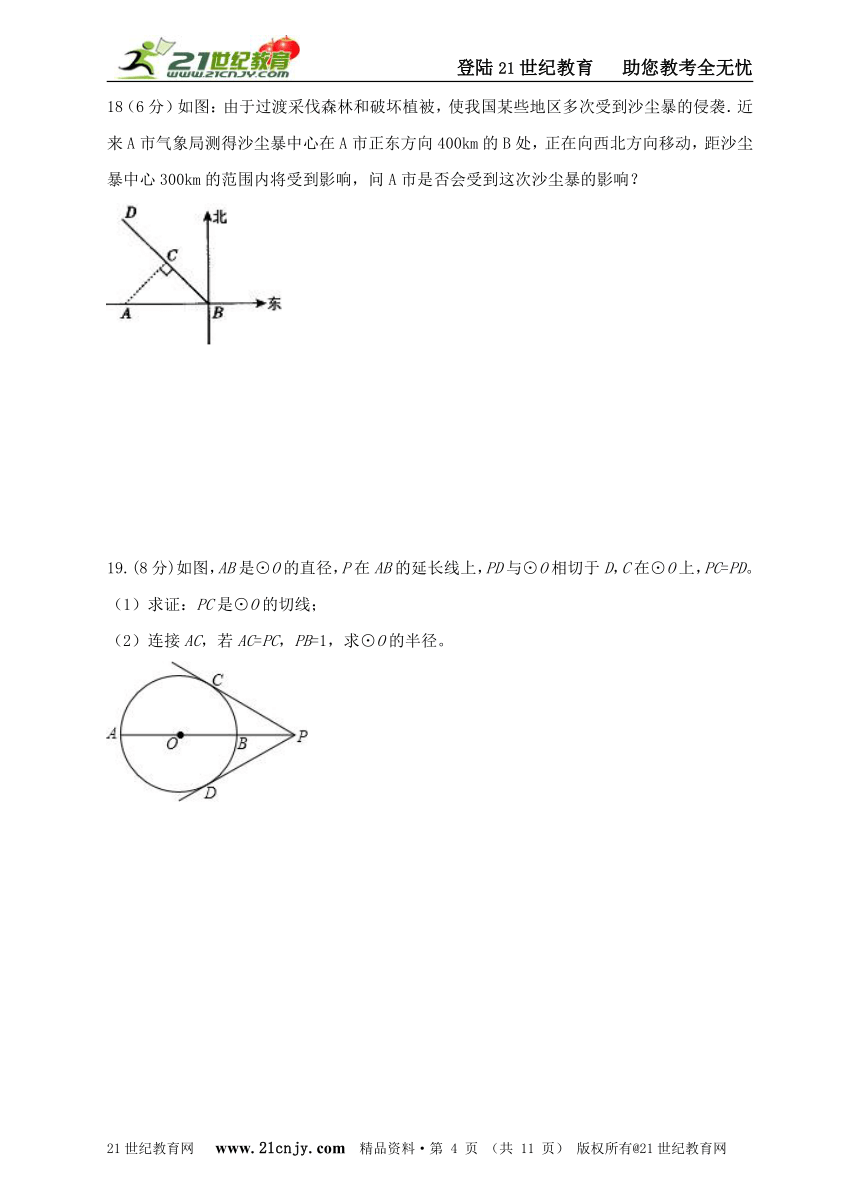
18(6分)如图:由于过渡采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭.近来A市气象局测得沙尘暴中心在A市正东方向400km的B处,正在向西北方向移动,距沙尘暴中心300km的范围内将受到影响,问A市是否会受到这次沙尘暴的影响?
19.(8分)如图,AB是⊙O的直径,P在AB的延长线上,PD与⊙O相切于D,C在⊙O上,PC=PD。
(1)求证:PC是⊙O的切线;
(2)连接AC,若AC=PC,PB=1,求⊙O的半径。
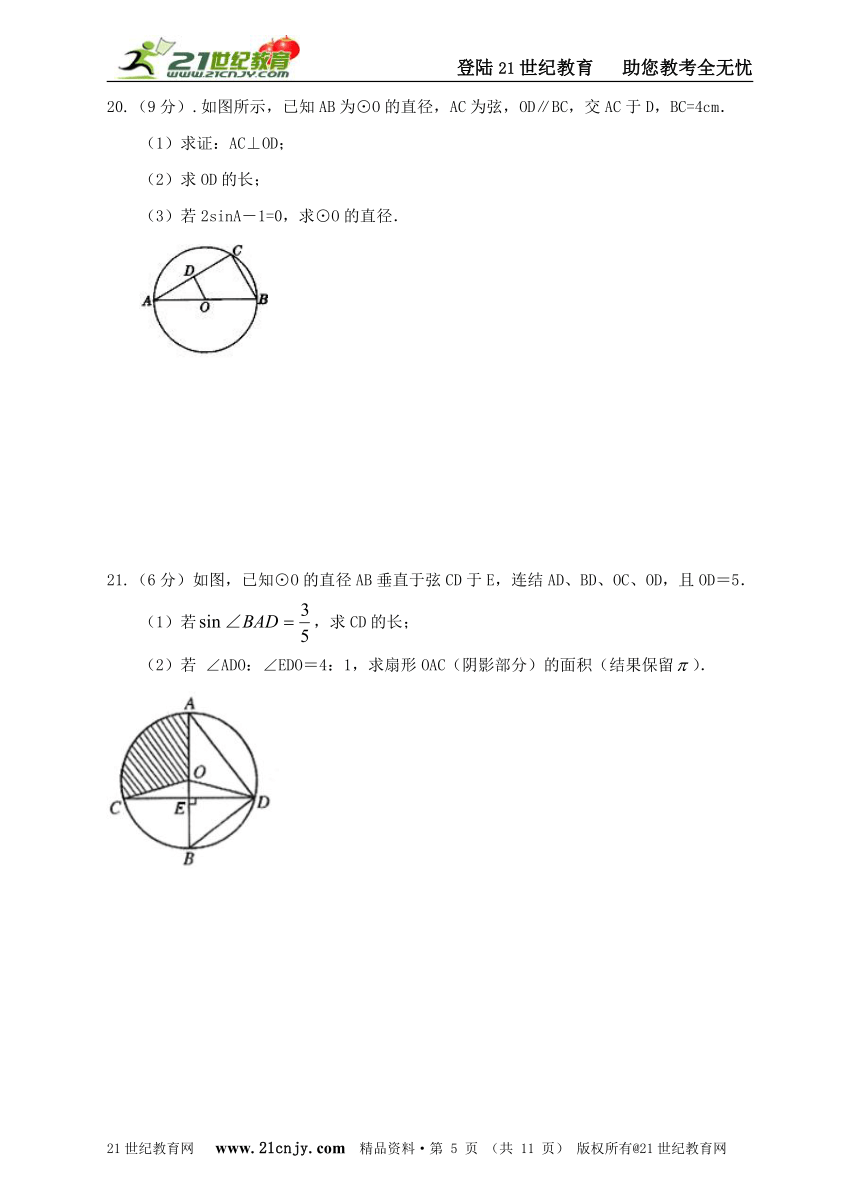
20.(9分).如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=4cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若2sinA-1=0,求⊙O的直径.
21.(6分)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5.
(1)若,求CD的长;
(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留).
22.(9分)如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.21世纪教育网版权所有
(1)求证:∠ADB=∠E;(3分)
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由.(3分)
(3)当AB=5,BC=6时,求⊙O的半径.(3分)
23.(9分)如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交轴于D点,过点D作DF⊥AE于点F.
(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.21·cn·jy·com
参考答案:
一.选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
C
B
D
D
C
B
C
C
B
C
二.填空题:
题 号
13
14
15
16
答 案
2
相切
30?,70?
4
三.解答题:
17.解:△=(-2)2-4R=4d-4R,∴当△>0,即4d-4R>0,得d>R时,ι与⊙O相离;21cnjy.com
当△=0,即4d-4R=0,得d=R时,ι与⊙O相切;
当△>0,即4d-4R<0,得d<R时,ι与⊙O相交.
18.解:过A作AC⊥BD于C.
由题意,得AB=400km,∠DBA=45°.在Rt△ACB中,
∵sin∠ABC=,∴AC=AB·sin∠ABC=400×=200≈282.8(km).
∵200<300,∴A市将受到沙尘暴的影响.
(1)连接OC、OD,在?PCO和?PDO中, , 所以?PCO≌?PDO, 又因为PD是圆的切线,所以∠OCP=∠ODP=90°,即PC是⊙O的切线. www.21-cn-jy.com
(2)因为AC=PC, 所以∠CAO=∠CPO又因为∠COP=2∠CAO∴∠COP=2∠CPO, 又因为∠OCP=90?,所以∠CPA=30°,所以OP=2OC,PB=1,∴2r=r+1,∴r=1.
20.解:(1)∵AB是⊙O的直径,∴∠C=90°.
∵OD∥BC,∴∠ADO=∠C=90°.∴AC⊥OD.
(2)∵OD∥BC,又∵O是AB的中点,∴OD是△ABC的中位线.
∴OD=BC=×4=2(cm).
(3)∵2sinA-1=0,∴sinA=.∴∠A=30°.在Rt△ABC中,∠A=30°,∴BC=AB.∴AB=2BC=8(cm).即⊙O的直径是8cm.2·1·c·n·j·y
21.解:(1)∵AB是⊙O的直径, OD=5,∴∠ADB=90°,AB=10,在Rt△ABD中,sin∠BAD=,sin∠BAD=,www-2-1-cnjy-com
∴,∴BD=6,∴AD=
∵∠ADB=90°,AB⊥CD,∴DE×AB=AD×BD,CE=DE,
∴DE=4.8,CD=2DE=9.6.
(2)∵AB是⊙O的直径, AB⊥CD,∴ =,=,∴∠BAD=∠CDB,∠AOC=∠AOD,
∵AO=DO,∴∠BAD=∠ADO,∴∠CDB=∠ADO
设∠ADO=4x,则∠CDB=4x. 由∠ADO:∠EDO=4:1,则∠EDO=x.
∵∠ADO+∠EDB+∠EDO=90°,∴4x+4x+x=90°,解得:x=10°,∴∠AOD=180°(∠OAD+∠ADO)=100°,∴∠AOC=∠AOD=100°,∴
22.解:(1)在?ABC中,∵AB=AC, ∴∠ABC=∠C。 ∵DE∥BC,∴∠ABC=∠E, ∴∠E=∠C。 又∵∠ADB=∠C, ∴∠ADB=∠E。 (2)当点D是弧BC的中点时,DE是⊙O的切线。 ∵当点D是弧BC的中点时,AD⊥BC,且AD过圆心O 又∵DE∥BC,∴ AD⊥ED。 ∴ DE是⊙O的切线。2-1-c-n-j-y
(3)连结BO、AO,并延长AO交BC于点F, 则AF⊥BC,且BF=BC=3。 又∵AB=5,∴AF=4。 设⊙O的半径为r, 在Rt△OBF中,OF=4-r,OB=r,BF=3, ∴ r2=32+(4-r)2 解得:r=,? ∴⊙O的半径是【来源:21cnj*y.co*m】
23.(1)解:在矩形OABC中,设OC=x,则OA=x+2
∴x(x+2)=15∴x1=3,x2=﹣5∴x2=﹣5(不合题意,舍去)
∴OC=3,OA=5;
(2)证明:连接O′D;
∵在矩形OABC中,OC=AB,∠OCB=∠ABC=90°,CE=BE=,
∴△0CE≌△ABE,∴EA=EO,∴∠1=∠2;
∵在⊙O′中,O′O=O′D,∴∠1=∠3,
∴∠3=∠2,∴O′D∥AE;∴EA=EO,∴∠1=∠2;
∵在⊙O′中,O′O=O′D,∴∠1=∠3,∴∠3=∠2,∴O′D∥AE;
∵DF⊥AE,∴DF⊥O′D,
∵点D在⊙O′上,O′D为⊙O′的半径,∴DF为⊙O′切线;
(3)解:不同意.
理由如下:
①当A0=AP时,以点A为圆心,以AO为半径画弧交BC于P1和P4两点
过P1点作P1H⊥OA于点H,P1H=0C=3;
∵APl=OA=5,∴AH=4,∴OH=l,
求得点P1(1,3)同理可得:P4(9,3);
②当OA=OP时,同上可求得P2(4,3),P3(﹣4,3),
∴在直线BC上,除了E点外,既存在⊙O′内的点P1,又存在⊙O′外的点P2、P3、P4,它们分别使△AOP为等腰三角形. 21*cnjy*com
(全卷满分100分 限时90分钟)
一、选择题(每题3分,共36分)
1.P为⊙O内与O不重合的一点,则下列说法正确的是( )
A.点P到⊙O上任一点的距离都小于⊙O的半径
B.⊙O上有两点到点P的距离等于⊙O的半径
C.⊙O上有两点到点P的距离最小
D.⊙O上有两点到点P的距离最大
2.若⊙A的半径为5,点A的坐标为(3,4),点P的坐标为(5,8),则点P的位置为( )A.在⊙A内 B.在⊙A上 C.在⊙A外 D.不确定
3.半径为R的圆中,垂直平分半径的弦长等于( )
A.R B.R C.R D.2R
4.已知:如图,⊙O的直径CD垂直于弦AB,垂足为P,且AP=4cm,PD=2cm,则⊙O的半径为( )A.4cm B.5cm C.4cm D.2cm
5.下列说法正确的是( )
A.顶点在圆上的角是圆周角 B.两边都和圆相交的角是圆周角
C.圆心角是圆周角的2倍 D.圆周角度数等于它所对圆心角度数的一半
6.下列说法错误的是( )
A.等弧所对圆周角相等 B.同弧所对圆周角相等
C.同圆中,相等的圆周角所对弧也相等. D.同圆中,等弦所对的圆周角相等
7.⊙O内最长弦长为m,直线ι与⊙O相离,设点O到ι的距离为d,则d与m的关系是( )A.d=m B.d>m C.d> D.d<
8.菱形对角线的交点为O,以O为圆心,以O到菱形一边的距离为半径的圆与其他几边的关系为( )A.相交 B.相切 C.相离 D.不能确定
9.如图所示,四边形ABCD为⊙O的内接四边形,E为AB延长线的上一点,∠CBE=40°,则∠AOC等于( )21·世纪*教育网
A.20° B.40° C.80° D.100°
10. 如图,AB是⊙O的直径,P是AB延长线上的一点,PC切⊙O于点C,PC=3,PB=1,则⊙O的半径等于( )21教育网
A B 3 C 4 D
11.正方形ABCD的边长是2cm,以直线AB为轴旋转一周,所得到的圆柱的侧面积为( ).
A 16π B 8π C 4π D 4
12.如图,A,B是⊙O上的两点,AC是⊙O的切线,∠B=70°,则∠BAC等于( )
A、70° B、35° C、20° D、10°
二、填空题(每题3分,共12分)
13.平面上一点和⊙O上的最近点距离为5cm,最远距离为9cm,则这个圆的半径是 __________cm.【出处:21教育名师】
14.⊙O的半径为6,⊙O的一条弦AB为6,以3为半径的同心圆与直线AB的位置关系是 .【版权所有:21教育】
15.如图,A、B、C是⊙O上三点,∠BAC的平分线AM交BC于点D,交⊙O于点M.若∠BAC=60°,
∠ABC=50°,则∠CBM= ,∠AMB= .
16.如图,AB是⊙O的直径,弦CD⊥AB,垂足为G,F是CG的中点,延长AF交⊙O于E,CF=2,AF=3,则EF的长是 .21教育名师原创作品
三、解答题(52分)
17.(5分)设⊙O的圆心O点到直线ι的距离为d,半径为R,并使x2-2x+R=0,试由关于x的一元二次方程根的情况讨论ι与⊙O的位置关系.【来源:21·世纪·教育·网】
18(6分)如图:由于过渡采伐森林和破坏植被,使我国某些地区多次受到沙尘暴的侵袭.近来A市气象局测得沙尘暴中心在A市正东方向400km的B处,正在向西北方向移动,距沙尘暴中心300km的范围内将受到影响,问A市是否会受到这次沙尘暴的影响?
19.(8分)如图,AB是⊙O的直径,P在AB的延长线上,PD与⊙O相切于D,C在⊙O上,PC=PD。
(1)求证:PC是⊙O的切线;
(2)连接AC,若AC=PC,PB=1,求⊙O的半径。
20.(9分).如图所示,已知AB为⊙O的直径,AC为弦,OD∥BC,交AC于D,BC=4cm.
(1)求证:AC⊥OD;
(2)求OD的长;
(3)若2sinA-1=0,求⊙O的直径.
21.(6分)如图,已知⊙O的直径AB垂直于弦CD于E,连结AD、BD、OC、OD,且OD=5.
(1)若,求CD的长;
(2)若 ∠ADO:∠EDO=4:1,求扇形OAC(阴影部分)的面积(结果保留).
22.(9分)如图,⊙O是△ABC的外接圆,且AB=AC,点D在弧BC上运动,过点D作DE∥BC,DE交AB的延长线于点E,连结AD、BD.21世纪教育网版权所有
(1)求证:∠ADB=∠E;(3分)
(2)当点D运动到什么位置时,DE是⊙O的切线?请说明理由.(3分)
(3)当AB=5,BC=6时,求⊙O的半径.(3分)
23.(9分)如图,在平面直角坐标系中,矩形ABCO的面积为15,边OA比OC大2.E为BC的中点,以OE为直径的⊙O′交轴于D点,过点D作DF⊥AE于点F.
(1)求OA、OC的长;
(2)求证:DF为⊙O′的切线;
(3)小明在解答本题时,发现△AOE是等腰三角形.由此,他断定:“直线BC上一定存在除点E以外的点P,使△AOP也是等腰三角形,且点P一定在⊙O′外”.你同意他的看法吗?请充分说明理由.21·cn·jy·com
参考答案:
一.选择题:
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
C
B
D
D
C
B
C
C
B
C
二.填空题:
题 号
13
14
15
16
答 案
2
相切
30?,70?
4
三.解答题:
17.解:△=(-2)2-4R=4d-4R,∴当△>0,即4d-4R>0,得d>R时,ι与⊙O相离;21cnjy.com
当△=0,即4d-4R=0,得d=R时,ι与⊙O相切;
当△>0,即4d-4R<0,得d<R时,ι与⊙O相交.
18.解:过A作AC⊥BD于C.
由题意,得AB=400km,∠DBA=45°.在Rt△ACB中,
∵sin∠ABC=,∴AC=AB·sin∠ABC=400×=200≈282.8(km).
∵200<300,∴A市将受到沙尘暴的影响.
(1)连接OC、OD,在?PCO和?PDO中, , 所以?PCO≌?PDO, 又因为PD是圆的切线,所以∠OCP=∠ODP=90°,即PC是⊙O的切线. www.21-cn-jy.com
(2)因为AC=PC, 所以∠CAO=∠CPO又因为∠COP=2∠CAO∴∠COP=2∠CPO, 又因为∠OCP=90?,所以∠CPA=30°,所以OP=2OC,PB=1,∴2r=r+1,∴r=1.
20.解:(1)∵AB是⊙O的直径,∴∠C=90°.
∵OD∥BC,∴∠ADO=∠C=90°.∴AC⊥OD.
(2)∵OD∥BC,又∵O是AB的中点,∴OD是△ABC的中位线.
∴OD=BC=×4=2(cm).
(3)∵2sinA-1=0,∴sinA=.∴∠A=30°.在Rt△ABC中,∠A=30°,∴BC=AB.∴AB=2BC=8(cm).即⊙O的直径是8cm.2·1·c·n·j·y
21.解:(1)∵AB是⊙O的直径, OD=5,∴∠ADB=90°,AB=10,在Rt△ABD中,sin∠BAD=,sin∠BAD=,www-2-1-cnjy-com
∴,∴BD=6,∴AD=
∵∠ADB=90°,AB⊥CD,∴DE×AB=AD×BD,CE=DE,
∴DE=4.8,CD=2DE=9.6.
(2)∵AB是⊙O的直径, AB⊥CD,∴ =,=,∴∠BAD=∠CDB,∠AOC=∠AOD,
∵AO=DO,∴∠BAD=∠ADO,∴∠CDB=∠ADO
设∠ADO=4x,则∠CDB=4x. 由∠ADO:∠EDO=4:1,则∠EDO=x.
∵∠ADO+∠EDB+∠EDO=90°,∴4x+4x+x=90°,解得:x=10°,∴∠AOD=180°(∠OAD+∠ADO)=100°,∴∠AOC=∠AOD=100°,∴
22.解:(1)在?ABC中,∵AB=AC, ∴∠ABC=∠C。 ∵DE∥BC,∴∠ABC=∠E, ∴∠E=∠C。 又∵∠ADB=∠C, ∴∠ADB=∠E。 (2)当点D是弧BC的中点时,DE是⊙O的切线。 ∵当点D是弧BC的中点时,AD⊥BC,且AD过圆心O 又∵DE∥BC,∴ AD⊥ED。 ∴ DE是⊙O的切线。2-1-c-n-j-y
(3)连结BO、AO,并延长AO交BC于点F, 则AF⊥BC,且BF=BC=3。 又∵AB=5,∴AF=4。 设⊙O的半径为r, 在Rt△OBF中,OF=4-r,OB=r,BF=3, ∴ r2=32+(4-r)2 解得:r=,? ∴⊙O的半径是【来源:21cnj*y.co*m】
23.(1)解:在矩形OABC中,设OC=x,则OA=x+2
∴x(x+2)=15∴x1=3,x2=﹣5∴x2=﹣5(不合题意,舍去)
∴OC=3,OA=5;
(2)证明:连接O′D;
∵在矩形OABC中,OC=AB,∠OCB=∠ABC=90°,CE=BE=,
∴△0CE≌△ABE,∴EA=EO,∴∠1=∠2;
∵在⊙O′中,O′O=O′D,∴∠1=∠3,
∴∠3=∠2,∴O′D∥AE;∴EA=EO,∴∠1=∠2;
∵在⊙O′中,O′O=O′D,∴∠1=∠3,∴∠3=∠2,∴O′D∥AE;
∵DF⊥AE,∴DF⊥O′D,
∵点D在⊙O′上,O′D为⊙O′的半径,∴DF为⊙O′切线;
(3)解:不同意.
理由如下:
①当A0=AP时,以点A为圆心,以AO为半径画弧交BC于P1和P4两点
过P1点作P1H⊥OA于点H,P1H=0C=3;
∵APl=OA=5,∴AH=4,∴OH=l,
求得点P1(1,3)同理可得:P4(9,3);
②当OA=OP时,同上可求得P2(4,3),P3(﹣4,3),
∴在直线BC上,除了E点外,既存在⊙O′内的点P1,又存在⊙O′外的点P2、P3、P4,它们分别使△AOP为等腰三角形. 21*cnjy*com
