函数问题解题技巧课件
图片预览




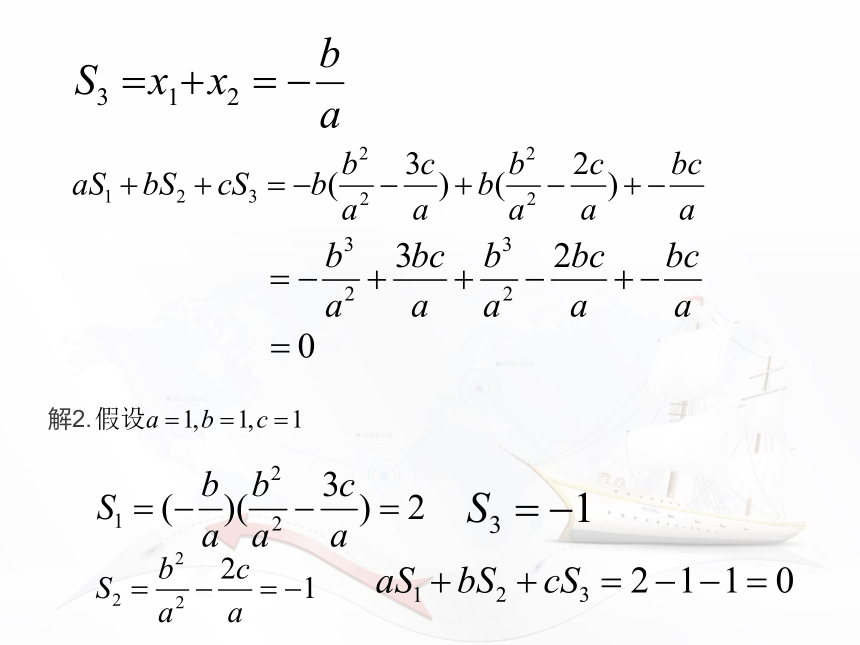

文档简介
课件13张PPT。数学解题方法例1.
【分析】我们发现该题的函数是一个抽象函数,没有具体的解析式。那么我们不妨根据题设假设出一个函数y满足题设。例2.已知a,b,c为实数,并且对于任意实数x恒有 |x+a|+|2x+b|=|3x+c| ,则a:b:c_____。一 特殊值法
数学中通过把未知量假设成为一个具体的数,进行计算或解答的方法。这个特殊值必须满足三个条件:首先,无论这个量的值是多少,对最终结果所要求的量的值没有影响;其次,这个量应该要跟最终结果所要求的量有相对紧密的联系;最后,这个量在整个题干中给出的等量关系是一个不可或缺的量。
注意:特殊值法对于假设量的选择有一定的技巧性,需要大家多做练习,并且假设的特殊值必须满足题设从一般到特殊,从抽象到具体练习题.
1.
—————
解1.根据韦达定理
解2. 1. _________
解、
2. ______
二、换元法
解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理。
换元的方法有:局部换元、三角换元、均值换元等。局部换元又称整体换元,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现。从未知到已知 从复杂到简单例3
【分析】将对数方程进行等价变形,转化为一元二次方程在某个范围内有实解的问题,再利用二次函数的图像进行解决。【解】 原方程变形为
即:
设曲线y=(x-2) , x∈(0,3)和直线y=1-m,图像如图所示。由图可知:
① 当1-m=0时,有唯一解,m=1;
②当1≤1-m<4时,有唯一解,即-3∴ m=1或-3此题也可设曲线y=-(x-2)+1 , x∈(0,3)和直线y=m后画出图像求解。例4、若方程lg(-x^2+3x-m)=lg(3-x)在x∈(0,3)内有唯一解,求实数m的取值范围 数形结合是一个数学思想方法,包含“以形助数”和“以数辅形”两个方面,其应用大致可以分为两种情形:或者是借助形的生动和直观性来阐明数之间的联系,即以形作为手段,数为目的,比如应用函数的图像来直观地说明函数的性质;或者是借助于数的精确性和规范严密性来阐明形的某些属性,即以数作为手段,形作为目的,如应用曲线的方程来精确地阐明曲线的几何性质。三、数形结合代数问题转化为几何问题1.2.3.CBC1.某数加上6,乘以6,减去6,除以6,其结果等于6,则这个数是_____
四、倒推法
当你做一道选择题时,如果没有思路,可以尝试观察一下答案 ,从答案出发寻找思路,把这种方法叫做倒推法。就是从结论到条件。
【分析】我们发现该题的函数是一个抽象函数,没有具体的解析式。那么我们不妨根据题设假设出一个函数y满足题设。例2.已知a,b,c为实数,并且对于任意实数x恒有 |x+a|+|2x+b|=|3x+c| ,则a:b:c_____。一 特殊值法
数学中通过把未知量假设成为一个具体的数,进行计算或解答的方法。这个特殊值必须满足三个条件:首先,无论这个量的值是多少,对最终结果所要求的量的值没有影响;其次,这个量应该要跟最终结果所要求的量有相对紧密的联系;最后,这个量在整个题干中给出的等量关系是一个不可或缺的量。
注意:特殊值法对于假设量的选择有一定的技巧性,需要大家多做练习,并且假设的特殊值必须满足题设从一般到特殊,从抽象到具体练习题.
1.
—————
解1.根据韦达定理
解2. 1. _________
解、
2. ______
二、换元法
解数学题时,把某个式子看成一个整体,用一个变量去代替它,从而使问题得到简化,这叫换元法。换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理。
换元的方法有:局部换元、三角换元、均值换元等。局部换元又称整体换元,是在已知或者未知中,某个代数式几次出现,而用一个字母来代替它从而简化问题,当然有时候要通过变形才能发现。从未知到已知 从复杂到简单例3
【分析】将对数方程进行等价变形,转化为一元二次方程在某个范围内有实解的问题,再利用二次函数的图像进行解决。【解】 原方程变形为
即:
设曲线y=(x-2) , x∈(0,3)和直线y=1-m,图像如图所示。由图可知:
① 当1-m=0时,有唯一解,m=1;
②当1≤1-m<4时,有唯一解,即-3
四、倒推法
当你做一道选择题时,如果没有思路,可以尝试观察一下答案 ,从答案出发寻找思路,把这种方法叫做倒推法。就是从结论到条件。
