数学人教A版(2019)必修二10.1.2事件的关系和运算 课件(共34张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修二10.1.2事件的关系和运算 课件(共34张ppt) |

|
|
| 格式 | pptx | ||
| 文件大小 | 5.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 00:00:00 | ||
图片预览











文档简介
(共34张PPT)
人教A版高一数学必修二第二学期10.1.2事件的关系和运算
10.1 随机事件与概率
10.1.2 事件的关系和运算
1.数学抽象:理解随机试验的概念及特点
2.直观想象:通过动手试验,体会随机事件发生的随机性和规律性; 理解样本点和样本空间,会求所给试验的样本点和样本空间
3.逻辑推理: 理解随机事件、必然事件、不可能事件的概念,并会判断某一事件的性质
4.数学运算:理解事件5种关系并会判断
核心素养目标
教学目标
教学重点:理解随机事件、必然事件、不可能事件的概念,并会判断某一事件的性质
教学难点:理解事件5种关系并会判断
情境导入
一、随机事件间的关系及运算
回忆一下上节讲的一些符号:
样本点ω= 基本事件
样本空间Ω={全体样本点}
=必然事件
随机事件是由具有某些特征的基本事件所组成,
所以
随机事件 = 样本空间Ω的一个子集.
知识讲解
如:E2:袋中摸球.设袋中有10个外形相同的球,分别标有数字1,2,…10.从中任意摸一球,观察球上所标的数字.记 i="摸到标号为i的球"(i=1,2,...,10)
则样本点为:ω={i}
样本空间:Ω={1,2,…,10}
事件D={球的标号是奇数}={1,3,5,7,9}
F={球的标号≤5}={1,2,3,4,5}
D Ω,F Ω D,F均是Ω的子集.
知识讲解
运算 符号 概率论 集合论 venn图
和 AUB 事件A与B有一个发生 A与B的并集
差 A-B 事件A发生而B不发生 A与B的差集
积 AB或A∩B 事件A与B同时发生 A与B的交集
1.运算有三种
知识讲解
事件A与B的并(和事件)
"二事件A,B至少发生一个"也是一个事件,称为事件 A与事件B的和事件.记作AUB,显然AUB={el A或eEB}.
实例 某种产品的合格与否是由该产品的长度与直径是否合格所决定,因此"产品不合格"是"长度不合格"与"直径不合格"的并.
图示事件A与B的并.
知识讲解
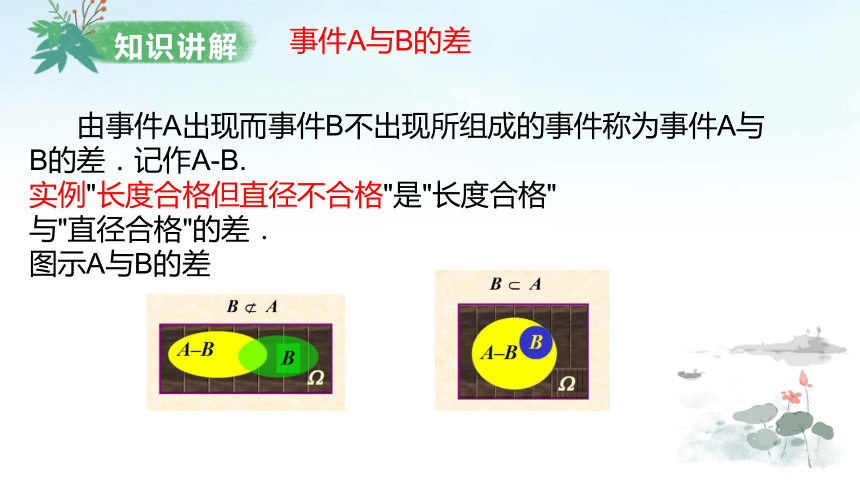
由事件A出现而事件B不出现所组成的事件称为事件A与B的差.记作A-B.
实例"长度合格但直径不合格"是"长度合格"
与"直径合格"的差.
图示A与B的差
事件A与B的差
知识讲解
"二事件A,B同时发生"也是一个事件,称为事件A与事件B的积事件,记作A∩B,显然A∩B={ele A且e B}.
积事件也可记作 A.B或AB.
实例 某种产品的合格与否是由该产品的长度与直径是否合格所决定,因此"产品合格"是"长度合格"与"直径合格"的交或积事件.图示事件A与B的积事件.
事件A与B的交(积事件)
知识讲解
②A1UA2U…UAn=UAi :
i=1
A1,A2,…,An"中至少有一个发生.
A1UA2U...UAn...=UAi :
i=1
A1,A2,…,An",…中至少有一个发生.
②A1∩A2∩…∩An=∩Ai:
i=1
A1,A2,…,An"同时发生。
A1∩A2∩…∩An…=∩Ai:
i=1
A1,A2,…,An,…同时发生.
n
∞
n
n
∞
知识讲解
关系 符号 概率论 集合论 Venn图
包含 A B A发生则 B必发生 A是B的子集
等价 A=B A B且 B A A与B相等
互斥(互不相容) AB= 事件A与B不能同时发生 A与B不相交
对立(互逆) A的对立事件 A的余集 ①AU =Ω ②A =
知识讲解
若事件A出现,必然导致B出现,则称事件B包含事件A,记作B A或A B
实例 "长度不合格"必然导致"产品不合格以"产品不合格"包含"长度不合格".
图示B包含A.
包含关系
知识讲解
事件A与B互不相容(互斥)
事件A的出现必然导致事件B不出现,B 出现也必然导致A不出现,则称事件A与B互不相容,即
AB=
实例 抛掷一枚硬币,"出现花面"与"出现字面"是互不相容的两个事件.
知识讲解
实例 抛掷一枚骰子,观察出现的点数.
"骰子出现1点" "骰子出现2点"
图示A与B互斥
说明 当A B= 时,可将AUB记为"直和"形式A+B.
任意事件A与不可能事件 为互斥
互斥
知识讲解
事件 A 的对立(互逆)事件
设A表示"事件A出现",则"事件A不出现"称为事件A的对立事件或逆事件.记作 .
实例 "骰子出现1点" 对立"骰子不出现1点"
图示A与B的对立.
若A与B互逆,则AUB=Ω且AB= .
对立
知识讲解
注.1.互斥与互逆的关系
如:对于E2,A={2},B={5}
∵AB= ∴A与B互斥
但 AUB={2,5}=Ω={1,2,…,10}
∴A与B不互逆
D ={1,3,5,7,9}与G ={2,4,6,8,10}互逆.
2.必然事件Ω与不可能事件 互逆.
互逆 互斥
知识讲解
对立事件与互斥事件的区别
A、B互斥
A、B对立
AB=
AUB=Ω且AB=
互斥
对立
Ω
A
B
B=
Ω
A
知识讲解
运算法则
1.交换律:(1)AUB=BUA
(2) AB = BA
2.结合律:(1)(AUB)UC=AU(BUC)
(2)(AB)C = A(BC)
3.分配律:(1)(AUB)C=ACUBC
(2)(AB)UC=(AUC)(BUC)AU(BC)=(AUB)(AUC)
知识讲解
下面由文氏图简单说明★式的正确性(AB)
注:此处只能进行简单的说明,不能用这种方法证明,具体证明的方法参看教材例1.2。
知识讲解
(1)AUB=A B
意义:"A,B至少有一发生"的对立事件
是"A,B均不发生".
(2)AB=AUB
意义:"A,B均发生"的对立事件是"A,B
至少有一个不发生".
4.对偶律(De Morgan定理)
知识讲解
例1 设A,B为随机事件,证明
(1)
(2)
证 (1)
知识讲解
(2) A+BA=AUBA
=(AUB)(AUA)
=(AUB)Ω=AUB
AB+AB+ AB
=A(B+B)+ AB=AΩ+ BA = A+ BA=AUB
归纳方法
(1)包含关系、相等关系的判定①事件的包含关系与集合的包含关系相似;②两事件相等的实质为相同事件,即同时发生或同时不发生.(2)判断事件是否互斥的两个步骤第一步,确定每个事件包含的结果;第二步,确定是否有一个结果发生会意味着两个事件都发生,若是,则两个事件不互斥,否则就是互斥的.(3)判断事件是否对立的两个步骤第一步,判断是互斥事件;第二步,确定两个事件必然有一个发生,否则只有互斥,但不对立.
练习
判断下列给出的每对事件,是否为互斥事件,是否为对立事件,并说明理由.从40张扑克牌(红桃、黑桃、方块、梅花点数从1~10各10张)中,任取1张.(1)“抽出红桃”与“抽出黑桃”;(2)“抽出红色牌”与“抽出黑色牌”;(3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”.
练习
解:(1)是互斥事件,不是对立事件.理由是从40张扑克牌中任意抽取1张,“抽出红桃”和“抽出黑桃”是不可能同时发生的,所以是互斥事件.同时,不能保证其中必有一个发生,这是由于还可能抽出“方块”或者“梅花”,因此,二者不是对立事件.(2)既是互斥事件,又是对立事件.理由是从40张扑克牌中,任意抽取1张,“抽出红色牌”与“抽出黑色牌”两个事件不可能同时发生,且其中必有一个发生,所以它们既是互斥事件,又是对立事件.
练习
(3)不是互斥事件,也不是对立事件.理由是从40张扑克牌中任意抽取1张,“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”这两个事件可能同时发生,如抽得点数为10,因此,二者不是互斥事件,当然也不可能是对立事件.
知识拓展
例1 设A,B,C为三个事件,试用这三个事
件的运算关系表示下列事件:
(1)A发生,而B,C都不发生.
可表示为:ABC,或 ABUC;
(2)A,B都发生,C不发生;
ABC,或AB-C;
(3)三个事件同时都发生; ABC;
(4)A,B,C中恰有一个事件发生可表示为: ABC+ABC+ABC;
知识拓展
(5)A,B,C中恰有两个发生可表
示为: ABC+ABC+ABC,
或ABUBCUAC-ABC;
(6)三个事件至少有一个发生;
AUBUC.
知识拓展
例3 设A,B为随机事件,证明:
(1) A-B=A-AB,
(2)AUB=A+BA=AB+ AB+ AB.
证 (1)A-AB=AAB (A-B=AB)
=A(AUB)
=AAUAB= UAB =AB=A-B.
知识拓展
(2) A+BA=AUBA
=(AUB)(AUA)
=(AUB)Ω=AUB.
AB+AB+ AB
=A(B+B)+AB=AΩ+BA =A+BA=AUB.
小结
二、小结
1.随机事件间的关系(六种)
2.事件间的运算规律(四种)
3.概率论与集合论之间术语的对应关系
(见下表)
小结
概率论与集合论之间的对应关系
记号 概率论 集合论
样本空间,必然事件 不可能事件 基本事件 随机事件 A的对立事件 A发生必然导致B发生 事件A与事件B相等 空间(全集)
空集
元素
子集
A的补集
A是B的子集
A集合与B集合相等
小结
AUB 事件A与事件B的和 A集合与B集合的并集
AB 事件A与B的积事件 A集合与B集合的交集
A-B 事件A与事件B的差 A与B两集合的差集
AB= 事件A与B互不相容 A与B两集合中没有相同的元素
人教A版高一数学必修二第二学期10.1.2事件的关系和运算
10.1 随机事件与概率
10.1.2 事件的关系和运算
1.数学抽象:理解随机试验的概念及特点
2.直观想象:通过动手试验,体会随机事件发生的随机性和规律性; 理解样本点和样本空间,会求所给试验的样本点和样本空间
3.逻辑推理: 理解随机事件、必然事件、不可能事件的概念,并会判断某一事件的性质
4.数学运算:理解事件5种关系并会判断
核心素养目标
教学目标
教学重点:理解随机事件、必然事件、不可能事件的概念,并会判断某一事件的性质
教学难点:理解事件5种关系并会判断
情境导入
一、随机事件间的关系及运算
回忆一下上节讲的一些符号:
样本点ω= 基本事件
样本空间Ω={全体样本点}
=必然事件
随机事件是由具有某些特征的基本事件所组成,
所以
随机事件 = 样本空间Ω的一个子集.
知识讲解
如:E2:袋中摸球.设袋中有10个外形相同的球,分别标有数字1,2,…10.从中任意摸一球,观察球上所标的数字.记 i="摸到标号为i的球"(i=1,2,...,10)
则样本点为:ω={i}
样本空间:Ω={1,2,…,10}
事件D={球的标号是奇数}={1,3,5,7,9}
F={球的标号≤5}={1,2,3,4,5}
D Ω,F Ω D,F均是Ω的子集.
知识讲解
运算 符号 概率论 集合论 venn图
和 AUB 事件A与B有一个发生 A与B的并集
差 A-B 事件A发生而B不发生 A与B的差集
积 AB或A∩B 事件A与B同时发生 A与B的交集
1.运算有三种
知识讲解
事件A与B的并(和事件)
"二事件A,B至少发生一个"也是一个事件,称为事件 A与事件B的和事件.记作AUB,显然AUB={el A或eEB}.
实例 某种产品的合格与否是由该产品的长度与直径是否合格所决定,因此"产品不合格"是"长度不合格"与"直径不合格"的并.
图示事件A与B的并.
知识讲解
由事件A出现而事件B不出现所组成的事件称为事件A与B的差.记作A-B.
实例"长度合格但直径不合格"是"长度合格"
与"直径合格"的差.
图示A与B的差
事件A与B的差
知识讲解
"二事件A,B同时发生"也是一个事件,称为事件A与事件B的积事件,记作A∩B,显然A∩B={ele A且e B}.
积事件也可记作 A.B或AB.
实例 某种产品的合格与否是由该产品的长度与直径是否合格所决定,因此"产品合格"是"长度合格"与"直径合格"的交或积事件.图示事件A与B的积事件.
事件A与B的交(积事件)
知识讲解
②A1UA2U…UAn=UAi :
i=1
A1,A2,…,An"中至少有一个发生.
A1UA2U...UAn...=UAi :
i=1
A1,A2,…,An",…中至少有一个发生.
②A1∩A2∩…∩An=∩Ai:
i=1
A1,A2,…,An"同时发生。
A1∩A2∩…∩An…=∩Ai:
i=1
A1,A2,…,An,…同时发生.
n
∞
n
n
∞
知识讲解
关系 符号 概率论 集合论 Venn图
包含 A B A发生则 B必发生 A是B的子集
等价 A=B A B且 B A A与B相等
互斥(互不相容) AB= 事件A与B不能同时发生 A与B不相交
对立(互逆) A的对立事件 A的余集 ①AU =Ω ②A =
知识讲解
若事件A出现,必然导致B出现,则称事件B包含事件A,记作B A或A B
实例 "长度不合格"必然导致"产品不合格以"产品不合格"包含"长度不合格".
图示B包含A.
包含关系
知识讲解
事件A与B互不相容(互斥)
事件A的出现必然导致事件B不出现,B 出现也必然导致A不出现,则称事件A与B互不相容,即
AB=
实例 抛掷一枚硬币,"出现花面"与"出现字面"是互不相容的两个事件.
知识讲解
实例 抛掷一枚骰子,观察出现的点数.
"骰子出现1点" "骰子出现2点"
图示A与B互斥
说明 当A B= 时,可将AUB记为"直和"形式A+B.
任意事件A与不可能事件 为互斥
互斥
知识讲解
事件 A 的对立(互逆)事件
设A表示"事件A出现",则"事件A不出现"称为事件A的对立事件或逆事件.记作 .
实例 "骰子出现1点" 对立"骰子不出现1点"
图示A与B的对立.
若A与B互逆,则AUB=Ω且AB= .
对立
知识讲解
注.1.互斥与互逆的关系
如:对于E2,A={2},B={5}
∵AB= ∴A与B互斥
但 AUB={2,5}=Ω={1,2,…,10}
∴A与B不互逆
D ={1,3,5,7,9}与G ={2,4,6,8,10}互逆.
2.必然事件Ω与不可能事件 互逆.
互逆 互斥
知识讲解
对立事件与互斥事件的区别
A、B互斥
A、B对立
AB=
AUB=Ω且AB=
互斥
对立
Ω
A
B
B=
Ω
A
知识讲解
运算法则
1.交换律:(1)AUB=BUA
(2) AB = BA
2.结合律:(1)(AUB)UC=AU(BUC)
(2)(AB)C = A(BC)
3.分配律:(1)(AUB)C=ACUBC
(2)(AB)UC=(AUC)(BUC)AU(BC)=(AUB)(AUC)
知识讲解
下面由文氏图简单说明★式的正确性(AB)
注:此处只能进行简单的说明,不能用这种方法证明,具体证明的方法参看教材例1.2。
知识讲解
(1)AUB=A B
意义:"A,B至少有一发生"的对立事件
是"A,B均不发生".
(2)AB=AUB
意义:"A,B均发生"的对立事件是"A,B
至少有一个不发生".
4.对偶律(De Morgan定理)
知识讲解
例1 设A,B为随机事件,证明
(1)
(2)
证 (1)
知识讲解
(2) A+BA=AUBA
=(AUB)(AUA)
=(AUB)Ω=AUB
AB+AB+ AB
=A(B+B)+ AB=AΩ+ BA = A+ BA=AUB
归纳方法
(1)包含关系、相等关系的判定①事件的包含关系与集合的包含关系相似;②两事件相等的实质为相同事件,即同时发生或同时不发生.(2)判断事件是否互斥的两个步骤第一步,确定每个事件包含的结果;第二步,确定是否有一个结果发生会意味着两个事件都发生,若是,则两个事件不互斥,否则就是互斥的.(3)判断事件是否对立的两个步骤第一步,判断是互斥事件;第二步,确定两个事件必然有一个发生,否则只有互斥,但不对立.
练习
判断下列给出的每对事件,是否为互斥事件,是否为对立事件,并说明理由.从40张扑克牌(红桃、黑桃、方块、梅花点数从1~10各10张)中,任取1张.(1)“抽出红桃”与“抽出黑桃”;(2)“抽出红色牌”与“抽出黑色牌”;(3)“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”.
练习
解:(1)是互斥事件,不是对立事件.理由是从40张扑克牌中任意抽取1张,“抽出红桃”和“抽出黑桃”是不可能同时发生的,所以是互斥事件.同时,不能保证其中必有一个发生,这是由于还可能抽出“方块”或者“梅花”,因此,二者不是对立事件.(2)既是互斥事件,又是对立事件.理由是从40张扑克牌中,任意抽取1张,“抽出红色牌”与“抽出黑色牌”两个事件不可能同时发生,且其中必有一个发生,所以它们既是互斥事件,又是对立事件.
练习
(3)不是互斥事件,也不是对立事件.理由是从40张扑克牌中任意抽取1张,“抽出的牌点数为5的倍数”与“抽出的牌点数大于9”这两个事件可能同时发生,如抽得点数为10,因此,二者不是互斥事件,当然也不可能是对立事件.
知识拓展
例1 设A,B,C为三个事件,试用这三个事
件的运算关系表示下列事件:
(1)A发生,而B,C都不发生.
可表示为:ABC,或 ABUC;
(2)A,B都发生,C不发生;
ABC,或AB-C;
(3)三个事件同时都发生; ABC;
(4)A,B,C中恰有一个事件发生可表示为: ABC+ABC+ABC;
知识拓展
(5)A,B,C中恰有两个发生可表
示为: ABC+ABC+ABC,
或ABUBCUAC-ABC;
(6)三个事件至少有一个发生;
AUBUC.
知识拓展
例3 设A,B为随机事件,证明:
(1) A-B=A-AB,
(2)AUB=A+BA=AB+ AB+ AB.
证 (1)A-AB=AAB (A-B=AB)
=A(AUB)
=AAUAB= UAB =AB=A-B.
知识拓展
(2) A+BA=AUBA
=(AUB)(AUA)
=(AUB)Ω=AUB.
AB+AB+ AB
=A(B+B)+AB=AΩ+BA =A+BA=AUB.
小结
二、小结
1.随机事件间的关系(六种)
2.事件间的运算规律(四种)
3.概率论与集合论之间术语的对应关系
(见下表)
小结
概率论与集合论之间的对应关系
记号 概率论 集合论
样本空间,必然事件 不可能事件 基本事件 随机事件 A的对立事件 A发生必然导致B发生 事件A与事件B相等 空间(全集)
空集
元素
子集
A的补集
A是B的子集
A集合与B集合相等
小结
AUB 事件A与事件B的和 A集合与B集合的并集
AB 事件A与B的积事件 A集合与B集合的交集
A-B 事件A与事件B的差 A与B两集合的差集
AB= 事件A与B互不相容 A与B两集合中没有相同的元素
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
