4.12角平分线课件(北京课改版七年级上)
文档属性
| 名称 | 4.12角平分线课件(北京课改版七年级上) |

|
|
| 格式 | rar | ||
| 文件大小 | 263.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 京教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2009-08-19 00:00:00 | ||
图片预览








文档简介
课件22张PPT。探索角平分线角平分线的教学设计教学目标教学手段及方法教学过程的设计《角平分线》简介探索教学重点和难点一、教学目标:教学目标1.理解角平分线的意义. 探索2.熟练掌握角平分线的三种
表示方法. 3.初步培养学生运用类比的
方法研究问题的意识 .教学重点二、教学重难点: 角平分线的概念和三种表示方法 .探索教学难点二、教学重难点:探索 恰当的运用角平分线的三种表示方法进行简单的推理计算.三、教学手段、教学方法: 教学手段、方法合作探究与启发引导相结合 探索计算机、量角器、三角板.四、教学过程:类比引入阶段 ;探究新知阶段 ;巩固应用阶段 ; 教学总结.四个阶段探索四、教学过程:类比引入阶段
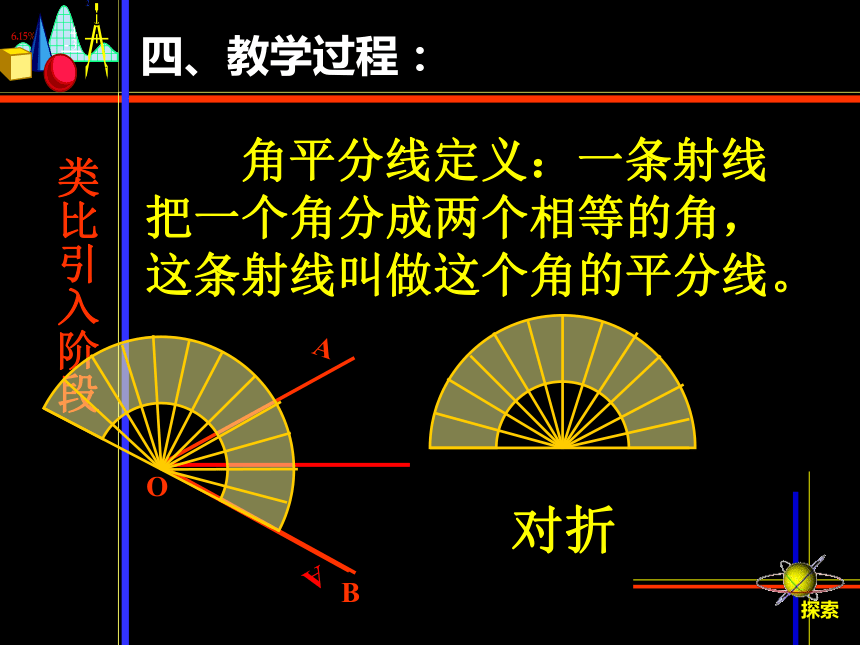
探索四、教学过程:类比引入阶段探索 角平分线定义:一条射线 把一个角分成两个相等的角, 这条射线叫做这个角的平分线。OB 对折 四、教学过程:探究新知阶段 剖析概念 1.角平分线是一条射线,由 角的顶点引出的一条射线; 探索2.这条射线把角分成两个相 等的角. 四、教学过程:探究新知阶段 小组活动探索C四、教学过程:综合应用阶段探索抢答练习 练习1.如图,OC是∠AOE的平分线,则
(1) ∠AOC= ;∠AOE=2 ; ∠AOC= ;四、教学过程:综合应用阶段探索 变式1:如图,当∠AOE为平角,其它条件不变时,你能说出∠BOD的度数吗? 变式2:若OC是任一条射线,OB是∠AOC的平分线,OD是∠EOC的平分线,那么上述结论会改变吗?四、教学过程:综合应用阶段探索练习2:如图:OC是AOB的角平分线,
∠CAO = 90 ,∠COB = 90,比较
∠ACO与∠BCO的大小。四、教学过程:综合应用阶段探索练习3:如图,∠AOB=∠BOC=∠COD,则∠AOC的平分线是 ,∠BOD的平分线是 ,∠AOD的三等分线是 ,3∠BOC=∠ , ∠AOD= = = 。四、教学过程:综合应用阶段探索 例.已知:如图,∠AOB=160°,OC为∠AOB的平分线,OD为∠COB的平分线,求∠COD的度数。变式:若已知OC为∠AOB的平分线,OD为∠COB的平分线,∠COD=40°,则∠AOB的度数是多少?
探索题:
如图,已知:∠AOB=90°,∠AOC是60°,OD平分∠BOC,OE平分∠AOC.
(1)求∠DOE;
(2)如果∠AOB=α,其它 条件不变,求∠DOE;
四、教学过程:综合应用阶段探索(3)如果把原题中的∠AOC是60°这个条件改为∠AOC是锐角,你能否求出∠DOE?若能,请你说出来;若不能,请说明理由.
(4)从以上结果中能得到什么结论?
四、教学过程:综合应用阶段探索(5)线段的计算与角的计算存在着密切的关系,他们之间可以互相借鉴解法,请你模仿此例,设计一道以线段为背景的计算题,写出其中的规律,并给出解答. 四、教学过程:综合应用阶段探索四、教学过程:综合应用阶段探索拓展延伸,思维训练 利用三角板观察、猜想,归纳出角平分线性质:角平分线上的点到角两边的距离相等. 四、教学过程:教学总结探索本节课学习了哪些知识?你有哪些收获?你认为需要注意什么?
谢谢大家再见
探索四、教学过程:类比引入阶段探索 角平分线定义:一条射线 把一个角分成两个相等的角, 这条射线叫做这个角的平分线。OB 对折 四、教学过程:探究新知阶段 剖析概念 1.角平分线是一条射线,由 角的顶点引出的一条射线; 探索2.这条射线把角分成两个相 等的角. 四、教学过程:探究新知阶段 小组活动探索C四、教学过程:综合应用阶段探索抢答练习 练习1.如图,OC是∠AOE的平分线,则
(1) ∠AOC= ;∠AOE=2 ; ∠AOC= ;四、教学过程:综合应用阶段探索 变式1:如图,当∠AOE为平角,其它条件不变时,你能说出∠BOD的度数吗? 变式2:若OC是任一条射线,OB是∠AOC的平分线,OD是∠EOC的平分线,那么上述结论会改变吗?四、教学过程:综合应用阶段探索练习2:如图:OC是AOB的角平分线,
∠CAO = 90 ,∠COB = 90,比较
∠ACO与∠BCO的大小。四、教学过程:综合应用阶段探索练习3:如图,∠AOB=∠BOC=∠COD,则∠AOC的平分线是 ,∠BOD的平分线是 ,∠AOD的三等分线是 ,3∠BOC=∠ , ∠AOD= = = 。四、教学过程:综合应用阶段探索 例.已知:如图,∠AOB=160°,OC为∠AOB的平分线,OD为∠COB的平分线,求∠COD的度数。变式:若已知OC为∠AOB的平分线,OD为∠COB的平分线,∠COD=40°,则∠AOB的度数是多少?
探索题:
如图,已知:∠AOB=90°,∠AOC是60°,OD平分∠BOC,OE平分∠AOC.
(1)求∠DOE;
(2)如果∠AOB=α,其它 条件不变,求∠DOE;
四、教学过程:综合应用阶段探索(3)如果把原题中的∠AOC是60°这个条件改为∠AOC是锐角,你能否求出∠DOE?若能,请你说出来;若不能,请说明理由.
(4)从以上结果中能得到什么结论?
四、教学过程:综合应用阶段探索(5)线段的计算与角的计算存在着密切的关系,他们之间可以互相借鉴解法,请你模仿此例,设计一道以线段为背景的计算题,写出其中的规律,并给出解答. 四、教学过程:综合应用阶段探索四、教学过程:综合应用阶段探索拓展延伸,思维训练 利用三角板观察、猜想,归纳出角平分线性质:角平分线上的点到角两边的距离相等. 四、教学过程:教学总结探索本节课学习了哪些知识?你有哪些收获?你认为需要注意什么?
谢谢大家再见
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
