人教版六年级上册数学 《圆的周长》课件(共26张PPT)
文档属性
| 名称 | 人教版六年级上册数学 《圆的周长》课件(共26张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 35.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 06:49:22 | ||
图片预览








文档简介
(共26张PPT)
人教版六年级上册第五单元第二课时
周
的
圆
长
问题一:什么是圆?
问题二:圆有什么特点?
问题三:“圆,一中同长也”指的是什么?
探索新知
思考一下,这个问题实际让我们求什么?
思考
围成圆的曲线的长是圆的周长。
1.请拿出你们准备的圆,摸一摸,找一找圆的周长在哪里?哪一部分是圆的周长?说一说什么是圆的周长?
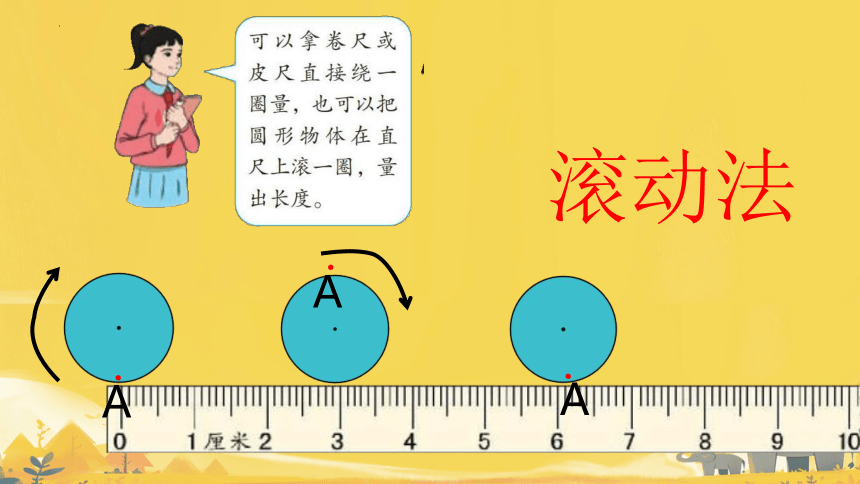
2.如何测量圆的周长呢?
A
.
A
.
A
.
滚动法
A
.
化曲为直
思考
3.圆的周长与什么有关?
圆的周长与圆的大小有关
圆的大小取决于圆的半径的长度。
找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填人下表中,看看有什么发现。
操作
周长
直径
的比值
(保留两位小数)
通过上面的表格,你发现了什么?
结论
一个圆的周长总是它的直径的3倍多一些。
它是一个无限不循环小数, π =3.1415926535……
π≈3.14
任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π(pai)表示。
约2000年前,中国古代数学著作《周髀算经》中就有“周三径一”的说法,意思是说圆的周长是它直径的3倍。
约1500年前,中国伟大的数学加和天文学家祖冲之计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到小数点后第7位的人。这一成就比国外大约早1000年。现在人们用计算机算出的圆周率,小数点后面已经超过万亿位。
探究新知
总结圆的周长公式:
用字母表示计算周长的公式(用C 表示圆的周长):
C = πd
C = 2πr
周长=π×直径
周长= 2×π×半径
圆的一周是曲线,曲线测量很艰难。
绕线滚动可测量,化曲为直变简单。
周长直径商不变,圆周率π到眼前。
乘除关系变一变,周长公式便出现。
已知条件:
(1)自行车轮子的半径大约是33cm。
(2)小明家离学校1km。
所求问题:
(1)自行车轮子转1圈,大约可以走多远?
(2)小明家到学校,轮子大约转多少圈?
例1:小明的自行车轮子的半径大约是33cm。这两自行车轮子转1圈,大约可以走多远?(结果保留整米数)小明家离学校1km,骑车从家到学校,轮子大约转了多少圈?
例1:小明的自行车轮子的半径大约是33cm。这两自行车轮子转1圈,大约可以走多远?(结果保留整米数)小明家离学校1km,骑车从家到学校,轮子大约转了多少圈?
1000÷2=500(圈)
1 km=1000 m
C=2πr
探究新知
=2×3.14×33
=207.24(cm)
≈ 2(m)
答:这两自行车轮子转1圈,大约可以走2米;骑车从家到学校,轮子大约转了500圈。
趣味分类
求下面各圆的周长。
C=2πr
C=πd
C=2πr
[教材P62 做一做第1题]
课堂练习
=2×3.14×3
=18.84(cm)
=3.14×6
=18.84(cm)
=2×3.14×5
=31.4(cm)
答:这个圆桌面的直径是1.5 m。
d =C÷3.14
[教材P62 做一做第2题]
课堂练习
这个圆桌面的直径是多少?
=4.71÷3.14
=1.5(m)
一个圆形喷水池的半径是5m,它的周长是多少米?【教材63页第一题】
答:它的周长是31.4米。
C=2πr
=2×3.14×5
=31.4(m)
一个古代建筑中大红圆柱横截面的周长是3.14m。这个圆柱横截面的直径是多少米?
答:这个圆柱横截面的直径是1米.
d=C ÷ π
=3.14÷3.14
=1(米)
【教材63页第三题】
知识拓展:
由C=πd 可知,圆的半径或直径扩大到原来的几倍,它的周长也扩大到原来的几倍;圆的半径或直径缩小到原来的几分之一,它的周长也缩小到原来的几分之一。
回顾今天所学内容,完成填空。
课堂总结
你知道吗
数学之美
人教版六年级上册第五单元第二课时
周
的
圆
长
问题一:什么是圆?
问题二:圆有什么特点?
问题三:“圆,一中同长也”指的是什么?
探索新知
思考一下,这个问题实际让我们求什么?
思考
围成圆的曲线的长是圆的周长。
1.请拿出你们准备的圆,摸一摸,找一找圆的周长在哪里?哪一部分是圆的周长?说一说什么是圆的周长?
2.如何测量圆的周长呢?
A
.
A
.
A
.
滚动法
A
.
化曲为直
思考
3.圆的周长与什么有关?
圆的周长与圆的大小有关
圆的大小取决于圆的半径的长度。
找一些圆形的物品,分别量出它们的周长和直径,并算出周长和直径的比值,把结果填人下表中,看看有什么发现。
操作
周长
直径
的比值
(保留两位小数)
通过上面的表格,你发现了什么?
结论
一个圆的周长总是它的直径的3倍多一些。
它是一个无限不循环小数, π =3.1415926535……
π≈3.14
任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母π(pai)表示。
约2000年前,中国古代数学著作《周髀算经》中就有“周三径一”的说法,意思是说圆的周长是它直径的3倍。
约1500年前,中国伟大的数学加和天文学家祖冲之计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到小数点后第7位的人。这一成就比国外大约早1000年。现在人们用计算机算出的圆周率,小数点后面已经超过万亿位。
探究新知
总结圆的周长公式:
用字母表示计算周长的公式(用C 表示圆的周长):
C = πd
C = 2πr
周长=π×直径
周长= 2×π×半径
圆的一周是曲线,曲线测量很艰难。
绕线滚动可测量,化曲为直变简单。
周长直径商不变,圆周率π到眼前。
乘除关系变一变,周长公式便出现。
已知条件:
(1)自行车轮子的半径大约是33cm。
(2)小明家离学校1km。
所求问题:
(1)自行车轮子转1圈,大约可以走多远?
(2)小明家到学校,轮子大约转多少圈?
例1:小明的自行车轮子的半径大约是33cm。这两自行车轮子转1圈,大约可以走多远?(结果保留整米数)小明家离学校1km,骑车从家到学校,轮子大约转了多少圈?
例1:小明的自行车轮子的半径大约是33cm。这两自行车轮子转1圈,大约可以走多远?(结果保留整米数)小明家离学校1km,骑车从家到学校,轮子大约转了多少圈?
1000÷2=500(圈)
1 km=1000 m
C=2πr
探究新知
=2×3.14×33
=207.24(cm)
≈ 2(m)
答:这两自行车轮子转1圈,大约可以走2米;骑车从家到学校,轮子大约转了500圈。
趣味分类
求下面各圆的周长。
C=2πr
C=πd
C=2πr
[教材P62 做一做第1题]
课堂练习
=2×3.14×3
=18.84(cm)
=3.14×6
=18.84(cm)
=2×3.14×5
=31.4(cm)
答:这个圆桌面的直径是1.5 m。
d =C÷3.14
[教材P62 做一做第2题]
课堂练习
这个圆桌面的直径是多少?
=4.71÷3.14
=1.5(m)
一个圆形喷水池的半径是5m,它的周长是多少米?【教材63页第一题】
答:它的周长是31.4米。
C=2πr
=2×3.14×5
=31.4(m)
一个古代建筑中大红圆柱横截面的周长是3.14m。这个圆柱横截面的直径是多少米?
答:这个圆柱横截面的直径是1米.
d=C ÷ π
=3.14÷3.14
=1(米)
【教材63页第三题】
知识拓展:
由C=πd 可知,圆的半径或直径扩大到原来的几倍,它的周长也扩大到原来的几倍;圆的半径或直径缩小到原来的几分之一,它的周长也缩小到原来的几分之一。
回顾今天所学内容,完成填空。
课堂总结
你知道吗
数学之美
