人教版六年级上册数学 《圆的周长》(课件)(共15张PPT)
文档属性
| 名称 | 人教版六年级上册数学 《圆的周长》(课件)(共15张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 06:48:13 | ||
图片预览






文档简介
(共15张PPT)
圆的周长
圆桌和菜板都有点开裂,需要在他们的边缘围上一圈铁皮。
分别需要多长的铁皮啊?
情景导入
求需要多长铁皮是求什么么?
像这样,围成圆的曲线的长是圆的周长。
交流讨论:怎样求一个圆的周长?
可以把圆形物体在直尺上滚一圈,量出长度
A
.
A
.
A
.
滚动法
A
.
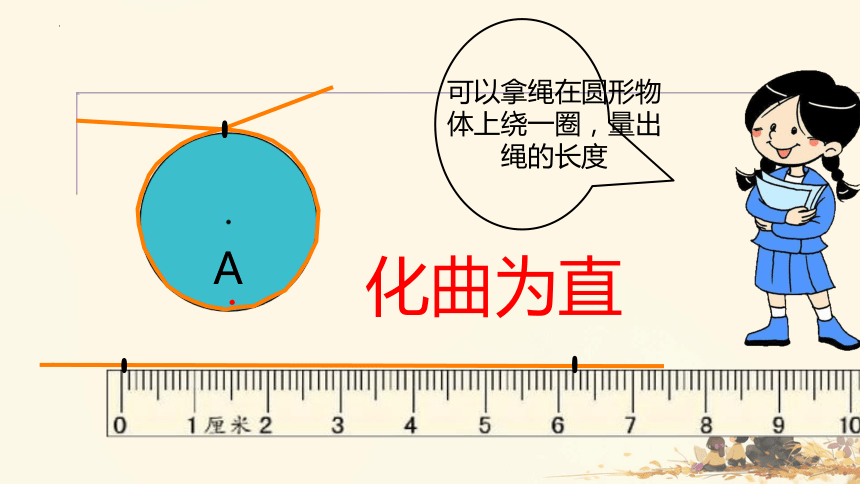
可以拿绳在圆形物体上绕一圈,量出绳的长度
化曲为直
除了上面的方法,还可以怎样求圆的周长呢?
讨论:
让我们一起来做一个实验:找一些圆形物品分别量出它们的周长和直径,并计算出周长和直径的比值,把结果填入下表中,看看有什么发现。
(保留两位小数)
18.85
6
3.14
9.26
3
3.14
28.2
9
3.13
31.5
10
3.15
原来一个圆的周长总是直径的3倍多一些
其实,早就有人研究了圆的周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母表示。它的一个无限不循环小数, , 但在实际中常常取它的近似值,例如
如果用C表示圆的周长,就有:
或
祖冲之在数学上的重要贡献是求得了圆周率的七位小数的精确值。他所提出的圆周率的密率,比荷兰工程师安托尼兹早了1000年。因此,日本数学家三上义夫建议,把原来以安托尼兹命名的圆周率的密率,改为“祖率”,以纪念祖冲之。所谓圆周率,就是圆周长与直径长之比。圆周率通用希腊字母π表示,因为希腊文中“周围”一词的开头字母是π。求算π的值是数学上一个耐人寻味的问题,许多数学家为求算π的值花费了多年的精力。我国的数学家们研究π,很早就开始了。在公元前100多年的一部《周髀算经》里,就有“周三径一”的记载,也就是π= 3。
祖冲之算出π为3.1415926与3.1415927之间,是世界上最早的七位小数精确值。
祖冲之与圆周率
我用皮尺量的桌面的直径是1.5m。
这个圆桌需要多长的铁皮?
求下面各圆的周长。
d=6cm
r=3cm
r=3cm
r=5cm
这个圆菜板的直径是多少?
我用皮尺量的菜板的周长是125.6厘米。
今天你有什么收获?
今天你有什么收获?
圆的周长
圆桌和菜板都有点开裂,需要在他们的边缘围上一圈铁皮。
分别需要多长的铁皮啊?
情景导入
求需要多长铁皮是求什么么?
像这样,围成圆的曲线的长是圆的周长。
交流讨论:怎样求一个圆的周长?
可以把圆形物体在直尺上滚一圈,量出长度
A
.
A
.
A
.
滚动法
A
.
可以拿绳在圆形物体上绕一圈,量出绳的长度
化曲为直
除了上面的方法,还可以怎样求圆的周长呢?
讨论:
让我们一起来做一个实验:找一些圆形物品分别量出它们的周长和直径,并计算出周长和直径的比值,把结果填入下表中,看看有什么发现。
(保留两位小数)
18.85
6
3.14
9.26
3
3.14
28.2
9
3.13
31.5
10
3.15
原来一个圆的周长总是直径的3倍多一些
其实,早就有人研究了圆的周长与直径的关系,发现任意一个圆的周长与它的直径的比值是一个固定的数,我们把它叫做圆周率,用字母表示。它的一个无限不循环小数, , 但在实际中常常取它的近似值,例如
如果用C表示圆的周长,就有:
或
祖冲之在数学上的重要贡献是求得了圆周率的七位小数的精确值。他所提出的圆周率的密率,比荷兰工程师安托尼兹早了1000年。因此,日本数学家三上义夫建议,把原来以安托尼兹命名的圆周率的密率,改为“祖率”,以纪念祖冲之。所谓圆周率,就是圆周长与直径长之比。圆周率通用希腊字母π表示,因为希腊文中“周围”一词的开头字母是π。求算π的值是数学上一个耐人寻味的问题,许多数学家为求算π的值花费了多年的精力。我国的数学家们研究π,很早就开始了。在公元前100多年的一部《周髀算经》里,就有“周三径一”的记载,也就是π= 3。
祖冲之算出π为3.1415926与3.1415927之间,是世界上最早的七位小数精确值。
祖冲之与圆周率
我用皮尺量的桌面的直径是1.5m。
这个圆桌需要多长的铁皮?
求下面各圆的周长。
d=6cm
r=3cm
r=3cm
r=5cm
这个圆菜板的直径是多少?
我用皮尺量的菜板的周长是125.6厘米。
今天你有什么收获?
今天你有什么收获?
