北师大版四年级数学上册四 运算律(课件)(共22张PPT)
文档属性
| 名称 | 北师大版四年级数学上册四 运算律(课件)(共22张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 8.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 07:51:03 | ||
图片预览






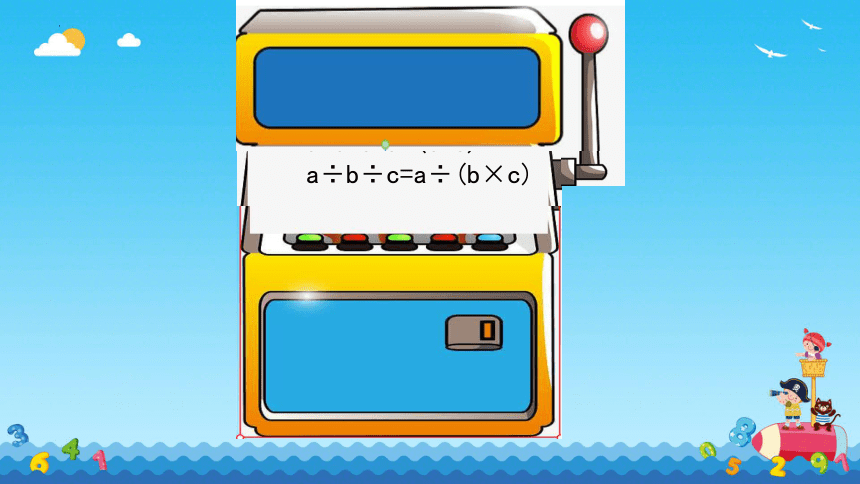
文档简介
(共22张PPT)
运算律整理与复习
北师大版 四年级上册 第四单元 运算律
a+b=b+a
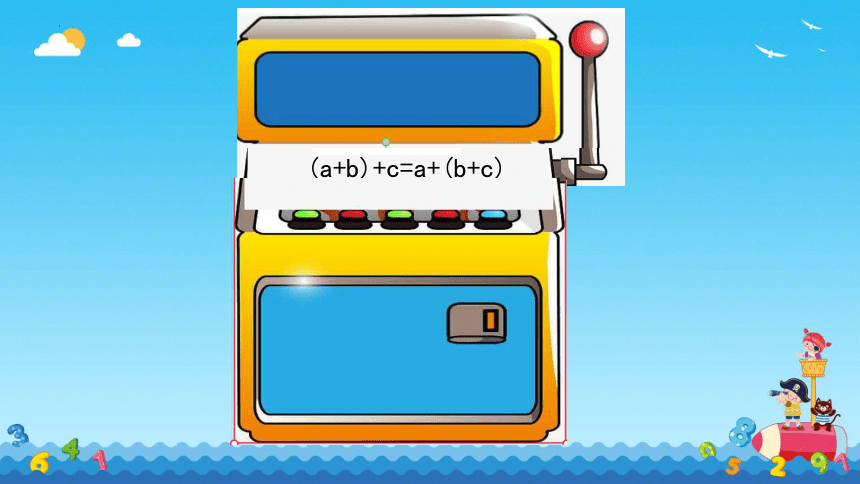
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
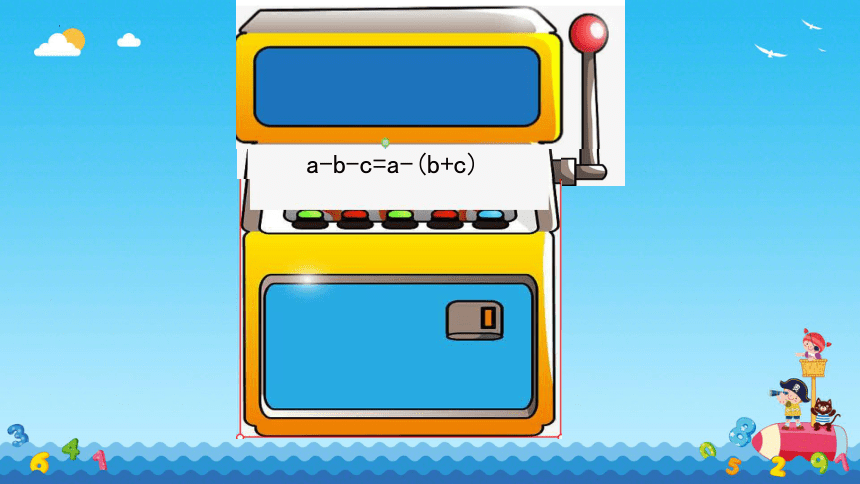
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
混合运算的运算法则
只有加、减运算,或者只有乘、除运算时,按从左到右的顺序依次计算。
a
1
1000-289+11
=711+11
=722
既有加、减运算,又有乘、除运算时,先算乘、除再算加、减。
b
176-176÷8
=176-22
=154
如果有括号,要先算小括号里面的,再算中括号里面的。
c
288-[8×(26-14)]
=288-[8×12]
=288-96
=192
2
加法运算定律
加法交换律:两个数相加,交换加数的位置,和不变。用字母表示为:
a+b= b+a。
a
加法结合律:三个数相加,先算前两个数相加或先算后两个数相加,和不变。用字母表示为:(a+b)+c=a+(b+c)。
b
乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。用字母表示为:
(a+b)×c=a×c+b×c。
c
3
两个性质
(1)一个数连续除以两个数等于这个数除以这两个数的和。用字母表示为a-b-c=a-(b+c)。
(2)一个数连续除以两个不为0的数,等于这个数除以这两个数的积。用字母表示为a÷b÷c=a÷(b×c)
加法交换律
a+b=
b+a
乘法交换律
a×b=
b×a
加法结合律
(a+b)+c=
a+(b+c)
乘法结合律
(a×b)×c=
a×(b×c)
乘法分配律
(a+b)×c=
a×c+b×c
提升练习:用简便方法计算。
28×111+999×8
=28×111+111×(9×8)
=28×111+111×72
=(28+72)×111
=100×111
=111000
999
运算律整理与复习
北师大版 四年级上册 第四单元 运算律
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
a+b=b+a
(a+b)+c=a+(b+c)
a×b=b×a
(a×b)×c=a×(b×c)
(a+b)×c=a×c+b×c
a-b-c=a-(b+c)
a÷b÷c=a÷(b×c)
混合运算的运算法则
只有加、减运算,或者只有乘、除运算时,按从左到右的顺序依次计算。
a
1
1000-289+11
=711+11
=722
既有加、减运算,又有乘、除运算时,先算乘、除再算加、减。
b
176-176÷8
=176-22
=154
如果有括号,要先算小括号里面的,再算中括号里面的。
c
288-[8×(26-14)]
=288-[8×12]
=288-96
=192
2
加法运算定律
加法交换律:两个数相加,交换加数的位置,和不变。用字母表示为:
a+b= b+a。
a
加法结合律:三个数相加,先算前两个数相加或先算后两个数相加,和不变。用字母表示为:(a+b)+c=a+(b+c)。
b
乘法分配律:两个数的和与一个数相乘,可以先把它们分别与这个数相乘,再相加。用字母表示为:
(a+b)×c=a×c+b×c。
c
3
两个性质
(1)一个数连续除以两个数等于这个数除以这两个数的和。用字母表示为a-b-c=a-(b+c)。
(2)一个数连续除以两个不为0的数,等于这个数除以这两个数的积。用字母表示为a÷b÷c=a÷(b×c)
加法交换律
a+b=
b+a
乘法交换律
a×b=
b×a
加法结合律
(a+b)+c=
a+(b+c)
乘法结合律
(a×b)×c=
a×(b×c)
乘法分配律
(a+b)×c=
a×c+b×c
提升练习:用简便方法计算。
28×111+999×8
=28×111+111×(9×8)
=28×111+111×72
=(28+72)×111
=100×111
=111000
999
同课章节目录
- 一 认识更大的数
- 1 数一数
- 2 认识更大的数
- 3 人口普查
- 4 国土面积
- 5 近似数
- 6 从结绳计数说起
- 二 线与角
- 1 线的认识
- 2 相交与垂直
- 3 平移与平行
- 4 旋转与角
- 5 角的度量(一)
- 6 角的度量(二)
- 三 乘法
- 1 卫星运行时间
- 2 有多少名观众
- 3 神奇的计算工具
- 4 有趣的算式
- 四 运算律
- 1 买文具
- 2 加法交换律和乘法交换律
- 3 加法结合律
- 4 乘法结合律
- 5 乘法分配律
- 五 方向与位置
- 1 去图书馆
- 2 确定位置
- 六 除法
- 1 买文具
- 2 参观花圃
- 3 秋游
- 4 商不变的规律
- 5 路程、时间与速度
- 七 生活中的负数
- 1 温度
- 2 正负数
- 数学好玩
- 1 滴水试验
- 2 编码
- 3 数图形的学问
- 八 可能性
- 1 不确定性
- 2 摸球游戏
