20.1.2中位数和众数 巩固练习(含简单答案) 2023-2024学年人教版八年级数学下册
文档属性
| 名称 | 20.1.2中位数和众数 巩固练习(含简单答案) 2023-2024学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 263.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 09:24:17 | ||
图片预览


文档简介
20.1.2中位数和众数
一、单选题
1.某班第一小组7名同学的毕业升学体育测试成绩(满分50分)依次为:48,46,47,48,48,50,49,这组数据的众数分别是( )
A.47 B.48 C.49 D.50
2.有一组数据:2,1,3,5,,6,它的平均数是3,则这组数据的中位数是( )
A.1 B.2 C.2.5 D.3
3.某班班主任调查了本班学生一周的居家体育锻炼时间,统计数据如下表所示:
时间(小时) 7 8 9 10 11
人数(人) 8 5 7 12 8
则该班学生一周的居家体育锻炼时间的中位数和众数分别是( )
A.9,10 B.9.5,10 C.10,10 D.9.5,11
4.若一组数据2,2,x,5,7,7的众数为7,则这组数据的x为( )
A.2 B.5 C.6 D.7
5.某校男篮队员的年龄分布如表所示:
年龄/岁 13 14 15
人数 a 4﹣a 6
对于不同的a,下列关于年龄的统计量不会发生改变的是( )
A.平均数,中位数 B.众数,中位数 C.众数,方差 D.平均数,方差
6.某公司5名员工在一次义务募捐中的捐款额为(单位:元):30,40,50,60,60.若捐款最少的员工又多捐了30元,则分析这5名员工捐款额的数据时,不受影响的统计量是( )
A.众数 B.中位数 C.平均数 D.极差
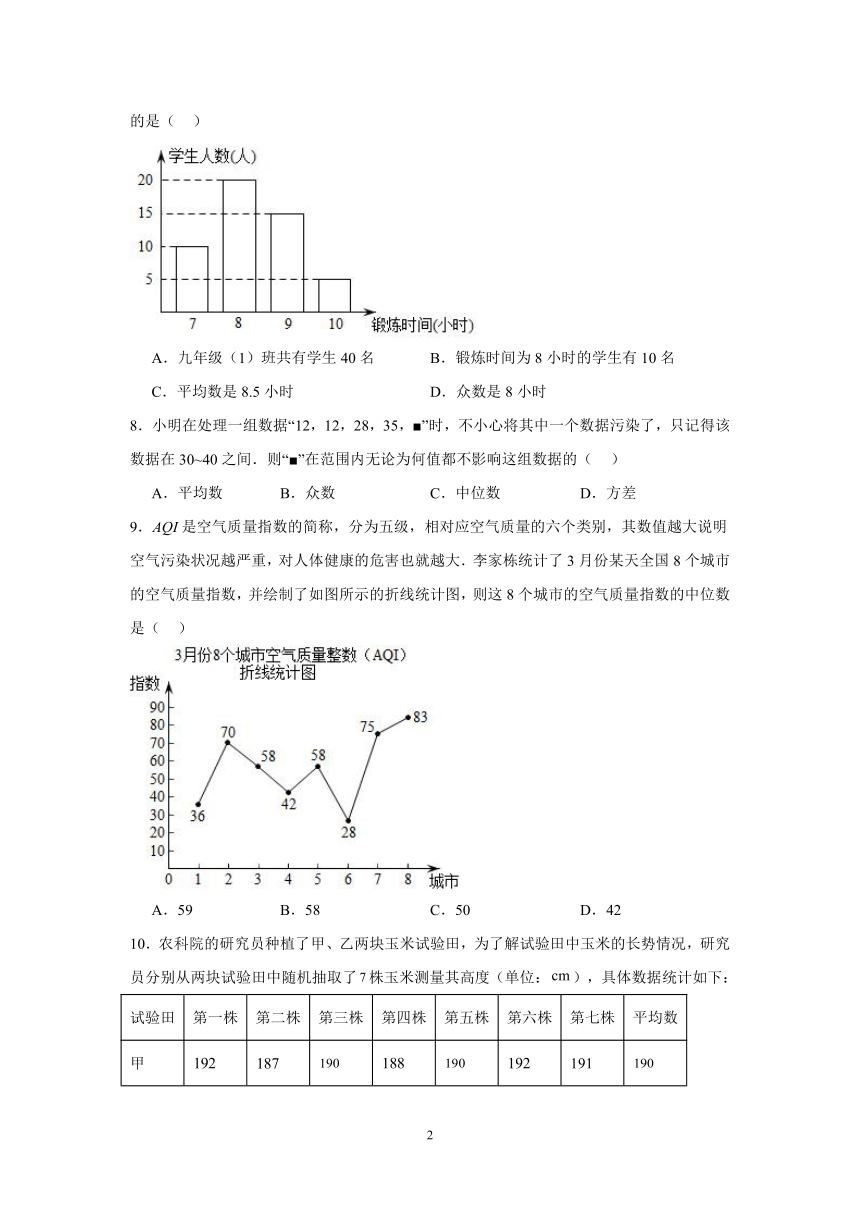
7.为了解学生参加体育锻炼的情况、现将九年级(1)班同学一周的体育锻炼情况绘制成如图所示不完整的条形统计图,已知锻炼7小时的人数占全班总人数的20%,则下列结论正确的是( )
A.九年级(1)班共有学生40名 B.锻炼时间为8小时的学生有10名
C.平均数是8.5小时 D.众数是8小时
8.小明在处理一组数据“12,12,28,35,■”时,不小心将其中一个数据污染了,只记得该数据在30~40之间.则“■”在范围内无论为何值都不影响这组数据的( )
A.平均数 B.众数 C.中位数 D.方差
9.AQI是空气质量指数的简称,分为五级,相对应空气质量的六个类别,其数值越大说明空气污染状况越严重,对人体健康的危害也就越大.李家栋统计了3月份某天全国8个城市的空气质量指数,并绘制了如图所示的折线统计图,则这8个城市的空气质量指数的中位数是( )
A.59 B.58 C.50 D.42
10.农科院的研究员种植了甲、乙两块玉米试验田,为了解试验田中玉米的长势情况,研究员分别从两块试验田中随机抽取了株玉米测量其高度(单位:),具体数据统计如下:
试验田 第一株 第二株 第三株 第四株 第五株 第六株 第七株 平均数
甲
乙
根据测量数据,长势比较整体的是( )
A.甲试验田 B.乙试验田 C.两块试验田一样 D.无法判断
二、填空题
11.“大美丹东,大爱无疆”,在为青海玉树的捐款活动中,某小组7位同学的捐款数额(元)分别是:5,20,5,50,10,5,10,则这组数据的中位数是 .
12.某次数学测验中,五位同学的分数分别是:89,91,105,105,110,这组数据的中位数是 ,众数是 ,平均数是
13.从小到大排列的一组数,如果这组数据的平均数与中位数相等,则的值为 .
14.已知一个样本1、a、3、4、7,它的平均数是4,则这个样本的标准差是 .
15.小明连续5天的体温数据如下(单位:):,,,,,这组数据的极差是 .
16.已知一个样本有50个数据,其中最大值为83,最小值为32,若取组距为10,则应把它分成 组.
三、解答题
17.逸翠园中学八年级全体同学参加了某项捐款活动,随机抽取了部分同学捐款的情况进行统计,并绘制了两幅不完整统计图.
(1)求本次共抽查学生的人数,并将条形统计图补充完整;
(2)捐款金额的平均数是_______,中位数是_______;
(3)请你估算八年级800名学生中捐款大于等于20元的学生人数.
18.随着人们饮食结构愈发复杂,囤鲜需求与日俱增,为满足用户不同需求,某品牌推出了甲、乙两种型号的冰箱在商场中进行试销售,如图是根据甲、乙两种型号冰箱的销售量绘制成的折线统计图和统计分析表(结果保留一位小数).
型号 平均数 中位数 众数 方差
甲
乙
根据以上信息,解答下列问题:
(1)填空: , ;
(2)求乙型号冰箱销售量的平均数;
(3)若该品牌计划从甲、乙两种型号的冰箱选择一种在该商场进行销售,请运用你所学的统计知识,帮助该品牌分析应该选择哪种型号的冰箱,请说明理由.
19.为迎接国庆,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表.
分数段 频数 频率
30 0.15
0.45
60
20 0.1
请根据以上图表提供的信息,解答下列问题:
(1)求表中和所表示的数,并补全频数分布直方图;
(2)请根据图表信息写出比赛成绩的中位数落在哪个分数段?
(3)若该校共有3600名学生,且规定比赛成绩80分以上(含80分)可以获得奖励,请根据上述调查结果估计该校,那么全校共有多少学生获奖?
20.为提高居民防范电信诈骗意识,确保反诈宣传工作落地见效,某社区举行《2024年防诈骗知识》竞赛,社区管理员随机从甲、乙两个小区各抽取20份答卷,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:85 80 95 100 90 95 85 65 75 85 89 90 70 90 100 80 80 90 96 75
乙小区:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据
成绩x(分)
甲小区 2 5 8 5
乙小区 3 7 5 5
分析数据
统计量 平均数 中位数 众数
甲小区 85.75 87 a
乙小区 83.5 b 80
(1)填空:a= ,b= ;
(2)若甲小区共有1000人参与答卷,请估计甲小区成绩大于80分的人数;
(3)根据以上数据分析,你认为甲、乙两个小区哪一个对防诈骗知识掌握更好?请写出其中一个理由.
参考答案:
1.B
2.C
3.B
4.D
5.B
6.A
7.D
8.C
9.B
10.A
11.10
12. 105 105 100
13.8
14.
15.
16.6/六
17.(1)人(2)13.1元,12.5元.(3)人
18.(1),(2)台
(3)建议该品牌选择乙型号的冰箱在该商场进行销售
19.(1)
(2)
(3)1440人
20.(1)90,82.5
(2)估计甲小区成绩大于80分的人数为650人
(3)甲小区的居民对防诈骗知识掌握更好
一、单选题
1.某班第一小组7名同学的毕业升学体育测试成绩(满分50分)依次为:48,46,47,48,48,50,49,这组数据的众数分别是( )
A.47 B.48 C.49 D.50
2.有一组数据:2,1,3,5,,6,它的平均数是3,则这组数据的中位数是( )
A.1 B.2 C.2.5 D.3
3.某班班主任调查了本班学生一周的居家体育锻炼时间,统计数据如下表所示:
时间(小时) 7 8 9 10 11
人数(人) 8 5 7 12 8
则该班学生一周的居家体育锻炼时间的中位数和众数分别是( )
A.9,10 B.9.5,10 C.10,10 D.9.5,11
4.若一组数据2,2,x,5,7,7的众数为7,则这组数据的x为( )
A.2 B.5 C.6 D.7
5.某校男篮队员的年龄分布如表所示:
年龄/岁 13 14 15
人数 a 4﹣a 6
对于不同的a,下列关于年龄的统计量不会发生改变的是( )
A.平均数,中位数 B.众数,中位数 C.众数,方差 D.平均数,方差
6.某公司5名员工在一次义务募捐中的捐款额为(单位:元):30,40,50,60,60.若捐款最少的员工又多捐了30元,则分析这5名员工捐款额的数据时,不受影响的统计量是( )
A.众数 B.中位数 C.平均数 D.极差
7.为了解学生参加体育锻炼的情况、现将九年级(1)班同学一周的体育锻炼情况绘制成如图所示不完整的条形统计图,已知锻炼7小时的人数占全班总人数的20%,则下列结论正确的是( )
A.九年级(1)班共有学生40名 B.锻炼时间为8小时的学生有10名
C.平均数是8.5小时 D.众数是8小时
8.小明在处理一组数据“12,12,28,35,■”时,不小心将其中一个数据污染了,只记得该数据在30~40之间.则“■”在范围内无论为何值都不影响这组数据的( )
A.平均数 B.众数 C.中位数 D.方差
9.AQI是空气质量指数的简称,分为五级,相对应空气质量的六个类别,其数值越大说明空气污染状况越严重,对人体健康的危害也就越大.李家栋统计了3月份某天全国8个城市的空气质量指数,并绘制了如图所示的折线统计图,则这8个城市的空气质量指数的中位数是( )
A.59 B.58 C.50 D.42
10.农科院的研究员种植了甲、乙两块玉米试验田,为了解试验田中玉米的长势情况,研究员分别从两块试验田中随机抽取了株玉米测量其高度(单位:),具体数据统计如下:
试验田 第一株 第二株 第三株 第四株 第五株 第六株 第七株 平均数
甲
乙
根据测量数据,长势比较整体的是( )
A.甲试验田 B.乙试验田 C.两块试验田一样 D.无法判断
二、填空题
11.“大美丹东,大爱无疆”,在为青海玉树的捐款活动中,某小组7位同学的捐款数额(元)分别是:5,20,5,50,10,5,10,则这组数据的中位数是 .
12.某次数学测验中,五位同学的分数分别是:89,91,105,105,110,这组数据的中位数是 ,众数是 ,平均数是
13.从小到大排列的一组数,如果这组数据的平均数与中位数相等,则的值为 .
14.已知一个样本1、a、3、4、7,它的平均数是4,则这个样本的标准差是 .
15.小明连续5天的体温数据如下(单位:):,,,,,这组数据的极差是 .
16.已知一个样本有50个数据,其中最大值为83,最小值为32,若取组距为10,则应把它分成 组.
三、解答题
17.逸翠园中学八年级全体同学参加了某项捐款活动,随机抽取了部分同学捐款的情况进行统计,并绘制了两幅不完整统计图.
(1)求本次共抽查学生的人数,并将条形统计图补充完整;
(2)捐款金额的平均数是_______,中位数是_______;
(3)请你估算八年级800名学生中捐款大于等于20元的学生人数.
18.随着人们饮食结构愈发复杂,囤鲜需求与日俱增,为满足用户不同需求,某品牌推出了甲、乙两种型号的冰箱在商场中进行试销售,如图是根据甲、乙两种型号冰箱的销售量绘制成的折线统计图和统计分析表(结果保留一位小数).
型号 平均数 中位数 众数 方差
甲
乙
根据以上信息,解答下列问题:
(1)填空: , ;
(2)求乙型号冰箱销售量的平均数;
(3)若该品牌计划从甲、乙两种型号的冰箱选择一种在该商场进行销售,请运用你所学的统计知识,帮助该品牌分析应该选择哪种型号的冰箱,请说明理由.
19.为迎接国庆,某校举行以“祖国成长我成长”为主题的图片制作比赛,赛后整理参赛同学的成绩,并制作成图表.
分数段 频数 频率
30 0.15
0.45
60
20 0.1
请根据以上图表提供的信息,解答下列问题:
(1)求表中和所表示的数,并补全频数分布直方图;
(2)请根据图表信息写出比赛成绩的中位数落在哪个分数段?
(3)若该校共有3600名学生,且规定比赛成绩80分以上(含80分)可以获得奖励,请根据上述调查结果估计该校,那么全校共有多少学生获奖?
20.为提高居民防范电信诈骗意识,确保反诈宣传工作落地见效,某社区举行《2024年防诈骗知识》竞赛,社区管理员随机从甲、乙两个小区各抽取20份答卷,并对他们的成绩(单位:分)进行统计、分析,过程如下:
收集数据
甲小区:85 80 95 100 90 95 85 65 75 85 89 90 70 90 100 80 80 90 96 75
乙小区:80 60 80 95 65 100 90 85 85 80 95 75 80 90 70 80 95 75 100 90
整理数据
成绩x(分)
甲小区 2 5 8 5
乙小区 3 7 5 5
分析数据
统计量 平均数 中位数 众数
甲小区 85.75 87 a
乙小区 83.5 b 80
(1)填空:a= ,b= ;
(2)若甲小区共有1000人参与答卷,请估计甲小区成绩大于80分的人数;
(3)根据以上数据分析,你认为甲、乙两个小区哪一个对防诈骗知识掌握更好?请写出其中一个理由.
参考答案:
1.B
2.C
3.B
4.D
5.B
6.A
7.D
8.C
9.B
10.A
11.10
12. 105 105 100
13.8
14.
15.
16.6/六
17.(1)人(2)13.1元,12.5元.(3)人
18.(1),(2)台
(3)建议该品牌选择乙型号的冰箱在该商场进行销售
19.(1)
(2)
(3)1440人
20.(1)90,82.5
(2)估计甲小区成绩大于80分的人数为650人
(3)甲小区的居民对防诈骗知识掌握更好
