2023-2024学年辽宁省盘锦光正实验学校高一(下)第一次月考数学试卷(含解析)
文档属性
| 名称 | 2023-2024学年辽宁省盘锦光正实验学校高一(下)第一次月考数学试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 109.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 12:38:13 | ||
图片预览



文档简介
2023-2024学年辽宁省盘锦光正实验学校高一(下)第一次月考数学试卷
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知角的终边经过点,则( )
A. B. C. D.
2.二十四节气是中国古代订立的一种用来指导农事的补充历法,是中华民族劳动人民智慧的结晶从立春起的二十四节气依次是立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种、夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降、立冬、小雪、大雪、冬至、小寒、大寒二十四节气的对应图如图所示,从年月日谷雨节气到年月日大雪节气,圆上一点转过的弧所对圆心角的弧度数为( )
A. B. C. D.
3.在四边形中,,若,则四边形是( )
A. 菱形 B. 矩形 C. 正方形 D. 不确定
4.函数图像的对称轴方程可能是( )
A. B. C. D.
5.要得到的图象只需将的图象( )
A. 向左平移个单位 B. 向右平移个单位 C. 向左平移个单位 D. 向右平移个单位
6.已知向量,若,则( )
A. B. C. D.
7.设,,,则( )
A. B. C. D.
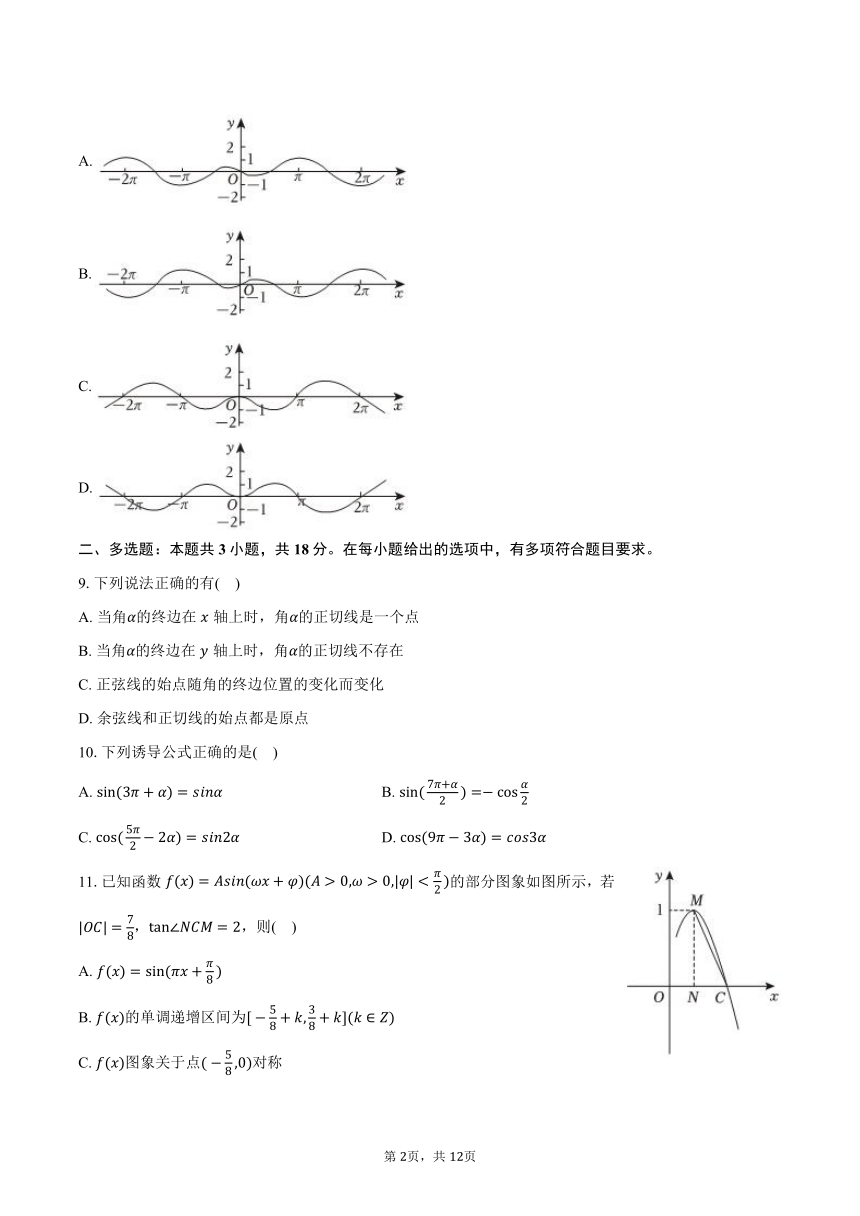
8.函数的图像大致为( )
A.
B.
C.
D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的有( )
A. 当角的终边在轴上时,角的正切线是一个点
B. 当角的终边在轴上时,角的正切线不存在
C. 正弦线的始点随角的终边位置的变化而变化
D. 余弦线和正切线的始点都是原点
10.下列诱导公式正确的是( )
A. B.
C. D.
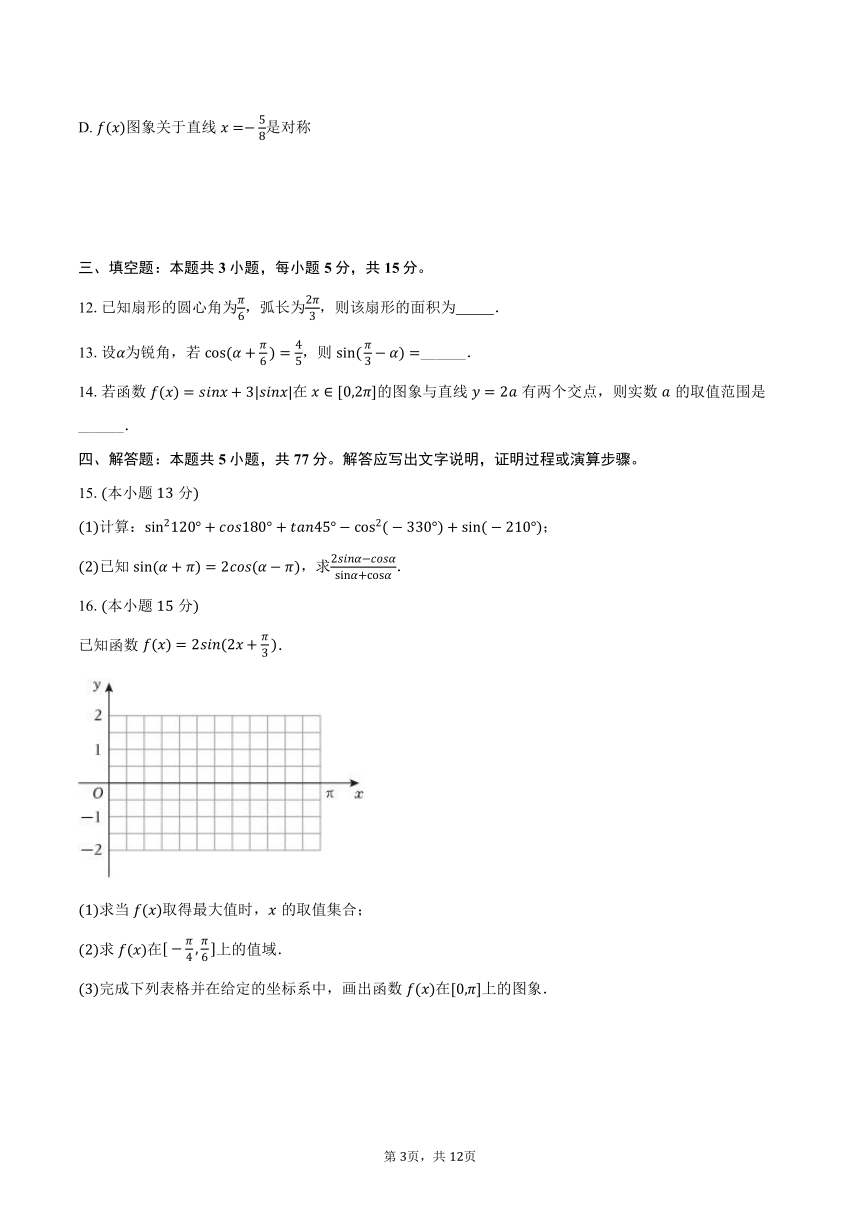
11.已知函数的部分图象如图所示,若,,则( )
A.
B. 的单调递增区间为
C. 图象关于点对称
D. 图象关于直线是对称
三、填空题:本题共3小题,每小题5分,共15分。
12.已知扇形的圆心角为,弧长为,则该扇形的面积为 .
13.设为锐角,若,则______.
14.若函数在的图象与直线有两个交点,则实数的取值范围是______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:;
已知,求.
16.本小题分
已知函数.
求当取得最大值时,的取值集合;
求在上的值域.
完成下列表格并在给定的坐标系中,画出函数在上的图象.
17.本小题分
已知.
求的值;
求的值;
求的值.
18.本小题分
近年来,我国逐渐用风能等清洁能源替代传统能源,目前利用风能发电的主要手段是风车发电如图,风车由一座塔和三个叶片组成,每两个叶片之间的夹角均为,现有一座风车,塔高米,叶片长米叶片按照逆时针方向匀速转动,并且每秒旋转一圈,风车开始旋转时某叶片的一个端点在风车的最低点此时离地面米设点转动秒后离地面的距离为米,则关于的函数关系式为.
求的解析式;
求叶片旋转一圈内点离地面的高度不低于米的时长.
19.本小题分
已知函数,的最大值是,其图象经过点.
求的解析式;
求的单调区间;
求的最值.
答案和解析
1.【答案】
【解析】解:因为角的终边经过点,
所以.
故选:.
由已知利用任意角的三角函数的定义即可求解.
本题主要考查了任意角的三角函数的定义,属于基础题.
2.【答案】
【解析】解:依题意,二十四节气将一个圆等分,所以每一份的弧度数位,
从谷雨到大雪,二十四节气圆盘需要逆时针旋转个格,
所以转过的弧所对圆心角的弧度数为.
故选:.
根据弧度制的定义计算出每一小格所代表的弧度即可得出答案.
本题主要考查了弧长公式的应用,属于基础题.
3.【答案】
【解析】解:四边形中,,
四边形为平行四边形,
又,,
四边形为矩形,
故选:.
先由判断出四边形为平行四边形,再由向量减法的几何意义将变形,进一步判断此四边形的形状.
本题主要考查了相等向量的性质,考查了向量的线性运算,属于基础题.
4.【答案】
【解析】【分析】
本题主要考查正弦函数对称轴的求法.属基础题.
令求出的值,然后根据的不同取值对选项进行验证即可.
【解析】
解:令,
,
当时,为选项,
故选D.
5.【答案】
【解析】解:将的图象向左平移个单位,得函数的图象,A正确,BCD错误.
故选:.
根据给定条件,利用图象的平移变换求解即得.
本题主要考查了三角函数图象平移变换,属于基础题.
6.【答案】
【解析】解:因为向量,
若,则,即.
故选:.
由已知结合向量平行的坐标表示即可求解.
本题主要考查了向量平行的坐标表示,属于基础题.
7.【答案】
【解析】解:,
,,
,
,
故选:.
根据三角函数的诱导公式进行转化,结合三角函数的单调性和取值范围进行比较即可.
本题主要考查三角函数值的大小比较,利用三角函数的诱导公式以及三角函数的单调性进行转化是解决本题的关键,是基础题.
8.【答案】
【解析】解:根据题意,,
其定义域为,有,则函数为奇函数,排除,
,排除.
故选:.
根据题意,先分析函数的奇偶性,排除,再计算的值,排除,综合可得答案.
本题考查函数的图象分析,涉及函数的奇偶性以及函数值符号的分析,属于基础题.
9.【答案】
【解析】解::根据三角函数线的概念,ABC正确;
:因为余弦线的始点在原点,而正切线的始点在单位圆与轴正半轴的交点上,故D错误.
故选:.
利用三角函数线的定义对各个选项逐个判断即可求解.
本题考查了三角函数线的应用,属于基础题.
10.【答案】
【解析】解:对于,,故A项错误;
对于,,故B正确;
对于,,故C正确;
对于,,故D错误.
故选:.
利用三角函数的诱导公式即可得解.
本题主要考查了诱导公式在三角函数求值中的应用,考查了转化思想,属于基础题.
11.【答案】
【解析】解:由函数的部分图象可得,
因为,,
所以,则,得.
所以,
将代入,得,
则,解得,
因为,
所以正确.
令,得错误.
,C错误,D正确.
故选:.
根据已知函数的部分图象可得,再结合函数的周期可得,然后将代入求得,即可求得函数的解析式,进而判断选项A的正误;利用三角函数的图象与性质求出函数的单调区间,即可判断选项B的正误;利用代入验证法判断函数的对称中心和对称轴即可判断选项C、的正误.
本题考查由的部分图象确定其解析式,考查运算求解能力,属于中档题.
12.【答案】
【解析】【分析】
本题考查扇形的面积、弧长公式,考查学生的计算能力,属于基础题.
利用扇形的圆心角为,弧长为,求出扇形的半径,再求扇形的面积.
【解答】
解:扇形的圆心角为,弧长为,
扇形的半径为,
扇形的面积为.
故答案为:.
13.【答案】
【解析】解:,
,
故答案为:.
由已知直接利用诱导公式化简求值.
本题考查三角函数的化简求值,考查诱导公式的应用,是基础题.
14.【答案】
【解析】解:依题意,
画出函数的图象,如图:
由图象知,当,即时,函数的图象与直线有且仅有两个不同的交点,
所以实数的取值范围是.
故答案为:.
将函数写成分段函数的形式,在同一坐标系下画出函数和函数图象,利用数形结合即可判断两函数有两个不同的交点时实数的取值范围.
本题考查三角函数的图象和性质,属于基础题.
15.【答案】解:
;
,,得,
则.
【解析】利用特殊角的三角函数值与三角函数的诱导公式即可得解;
先利用三角函数的诱导公式与基本关系式得到,再利用正余弦的齐次式法即可得解.
本题考查三角函数的化简求值,考查诱导公式及同角三角函数基本关系式的应用,是基础题.
16.【答案】解:由已知令,
则,
所以,
解得,
即当取得最大值时,的取值集合为;
当时,,
则,即
所以在上的值域为;
列表如下:
图象如下:
【解析】由已知可得,利用正弦函数的性质即可求解;
由题意可求,进而利用正弦函数的性质即可求解;
利用五点法完成表格,然后再作图即可.
本题考查了正弦函数的性质以及五点法作函数的图象,考查了函数思想,属于基础题.
17.【答案】解:由,得,
.
;
,,,则,
又,
;
由,可得.
.
【解析】两边平方,结合平方关系得由此即可进一步求解;
首先得,进一步由即可求解;
首先分别求得,,然后由商数关系即可求解.
本题考查三角函数的化简求值,考查同角三角函数的基本关系式的应用,是基础题.
18.【答案】解:如图,建立平面直角坐标系,
当时,风车开始旋转时某叶片的一个端点在风车的最低点,设为,则,
由题意得,,且,
解得,
所以;
令,则,
即,
所以,解得,
当时,,
所以叶片旋转一圈内点离地面的高度不低于米的时长为秒.
【解析】建立平面直角坐标系,根据题意列出方程组,求出,,的值,得到的解析式;
令,则,再结合正弦函数的性质求解.
本题主要考查了三角函数的应用,考查了正弦函数的图象和性质,属于中档题.
19.【答案】解:的最大值为,
,
又的图象过,
,
或,
,
,
;
由知,
由余弦函数的性质可得其增区间为,,
减区间为,;
,
令 ,,
则,,
当时,即,时,有最小值,
当时,即,时,有最大值.
【解析】根据函数的最值和过的点即可求得函数的解析式;
根据余弦函数的性质可得函数的单调区间;
换元后转化为二次函数,利用二次函数的性质求解即可.
本题考查了由的部分图象确定其解析式,余弦函数的性质以及二次函数的性质,考查了函数思想,属于中档题.
第1页,共1页
一、单选题:本题共8小题,每小题5分,共40分。在每小题给出的选项中,只有一项是符合题目要求的。
1.已知角的终边经过点,则( )
A. B. C. D.
2.二十四节气是中国古代订立的一种用来指导农事的补充历法,是中华民族劳动人民智慧的结晶从立春起的二十四节气依次是立春、雨水、惊蛰、春分、清明、谷雨、立夏、小满、芒种、夏至、小暑、大暑、立秋、处暑、白露、秋分、寒露、霜降、立冬、小雪、大雪、冬至、小寒、大寒二十四节气的对应图如图所示,从年月日谷雨节气到年月日大雪节气,圆上一点转过的弧所对圆心角的弧度数为( )
A. B. C. D.
3.在四边形中,,若,则四边形是( )
A. 菱形 B. 矩形 C. 正方形 D. 不确定
4.函数图像的对称轴方程可能是( )
A. B. C. D.
5.要得到的图象只需将的图象( )
A. 向左平移个单位 B. 向右平移个单位 C. 向左平移个单位 D. 向右平移个单位
6.已知向量,若,则( )
A. B. C. D.
7.设,,,则( )
A. B. C. D.
8.函数的图像大致为( )
A.
B.
C.
D.
二、多选题:本题共3小题,共18分。在每小题给出的选项中,有多项符合题目要求。
9.下列说法正确的有( )
A. 当角的终边在轴上时,角的正切线是一个点
B. 当角的终边在轴上时,角的正切线不存在
C. 正弦线的始点随角的终边位置的变化而变化
D. 余弦线和正切线的始点都是原点
10.下列诱导公式正确的是( )
A. B.
C. D.
11.已知函数的部分图象如图所示,若,,则( )
A.
B. 的单调递增区间为
C. 图象关于点对称
D. 图象关于直线是对称
三、填空题:本题共3小题,每小题5分,共15分。
12.已知扇形的圆心角为,弧长为,则该扇形的面积为 .
13.设为锐角,若,则______.
14.若函数在的图象与直线有两个交点,则实数的取值范围是______.
四、解答题:本题共5小题,共77分。解答应写出文字说明,证明过程或演算步骤。
15.本小题分
计算:;
已知,求.
16.本小题分
已知函数.
求当取得最大值时,的取值集合;
求在上的值域.
完成下列表格并在给定的坐标系中,画出函数在上的图象.
17.本小题分
已知.
求的值;
求的值;
求的值.
18.本小题分
近年来,我国逐渐用风能等清洁能源替代传统能源,目前利用风能发电的主要手段是风车发电如图,风车由一座塔和三个叶片组成,每两个叶片之间的夹角均为,现有一座风车,塔高米,叶片长米叶片按照逆时针方向匀速转动,并且每秒旋转一圈,风车开始旋转时某叶片的一个端点在风车的最低点此时离地面米设点转动秒后离地面的距离为米,则关于的函数关系式为.
求的解析式;
求叶片旋转一圈内点离地面的高度不低于米的时长.
19.本小题分
已知函数,的最大值是,其图象经过点.
求的解析式;
求的单调区间;
求的最值.
答案和解析
1.【答案】
【解析】解:因为角的终边经过点,
所以.
故选:.
由已知利用任意角的三角函数的定义即可求解.
本题主要考查了任意角的三角函数的定义,属于基础题.
2.【答案】
【解析】解:依题意,二十四节气将一个圆等分,所以每一份的弧度数位,
从谷雨到大雪,二十四节气圆盘需要逆时针旋转个格,
所以转过的弧所对圆心角的弧度数为.
故选:.
根据弧度制的定义计算出每一小格所代表的弧度即可得出答案.
本题主要考查了弧长公式的应用,属于基础题.
3.【答案】
【解析】解:四边形中,,
四边形为平行四边形,
又,,
四边形为矩形,
故选:.
先由判断出四边形为平行四边形,再由向量减法的几何意义将变形,进一步判断此四边形的形状.
本题主要考查了相等向量的性质,考查了向量的线性运算,属于基础题.
4.【答案】
【解析】【分析】
本题主要考查正弦函数对称轴的求法.属基础题.
令求出的值,然后根据的不同取值对选项进行验证即可.
【解析】
解:令,
,
当时,为选项,
故选D.
5.【答案】
【解析】解:将的图象向左平移个单位,得函数的图象,A正确,BCD错误.
故选:.
根据给定条件,利用图象的平移变换求解即得.
本题主要考查了三角函数图象平移变换,属于基础题.
6.【答案】
【解析】解:因为向量,
若,则,即.
故选:.
由已知结合向量平行的坐标表示即可求解.
本题主要考查了向量平行的坐标表示,属于基础题.
7.【答案】
【解析】解:,
,,
,
,
故选:.
根据三角函数的诱导公式进行转化,结合三角函数的单调性和取值范围进行比较即可.
本题主要考查三角函数值的大小比较,利用三角函数的诱导公式以及三角函数的单调性进行转化是解决本题的关键,是基础题.
8.【答案】
【解析】解:根据题意,,
其定义域为,有,则函数为奇函数,排除,
,排除.
故选:.
根据题意,先分析函数的奇偶性,排除,再计算的值,排除,综合可得答案.
本题考查函数的图象分析,涉及函数的奇偶性以及函数值符号的分析,属于基础题.
9.【答案】
【解析】解::根据三角函数线的概念,ABC正确;
:因为余弦线的始点在原点,而正切线的始点在单位圆与轴正半轴的交点上,故D错误.
故选:.
利用三角函数线的定义对各个选项逐个判断即可求解.
本题考查了三角函数线的应用,属于基础题.
10.【答案】
【解析】解:对于,,故A项错误;
对于,,故B正确;
对于,,故C正确;
对于,,故D错误.
故选:.
利用三角函数的诱导公式即可得解.
本题主要考查了诱导公式在三角函数求值中的应用,考查了转化思想,属于基础题.
11.【答案】
【解析】解:由函数的部分图象可得,
因为,,
所以,则,得.
所以,
将代入,得,
则,解得,
因为,
所以正确.
令,得错误.
,C错误,D正确.
故选:.
根据已知函数的部分图象可得,再结合函数的周期可得,然后将代入求得,即可求得函数的解析式,进而判断选项A的正误;利用三角函数的图象与性质求出函数的单调区间,即可判断选项B的正误;利用代入验证法判断函数的对称中心和对称轴即可判断选项C、的正误.
本题考查由的部分图象确定其解析式,考查运算求解能力,属于中档题.
12.【答案】
【解析】【分析】
本题考查扇形的面积、弧长公式,考查学生的计算能力,属于基础题.
利用扇形的圆心角为,弧长为,求出扇形的半径,再求扇形的面积.
【解答】
解:扇形的圆心角为,弧长为,
扇形的半径为,
扇形的面积为.
故答案为:.
13.【答案】
【解析】解:,
,
故答案为:.
由已知直接利用诱导公式化简求值.
本题考查三角函数的化简求值,考查诱导公式的应用,是基础题.
14.【答案】
【解析】解:依题意,
画出函数的图象,如图:
由图象知,当,即时,函数的图象与直线有且仅有两个不同的交点,
所以实数的取值范围是.
故答案为:.
将函数写成分段函数的形式,在同一坐标系下画出函数和函数图象,利用数形结合即可判断两函数有两个不同的交点时实数的取值范围.
本题考查三角函数的图象和性质,属于基础题.
15.【答案】解:
;
,,得,
则.
【解析】利用特殊角的三角函数值与三角函数的诱导公式即可得解;
先利用三角函数的诱导公式与基本关系式得到,再利用正余弦的齐次式法即可得解.
本题考查三角函数的化简求值,考查诱导公式及同角三角函数基本关系式的应用,是基础题.
16.【答案】解:由已知令,
则,
所以,
解得,
即当取得最大值时,的取值集合为;
当时,,
则,即
所以在上的值域为;
列表如下:
图象如下:
【解析】由已知可得,利用正弦函数的性质即可求解;
由题意可求,进而利用正弦函数的性质即可求解;
利用五点法完成表格,然后再作图即可.
本题考查了正弦函数的性质以及五点法作函数的图象,考查了函数思想,属于基础题.
17.【答案】解:由,得,
.
;
,,,则,
又,
;
由,可得.
.
【解析】两边平方,结合平方关系得由此即可进一步求解;
首先得,进一步由即可求解;
首先分别求得,,然后由商数关系即可求解.
本题考查三角函数的化简求值,考查同角三角函数的基本关系式的应用,是基础题.
18.【答案】解:如图,建立平面直角坐标系,
当时,风车开始旋转时某叶片的一个端点在风车的最低点,设为,则,
由题意得,,且,
解得,
所以;
令,则,
即,
所以,解得,
当时,,
所以叶片旋转一圈内点离地面的高度不低于米的时长为秒.
【解析】建立平面直角坐标系,根据题意列出方程组,求出,,的值,得到的解析式;
令,则,再结合正弦函数的性质求解.
本题主要考查了三角函数的应用,考查了正弦函数的图象和性质,属于中档题.
19.【答案】解:的最大值为,
,
又的图象过,
,
或,
,
,
;
由知,
由余弦函数的性质可得其增区间为,,
减区间为,;
,
令 ,,
则,,
当时,即,时,有最小值,
当时,即,时,有最大值.
【解析】根据函数的最值和过的点即可求得函数的解析式;
根据余弦函数的性质可得函数的单调区间;
换元后转化为二次函数,利用二次函数的性质求解即可.
本题考查了由的部分图象确定其解析式,余弦函数的性质以及二次函数的性质,考查了函数思想,属于中档题.
第1页,共1页
同课章节目录
