6.1感受可能性

(共19张PPT)
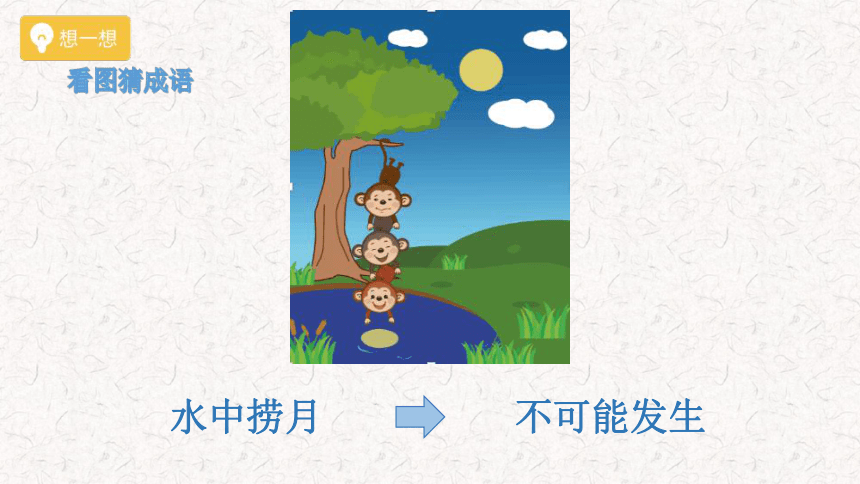
看图猜成语
水中捞月
不可能发生
看图猜成语
一箭双雕
可能发生
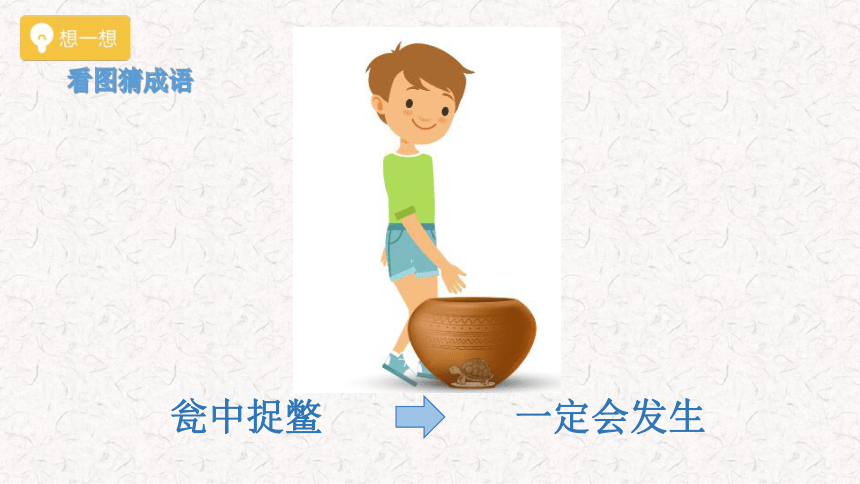
看图猜成语
瓮中捉鳖
一定会发生
感受可能性
第六章 概率初步
(1)随意掷一枚质地均匀的骰子，
掷出的点数会是10吗？
(2)随意掷一枚质地均匀的骰子，
掷出的点数一定不超过6吗？
(3)随意掷一枚质地均匀的骰子，
掷出的点数一定是1吗？
不可能
一定
不一定
在一定条件下，有些事件我们事先能肯定它一定发生，这些事情称为必然事件.
例如：随意掷一枚质地均匀的骰子，掷出的点数一定不超过6就是一个必然事件。
必然事件
在一定条件下，有些事情我们事先能肯定它一定不会发生，这些事情称为不可能事件.
例如:掷一枚质地均匀的骰子，掷出的点数是10就是 一个不可能事件.
不可能事件
有许多事情我们事先无法肯定它会不会发生，这些事情称为不确定事件，
也称为随机事件。
例如:掷一枚质地均匀的骰子，掷出的点数是1就是 一个随机事件.
随机事件
②明天，地球还会转动
③煮熟的鸭子，飞了
下列现象哪些是必然发生的，哪些是不可能发生的，哪些是不确定的？
①木柴燃烧,产生热量
必然
必然
不可能
只要功夫深，铁杵磨成针.
跳高运动员最终要落到地面上。
守株待兔
喜从天降
必然
必然
随机事件
随机事件
利用质地均匀的骰子和同桌做游戏，规则如下：
(1)两人同时做游戏，各自掷一枚骰子，每人可以只掷一次骰子，也可以连续地掷几次骰子.
(2)当掷出的点数和不超过10时，如果决定停止掷，那么你的得分就是所掷出的点数和；当掷出的点数和超过10时，必须停止掷，并且你的得分为0.
(3)比较两人的得分，谁的得分多谁就获胜.
多做几次上面的游戏，并将最终结果填入下表:
第1次点数 第2次点数 第3次点数 ··· 得分
第一次游戏 甲 ···
乙 ···
第二次游戏 甲 ···
乙 ···
第三次游戏 甲 ···
乙 ···
··· ··· ··· ··· ··· ··· ···
在做游戏的过程中，你是如何决定是继续掷骰子
还是停止掷骰子的？与同伴进行交流.
在做游戏的过程中，如果前面掷出的点数和已经是5，你是决定继续掷还是决定停止掷？如果掷出的点数和已经是9呢？
小明：掷出的点数和已经是5，根据游戏规则，再掷一次，如果掷出的点数不是6，那么我的得分就会增加，而掷出的点数不是6的可能性要比是6的可能性大，所以我决定继续掷.
小颖：掷出的点数和已经是9，再掷一次，如果掷出的点数不是1，那么我的得分就会变成0，而掷出的点数是1的可能性要比不是1的可能性小，所以我决定停止掷.
你认为小明和小颖的说法有道理吗？
一般地，不确定事件发生的可能性是有大有小的
例1.小明任意买一张电影票，座位号是2的倍数与座位号是5的倍数的可能性哪个大？
解：座位号是2的倍数的可能性大．
例2. 掷一枚普通的六面体骰子，有下列事件：
①掷得的点数是6；②掷得的点数是奇数；
③掷得的点数不大于4；④掷得的点数不小于2，
这些事件发生的可能性由大到小排列正确的是(　　)
A．①②③④　　 B．④③②①　　
C．③④②①　　 D．②③①④
B
一般地，事件包含的可能结果越多可能性就越大，反之，则越小
分析：①掷得的点数是6只有一种情况；
②掷得的点数是奇数包括3种情况；
③掷得的点数不大于4包括4种情况；
④掷得的点数不小于2包括5种情况，
故其可能性按从大到小的顺序排列为④③②①
例3. 桌上扣着背面图案相同的5张扑克牌，其中3张黑桃、2张红桃.从中随机抽取1张扑克牌.
（1）能够事先确定抽取的扑克牌的花色吗？
（2）你认为抽到哪种花色扑克牌的可能性大？
（3）能否通过改变某种花色的扑克牌的数量，使“抽到黑桃”和“抽到红桃”的可能性大小相同？
解：（1）不能确定；
（2）黑桃；
（3）可以，去掉一张黑桃或增加一张红桃.
小结
随机事件
事件
不可能事件
必然事件
确定事件
随机事件的特点：
1.事先不能预料事件是否发生，即事件的发生具有不确定性.
2.一般地，随机事件发生的可能性是有大小的.
作业布置
1.教材第138页习题6.1第1、2、3题；
2.请同学们小组探究139页问题解决，给出你的游戏策略。
谢 谢 观 看！