海南省琼海市嘉积中学2023-2024学年高一下学期阶段性教学检测(五)数学试题(含答案)
文档属性
| 名称 | 海南省琼海市嘉积中学2023-2024学年高一下学期阶段性教学检测(五)数学试题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 941.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 12:47:58 | ||
图片预览



文档简介
2023—2024学年海南高一年级阶段性教学检测(五)
数学
1.本试卷满分150分,测试时间120分钟,共4页.
2.考查范围:必修第二册整本书.
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若复数,则z在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在学校举办的教师优质课评比比赛中,八位评委打出八个完全不同的分数后,去掉一个最高分,去掉一个最低分,再用剩余的六个分数计算平均数,作为讲课教师的最后得分.那么剩余的六个分数与最初的八个分数相比较,一定不变的数字特征是
A.平均数 B.方差 C.极差 D.中位数
3.如图是某校高一年级1000名男生体检时身高的频率分布直方图,现用分层随机抽样的方法从身高在160~175cm的男生中抽取130名,则抽取到的身高在165~170cm的人数为
A.20 B.30 C.40 D.50
4.已知向量,,,若与垂直,则实数λ的值为
A. B. C. D.
5.已知α,β表示两个不同的平面,m为平面α内的一条直线,则“”是“”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.下表是某地区2024年3月1日至10日每天中午12时的气温统计表,则下列关于这10天中气温的说法错误的是
日期 1 2 3 4 5 6 7 8 9 10
气温(℃) 2 10 18 20 16 12 6 2 6 12
A.众数为2和6和12 B.70%分位数为16
C.平均数小于中位数 D.极差为18
7.在中,点D,N分别满足,,若,,则
A. B. C. D.
8.已知一个圆锥的顶点和底面的圆周在同一个球面上,若球的体积为36π,圆锥的体积为,且圆锥的高为正整数,则该圆锥的侧面积为
A. B. C. D.
二、选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.已知复数z满足,以下说法正确的是
A.复数z的虚部是 B.
C.在复平面内对应的点在第一象限 D.
10.某班有50名学生,某次数学考试的成绩经计算得到的平均分数为80分,标准差为s,后来发现记录有误,甲同学得90分误记为60分,乙同学得70分误记为100分,更正后重新计算得到的平均分数为,标准差为,则下列说法正确的是
A. B. C. D.
11.如图,在正四棱柱中,,点P为线段上的动点,则下列说法正确的是
A.三棱锥的体积为
B.三棱锥外接球的表面积为6π
C.若E是棱上一点,且,则平面
D.直线平面
三、填空题(本题共3小题,每小题5分,共15分)
12.数据:7.2,8.3,8.5,8.5,8.7,8.8,9.0,9.2的第40百分位数是________.
13.已知向量、的夹角为,,,则向量在向量上的投影向量为________.
14.已知中,,,且的面积为,若直线AB上存在点D,使,则________.
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)已知向量,.
(Ⅰ)求;
(Ⅱ)已知,且,求向量与向量的夹角.
16.(15分)某校组织全校数学老师参加解题大赛,对于大赛中的最后一个解答题,甲得满分的概率为0.8,乙得满分的概率为0.7,记事件A:甲最后一个解答题得满分,事件B:乙最后一个解答题得满分.
(Ⅰ)求甲、乙两人最后一个解答题都得满分的概率;
(Ⅱ)求甲、乙恰有一人最后一个解答题得满分的概率.
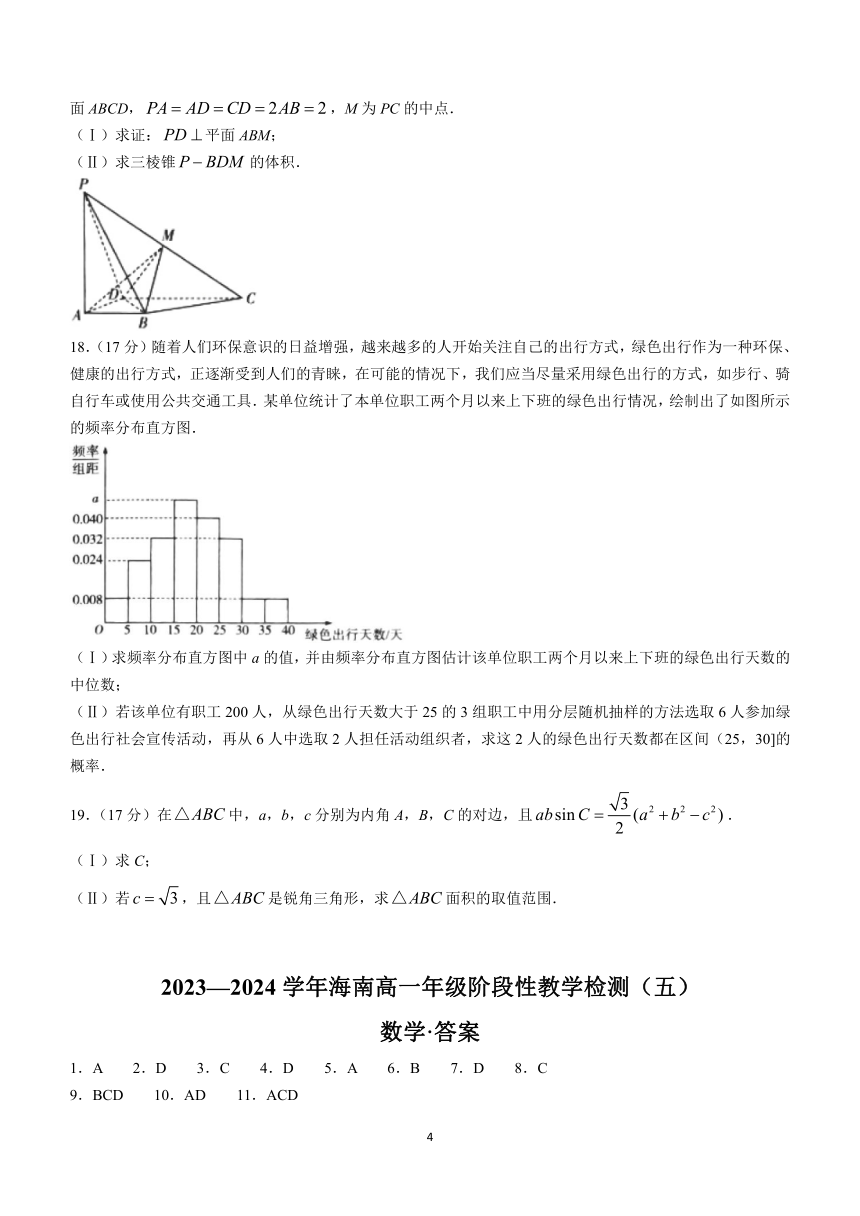
17.(15分)如图,在四棱锥中,底面ABCD是梯形,其中,且,平面ABCD,,M为PC的中点.
(Ⅰ)求证:平面ABM;
(Ⅱ)求三棱锥的体积.
18.(17分)随着人们环保意识的日益增强,越来越多的人开始关注自己的出行方式,绿色出行作为一种环保、健康的出行方式,正逐渐受到人们的青睐,在可能的情况下,我们应当尽量采用绿色出行的方式,如步行、骑自行车或使用公共交通工具.某单位统计了本单位职工两个月以来上下班的绿色出行情况,绘制出了如图所示的频率分布直方图.
(Ⅰ)求频率分布直方图中a的值,并由频率分布直方图估计该单位职工两个月以来上下班的绿色出行天数的中位数;
(Ⅱ)若该单位有职工200人,从绿色出行天数大于25的3组职工中用分层随机抽样的方法选取6人参加绿色出行社会宣传活动,再从6人中选取2人担任活动组织者,求这2人的绿色出行天数都在区间(25,30]的概率.
19.(17分)在中,a,b,c分别为内角A,B,C的对边,且.
(Ⅰ)求C;
(Ⅱ)若,且是锐角三角形,求面积的取值范围.
2023—2024学年海南高一年级阶段性教学检测(五)
数学·答案
1.A 2.D 3.C 4.D 5.A 6.B 7.D 8.C
9.BCD 10.AD 11.ACD
12.8.5 13. 14.2或
15.解:(Ⅰ)由向量,,得,
所以.
(Ⅱ)由,,
得,
解得,
由,得,
所以,
又,所以,
所以向量与向量的夹角为.
16.解:(Ⅰ)事件“甲、乙两人最后一个解答题都得满分”可表示为AB,且事件A,B相互独立,
由题意可知,,
所以.
(Ⅱ)因为事件“甲、乙恰有一人最后一个解答题得满分”可表示为,且,互斥,
所以
.
17.解:(Ⅰ)如图,取PD的中点E,连接EM,AE,则且.
∵且,
∴,即A,B,M,E四点共面.
∵平面ABCD,平面ABCD,
∴,又,,
∴平面PAD,
∵平面PAD,
∴.
又,E是PD的中点,
∴,又,
∴平面ABME,即平面ABM.
(Ⅱ)∵,平面PDM,平面PDM,
∴平面PDM,即点B到平面PDM的距离等于线段AB到平面PDM的距离.
∵,,PD,平面PDM,,
∴平面PDM,
∴
.
18.解:(Ⅰ)由题意得,解得.
由,,
知中位数位于(15,20]内.
设中位数为,
则,解得,
则中位数为.
(Ⅱ)绿色出行天数大于25的共有(人),
则在区间(25,30]中的有(人),抽取人数为,
在区间(30,35]中的有(人),抽取人数为,
在区间(35,40]中的有(人),抽取人数为.
设从绿色出行天数在(25,30]中抽取的职工为,,,,从绿色出行天数在(30,35]中抽取的职工为B,从绿色出行天数在(35,40]中抽取的职工为C,全部可能的结果有(,),(,),(,),(,B),(,C),(,),(,),(,B),(,C),(,),(,B),(,C),(,B),(,C),(B,C),
样本点总数,
满足要求的样本点个数,
则两人均来自(25,30]的概率为
,
故2人的绿色出行天数都在区间(25,30]的概率为.
19.解:(Ⅰ)由,且,
得,即,
又,
所以.
(Ⅱ)由正弦定理可得,
,
所以,,
所以的面积
.
由是锐角三角形,得
即,
所以,
所以,
所以,
所以面积的取值范围为.
数学
1.本试卷满分150分,测试时间120分钟,共4页.
2.考查范围:必修第二册整本书.
一、选择题(本题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若复数,则z在复平面内对应的点位于
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.在学校举办的教师优质课评比比赛中,八位评委打出八个完全不同的分数后,去掉一个最高分,去掉一个最低分,再用剩余的六个分数计算平均数,作为讲课教师的最后得分.那么剩余的六个分数与最初的八个分数相比较,一定不变的数字特征是
A.平均数 B.方差 C.极差 D.中位数
3.如图是某校高一年级1000名男生体检时身高的频率分布直方图,现用分层随机抽样的方法从身高在160~175cm的男生中抽取130名,则抽取到的身高在165~170cm的人数为
A.20 B.30 C.40 D.50
4.已知向量,,,若与垂直,则实数λ的值为
A. B. C. D.
5.已知α,β表示两个不同的平面,m为平面α内的一条直线,则“”是“”的
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分也不必要条件
6.下表是某地区2024年3月1日至10日每天中午12时的气温统计表,则下列关于这10天中气温的说法错误的是
日期 1 2 3 4 5 6 7 8 9 10
气温(℃) 2 10 18 20 16 12 6 2 6 12
A.众数为2和6和12 B.70%分位数为16
C.平均数小于中位数 D.极差为18
7.在中,点D,N分别满足,,若,,则
A. B. C. D.
8.已知一个圆锥的顶点和底面的圆周在同一个球面上,若球的体积为36π,圆锥的体积为,且圆锥的高为正整数,则该圆锥的侧面积为
A. B. C. D.
二、选择题(本题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分)
9.已知复数z满足,以下说法正确的是
A.复数z的虚部是 B.
C.在复平面内对应的点在第一象限 D.
10.某班有50名学生,某次数学考试的成绩经计算得到的平均分数为80分,标准差为s,后来发现记录有误,甲同学得90分误记为60分,乙同学得70分误记为100分,更正后重新计算得到的平均分数为,标准差为,则下列说法正确的是
A. B. C. D.
11.如图,在正四棱柱中,,点P为线段上的动点,则下列说法正确的是
A.三棱锥的体积为
B.三棱锥外接球的表面积为6π
C.若E是棱上一点,且,则平面
D.直线平面
三、填空题(本题共3小题,每小题5分,共15分)
12.数据:7.2,8.3,8.5,8.5,8.7,8.8,9.0,9.2的第40百分位数是________.
13.已知向量、的夹角为,,,则向量在向量上的投影向量为________.
14.已知中,,,且的面积为,若直线AB上存在点D,使,则________.
四、解答题(本题共5小题,共77分.解答应写出文字说明、证明过程或演算步骤)
15.(13分)已知向量,.
(Ⅰ)求;
(Ⅱ)已知,且,求向量与向量的夹角.
16.(15分)某校组织全校数学老师参加解题大赛,对于大赛中的最后一个解答题,甲得满分的概率为0.8,乙得满分的概率为0.7,记事件A:甲最后一个解答题得满分,事件B:乙最后一个解答题得满分.
(Ⅰ)求甲、乙两人最后一个解答题都得满分的概率;
(Ⅱ)求甲、乙恰有一人最后一个解答题得满分的概率.
17.(15分)如图,在四棱锥中,底面ABCD是梯形,其中,且,平面ABCD,,M为PC的中点.
(Ⅰ)求证:平面ABM;
(Ⅱ)求三棱锥的体积.
18.(17分)随着人们环保意识的日益增强,越来越多的人开始关注自己的出行方式,绿色出行作为一种环保、健康的出行方式,正逐渐受到人们的青睐,在可能的情况下,我们应当尽量采用绿色出行的方式,如步行、骑自行车或使用公共交通工具.某单位统计了本单位职工两个月以来上下班的绿色出行情况,绘制出了如图所示的频率分布直方图.
(Ⅰ)求频率分布直方图中a的值,并由频率分布直方图估计该单位职工两个月以来上下班的绿色出行天数的中位数;
(Ⅱ)若该单位有职工200人,从绿色出行天数大于25的3组职工中用分层随机抽样的方法选取6人参加绿色出行社会宣传活动,再从6人中选取2人担任活动组织者,求这2人的绿色出行天数都在区间(25,30]的概率.
19.(17分)在中,a,b,c分别为内角A,B,C的对边,且.
(Ⅰ)求C;
(Ⅱ)若,且是锐角三角形,求面积的取值范围.
2023—2024学年海南高一年级阶段性教学检测(五)
数学·答案
1.A 2.D 3.C 4.D 5.A 6.B 7.D 8.C
9.BCD 10.AD 11.ACD
12.8.5 13. 14.2或
15.解:(Ⅰ)由向量,,得,
所以.
(Ⅱ)由,,
得,
解得,
由,得,
所以,
又,所以,
所以向量与向量的夹角为.
16.解:(Ⅰ)事件“甲、乙两人最后一个解答题都得满分”可表示为AB,且事件A,B相互独立,
由题意可知,,
所以.
(Ⅱ)因为事件“甲、乙恰有一人最后一个解答题得满分”可表示为,且,互斥,
所以
.
17.解:(Ⅰ)如图,取PD的中点E,连接EM,AE,则且.
∵且,
∴,即A,B,M,E四点共面.
∵平面ABCD,平面ABCD,
∴,又,,
∴平面PAD,
∵平面PAD,
∴.
又,E是PD的中点,
∴,又,
∴平面ABME,即平面ABM.
(Ⅱ)∵,平面PDM,平面PDM,
∴平面PDM,即点B到平面PDM的距离等于线段AB到平面PDM的距离.
∵,,PD,平面PDM,,
∴平面PDM,
∴
.
18.解:(Ⅰ)由题意得,解得.
由,,
知中位数位于(15,20]内.
设中位数为,
则,解得,
则中位数为.
(Ⅱ)绿色出行天数大于25的共有(人),
则在区间(25,30]中的有(人),抽取人数为,
在区间(30,35]中的有(人),抽取人数为,
在区间(35,40]中的有(人),抽取人数为.
设从绿色出行天数在(25,30]中抽取的职工为,,,,从绿色出行天数在(30,35]中抽取的职工为B,从绿色出行天数在(35,40]中抽取的职工为C,全部可能的结果有(,),(,),(,),(,B),(,C),(,),(,),(,B),(,C),(,),(,B),(,C),(,B),(,C),(B,C),
样本点总数,
满足要求的样本点个数,
则两人均来自(25,30]的概率为
,
故2人的绿色出行天数都在区间(25,30]的概率为.
19.解:(Ⅰ)由,且,
得,即,
又,
所以.
(Ⅱ)由正弦定理可得,
,
所以,,
所以的面积
.
由是锐角三角形,得
即,
所以,
所以,
所以,
所以面积的取值范围为.
同课章节目录
