吉林省部分名校2023-2024学年高一下学期联合考试数学试题(含解析)
文档属性
| 名称 | 吉林省部分名校2023-2024学年高一下学期联合考试数学试题(含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 12:51:10 | ||
图片预览




文档简介
高一数学试卷
注意事项:
1.答题前,考生务必将自已的姓名 考生号 考场号 座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.本试卷主要考试内容:人教A版必修第二册第六章至第九章.
一 选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数的虚部为( )
A.1 B. C.3 D.
2.某纺织厂4月份生产了三种类型的纱线,分别为大卷纱线 中卷纱线和小卷纱线,其中大卷纱线有2000卷,中卷纱线有8000卷,小卷纱线有20000卷.为检查该纺织厂4月份生产的这三种类型纱线的质量,按比例用分层随机抽样的方法从中抽检240卷,则被抽检的小卷纱线有( )
A.120卷 B.150卷 C.160卷 D.200卷
3.有一艘船以每小时25海里的速度向正东方向行驶,在处测得灯塔在该船的东北方向,该船行驶2小时后到达处,测得灯塔在该船的东偏北方向上,则( )
A.海里 B.海里 C.50海里 D.海里
4.小唐5月日每天的运动时长(单位:分钟)统计数据如图所示,则( )
A.小唐这7天每天运动时长的平均数是72
B.小唐这7天每天运动时长的极差题42
C.小唐这7天每天运动时长的中位数是75
D.小唐这7天每天运动时长的第80百分位数是92
5.若某圆台的上底面半径为1,下底面半径为4,该圆台的体积不小于,则该圆台的高的取值范围是( )
A. B. C. D.
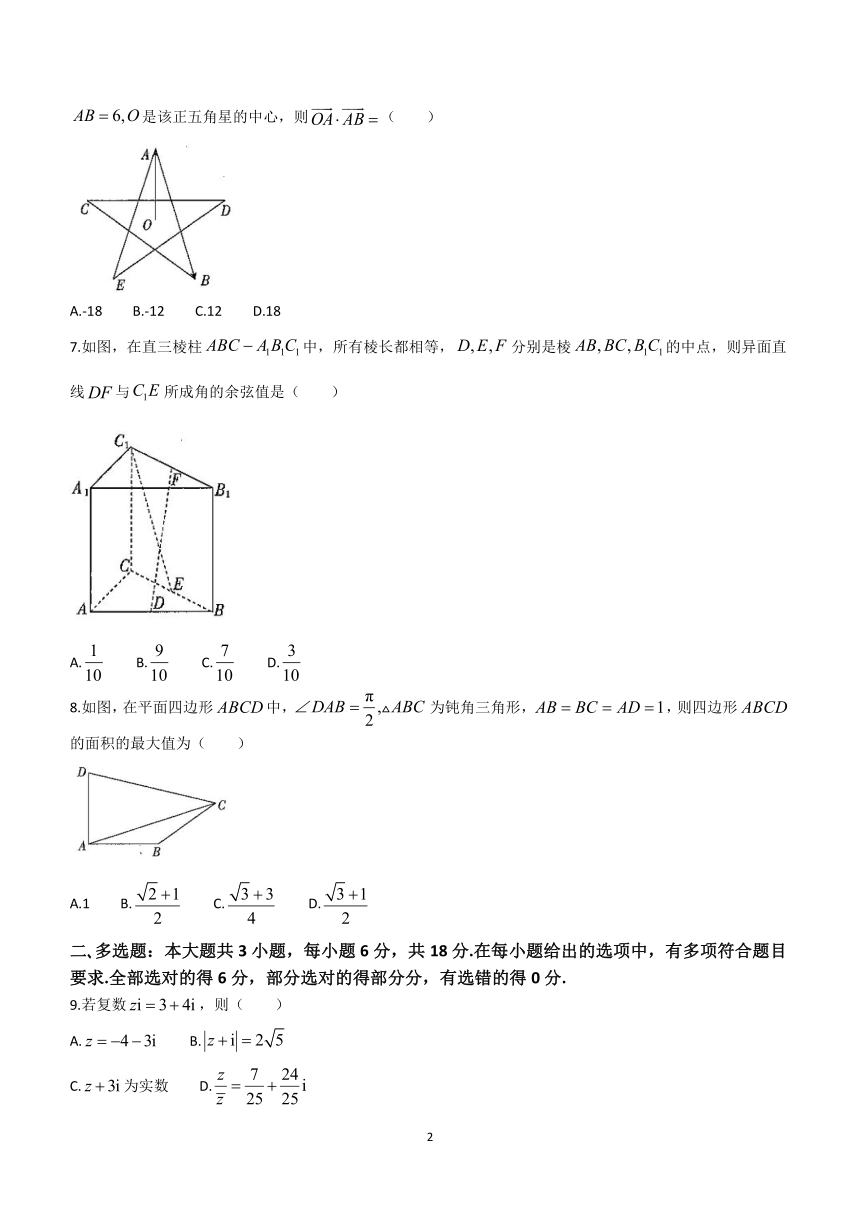
6.正五角星是一个非常优美的几何图形,且与黄金分割有着密切的联系.在如图所示的正五角星中,是该正五角星的中心,则( )
A.-18 B.-12 C.12 D.18
7.如图,在直三棱柱中,所有棱长都相等,分别是棱的中点,则异面直线与所成角的余弦值是( )
A. B. C. D.
8.如图,在平面四边形中,为钝角三角形,,则四边形的面积的最大值为( )
A.1 B. C. D.
二 多选题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.若复数,则( )
A. B.
C.为实数 D.
10.在正三棱锥中,,则下列结论正确的是( )
A.若,则二面角是
B.若二面角是,则正三棱锥的体积是
C.荅,则正三棱锥内切球的半径是.
D.若,则正三梭锥外接球的表面积为
11.欧拉线定理指出三角形的外心 垂心 重心都在同一条直线士,且重心与外心之间的距离是重心与垂心之间的距离的一半.设分别是的外心 垂心和重心,则( )
A. B.
C. D.
三 填空题:本大题共3小题,每小题5分,共15分.把答案填在答题卡中的横线上.
12.已知复数在复平面内对应的点分别为,若,则实数__________;若,则实数__________.
13.某校高一(1)班有男生20人,女生30人.已知某次数学测验中,男生成绩的平均数为100,方差为11,女生成绩的平均数为95,方差为16,则这次测验中班级总体成绩的方差为__________.
14.在棱长为4的正方体中,分别为线段上的动点,点为侧面的中心,则的周长的最小值为__________.
四 解答题:本大题共5小题,共77分.解答应写出文字说明 证明过程或演算步骤.
15.(13分)
如图,在直四梭柱中,底面为菱形,为的中点.
(1)证明:平面.
(2)求点到平面的距离.
16.(15分)
在中,角的对边分别是,已知,且.
(1)求角的大小;
(2)若,求面积的最大值.
17.(15分)
近年来,由于互联网的普及,直播带货已经成为推动消费的一种营销形式.某直播平台工作人员在问询了解了本平台600个直播商家的利润状况后,随机抽取了100个商家的取均日利润(单位:百元)进行统计,所得的频率分布直方图如图所示.
(1)求的值,并估计该直播平台商家平均日利润的平均数(同一组中的数据用该组区间的中点值作代表)与中位数.
(2)以样本估计总体,该直播平台为了鼓励直播带货,提出了两种奖淤方案,方案一是对平均日利润超过78百元的商家进行奖励,方案二是对平均日利润从高到低排名在前的商家进行奖励,两种奖励方案只选择一种,你觉得哪种方案受到奖励的商家更多?并说明理由.
18.(17分)
对任意两个非零向量,定义:.
(1)若向量,求的值;
(2)若单位向量满足,求向量与的夹角的余弦值;
(3)若非零向量满足,向量与的夹角是锐角,且是整数,求的取值范围.
19.(17分)
如图,在四棱锥中,在线段上(不含端点),底面.
(1)证明:平面平面.
(2)设,请写出三棱锥的体积关于的函数表达式,并求出的最大值.
高一数学试卷参考答案
1.A 因为,所以的虚部为1.
2.C 依题意得被抽检的小卷纱线有卷.
3.A 由题可知海里.在中,由正弦定理可得,则海里.
4.D ,A错误.小唐这7天每天运动时长的极差是,B错误.将小唐这7天每天运动时长从小到大排列为,则小唐这7天每天运动时长的中位数是70,错误.因为,所以第80百分位数是第6个数,即92,D正确.
5.B 设该圆台的高为,则该圆台的体积.因为该圆台的体积不小于,所以,解得.
6.A 由题意可得.
7.B 如图,取棱的中点,连接,易证四边形是平行四边形,则,故是异面直线与所成的角或补角.设,则.在中,由余弦定理可得.
8.B (方法一)设,则,因为,所以.四边形的面积为.,当,即时,四边形的面积取得最大值,最大值为.
(方法二)四边形的面积.
9.BC 由,得,A错误.,B正确.因为
,所以为实数,C正确.D错误.
10.ABD 如图,取的中点,连接,则是二面角的平面角.作平面,垂足为,易证在上,且.对于A,由,得,则,从而,故A正确.对于B,二面角是,即,得,则3,从而三棱锥的体积,故B正确.由,得.对于,设三棱锥内切球的半径为,则,所以,故C错误.设三棱锥外接球的半径为,球心为,且在上,连接,则,即,解得,所以,所以,故D正确.
11.BCD 连接并延长,交于点(图略),则是的中点.因为是的中点,所以,所以.当时,不共线,则,故A错误.由欧拉线定理可知,则,从而,故B正确.因为是的垂心,所以,所以,所以,则,故C正确.由欧拉线定理可知,则,即,故D正确.
12.; 依题意得,则.若,则,解得;若,则,解得.
13.20 依题意得这次测验中班级总体成绩的平均数为,方差为.
14. 如图①,设侧面的中心为,根据正方体的结构特征可得,则周长的最小值即的最小值.
将侧面绕着旋转至与平面在同一平面上,将平面绕着旋转至与平面在同一平面上,如图②,则
,故的周长的最小值为.
15.(1)证明:连接,设与交于点,易得为的中点,连接.
因为为的中点,所以为的中位线,则,
因为平面平面,所以平面.
(2)解:延长交于点,连接,取的中点,连接,
易得.
由题意易得为等边三角形,所以.因为平面,所以,所以平面,则点到平面的距离为.
.
因为,所以.
设点到平面的距离为,则.
由,得,解得.
故点到平面的距离为.
16.解:(1)因为,所以.
因为,所以,
所以,解得或.
因为,所以,则.
(2)因为,所以,即,则.
因为,所以.
因为,当且仅当时,等号成立,
所以,即,
则的面积,故面积的最大值为.
17.解:(1)由题意可知,解得.
由,解得,所以中位数约为74,
平均数约为.
(2)由题意可知,方案一受到奖励的商家的个数为,
方案二受到奖励的商家的个数为,
因为,所以方案一受到奖励的商家更多.
18.解:(1)因为,所以,
则,
故.
(2)因为,所以,所以,
所以,解得.
因为,所以,
则.
(3)设向量与的夹角为,由题意可知,则.
因为,所以,所以.
因为,所以,所以.
因为是整数,所以,所以,
所以.
因为,所以,所以,所以,所以,
所以,即的取值范围是.
19.(1)证明:因为底面底面,所以.
又因为,所以平面.
因为平面,所以平面平面.
(2)解:过点作,交于,连接.
由,得,因为
,所以,则,所以,
则,
.
因为底面,所以,所以平面,
所以.
因为,所以,
则,
所以.
因为,所以
所以当时,取得最大值,最大值为.
注意事项:
1.答题前,考生务必将自已的姓名 考生号 考场号 座位号填写在答题卡上.
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑.如需改动,用橡皮擦干净后,再选涂其他答案标号.回答非选择题时,将答案写在答题卡上.写在本试卷上无效.
3.考试结束后,将本试卷和答题卡一并交回.
4.本试卷主要考试内容:人教A版必修第二册第六章至第九章.
一 选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.复数的虚部为( )
A.1 B. C.3 D.
2.某纺织厂4月份生产了三种类型的纱线,分别为大卷纱线 中卷纱线和小卷纱线,其中大卷纱线有2000卷,中卷纱线有8000卷,小卷纱线有20000卷.为检查该纺织厂4月份生产的这三种类型纱线的质量,按比例用分层随机抽样的方法从中抽检240卷,则被抽检的小卷纱线有( )
A.120卷 B.150卷 C.160卷 D.200卷
3.有一艘船以每小时25海里的速度向正东方向行驶,在处测得灯塔在该船的东北方向,该船行驶2小时后到达处,测得灯塔在该船的东偏北方向上,则( )
A.海里 B.海里 C.50海里 D.海里
4.小唐5月日每天的运动时长(单位:分钟)统计数据如图所示,则( )
A.小唐这7天每天运动时长的平均数是72
B.小唐这7天每天运动时长的极差题42
C.小唐这7天每天运动时长的中位数是75
D.小唐这7天每天运动时长的第80百分位数是92
5.若某圆台的上底面半径为1,下底面半径为4,该圆台的体积不小于,则该圆台的高的取值范围是( )
A. B. C. D.
6.正五角星是一个非常优美的几何图形,且与黄金分割有着密切的联系.在如图所示的正五角星中,是该正五角星的中心,则( )
A.-18 B.-12 C.12 D.18
7.如图,在直三棱柱中,所有棱长都相等,分别是棱的中点,则异面直线与所成角的余弦值是( )
A. B. C. D.
8.如图,在平面四边形中,为钝角三角形,,则四边形的面积的最大值为( )
A.1 B. C. D.
二 多选题:本大题共3小题,每小题6分,共18分.在每小题给出的选项中,有多项符合题目要求.全部选对的得6分,部分选对的得部分分,有选错的得0分.
9.若复数,则( )
A. B.
C.为实数 D.
10.在正三棱锥中,,则下列结论正确的是( )
A.若,则二面角是
B.若二面角是,则正三棱锥的体积是
C.荅,则正三棱锥内切球的半径是.
D.若,则正三梭锥外接球的表面积为
11.欧拉线定理指出三角形的外心 垂心 重心都在同一条直线士,且重心与外心之间的距离是重心与垂心之间的距离的一半.设分别是的外心 垂心和重心,则( )
A. B.
C. D.
三 填空题:本大题共3小题,每小题5分,共15分.把答案填在答题卡中的横线上.
12.已知复数在复平面内对应的点分别为,若,则实数__________;若,则实数__________.
13.某校高一(1)班有男生20人,女生30人.已知某次数学测验中,男生成绩的平均数为100,方差为11,女生成绩的平均数为95,方差为16,则这次测验中班级总体成绩的方差为__________.
14.在棱长为4的正方体中,分别为线段上的动点,点为侧面的中心,则的周长的最小值为__________.
四 解答题:本大题共5小题,共77分.解答应写出文字说明 证明过程或演算步骤.
15.(13分)
如图,在直四梭柱中,底面为菱形,为的中点.
(1)证明:平面.
(2)求点到平面的距离.
16.(15分)
在中,角的对边分别是,已知,且.
(1)求角的大小;
(2)若,求面积的最大值.
17.(15分)
近年来,由于互联网的普及,直播带货已经成为推动消费的一种营销形式.某直播平台工作人员在问询了解了本平台600个直播商家的利润状况后,随机抽取了100个商家的取均日利润(单位:百元)进行统计,所得的频率分布直方图如图所示.
(1)求的值,并估计该直播平台商家平均日利润的平均数(同一组中的数据用该组区间的中点值作代表)与中位数.
(2)以样本估计总体,该直播平台为了鼓励直播带货,提出了两种奖淤方案,方案一是对平均日利润超过78百元的商家进行奖励,方案二是对平均日利润从高到低排名在前的商家进行奖励,两种奖励方案只选择一种,你觉得哪种方案受到奖励的商家更多?并说明理由.
18.(17分)
对任意两个非零向量,定义:.
(1)若向量,求的值;
(2)若单位向量满足,求向量与的夹角的余弦值;
(3)若非零向量满足,向量与的夹角是锐角,且是整数,求的取值范围.
19.(17分)
如图,在四棱锥中,在线段上(不含端点),底面.
(1)证明:平面平面.
(2)设,请写出三棱锥的体积关于的函数表达式,并求出的最大值.
高一数学试卷参考答案
1.A 因为,所以的虚部为1.
2.C 依题意得被抽检的小卷纱线有卷.
3.A 由题可知海里.在中,由正弦定理可得,则海里.
4.D ,A错误.小唐这7天每天运动时长的极差是,B错误.将小唐这7天每天运动时长从小到大排列为,则小唐这7天每天运动时长的中位数是70,错误.因为,所以第80百分位数是第6个数,即92,D正确.
5.B 设该圆台的高为,则该圆台的体积.因为该圆台的体积不小于,所以,解得.
6.A 由题意可得.
7.B 如图,取棱的中点,连接,易证四边形是平行四边形,则,故是异面直线与所成的角或补角.设,则.在中,由余弦定理可得.
8.B (方法一)设,则,因为,所以.四边形的面积为.,当,即时,四边形的面积取得最大值,最大值为.
(方法二)四边形的面积.
9.BC 由,得,A错误.,B正确.因为
,所以为实数,C正确.D错误.
10.ABD 如图,取的中点,连接,则是二面角的平面角.作平面,垂足为,易证在上,且.对于A,由,得,则,从而,故A正确.对于B,二面角是,即,得,则3,从而三棱锥的体积,故B正确.由,得.对于,设三棱锥内切球的半径为,则,所以,故C错误.设三棱锥外接球的半径为,球心为,且在上,连接,则,即,解得,所以,所以,故D正确.
11.BCD 连接并延长,交于点(图略),则是的中点.因为是的中点,所以,所以.当时,不共线,则,故A错误.由欧拉线定理可知,则,从而,故B正确.因为是的垂心,所以,所以,所以,则,故C正确.由欧拉线定理可知,则,即,故D正确.
12.; 依题意得,则.若,则,解得;若,则,解得.
13.20 依题意得这次测验中班级总体成绩的平均数为,方差为.
14. 如图①,设侧面的中心为,根据正方体的结构特征可得,则周长的最小值即的最小值.
将侧面绕着旋转至与平面在同一平面上,将平面绕着旋转至与平面在同一平面上,如图②,则
,故的周长的最小值为.
15.(1)证明:连接,设与交于点,易得为的中点,连接.
因为为的中点,所以为的中位线,则,
因为平面平面,所以平面.
(2)解:延长交于点,连接,取的中点,连接,
易得.
由题意易得为等边三角形,所以.因为平面,所以,所以平面,则点到平面的距离为.
.
因为,所以.
设点到平面的距离为,则.
由,得,解得.
故点到平面的距离为.
16.解:(1)因为,所以.
因为,所以,
所以,解得或.
因为,所以,则.
(2)因为,所以,即,则.
因为,所以.
因为,当且仅当时,等号成立,
所以,即,
则的面积,故面积的最大值为.
17.解:(1)由题意可知,解得.
由,解得,所以中位数约为74,
平均数约为.
(2)由题意可知,方案一受到奖励的商家的个数为,
方案二受到奖励的商家的个数为,
因为,所以方案一受到奖励的商家更多.
18.解:(1)因为,所以,
则,
故.
(2)因为,所以,所以,
所以,解得.
因为,所以,
则.
(3)设向量与的夹角为,由题意可知,则.
因为,所以,所以.
因为,所以,所以.
因为是整数,所以,所以,
所以.
因为,所以,所以,所以,所以,
所以,即的取值范围是.
19.(1)证明:因为底面底面,所以.
又因为,所以平面.
因为平面,所以平面平面.
(2)解:过点作,交于,连接.
由,得,因为
,所以,则,所以,
则,
.
因为底面,所以,所以平面,
所以.
因为,所以,
则,
所以.
因为,所以
所以当时,取得最大值,最大值为.
同课章节目录
