初中数学人教版七年级下册6.3实数 作业设计(无答案)
文档属性
| 名称 | 初中数学人教版七年级下册6.3实数 作业设计(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 87.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 16:49:09 | ||
图片预览

文档简介
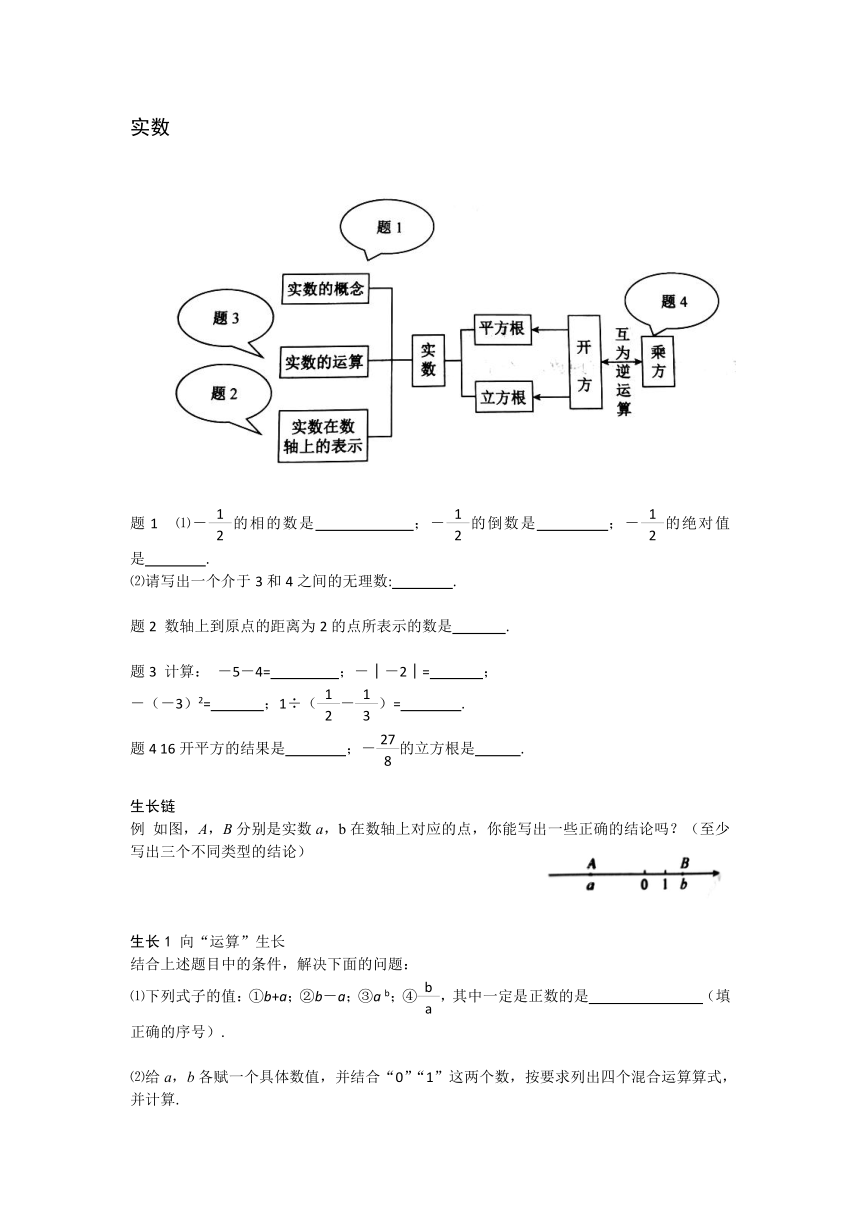
实数
题1 ⑴-的相的数是 ;-的倒数是 ;-的绝对值是 .
⑵请写出一个介于3和4之间的无理数: .
题2 数轴上到原点的距离为2的点所表示的数是 .
题3 计算: -5-4= ;-│-2│= ;
-(-3)2= ;1÷(-)= .
题4 16开平方的结果是 ;-的立方根是 .
生长链
例 如图,A,B分别是实数a,b在数轴上对应的点,你能写出一些正确的结论吗?(至少写出三个不同类型的结论)
生长1 向“运算”生长
结合上述题目中的条件,解决下面的问题:
⑴下列式子的值:①b+a;②b-a;③a b;④,其中一定是正数的是 (填正确的序号).
⑵给a,b各赋一个具体数值,并结合“0”“1”这两个数,按要求列出四个混合运算算式,并计算.
①a= ,,b= ,算式为 .
(要求:a,b都是有理数,只含加减两种运算)
②a= ,b= ,算式为 .
(要求:a,b中一个是有理数,一个是无理数,至少有三种运算)
③a= ,b= ,算式为 .
(要求:a,b中都是无理数,至少有四种运算)
生长2 向“不等关系”生长
结合例题中的条件,比较下列实数的大小,并用“>”连接:a,│a│,b,-b.
生长2 向“形”生长
在数轴上用直尺和圆规画出对应的点.
贯通路
1. 我们把求若干个相同的不为零的有理数的除法运算叫做除方,将(a≠0)记作a,读作“a的圈n次方” .
⑴直接写出计算结果:2③= ,(-)⑤= .
⑵关于除方,下列说法错误的是 ( )
A.任何非零数的圈2次方都等于1
B.对于任何正整数n,1=1
C.3④=4③
D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
生长 向“关系”生长
说说除方运算与乘方运算性质的区别和联系,并尝试用符号表示.
2. 我们知道,│7-3│表示7与3的差的绝对值,也可理解为7与3两数在数轴上所对应的两点之间的距离;│7+3│可以看作│7-(-3)│,表示7与-3的差的绝对值,也可理解为7与-3两数在数轴上所对应的两点之间的距离.
⑴计算:│5-(-2)│= .
⑵利用数轴,写出所有符合的整数x,使x所表示的点到5和-2对应点的距离之和为7.
⑶根据以上的探索思考,对于任何有理数x,式子│x-3│+│x+6│是否有最小值?如果有,直接写出最小值;如果没有,请说明理由.
生长 向“一般化”生长
解关于x的方程,│x-3│+│x+6│=a(a为常数).
题1 ⑴-的相的数是 ;-的倒数是 ;-的绝对值是 .
⑵请写出一个介于3和4之间的无理数: .
题2 数轴上到原点的距离为2的点所表示的数是 .
题3 计算: -5-4= ;-│-2│= ;
-(-3)2= ;1÷(-)= .
题4 16开平方的结果是 ;-的立方根是 .
生长链
例 如图,A,B分别是实数a,b在数轴上对应的点,你能写出一些正确的结论吗?(至少写出三个不同类型的结论)
生长1 向“运算”生长
结合上述题目中的条件,解决下面的问题:
⑴下列式子的值:①b+a;②b-a;③a b;④,其中一定是正数的是 (填正确的序号).
⑵给a,b各赋一个具体数值,并结合“0”“1”这两个数,按要求列出四个混合运算算式,并计算.
①a= ,,b= ,算式为 .
(要求:a,b都是有理数,只含加减两种运算)
②a= ,b= ,算式为 .
(要求:a,b中一个是有理数,一个是无理数,至少有三种运算)
③a= ,b= ,算式为 .
(要求:a,b中都是无理数,至少有四种运算)
生长2 向“不等关系”生长
结合例题中的条件,比较下列实数的大小,并用“>”连接:a,│a│,b,-b.
生长2 向“形”生长
在数轴上用直尺和圆规画出对应的点.
贯通路
1. 我们把求若干个相同的不为零的有理数的除法运算叫做除方,将(a≠0)记作a,读作“a的圈n次方” .
⑴直接写出计算结果:2③= ,(-)⑤= .
⑵关于除方,下列说法错误的是 ( )
A.任何非零数的圈2次方都等于1
B.对于任何正整数n,1=1
C.3④=4③
D.负数的圈奇数次方结果是负数,负数的圈偶数次方结果是正数
生长 向“关系”生长
说说除方运算与乘方运算性质的区别和联系,并尝试用符号表示.
2. 我们知道,│7-3│表示7与3的差的绝对值,也可理解为7与3两数在数轴上所对应的两点之间的距离;│7+3│可以看作│7-(-3)│,表示7与-3的差的绝对值,也可理解为7与-3两数在数轴上所对应的两点之间的距离.
⑴计算:│5-(-2)│= .
⑵利用数轴,写出所有符合的整数x,使x所表示的点到5和-2对应点的距离之和为7.
⑶根据以上的探索思考,对于任何有理数x,式子│x-3│+│x+6│是否有最小值?如果有,直接写出最小值;如果没有,请说明理由.
生长 向“一般化”生长
解关于x的方程,│x-3│+│x+6│=a(a为常数).
