沪科版八年级数学下册试题 第十七章 一元二次方程 章节测试卷(含解析)
文档属性
| 名称 | 沪科版八年级数学下册试题 第十七章 一元二次方程 章节测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 310.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 00:00:00 | ||
图片预览




文档简介
第十七章《一元二次方程》章节测试卷
一.选择题(共10小题,满分30分,每小题3分)
1.下列一元二次方程中,有两个相等的实数根的是( )
A. B.
C. D.
2.关于的一元二次方程的解为,,则代数式的值为( )
A.1 B.0 C. D.
3.已知关于的一元二次方程有一个根是,则方程有一个根是( )
A. B. C. D.
4.方程的解是,现给出另一个方程,它的解是( )
A. B. C. D.
5.关于x的方程有两个相等的实数根,若a,b,c是的三边长,则这个三角形一定是( ).
A.等边三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
6.已知是方程的一个根,则代数式的值应在( )
A.4和5之间 B.3和4之间 C.2和3之间 D.1和2之间
7.为加快推动生态巩义建设步伐,形成“城在林中、园在城中、山水相依,林路相随”的生态格局,市政府计划在某街心公园的一块矩形空地上修建草坪,如图,矩形长为40m,宽为30m,在矩形内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为,道路的宽度应为多少 设矩形地块四周道路的宽度为xm,根据题意,下列方程不正确的是( )
A. B.
C. D.
8.已知关于x的一元二次方程:,有下列结论:
①当时,方程有两个不相等的实根;
②当时,方程不可能有两个异号的实根;
③当时,方程的两个实根不可能都小于1;
④当时,方程的两个实根一个大于3,另一个小于3.
以上4个结论中,正确的个数为( )
A.1 B.2 C.3 D.4
9.已知关于x的方程x2﹣(a+2b)x+1=0有两个相等实数根.若在直角坐标系中,点P在直线l:y=﹣x+上,点Q(a,b)在直线l下方,则PQ的最小值为( )
A. B. C. D.
10.若四个互不相等的正实数a,b,c,d满足,,则的值为( )
A. B. C.2012 D.2011
二.填空题(共6小题,满分18分,每小题3分)
11.若关于的方程是一元二次方程,则 .
12.已知是一元二次方程的两个实数根,则使的值为整数的实数k的整数值为 .
13.一个三角形的两边长分别为3和5,其第三边是方程的根,则此三角形的周长为 .
14.关于的一元二次方程的两实数根分别为,且,则的值为 .
15.已知为实数,若,那么的值为 .
16.对于实数a、b,定义运算“*”; ,关于的方程恰好有三个不相等的实数根,则的取值范围是 .
三.解答题(共7小题,满分52分)
17.(6分)解方程:
(1) (2)
(3) (4)
18.(6分)已知关于的一元二次方程.
(1)请判断这个方程根的情况;
(2)若该方程有一个根小于1,求的取值范围.
19.(8分)如图为年月的日历表,在其中用一个方框圈出个数(如图中虚框所示),设这个数从小到大依次为,,,.
(1)若用含有的式子分别表示出,,,其结果应为:______;______;____;
(2)按这种方法所圈出的四个数中,的最大值为_______________;
(3)嘉嘉说:“按这种方法可以圈出四个数,使得的值为.”
淇淇说:“按这种方法可以圈出四个数,使最小数与最大数的乘积为.”
请你运用一元二次方程的相关知识分别说明二人的说法是否正确.
20.(8分)我们定义:如果关于x的一元二次方程有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.
(1)请判断方程是不是倍根方程,并说明理由;
(2)若是倍根方程,则___________.
21.(8分)第届世界杯足球赛已于年月日在卡塔尔开幕,其吉祥物“拉伊卜”也深受人们的喜爱.河南某超市在年月份售出个“拉伊卜”,随着世界杯开幕的临近,“拉伊卜”在之后两个月的销售量持续走高,在售价不变的基础上,月份的销售量达到了个.
(1)求“拉伊下”在,两个月销售量的月平均增长率;
(2)若每个“拉伊卜”的进价为元,原售价为元,该超市计划在年月进行降价促销,经调查发现,若“拉伊卜”的价格在原售价的基础上每降价元,销售量可在月份的基础上增加个,当每个“拉伊卜”降价多少元时,在月份出售“拉伊卜”可获利元?
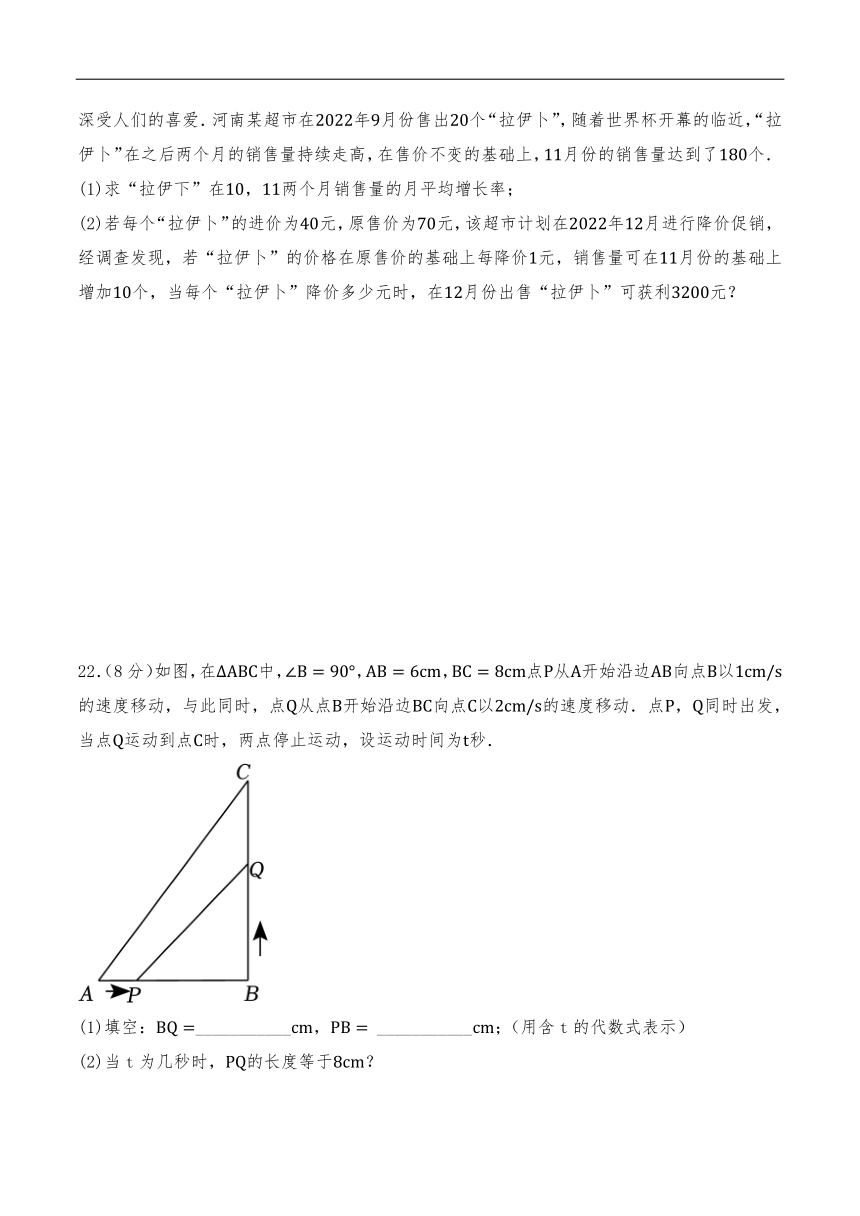
22.(8分)如图,在中,,,点从开始沿边向点以的速度移动,与此同时,点从点开始沿边向点以的速度移动.点,同时出发,当点运动到点时,两点停止运动,设运动时间为秒.
(1)填空:___________, ___________;(用含t的代数式表示)
(2)当t为几秒时,的长度等于?
(3)是否存在某一时刻t,使四边形的面积等于面积的?如果存在,求出t的值,如果不存在,请说明理由,
23.(8分)阅读材料:
材料1:若关于的一元二次方程的两个根为,则.
材料2:已知一元二次方程的两个实数根分别为,求的值.
解:∵一元二次方程的两个实数根分别为,
∴,,
则.
根据上述材料,结合你所学的知识,完成下列问题:
(1)材料理解:一元二次方程的两个根为,则_________, _________.
(2)类比应用:已知一元二次方程的两根分别为,求的值.
(3)思维拓展:已知实数满足,,且,求的值.
答案
一.选择题
1.C
【分析】逐项分析四个选项中一元二次方程根的判别式的符号,由此即可得出结论.
【详解】解:A.在中,,所以该方程有两个不相等的实数根,故A不符合题意;
B.在中,,所以该方程有两个不相等的实数根,故B不符合题意;
C.在中,,所以该方程有两个相等的实数根,故C符合题意;
D.将整理得:,,所以该方程有两个相等的实数根,故D不符合题意,
故选:C.
2.C
【分析】把代入方程求得,再解方程求得,将、的值代入求值即可.
【详解】解:将代入得:,
解得:,
的一元二次方程,
解得:,即,
将,代入,
得:,
故选:C.
3.C
【分析】利用一元二次方程的解,可得出,在等式的两边同时除以,可得出,进而可得出方程有一个根是.
【详解】关于的一元二次方程有一个根是,
,
在等式的两边同时除以得:,
方程有一个根是.
故选:C.
4.B
【分析】结合已知方程的解,利用换元法解一元二次方程即可得.
【详解】解:,
令,则方程可转化为,
由题意得:,
即,
解得,
故选:B.
5.B
【分析】由关于x的方程有两个相等的实数根,可得,整理得,根据勾股定理逆定理判断的形状即可.
【详解】解:∵关于x的方程有两个相等的实数根,
∴,整理得,
∴是直角三角形,
故选:B.
6.C
【分析】将a代入方程得,然后整体代入得结果,最后根据得范围确定结果的范围即可;
【详解】解:∵是方程的一个根,
∴将a代入方程,得:,
即:,
将上式代入中得:,
∵,
∴.
故选:C.
7.B
【分析】根据要使草坪的面积为,列一元二次方程,进一步判断即可.
【详解】解:可列方程,
故C选项不符合题意,
变形后,可得或,
故A选项不符合题意,D选项不符合题意,
不能得到,
故B选项符合题意,
故选:B.
8.C
【分析】根据一元二次方程根的判别式,一元二次方程根与系数的关系,一元二次方程的求根公式对每个选项进行一一判断即可.
【详解】解:∵,
∴Δ=4+4a,
∴①当时,Δ>0,方程有两个不相等的实根,故①正确,
②当时,两根之积,方程的两根异号,故②错误,
③方程的根为x=,
∵,
∴方程的两个实根不可能都小于1,故③正确,
④当时,由(3)可知,两个实根一个大于3,另一个小于3,故④正确,
故选:C.
9.A
【分析】先利用根判别式得到△=(a+2b)2﹣4=0,则a+2b=2或a+2b=-2,即点Q的坐标为(1-b,b)或(-1-b,b),如图:当点Q在直线y=-x-1上, EF为两直线的距离,最后求出EF得到PQ的最小值即可
【详解】解:∵关于x的方程x2﹣(a+2b)x+1=0有两个相等实数根,
∴△=(a+2b)2﹣4=0,
∴a+2b=2或a+2b=﹣2,
∵点Q(a,b),即Q(1﹣b,b)或(﹣1﹣b,b),
∴点Q所在的直线为y=﹣x+1或y=﹣x﹣1,
∵点Q(a,b)在直线y=﹣x+的下方,
∴点Q在直线y=﹣x﹣1上,如图,EF为两直线的距离,
∵OE=,OF=,
∴EF=,
∴PQ的最小值为.
故选:A.
10.A
【分析】根据题意可将a2012与b2012看做方程(x-c2012)(x-d2012)=2012的两个解,把所求的式子被减数利用积的乘方逆运算变形后换为x1x2,把方程整理后,利用根与系数的关系表示出x1x2,代入整理后的式子中,即可求出所求式子的值.
【详解】解:设a2012与b2012看做方程(x-c2012)(x-d2012)=2012的两个解,
方程整理得:x2-(c2012+d2012)x+(cd)2012-2012=0,
则(ab)2012-(cd)2012=x1x2 (cd)2012,
又x1x2=(cd)2012-2012,
则(ab)2012-(cd)2012=x1x2 (cd)2012=(cd)2012-2012-(cd)2012=-2012.
故选:A.
二.填空题
11.-1
【分析】根据一元二次方程的定义得出k 1≠0且|k|+1=2,再求出k即可.
【详解】解:∵关于x的方程是一元二次方程,
∴k 1≠0且|k|+1=2,
解得:k= 1,
故答案为: 1.
12.或或
【分析】根据一元二次方程根的判别式及根与系数的关系可进行求解.
【详解】解:由题意得:,且,
解得:,
由一元二次方程根与系数的关系可得:,,
∴,
∴或或2或或4或,
∴或或1或3或或,
∵,
∴或或;
故答案为或或.
13.13
【分析】因式分解法解方程可求得三角形的第三边,再根据三角形三边关系进行取舍即可求得答案.
【详解】解:解方程可得或,
当第三边为5时,则三角形的三边长为3、5、5,满足三角形三边关系,其周长为13;
当第三边为8时,则三角形的三边长为3、5、8,不满足三角形三边关系,舍去.
则此三角形的周长为13.
故答案为:13.
14.
【分析】根据一元二次方程根与系数的关系得到,结合已知求出,然后代入一元二次方程即可求出的值.
【详解】解:∵关于的一元二次方程的两实数根分别为,
∴,
∵,
∴,
∴,
把代入得:,
解得:,
故答案为:.
15.2或3
【分析】将原方程变形为,然后把看作一个整体运用因式分解法求出的值即可.
【详解】解:∵,
∴,
∴,
∴,
∴,
解解,,
故答案为:2或3.
16.
【分析】根据新定义的运算,分两种情况得出两个关于的一元二次方程,再由关于的方程恰好有三个实数根,得到关于的两个一元二次方程的根的情况,然后分情况讨论,确定t的取值范围.
【详解】解:由新定义的运算可得关于的方程为:
当时,即时,有,
即:,其根为:是负数,
当时,即,时,有,
即:,
要使关于的方程恰好有三个不相等的实数根,则和都必须有解,
∴,
∴,
(1)当时,即时,方程只有一个根,
∵当时,,
∴,,
∴此时方程只有一个根符合题意,
∴不符合题意;
(2)当时,方程的两个根都符合题题意,
∵当时,,
∴,,
∴方程只有一个根符合题意,
∴当时,恰好有三个不相等的实数根;
(3)∵当时,方程的一个根,另外一个根,
∴此时方程只有一个根符合题意,
∵,,
∴当时,方程最多有一个根符合题意,
∴当时不可能有三个不相等的实根;
综上分析可知,的取值范围是.
故答案为:.
三.解答题
17.(1)解:
∵,,,
∴,
,
(2)解:
∴
移项得:
∴
即
∴,
解得:,.
(3)解:
将原方程化为一般形式,得
这里,,.
,
(4)解:
原方程可变形为,
∴
∴或
解得:,.
18.(1)解:根据题意得:
,
∵无论取何值时,,
∴原方程有两个实数根;
(2)解:∵,
; ,
∵该方程有一个根小于1,
∴,
∴.
19.(1)解:同一行,左右相差,同列,上下相差,
∴,,,
∴答案是:,,.
(2)解:∵,
∴,
∵,
∴,
∴,即的最大值为.
(3)解:由(1)可知,,,
∴嘉嘉的说法是:,使得的值为,
∴,解方程得,,(舍去)
则虚框圈出的四个数应为 ,它在日历表中不存在,所以嘉嘉的说法不正确;
淇淇的说法是:,即,解方程得,,(舍去),
则虚线圈出的四个数为 ,在日历表中存在,所以淇淇的说法正确.
20.(1)解:方程是倍根方程,
理由如下:
由方程,
解得,,
,
方程是倍根方程;
(2)解:由方程,
解得,,
方程是倍根方程,
或,
得或,
故或,
故答案为:4或16.
21.(1)解:设“拉伊下”在,两个月销售量的月平均增长率为.
根据照意,得.
解得,(舍去).
.
答:“拉伊下”在,两个月销售量的月平均增长率为.
(2)设“拉伊卜”降价元时,在月份出售“拉伊卜”可获利元.
根据题意,得,
整理,得.
解得,(舍去).
答:当每个“拉伊卜”降价元时,在12月份出售“拉伊卜”可获利元.
22.(1)点从开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,
, ,
,
故答案为:,;
(2)由题意得,
,
解得:,(不合题意,舍去),
当时,的长等于;
(3)存在,理由如下:
若四边形的面积等于面积的,
的面积等于面积的,
,
,
解得:或,
当时,
当时,,四边形变为三角形,不合题意,舍去,
存在时刻,使四边形的面积等于面积的,的值为2.
23.(1)解:一元二次方程的两个根为,
,,
故答案为:,.
(2)解:一元二次方程的两根分别为、,
,,
.
(3)解:实数、满足,,
∴,看作是方程的两个实数根,
,,
.
一.选择题(共10小题,满分30分,每小题3分)
1.下列一元二次方程中,有两个相等的实数根的是( )
A. B.
C. D.
2.关于的一元二次方程的解为,,则代数式的值为( )
A.1 B.0 C. D.
3.已知关于的一元二次方程有一个根是,则方程有一个根是( )
A. B. C. D.
4.方程的解是,现给出另一个方程,它的解是( )
A. B. C. D.
5.关于x的方程有两个相等的实数根,若a,b,c是的三边长,则这个三角形一定是( ).
A.等边三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
6.已知是方程的一个根,则代数式的值应在( )
A.4和5之间 B.3和4之间 C.2和3之间 D.1和2之间
7.为加快推动生态巩义建设步伐,形成“城在林中、园在城中、山水相依,林路相随”的生态格局,市政府计划在某街心公园的一块矩形空地上修建草坪,如图,矩形长为40m,宽为30m,在矩形内的四周修筑同样宽的道路,余下的铺上草坪.要使草坪的面积为,道路的宽度应为多少 设矩形地块四周道路的宽度为xm,根据题意,下列方程不正确的是( )
A. B.
C. D.
8.已知关于x的一元二次方程:,有下列结论:
①当时,方程有两个不相等的实根;
②当时,方程不可能有两个异号的实根;
③当时,方程的两个实根不可能都小于1;
④当时,方程的两个实根一个大于3,另一个小于3.
以上4个结论中,正确的个数为( )
A.1 B.2 C.3 D.4
9.已知关于x的方程x2﹣(a+2b)x+1=0有两个相等实数根.若在直角坐标系中,点P在直线l:y=﹣x+上,点Q(a,b)在直线l下方,则PQ的最小值为( )
A. B. C. D.
10.若四个互不相等的正实数a,b,c,d满足,,则的值为( )
A. B. C.2012 D.2011
二.填空题(共6小题,满分18分,每小题3分)
11.若关于的方程是一元二次方程,则 .
12.已知是一元二次方程的两个实数根,则使的值为整数的实数k的整数值为 .
13.一个三角形的两边长分别为3和5,其第三边是方程的根,则此三角形的周长为 .
14.关于的一元二次方程的两实数根分别为,且,则的值为 .
15.已知为实数,若,那么的值为 .
16.对于实数a、b,定义运算“*”; ,关于的方程恰好有三个不相等的实数根,则的取值范围是 .
三.解答题(共7小题,满分52分)
17.(6分)解方程:
(1) (2)
(3) (4)
18.(6分)已知关于的一元二次方程.
(1)请判断这个方程根的情况;
(2)若该方程有一个根小于1,求的取值范围.
19.(8分)如图为年月的日历表,在其中用一个方框圈出个数(如图中虚框所示),设这个数从小到大依次为,,,.
(1)若用含有的式子分别表示出,,,其结果应为:______;______;____;
(2)按这种方法所圈出的四个数中,的最大值为_______________;
(3)嘉嘉说:“按这种方法可以圈出四个数,使得的值为.”
淇淇说:“按这种方法可以圈出四个数,使最小数与最大数的乘积为.”
请你运用一元二次方程的相关知识分别说明二人的说法是否正确.
20.(8分)我们定义:如果关于x的一元二次方程有两个实数根,且其中一个根为另一个根的2倍,则称这样的方程为“倍根方程”.
(1)请判断方程是不是倍根方程,并说明理由;
(2)若是倍根方程,则___________.
21.(8分)第届世界杯足球赛已于年月日在卡塔尔开幕,其吉祥物“拉伊卜”也深受人们的喜爱.河南某超市在年月份售出个“拉伊卜”,随着世界杯开幕的临近,“拉伊卜”在之后两个月的销售量持续走高,在售价不变的基础上,月份的销售量达到了个.
(1)求“拉伊下”在,两个月销售量的月平均增长率;
(2)若每个“拉伊卜”的进价为元,原售价为元,该超市计划在年月进行降价促销,经调查发现,若“拉伊卜”的价格在原售价的基础上每降价元,销售量可在月份的基础上增加个,当每个“拉伊卜”降价多少元时,在月份出售“拉伊卜”可获利元?
22.(8分)如图,在中,,,点从开始沿边向点以的速度移动,与此同时,点从点开始沿边向点以的速度移动.点,同时出发,当点运动到点时,两点停止运动,设运动时间为秒.
(1)填空:___________, ___________;(用含t的代数式表示)
(2)当t为几秒时,的长度等于?
(3)是否存在某一时刻t,使四边形的面积等于面积的?如果存在,求出t的值,如果不存在,请说明理由,
23.(8分)阅读材料:
材料1:若关于的一元二次方程的两个根为,则.
材料2:已知一元二次方程的两个实数根分别为,求的值.
解:∵一元二次方程的两个实数根分别为,
∴,,
则.
根据上述材料,结合你所学的知识,完成下列问题:
(1)材料理解:一元二次方程的两个根为,则_________, _________.
(2)类比应用:已知一元二次方程的两根分别为,求的值.
(3)思维拓展:已知实数满足,,且,求的值.
答案
一.选择题
1.C
【分析】逐项分析四个选项中一元二次方程根的判别式的符号,由此即可得出结论.
【详解】解:A.在中,,所以该方程有两个不相等的实数根,故A不符合题意;
B.在中,,所以该方程有两个不相等的实数根,故B不符合题意;
C.在中,,所以该方程有两个相等的实数根,故C符合题意;
D.将整理得:,,所以该方程有两个相等的实数根,故D不符合题意,
故选:C.
2.C
【分析】把代入方程求得,再解方程求得,将、的值代入求值即可.
【详解】解:将代入得:,
解得:,
的一元二次方程,
解得:,即,
将,代入,
得:,
故选:C.
3.C
【分析】利用一元二次方程的解,可得出,在等式的两边同时除以,可得出,进而可得出方程有一个根是.
【详解】关于的一元二次方程有一个根是,
,
在等式的两边同时除以得:,
方程有一个根是.
故选:C.
4.B
【分析】结合已知方程的解,利用换元法解一元二次方程即可得.
【详解】解:,
令,则方程可转化为,
由题意得:,
即,
解得,
故选:B.
5.B
【分析】由关于x的方程有两个相等的实数根,可得,整理得,根据勾股定理逆定理判断的形状即可.
【详解】解:∵关于x的方程有两个相等的实数根,
∴,整理得,
∴是直角三角形,
故选:B.
6.C
【分析】将a代入方程得,然后整体代入得结果,最后根据得范围确定结果的范围即可;
【详解】解:∵是方程的一个根,
∴将a代入方程,得:,
即:,
将上式代入中得:,
∵,
∴.
故选:C.
7.B
【分析】根据要使草坪的面积为,列一元二次方程,进一步判断即可.
【详解】解:可列方程,
故C选项不符合题意,
变形后,可得或,
故A选项不符合题意,D选项不符合题意,
不能得到,
故B选项符合题意,
故选:B.
8.C
【分析】根据一元二次方程根的判别式,一元二次方程根与系数的关系,一元二次方程的求根公式对每个选项进行一一判断即可.
【详解】解:∵,
∴Δ=4+4a,
∴①当时,Δ>0,方程有两个不相等的实根,故①正确,
②当时,两根之积,方程的两根异号,故②错误,
③方程的根为x=,
∵,
∴方程的两个实根不可能都小于1,故③正确,
④当时,由(3)可知,两个实根一个大于3,另一个小于3,故④正确,
故选:C.
9.A
【分析】先利用根判别式得到△=(a+2b)2﹣4=0,则a+2b=2或a+2b=-2,即点Q的坐标为(1-b,b)或(-1-b,b),如图:当点Q在直线y=-x-1上, EF为两直线的距离,最后求出EF得到PQ的最小值即可
【详解】解:∵关于x的方程x2﹣(a+2b)x+1=0有两个相等实数根,
∴△=(a+2b)2﹣4=0,
∴a+2b=2或a+2b=﹣2,
∵点Q(a,b),即Q(1﹣b,b)或(﹣1﹣b,b),
∴点Q所在的直线为y=﹣x+1或y=﹣x﹣1,
∵点Q(a,b)在直线y=﹣x+的下方,
∴点Q在直线y=﹣x﹣1上,如图,EF为两直线的距离,
∵OE=,OF=,
∴EF=,
∴PQ的最小值为.
故选:A.
10.A
【分析】根据题意可将a2012与b2012看做方程(x-c2012)(x-d2012)=2012的两个解,把所求的式子被减数利用积的乘方逆运算变形后换为x1x2,把方程整理后,利用根与系数的关系表示出x1x2,代入整理后的式子中,即可求出所求式子的值.
【详解】解:设a2012与b2012看做方程(x-c2012)(x-d2012)=2012的两个解,
方程整理得:x2-(c2012+d2012)x+(cd)2012-2012=0,
则(ab)2012-(cd)2012=x1x2 (cd)2012,
又x1x2=(cd)2012-2012,
则(ab)2012-(cd)2012=x1x2 (cd)2012=(cd)2012-2012-(cd)2012=-2012.
故选:A.
二.填空题
11.-1
【分析】根据一元二次方程的定义得出k 1≠0且|k|+1=2,再求出k即可.
【详解】解:∵关于x的方程是一元二次方程,
∴k 1≠0且|k|+1=2,
解得:k= 1,
故答案为: 1.
12.或或
【分析】根据一元二次方程根的判别式及根与系数的关系可进行求解.
【详解】解:由题意得:,且,
解得:,
由一元二次方程根与系数的关系可得:,,
∴,
∴或或2或或4或,
∴或或1或3或或,
∵,
∴或或;
故答案为或或.
13.13
【分析】因式分解法解方程可求得三角形的第三边,再根据三角形三边关系进行取舍即可求得答案.
【详解】解:解方程可得或,
当第三边为5时,则三角形的三边长为3、5、5,满足三角形三边关系,其周长为13;
当第三边为8时,则三角形的三边长为3、5、8,不满足三角形三边关系,舍去.
则此三角形的周长为13.
故答案为:13.
14.
【分析】根据一元二次方程根与系数的关系得到,结合已知求出,然后代入一元二次方程即可求出的值.
【详解】解:∵关于的一元二次方程的两实数根分别为,
∴,
∵,
∴,
∴,
把代入得:,
解得:,
故答案为:.
15.2或3
【分析】将原方程变形为,然后把看作一个整体运用因式分解法求出的值即可.
【详解】解:∵,
∴,
∴,
∴,
∴,
解解,,
故答案为:2或3.
16.
【分析】根据新定义的运算,分两种情况得出两个关于的一元二次方程,再由关于的方程恰好有三个实数根,得到关于的两个一元二次方程的根的情况,然后分情况讨论,确定t的取值范围.
【详解】解:由新定义的运算可得关于的方程为:
当时,即时,有,
即:,其根为:是负数,
当时,即,时,有,
即:,
要使关于的方程恰好有三个不相等的实数根,则和都必须有解,
∴,
∴,
(1)当时,即时,方程只有一个根,
∵当时,,
∴,,
∴此时方程只有一个根符合题意,
∴不符合题意;
(2)当时,方程的两个根都符合题题意,
∵当时,,
∴,,
∴方程只有一个根符合题意,
∴当时,恰好有三个不相等的实数根;
(3)∵当时,方程的一个根,另外一个根,
∴此时方程只有一个根符合题意,
∵,,
∴当时,方程最多有一个根符合题意,
∴当时不可能有三个不相等的实根;
综上分析可知,的取值范围是.
故答案为:.
三.解答题
17.(1)解:
∵,,,
∴,
,
(2)解:
∴
移项得:
∴
即
∴,
解得:,.
(3)解:
将原方程化为一般形式,得
这里,,.
,
(4)解:
原方程可变形为,
∴
∴或
解得:,.
18.(1)解:根据题意得:
,
∵无论取何值时,,
∴原方程有两个实数根;
(2)解:∵,
; ,
∵该方程有一个根小于1,
∴,
∴.
19.(1)解:同一行,左右相差,同列,上下相差,
∴,,,
∴答案是:,,.
(2)解:∵,
∴,
∵,
∴,
∴,即的最大值为.
(3)解:由(1)可知,,,
∴嘉嘉的说法是:,使得的值为,
∴,解方程得,,(舍去)
则虚框圈出的四个数应为 ,它在日历表中不存在,所以嘉嘉的说法不正确;
淇淇的说法是:,即,解方程得,,(舍去),
则虚线圈出的四个数为 ,在日历表中存在,所以淇淇的说法正确.
20.(1)解:方程是倍根方程,
理由如下:
由方程,
解得,,
,
方程是倍根方程;
(2)解:由方程,
解得,,
方程是倍根方程,
或,
得或,
故或,
故答案为:4或16.
21.(1)解:设“拉伊下”在,两个月销售量的月平均增长率为.
根据照意,得.
解得,(舍去).
.
答:“拉伊下”在,两个月销售量的月平均增长率为.
(2)设“拉伊卜”降价元时,在月份出售“拉伊卜”可获利元.
根据题意,得,
整理,得.
解得,(舍去).
答:当每个“拉伊卜”降价元时,在12月份出售“拉伊卜”可获利元.
22.(1)点从开始沿边向点以的速度移动,点从点开始沿边向点以的速度移动,
, ,
,
故答案为:,;
(2)由题意得,
,
解得:,(不合题意,舍去),
当时,的长等于;
(3)存在,理由如下:
若四边形的面积等于面积的,
的面积等于面积的,
,
,
解得:或,
当时,
当时,,四边形变为三角形,不合题意,舍去,
存在时刻,使四边形的面积等于面积的,的值为2.
23.(1)解:一元二次方程的两个根为,
,,
故答案为:,.
(2)解:一元二次方程的两根分别为、,
,,
.
(3)解:实数、满足,,
∴,看作是方程的两个实数根,
,,
.
