人教版小学数学五年级上册第六单元《多边形的面积》作业设计
文档属性
| 名称 | 人教版小学数学五年级上册第六单元《多边形的面积》作业设计 |  | |
| 格式 | docx | ||
| 文件大小 | 175.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 13:18:20 | ||
图片预览

文档简介
小学数学五年级上册第六单元《多边形的面积》作业设计
一、单元内容
基本 信息 学科 年级 学期 教材版本 单元名称
数学 五年级 第一学期 人教版 多边形的面积
课时 信息 序号 课时名称 对应教材内容
1 平行四边形的面积 例1(P87-91)
2 三角形的面积 例2(P92-95)
3 梯形的面积 例3(P96-99)
二、单元教学目标
关注整体学生的数学核心素养的落实,关注不同学生的个体差异,让不同层次、不同学习能力的学生都能有收获,有成长,有成就感。具体如下:
1. 通过作业活动,巩固并掌握多边形的面积计算公式,通过作业练习,探索各图形之间的联系,进一步理解“转化”这一重要的数学思想。
2. 通过动手操作、画图、表达等策略,能熟练运用公式计算平行四边形、三角形和梯形的面积;能利用多边形面积的计算公式解决生活中的实际问题。
3. 在完成作业的过程中,体会解决问题方法的多样性,能根据自身知识基础、擅长领域和个人能力等实际情况,选择适当的练习、合适的方法灵活思考并解决问题,培养学生的发散思维能力。
4. 通过作业活动,能正确评价自己和他人,提高对“空间与图形”内容的学习兴趣,逐步形成积极的数学情感。
三、作业设计思路与分析
在“双减”政策的指导下,依据学生情况,围绕本单元作业的目标、内容、类型、难度和数量等要素,以符合学生学习规律、体现素质教育为导向的基础性作业为主;贯穿探究性、实践性和跨学科综合作业,并利用信息化等手段不断提升作业的科学性与有效性。根据学段、学科特点及学生实际需要和完成能力,合理布置书面作业、科学探究、实际应用等不同类型作业。
作业思路:旨在提供给学生数学思想方法,培养学生数学的思维能力,提高学生的数学素质。在教学中,数学知识是一条明线,得到数学教师的重视,数学思想方法是一条暗线,容易被教师所忽视。但数学思想方法渗透比学习知识更重要,因为这是数学的精髓和灵魂。教给学生思考方法、学习方法和解决问题的方法,为学生未来发展服务,让学生在脑海里留下数学意识,长期下去,学生将终身受用。在出题时,注意进行转化思想的渗透,做到以基础知识为主,适当加以延伸,发散学生思维,兼顾不同层次学生的发展;紧密联系生活实际激活学生已有生活经验;注重让学生经历问题解决的过程,培养学生解决问题的策略,提升学生解决问题的能力;加强知识之间的联系与沟通,培养学生迁移类推的能力;结合生活实际,适当丰富学习素材,增强学生应用知识数学的意识。
四、作业设计
一、《梯形的面积》课时作业
(一)基础作业
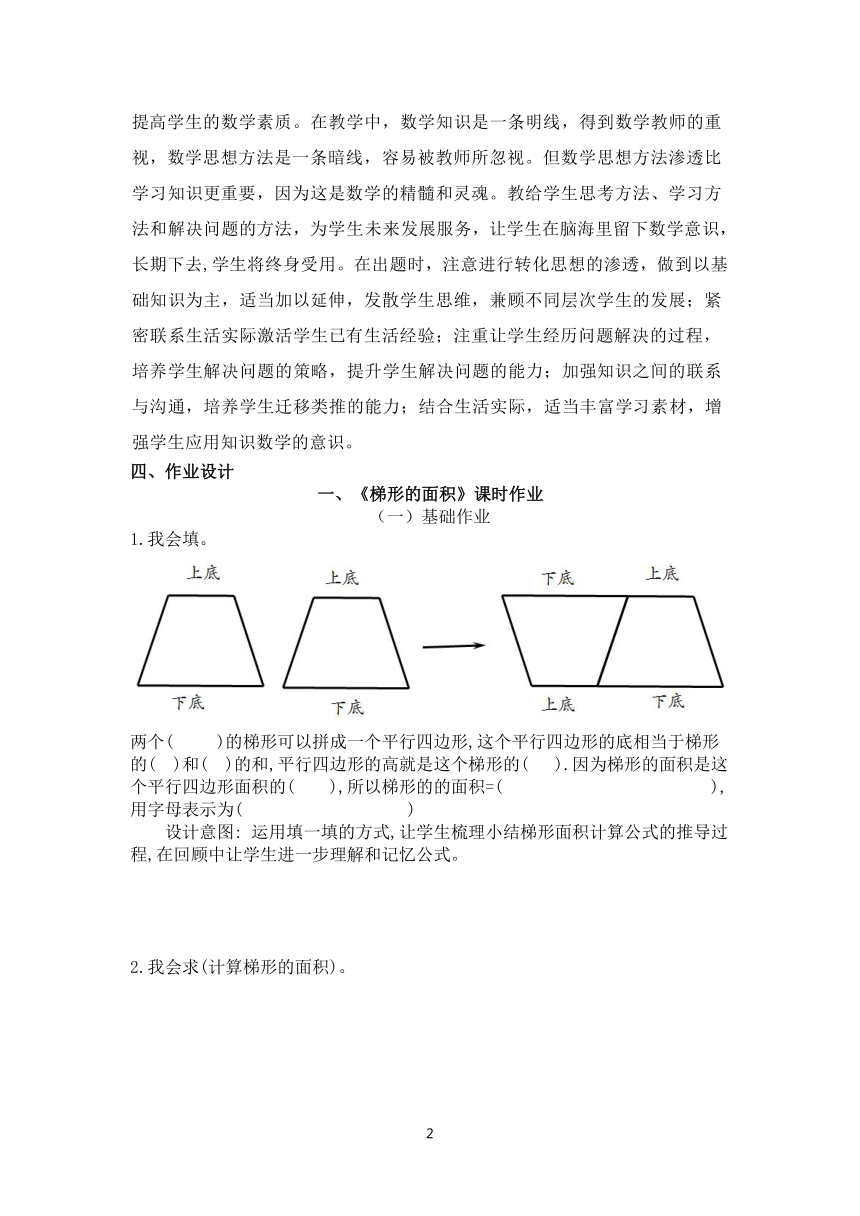
1.我会填。
两个( )的梯形可以拼成一个平行四边形,这个平行四边形的底相当于梯形的( )和( )的和,平行四边形的高就是这个梯形的( ).因为梯形的面积是这个平行四边形面积的( ),所以梯形的的面积=( ),
用字母表示为( )
设计意图: 运用填一填的方式,让学生梳理小结梯形面积计算公式的推导过程,在回顾中让学生进一步理解和记忆公式。
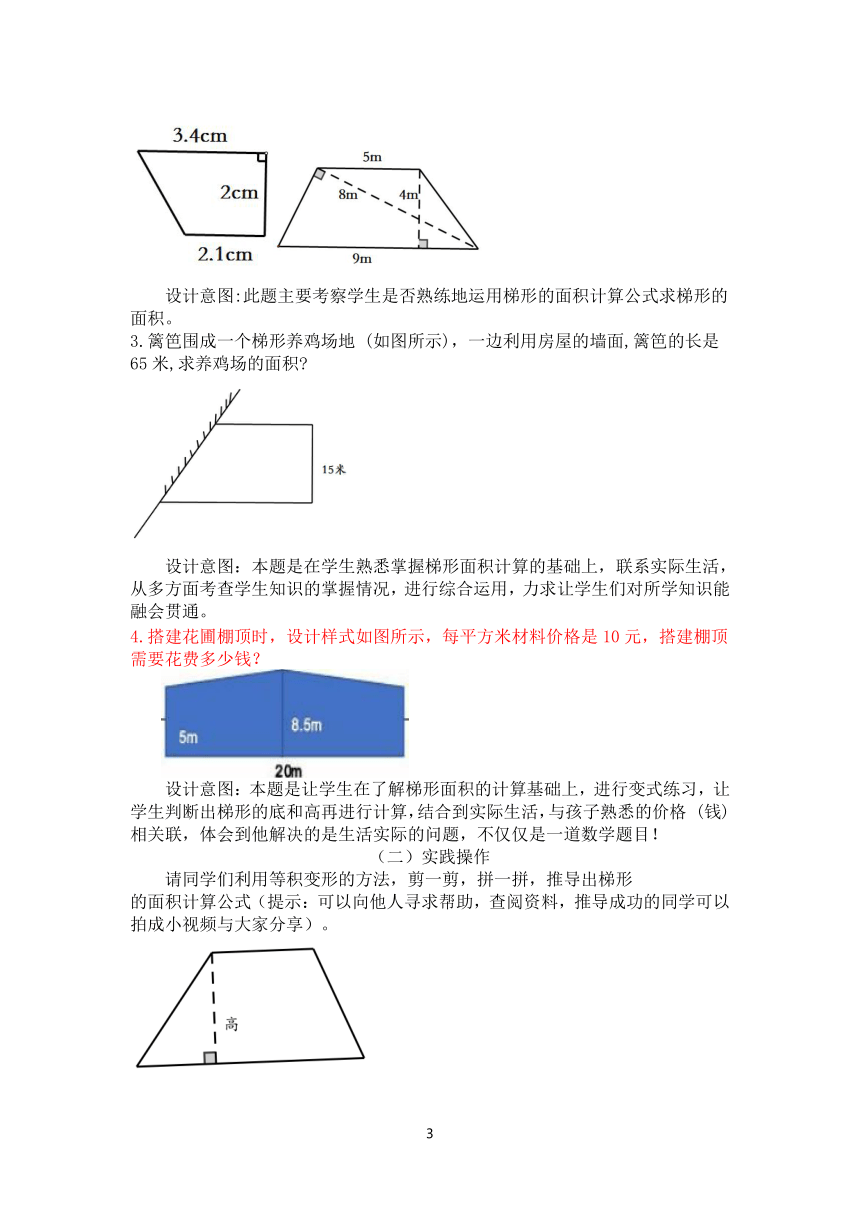
2.我会求(计算梯形的面积)。
设计意图:此题主要考察学生是否熟练地运用梯形的面积计算公式求梯形的面积。
3.篱笆围成一个梯形养鸡场地 (如图所示),一边利用房屋的墙面,篱笆的长是65米,求养鸡场的面积
设计意图:本题是在学生熟悉掌握梯形面积计算的基础上,联系实际生活,从多方面考查学生知识的掌握情况,进行综合运用,力求让学生们对所学知识能融会贯通。
4.搭建花圃棚顶时,设计样式如图所示,每平方米材料价格是10元,搭建棚顶需要花费多少钱?
设计意图:本题是让学生在了解梯形面积的计算基础上,进行变式练习,让学生判断出梯形的底和高再进行计算,结合到实际生活,与孩子熟悉的价格 (钱) 相关联,体会到他解决的是生活实际的问题,不仅仅是一道数学题目!
(二)实践操作
请同学们利用等积变形的方法,剪一剪,拼一拼,推导出梯形
的面积计算公式(提示:可以向他人寻求帮助,查阅资料,推导成功的同学可以拍成小视频与大家分享)。
设计意图:通过实践操作,可以使学生更深刻理解梯形面积计算公式,让学有余力的学生进行适当的拓展,加强学生的创新意识,并且家长参与到孩子的作业过程中,不仅对孩子的学习是一种促进,更是亲子交流的过程。
二、《多边形的面积》单元检测作业
(一)学以致用(基础性作业)
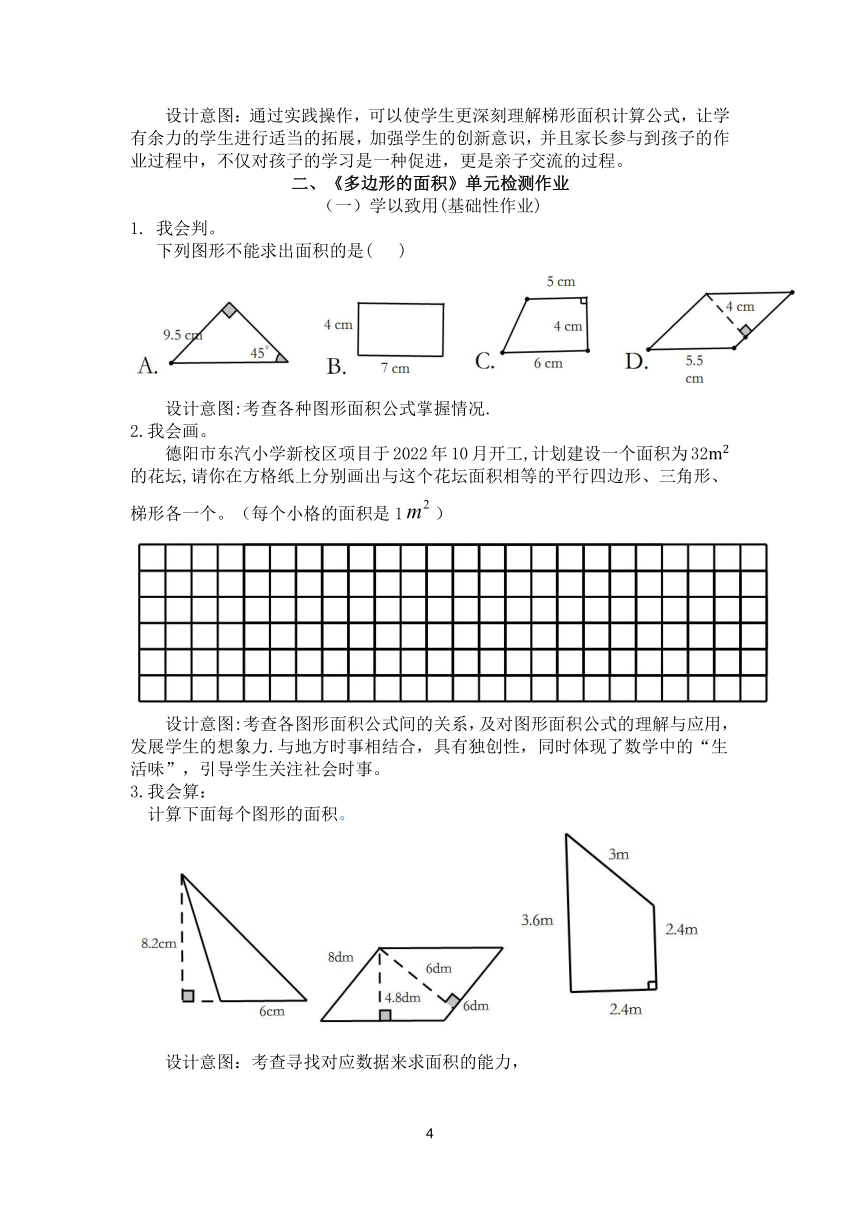
我会判。
下列图形不能求出面积的是( )
设计意图:考查各种图形面积公式掌握情况.
2.我会画。
德阳市东汽小学新校区项目于2022年10月开工,计划建设一个面积为32的花坛,请你在方格纸上分别画出与这个花坛面积相等的平行四边形、三角形、梯形各一个。(每个小格的面积是1)
设计意图:考查各图形面积公式间的关系,及对图形面积公式的理解与应用,发展学生的想象力.与地方时事相结合,具有独创性,同时体现了数学中的“生活味”,引导学生关注社会时事。
3.我会算:
计算下面每个图形的面积。
设计意图:考查寻找对应数据来求面积的能力,
4.我会选:
(1)如图,已知三角形ABC的面积是37.5,那么每个方格的面积是( )
A. 1 B. 2.5 C. 5 D. 25
(2)如图,一个长方形框架拉成平行四边形后,面积是24平方分米,长方形的周长是( )分米。
A.12 B.16 C.24 D.36
设计意图:关注面积计算公式的推导过程,会逆运用计算公式,能理解图形部分之间的联系.
我会说。
这个单元我们学行四边形、三角形和梯形的面积计算公式。请你任选一种图形,用文字结合图形的方法表达它的面积公式推导过程。
设计意图:关注推理能力,让学生在“画数学”的过程中能清晰、有条理的表达自己思考的过程。
6.我会用:
科学乐园有一块梯形空地,要分给3个班种蔬菜。四(1)班种西红柿,四(2)班种茄子,四(3)班种辣椒。
三个班分到菜地面积相同吗?
如果1种9株辣椒,一共需要多少株辣椒?
如果1株西红柿苗占地0.2,一共需要多少株西红柿苗?
如果共收603千克的茄子,平均1收多少千克的茄子。
设计意图:本题将多边形面积的计算植入生活载体中,激发学生的解题兴趣,一定程度上培养学生丰富的想象力、应用意识和创新意识。题目的数据特征有助于学生求出面积后,更快发现背后隐含的关系。这样的综合练习让学生在解决实际问题中提升应用能力。
(二)举一反三(发展性作业)
善于说理
(1)如图,在两个相同的长方形中,各画一个三角形(阴影部分),请你用字母、文字或算式比较S1和S2的大小关系.
(2)已知一个三角形的面积和底(如下图),求高。
小明是这样列式:
小红是这样列式:
他们的方法正确吗 请说明理由。(可以借助画图、算式等形式,选你喜欢的算式说明理由,)
设计意图:关注推理能力,在提高学生观察能力的同时,培养学生对图形的分析能力,发展几何直观。
2、善于思考:
在直角梯形ABDE中,AE=6cm,BD=10cm,梯形ABCE的面积等于三角形ECD的面积,求BC的长?
设计意图:本题帮助学生巩固和强化平行线之间等高等面积梯形“上底与下底的和始终不变”的特点,进一步深化平面图形之间的等积变形,感悟转化思想,发展高阶思维。
(三)拓展提升(探究性作业)
(1)
图形 ① ② ③ ④ ⑤
公式 (文字)
面积/
从上表中,你发现了什么?
(3)请你用梯形的面积公式计算出上面所有图形的面积,你又发现了什么?
② ③
④ ⑤
我的发现:
设计意图:本题借助用梯形的面积公式计算出上面所有图形的面积,发现梯形的面积与三角形、平行四边形、正方形面积之间的关系。沟通了图形面积之间的联系,形成以梯形面积公式为“通式”的结构图示,渗透转化思想,感受数学思想方法的魅力。
修改情况的相关说明
(一)梯形的面积课时作业
梯形ABCD的面积是100cm ,BC=20cm,DF=8cm,求阴影部分的面积是多少?
【修改说明】原本设计的提升题如上,主要考察对梯形面积公式的逆用,关键在于用a=2S÷h-b求上底。对刚学习了梯形面积公式的学生来说,逆用公式难度太大,一些学生也没有运用方程解决问题的意识。部分学生通过算式或方程求出上底再求面积;少部分学生作辅助线将BD相连,用平行四边形的面积减三角形BDC的面积求得阴影部分面积的一半;有53%的小朋友在这道题上出错,因此删除此题,改成了以下的实际应用题(即第4题)。
4.搭建花圃棚顶时,设计样式如图所示,每平方米材料价格是10元,搭建棚顶需要花费多少钱?
【修改意图】作业的设计不仅要定位于“知识的巩固”和“技能的强化”,同时要尊重学生的个体差异,注重开放性的训练。这道题目加强了数学内容与学生生活的联系,考察学生提取数学信息的能力、对梯形面积公式的运用,可以将其看成两个上底为5m、下底为8.5m、高为10m的梯形面积之和,也可以通过旋转和平移将其转化为求长13.5m (5+8.5)、宽10m的长方形面积,再计算总价,达到“一题多解”的目的,留给学生创新、发现的余地,对学生的思维进行求“新”、求“全”、求“活”的调控。
单元检测作业中,
《多边形的面积》单元检测作业
在第二部分:举一反三(发展性作业)中,原本设计如下:
大胆创造:两条对角线把梯形ABCD分割成四个三角形,如图所示,已知两个三角形的面积,求另两个三角形的面积各是多少?
【修改说明】这道题目给出的只有面积数据,需要学生通过“同底等高的三角形面积相等”推理出三角形AOC和DOC的面积相等,再通过“等高的两个三角形,底之比等于面积之比”推理出三角形AOD的面积等于AOB面积的1/2。整个题目不给具体的底和高数据,两次通过面积之比推理,难度太大,已超出学生用已有知识解决问题的能力范围,因此删除此题,改成了以下的题目(即第2题)。
2.善于思考:
在直角梯形ABDE中,AE=6cm,BD=10cm,梯形ABCE的面积等于三角形ECD的面积,求BC的长?
【修改意图】本题给出了上下底数据,帮助学生巩固和强化平行线之间等高等面积梯形“上底与下底的和始终不变”的特点,对学生来说有适当的难度,但又留出了适当的突破口,比较适合作为拓展题出现。
一、单元内容
基本 信息 学科 年级 学期 教材版本 单元名称
数学 五年级 第一学期 人教版 多边形的面积
课时 信息 序号 课时名称 对应教材内容
1 平行四边形的面积 例1(P87-91)
2 三角形的面积 例2(P92-95)
3 梯形的面积 例3(P96-99)
二、单元教学目标
关注整体学生的数学核心素养的落实,关注不同学生的个体差异,让不同层次、不同学习能力的学生都能有收获,有成长,有成就感。具体如下:
1. 通过作业活动,巩固并掌握多边形的面积计算公式,通过作业练习,探索各图形之间的联系,进一步理解“转化”这一重要的数学思想。
2. 通过动手操作、画图、表达等策略,能熟练运用公式计算平行四边形、三角形和梯形的面积;能利用多边形面积的计算公式解决生活中的实际问题。
3. 在完成作业的过程中,体会解决问题方法的多样性,能根据自身知识基础、擅长领域和个人能力等实际情况,选择适当的练习、合适的方法灵活思考并解决问题,培养学生的发散思维能力。
4. 通过作业活动,能正确评价自己和他人,提高对“空间与图形”内容的学习兴趣,逐步形成积极的数学情感。
三、作业设计思路与分析
在“双减”政策的指导下,依据学生情况,围绕本单元作业的目标、内容、类型、难度和数量等要素,以符合学生学习规律、体现素质教育为导向的基础性作业为主;贯穿探究性、实践性和跨学科综合作业,并利用信息化等手段不断提升作业的科学性与有效性。根据学段、学科特点及学生实际需要和完成能力,合理布置书面作业、科学探究、实际应用等不同类型作业。
作业思路:旨在提供给学生数学思想方法,培养学生数学的思维能力,提高学生的数学素质。在教学中,数学知识是一条明线,得到数学教师的重视,数学思想方法是一条暗线,容易被教师所忽视。但数学思想方法渗透比学习知识更重要,因为这是数学的精髓和灵魂。教给学生思考方法、学习方法和解决问题的方法,为学生未来发展服务,让学生在脑海里留下数学意识,长期下去,学生将终身受用。在出题时,注意进行转化思想的渗透,做到以基础知识为主,适当加以延伸,发散学生思维,兼顾不同层次学生的发展;紧密联系生活实际激活学生已有生活经验;注重让学生经历问题解决的过程,培养学生解决问题的策略,提升学生解决问题的能力;加强知识之间的联系与沟通,培养学生迁移类推的能力;结合生活实际,适当丰富学习素材,增强学生应用知识数学的意识。
四、作业设计
一、《梯形的面积》课时作业
(一)基础作业
1.我会填。
两个( )的梯形可以拼成一个平行四边形,这个平行四边形的底相当于梯形的( )和( )的和,平行四边形的高就是这个梯形的( ).因为梯形的面积是这个平行四边形面积的( ),所以梯形的的面积=( ),
用字母表示为( )
设计意图: 运用填一填的方式,让学生梳理小结梯形面积计算公式的推导过程,在回顾中让学生进一步理解和记忆公式。
2.我会求(计算梯形的面积)。
设计意图:此题主要考察学生是否熟练地运用梯形的面积计算公式求梯形的面积。
3.篱笆围成一个梯形养鸡场地 (如图所示),一边利用房屋的墙面,篱笆的长是65米,求养鸡场的面积
设计意图:本题是在学生熟悉掌握梯形面积计算的基础上,联系实际生活,从多方面考查学生知识的掌握情况,进行综合运用,力求让学生们对所学知识能融会贯通。
4.搭建花圃棚顶时,设计样式如图所示,每平方米材料价格是10元,搭建棚顶需要花费多少钱?
设计意图:本题是让学生在了解梯形面积的计算基础上,进行变式练习,让学生判断出梯形的底和高再进行计算,结合到实际生活,与孩子熟悉的价格 (钱) 相关联,体会到他解决的是生活实际的问题,不仅仅是一道数学题目!
(二)实践操作
请同学们利用等积变形的方法,剪一剪,拼一拼,推导出梯形
的面积计算公式(提示:可以向他人寻求帮助,查阅资料,推导成功的同学可以拍成小视频与大家分享)。
设计意图:通过实践操作,可以使学生更深刻理解梯形面积计算公式,让学有余力的学生进行适当的拓展,加强学生的创新意识,并且家长参与到孩子的作业过程中,不仅对孩子的学习是一种促进,更是亲子交流的过程。
二、《多边形的面积》单元检测作业
(一)学以致用(基础性作业)
我会判。
下列图形不能求出面积的是( )
设计意图:考查各种图形面积公式掌握情况.
2.我会画。
德阳市东汽小学新校区项目于2022年10月开工,计划建设一个面积为32的花坛,请你在方格纸上分别画出与这个花坛面积相等的平行四边形、三角形、梯形各一个。(每个小格的面积是1)
设计意图:考查各图形面积公式间的关系,及对图形面积公式的理解与应用,发展学生的想象力.与地方时事相结合,具有独创性,同时体现了数学中的“生活味”,引导学生关注社会时事。
3.我会算:
计算下面每个图形的面积。
设计意图:考查寻找对应数据来求面积的能力,
4.我会选:
(1)如图,已知三角形ABC的面积是37.5,那么每个方格的面积是( )
A. 1 B. 2.5 C. 5 D. 25
(2)如图,一个长方形框架拉成平行四边形后,面积是24平方分米,长方形的周长是( )分米。
A.12 B.16 C.24 D.36
设计意图:关注面积计算公式的推导过程,会逆运用计算公式,能理解图形部分之间的联系.
我会说。
这个单元我们学行四边形、三角形和梯形的面积计算公式。请你任选一种图形,用文字结合图形的方法表达它的面积公式推导过程。
设计意图:关注推理能力,让学生在“画数学”的过程中能清晰、有条理的表达自己思考的过程。
6.我会用:
科学乐园有一块梯形空地,要分给3个班种蔬菜。四(1)班种西红柿,四(2)班种茄子,四(3)班种辣椒。
三个班分到菜地面积相同吗?
如果1种9株辣椒,一共需要多少株辣椒?
如果1株西红柿苗占地0.2,一共需要多少株西红柿苗?
如果共收603千克的茄子,平均1收多少千克的茄子。
设计意图:本题将多边形面积的计算植入生活载体中,激发学生的解题兴趣,一定程度上培养学生丰富的想象力、应用意识和创新意识。题目的数据特征有助于学生求出面积后,更快发现背后隐含的关系。这样的综合练习让学生在解决实际问题中提升应用能力。
(二)举一反三(发展性作业)
善于说理
(1)如图,在两个相同的长方形中,各画一个三角形(阴影部分),请你用字母、文字或算式比较S1和S2的大小关系.
(2)已知一个三角形的面积和底(如下图),求高。
小明是这样列式:
小红是这样列式:
他们的方法正确吗 请说明理由。(可以借助画图、算式等形式,选你喜欢的算式说明理由,)
设计意图:关注推理能力,在提高学生观察能力的同时,培养学生对图形的分析能力,发展几何直观。
2、善于思考:
在直角梯形ABDE中,AE=6cm,BD=10cm,梯形ABCE的面积等于三角形ECD的面积,求BC的长?
设计意图:本题帮助学生巩固和强化平行线之间等高等面积梯形“上底与下底的和始终不变”的特点,进一步深化平面图形之间的等积变形,感悟转化思想,发展高阶思维。
(三)拓展提升(探究性作业)
(1)
图形 ① ② ③ ④ ⑤
公式 (文字)
面积/
从上表中,你发现了什么?
(3)请你用梯形的面积公式计算出上面所有图形的面积,你又发现了什么?
② ③
④ ⑤
我的发现:
设计意图:本题借助用梯形的面积公式计算出上面所有图形的面积,发现梯形的面积与三角形、平行四边形、正方形面积之间的关系。沟通了图形面积之间的联系,形成以梯形面积公式为“通式”的结构图示,渗透转化思想,感受数学思想方法的魅力。
修改情况的相关说明
(一)梯形的面积课时作业
梯形ABCD的面积是100cm ,BC=20cm,DF=8cm,求阴影部分的面积是多少?
【修改说明】原本设计的提升题如上,主要考察对梯形面积公式的逆用,关键在于用a=2S÷h-b求上底。对刚学习了梯形面积公式的学生来说,逆用公式难度太大,一些学生也没有运用方程解决问题的意识。部分学生通过算式或方程求出上底再求面积;少部分学生作辅助线将BD相连,用平行四边形的面积减三角形BDC的面积求得阴影部分面积的一半;有53%的小朋友在这道题上出错,因此删除此题,改成了以下的实际应用题(即第4题)。
4.搭建花圃棚顶时,设计样式如图所示,每平方米材料价格是10元,搭建棚顶需要花费多少钱?
【修改意图】作业的设计不仅要定位于“知识的巩固”和“技能的强化”,同时要尊重学生的个体差异,注重开放性的训练。这道题目加强了数学内容与学生生活的联系,考察学生提取数学信息的能力、对梯形面积公式的运用,可以将其看成两个上底为5m、下底为8.5m、高为10m的梯形面积之和,也可以通过旋转和平移将其转化为求长13.5m (5+8.5)、宽10m的长方形面积,再计算总价,达到“一题多解”的目的,留给学生创新、发现的余地,对学生的思维进行求“新”、求“全”、求“活”的调控。
单元检测作业中,
《多边形的面积》单元检测作业
在第二部分:举一反三(发展性作业)中,原本设计如下:
大胆创造:两条对角线把梯形ABCD分割成四个三角形,如图所示,已知两个三角形的面积,求另两个三角形的面积各是多少?
【修改说明】这道题目给出的只有面积数据,需要学生通过“同底等高的三角形面积相等”推理出三角形AOC和DOC的面积相等,再通过“等高的两个三角形,底之比等于面积之比”推理出三角形AOD的面积等于AOB面积的1/2。整个题目不给具体的底和高数据,两次通过面积之比推理,难度太大,已超出学生用已有知识解决问题的能力范围,因此删除此题,改成了以下的题目(即第2题)。
2.善于思考:
在直角梯形ABDE中,AE=6cm,BD=10cm,梯形ABCE的面积等于三角形ECD的面积,求BC的长?
【修改意图】本题给出了上下底数据,帮助学生巩固和强化平行线之间等高等面积梯形“上底与下底的和始终不变”的特点,对学生来说有适当的难度,但又留出了适当的突破口,比较适合作为拓展题出现。
