人教八年级上册13.4最短路径问题教学设计(表格式)
文档属性
| 名称 | 人教八年级上册13.4最短路径问题教学设计(表格式) |  | |
| 格式 | docx | ||
| 文件大小 | 275.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 17:18:50 | ||
图片预览

文档简介
教学设计
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 最短路径问题
教科书 书 名:初中数学 出版社:人民教育出版社
教学目标
1.熟悉常见的解决最短路径问题的模型. 2.能运用几何模型解决问题.
教学内容
教学重点:会用最短路径的基本模型解决问题. 教学难点:探索发现“最短路径”的方案.
教学过程
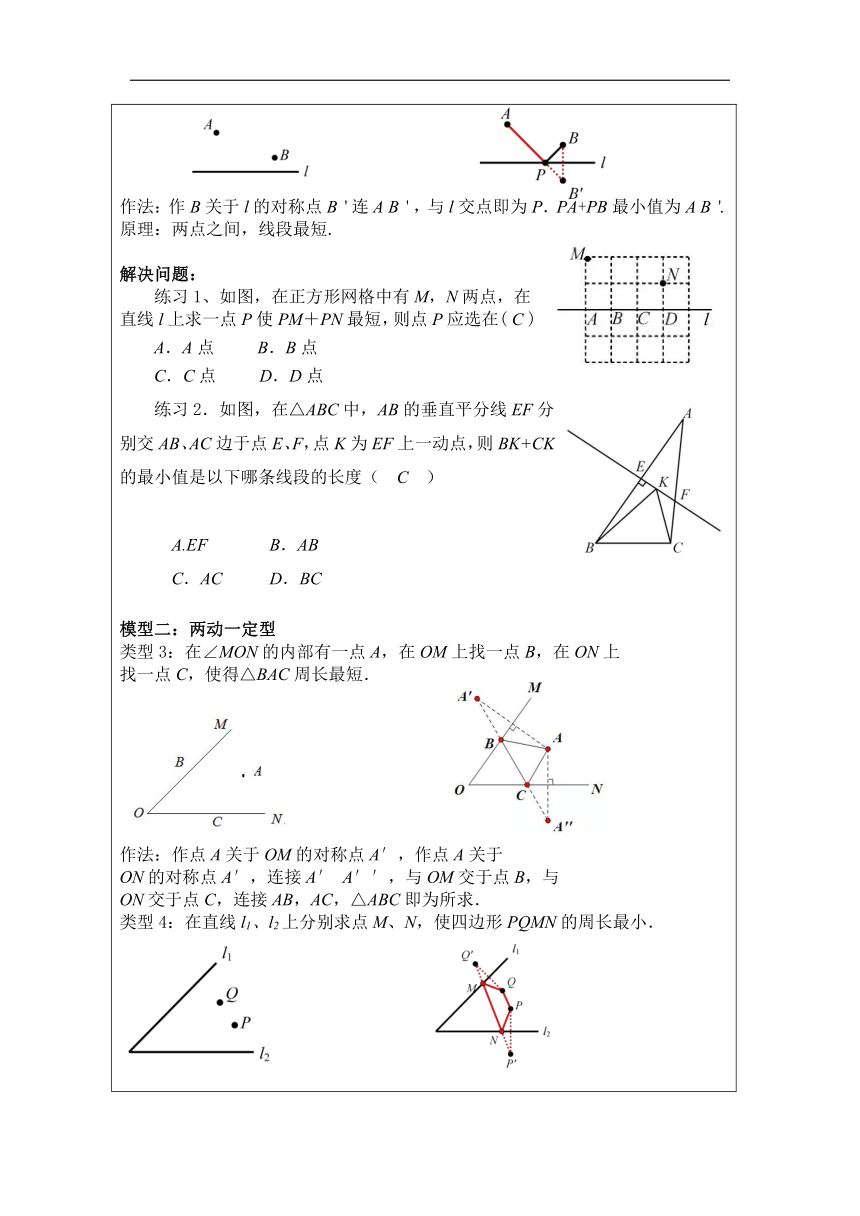
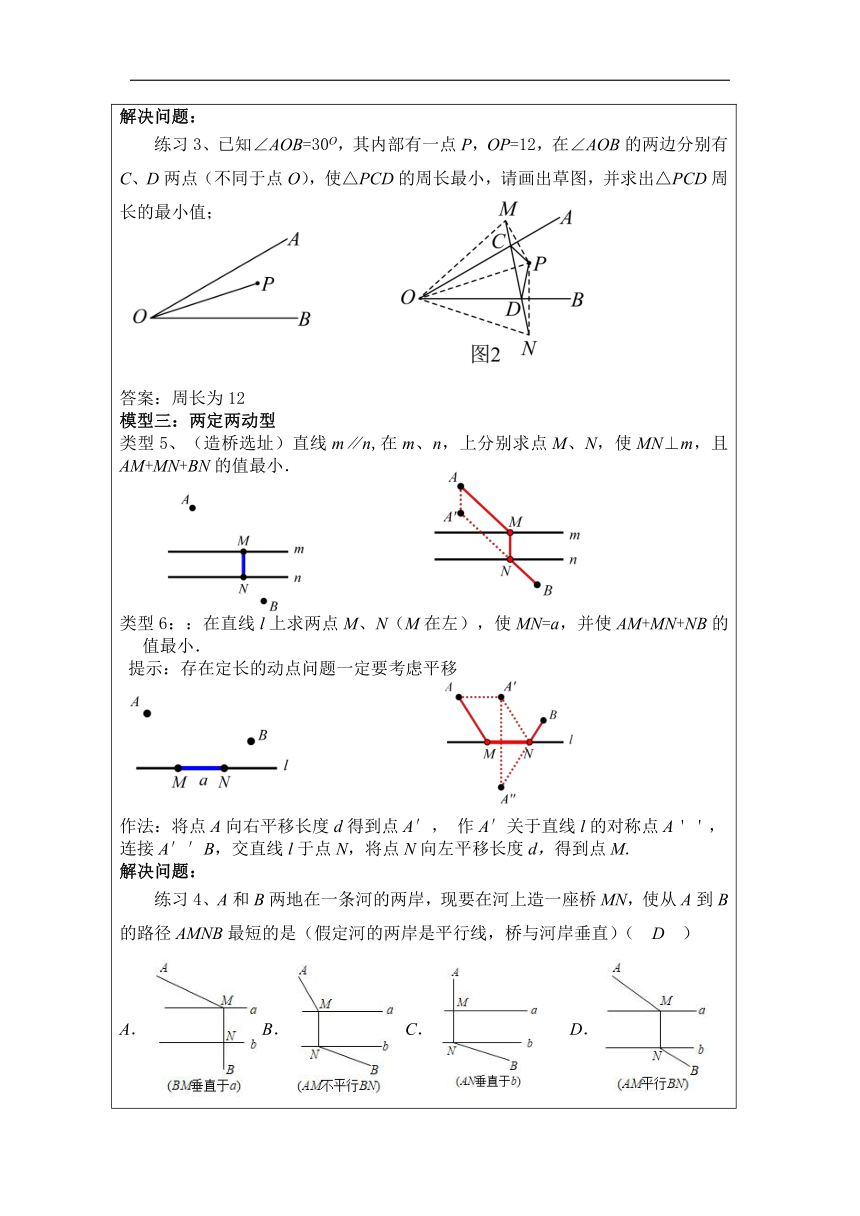
一、知识回顾. 1.在学习最短路径问题时,我们学习了哪两个经典问题? 将军饮马,造桥选址 2.最短路径问题主要应用了什么基础知识? 两点之间线段最短,垂线段最短;三角形三边关系;轴对称;平移. 二、模型归纳. 模型一:两定一动型 类型1:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB最小. 作法:连AB,与l交点即为P,PA+PB最小,且最小值等于AB. 原理:两点之间线段最短. 类型2:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB的和最小. 作法:作B关于l的对称点B'连A B',与l交点即为P.PA+PB最小值为A B'. 原理:两点之间,线段最短. 解决问题: 练习1、如图,在正方形网格中有M,N两点,在直线l上求一点P使PM+PN最短,则点P应选在( C ) A.A点 B.B点 C.C点 D.D点 练习2.如图,在△ABC中,AB的垂直平分线EF分别交AB、AC边于点E、F,点K为EF上一动点,则BK+CK的最小值是以下哪条线段的长度( C ) A.EF B.AB C.AC D.BC 模型二:两动一定型 类型3:在∠MON的内部有一点A,在OM上找一点B,在ON上 找一点C,使得△BAC周长最短. 作法:作点A关于OM的对称点A′,作点A关于 ON的对称点A′,连接A′ A′′,与OM交于点B,与 ON交于点C,连接AB,AC,△ABC即为所求. 类型4:在直线l1、l2上分别求点M、N,使四边形PQMN的周长最小. 解决问题: 练习3、已知∠AOB=30O,其内部有一点P,OP=12,在∠AOB的两边分别有C、D两点(不同于点O),使△PCD的周长最小,请画出草图,并求出△PCD周长的最小值; 答案:周长为12 模型三:两定两动型 类型5、(造桥选址)直线m∥n,在m、n,上分别求点M、N,使MN⊥m,且AM+MN+BN的值最小. 类型6::在直线l上求两点M、N(M在左),使MN=a,并使AM+MN+NB的值最小. 提示:存在定长的动点问题一定要考虑平移 作法:将点A向右平移长度d得到点A′, 作A′关于直线l的对称点A'',连接A′′B,交直线l于点N,将点N向左平移长度d,得到点M. 解决问题: 练习4、A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( D ) A.B.C. D. 模型四: 垂线段最短型 类型7:在l1上求点A,在l2上求点B,使PA+AB值最小. 类型8:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之差最小,即|PA-PB |最小. 作法:连接AB,作AB的中垂线与l的交点,即为所求点P 此时|PA-PB |=0 类型9:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之差最大,即|PA-PB |最大. 作法:作直线AB,与直线l的交点即为P,最大值=AB. 类型10:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之差最大,即|PA-PB|最大. 作法:作点B关于l的对称点B',连接AB',交l于点P即为所求,最大值为AB的长度. 解决问题: 练习5.如图,点E在等边△ABC的边BC上,BE=4,射线CD⊥BC,垂足为点C,点P是射线CD上一动点,点F是线段AB上一动点,当EP+FP的值最小时,BF=5,则AB的长为( A ) A.7 B.8 C.9 D.10 三、课后小结 这节课你学到了什么? 四、课后作业: 1.如图,∠AOB=60°,P是∠AOB角平分线上一点,PD⊥AO,垂足为D,点M是OP的中点,且DM=4,如果点C是射线OB上一个动点,则PC的最小值是( ) A.8 B.6 C.4 D.2 2.如图,等腰△ABC的底边BC=4,面积为8,腰AB的垂直平分线EF分别交AB、AC于点E、F,若D为边BC的中点,M为线段EF上一动点,则△BDM周长的最小值为多少?( B ) A.4 B.6 C.8 D.10 3.如图,在四边形ABCD中,∠C=αo,∠B=∠D=90o,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( D ) A.α B.2α C.180-α D.180-2α 4.如图,在△ABC中,AC=BC=10,∠ACB=4∠A,BD平分∠ABC交AC于点D,点E,F分别是线段BD,BC上的动点,则CE+EF的最小值是 5 .
课程基本信息
学科 数学 年级 八年级 学期 秋季
课题 最短路径问题
教科书 书 名:初中数学 出版社:人民教育出版社
教学目标
1.熟悉常见的解决最短路径问题的模型. 2.能运用几何模型解决问题.
教学内容
教学重点:会用最短路径的基本模型解决问题. 教学难点:探索发现“最短路径”的方案.
教学过程
一、知识回顾. 1.在学习最短路径问题时,我们学习了哪两个经典问题? 将军饮马,造桥选址 2.最短路径问题主要应用了什么基础知识? 两点之间线段最短,垂线段最短;三角形三边关系;轴对称;平移. 二、模型归纳. 模型一:两定一动型 类型1:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB最小. 作法:连AB,与l交点即为P,PA+PB最小,且最小值等于AB. 原理:两点之间线段最短. 类型2:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之和最小,即PA+PB的和最小. 作法:作B关于l的对称点B'连A B',与l交点即为P.PA+PB最小值为A B'. 原理:两点之间,线段最短. 解决问题: 练习1、如图,在正方形网格中有M,N两点,在直线l上求一点P使PM+PN最短,则点P应选在( C ) A.A点 B.B点 C.C点 D.D点 练习2.如图,在△ABC中,AB的垂直平分线EF分别交AB、AC边于点E、F,点K为EF上一动点,则BK+CK的最小值是以下哪条线段的长度( C ) A.EF B.AB C.AC D.BC 模型二:两动一定型 类型3:在∠MON的内部有一点A,在OM上找一点B,在ON上 找一点C,使得△BAC周长最短. 作法:作点A关于OM的对称点A′,作点A关于 ON的对称点A′,连接A′ A′′,与OM交于点B,与 ON交于点C,连接AB,AC,△ABC即为所求. 类型4:在直线l1、l2上分别求点M、N,使四边形PQMN的周长最小. 解决问题: 练习3、已知∠AOB=30O,其内部有一点P,OP=12,在∠AOB的两边分别有C、D两点(不同于点O),使△PCD的周长最小,请画出草图,并求出△PCD周长的最小值; 答案:周长为12 模型三:两定两动型 类型5、(造桥选址)直线m∥n,在m、n,上分别求点M、N,使MN⊥m,且AM+MN+BN的值最小. 类型6::在直线l上求两点M、N(M在左),使MN=a,并使AM+MN+NB的值最小. 提示:存在定长的动点问题一定要考虑平移 作法:将点A向右平移长度d得到点A′, 作A′关于直线l的对称点A'',连接A′′B,交直线l于点N,将点N向左平移长度d,得到点M. 解决问题: 练习4、A和B两地在一条河的两岸,现要在河上造一座桥MN,使从A到B的路径AMNB最短的是(假定河的两岸是平行线,桥与河岸垂直)( D ) A.B.C. D. 模型四: 垂线段最短型 类型7:在l1上求点A,在l2上求点B,使PA+AB值最小. 类型8:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之差最小,即|PA-PB |最小. 作法:连接AB,作AB的中垂线与l的交点,即为所求点P 此时|PA-PB |=0 类型9:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之差最大,即|PA-PB |最大. 作法:作直线AB,与直线l的交点即为P,最大值=AB. 类型10:在定直线l上找一个动点P,使动点P到两个定点A与B的距离之差最大,即|PA-PB|最大. 作法:作点B关于l的对称点B',连接AB',交l于点P即为所求,最大值为AB的长度. 解决问题: 练习5.如图,点E在等边△ABC的边BC上,BE=4,射线CD⊥BC,垂足为点C,点P是射线CD上一动点,点F是线段AB上一动点,当EP+FP的值最小时,BF=5,则AB的长为( A ) A.7 B.8 C.9 D.10 三、课后小结 这节课你学到了什么? 四、课后作业: 1.如图,∠AOB=60°,P是∠AOB角平分线上一点,PD⊥AO,垂足为D,点M是OP的中点,且DM=4,如果点C是射线OB上一个动点,则PC的最小值是( ) A.8 B.6 C.4 D.2 2.如图,等腰△ABC的底边BC=4,面积为8,腰AB的垂直平分线EF分别交AB、AC于点E、F,若D为边BC的中点,M为线段EF上一动点,则△BDM周长的最小值为多少?( B ) A.4 B.6 C.8 D.10 3.如图,在四边形ABCD中,∠C=αo,∠B=∠D=90o,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF的度数为( D ) A.α B.2α C.180-α D.180-2α 4.如图,在△ABC中,AC=BC=10,∠ACB=4∠A,BD平分∠ABC交AC于点D,点E,F分别是线段BD,BC上的动点,则CE+EF的最小值是 5 .
