10.5一次函数与一元一次不等式同步练习(含答案)青岛版数学八年级下册
文档属性
| 名称 | 10.5一次函数与一元一次不等式同步练习(含答案)青岛版数学八年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 646.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 00:00:00 | ||
图片预览


文档简介
10.5 一次函数与一元一次不等式
一、单选题
1.如图,已知直线过点,过点的直线交轴于点,则关于的不等式的解集为( )
A. B. C. D.
2.如图,一次函数的图像与一次函数(为常数,且)的图像相交于点 ,则关于,的方程组 的解是( )
A. B. C. D.
3.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
4.如图,直线()经过点,,则关于的不等式的解集为( )
A. B. C. D.
5.如图,在平面直角坐标系中,一次函数经过,两点,则不等式的解是
A. B. C. D.
6.已知直线与直线相交于点,那么关于x的方程的解为( )
A. B. C. D.
7.如图,一次函数y=ax+b的图象经过A、B两点,则关于x的不等式ax+b<0的解集是( )
A.x<﹣1 B.x<2 C.x>﹣1 D.x>2
8.一次函数和的图象如图所示,则方程组的解是( )
A. B. C. D.
9.如图,一次函数的图象经过点,则关于的不等式的解集是( )
A. B. C. D.
10.如图,直线交坐标轴于两点,则不等式的解集为( )
A. B. C. D.
二、填空题
11.一次函数与的图象如图,则下列结论:①;②;③关于的方程的解是;④当时,.则其中正确的序号有 .
12.一次函数(k、b为常数,且k≠0)的图象如图所示.根据图象信息可求得关于的方程的解为 .
13.如图,已知直线y=ax+b(a≠0)和双曲线y=(k≠0)相交于A.B两点,则根据图象可得,关于x,y的方程组的解是
14.如图,已知一次函数的图象为直线l,直线l过和,则关于x的方程的解为 .
15.如图,两条直线:和相交于点,则方程组的解是 .
16.如图,直线L1:y=x+b与直线L2:y=ax+相交于点P(1,2),则关于x的不等式x+b>ax+的解集为 .
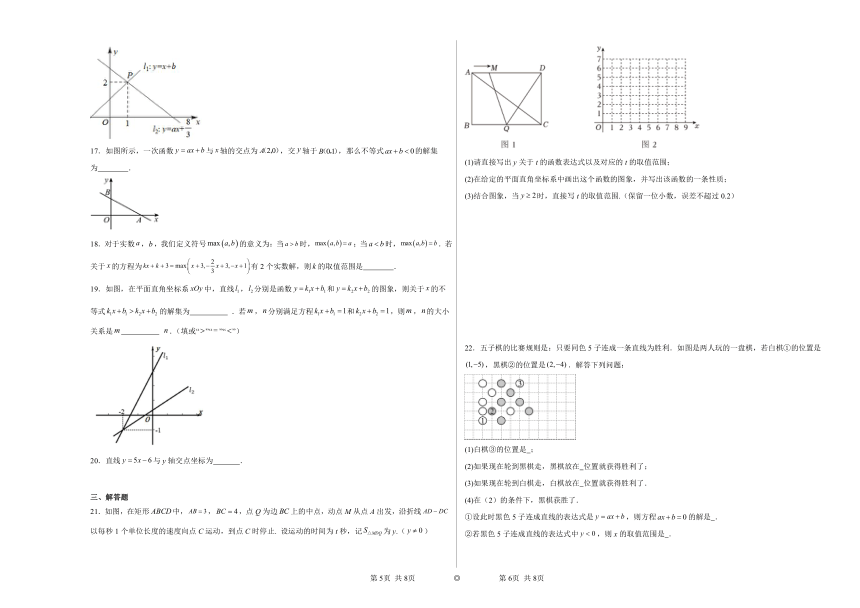
17.如图所示,一次函数与轴的交点为,交轴于,那么不等式的解集为 .
18.对于实数,,我们定义符号的意义为:当时,;当时,.若关于的方程为有2个实数解,则的取值范围是 .
19.如图,在平面直角坐标系中,直线,分别是函数和的图象,则关于的不等式的解集为 .若,分别满足方程和,则,的大小关系是 .(填或“”“”“”)
20.直线与y轴交点坐标为 .
三、解答题
21.如图,在矩形中,,,点Q为边上的中点,动点M从点A出发,沿折线以每秒1个单位长度的速度向点C运动,到点C时停止. 设运动的时间为t秒,记为y.()
(1)请直接写出y关于t的函数表达式以及对应的t的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合图象,当时,直接写t的取值范围.(保留一位小数,误差不超过0.2)
22.五子棋的比赛规则是:只要同色5子连成一条直线为胜利.如图是两人玩的一盘棋,若白棋①的位置是,黑棋②的位置是.解答下列问题:
(1)白棋③的位置是 ;
(2)如果现在轮到黑棋走,黑棋放在 位置就获得胜利了;
(3)如果现在轮到白棋走,白棋放在 位置就获得胜利了.
(4)在(2)的条件下,黑棋获胜了.
①设此时黑色5子连成直线的表达式是,则方程的解是 .
②若黑色5子连成直线的表达式中,则x的取值范围是 .
23.如图,在平面直角坐标系中,直线与直线相交与一点,在轴上的截距为4.
(1)直线,的表达式;
(2)讨论与的大小关系.
24.(1)在同一坐标系中画出函数和的图象;
(2)若两函数图象分别与x轴交于点A、B,求两函数图象与x轴围成的的面积.
25.临汾市某公园翻修后,推出了游船项目,为大众提供了一个可以玩桌游、商业等活动的场合.这个项目有甲、乙两种消费卡,已知甲、乙两种消费卡的费用y(元)与消费次数x(次)的函数关系如图所示.根据图中信息,解答下列问题:
(1)分别求出选择甲、乙两种消费卡y关于x的函数解析式;
(2)点B的坐标为______,点B表示的实际意义为____________.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
2.C
3.A
4.C
5.D
6.C
7.B
8.B
9.A
10.B
11.①③④
12.;
13.,或,
14.
15.
16.
17.
18.和或
19. x>-2; <
20.
21.(1)
(2)图象略,在范围内,随着的增大而增大;
(3)当时,或.
22.(1)
(2)或
(3)
(4)①或或或或或;②且x为正整数
23.(1):;:
(2)当时,,当时,,当时,.
24.(1)略;(2)
25.(1),
(2);当消费10次时,两种消费卡消费一样,都是200元
答案第1页,共2页
答案第1页,共2页
一、单选题
1.如图,已知直线过点,过点的直线交轴于点,则关于的不等式的解集为( )
A. B. C. D.
2.如图,一次函数的图像与一次函数(为常数,且)的图像相交于点 ,则关于,的方程组 的解是( )
A. B. C. D.
3.数形结合是解决数学问题常用的思想方法.如图,直线y=x+5和直线y=ax+b,相交于点P ,根据图象可知,方程x+5=ax+b的解是( )
A.x=20 B.x=5 C.x=25 D.x=15
4.如图,直线()经过点,,则关于的不等式的解集为( )
A. B. C. D.
5.如图,在平面直角坐标系中,一次函数经过,两点,则不等式的解是
A. B. C. D.
6.已知直线与直线相交于点,那么关于x的方程的解为( )
A. B. C. D.
7.如图,一次函数y=ax+b的图象经过A、B两点,则关于x的不等式ax+b<0的解集是( )
A.x<﹣1 B.x<2 C.x>﹣1 D.x>2
8.一次函数和的图象如图所示,则方程组的解是( )
A. B. C. D.
9.如图,一次函数的图象经过点,则关于的不等式的解集是( )
A. B. C. D.
10.如图,直线交坐标轴于两点,则不等式的解集为( )
A. B. C. D.
二、填空题
11.一次函数与的图象如图,则下列结论:①;②;③关于的方程的解是;④当时,.则其中正确的序号有 .
12.一次函数(k、b为常数,且k≠0)的图象如图所示.根据图象信息可求得关于的方程的解为 .
13.如图,已知直线y=ax+b(a≠0)和双曲线y=(k≠0)相交于A.B两点,则根据图象可得,关于x,y的方程组的解是
14.如图,已知一次函数的图象为直线l,直线l过和,则关于x的方程的解为 .
15.如图,两条直线:和相交于点,则方程组的解是 .
16.如图,直线L1:y=x+b与直线L2:y=ax+相交于点P(1,2),则关于x的不等式x+b>ax+的解集为 .
17.如图所示,一次函数与轴的交点为,交轴于,那么不等式的解集为 .
18.对于实数,,我们定义符号的意义为:当时,;当时,.若关于的方程为有2个实数解,则的取值范围是 .
19.如图,在平面直角坐标系中,直线,分别是函数和的图象,则关于的不等式的解集为 .若,分别满足方程和,则,的大小关系是 .(填或“”“”“”)
20.直线与y轴交点坐标为 .
三、解答题
21.如图,在矩形中,,,点Q为边上的中点,动点M从点A出发,沿折线以每秒1个单位长度的速度向点C运动,到点C时停止. 设运动的时间为t秒,记为y.()
(1)请直接写出y关于t的函数表达式以及对应的t的取值范围;
(2)在给定的平面直角坐标系中画出这个函数的图象,并写出该函数的一条性质;
(3)结合图象,当时,直接写t的取值范围.(保留一位小数,误差不超过0.2)
22.五子棋的比赛规则是:只要同色5子连成一条直线为胜利.如图是两人玩的一盘棋,若白棋①的位置是,黑棋②的位置是.解答下列问题:
(1)白棋③的位置是 ;
(2)如果现在轮到黑棋走,黑棋放在 位置就获得胜利了;
(3)如果现在轮到白棋走,白棋放在 位置就获得胜利了.
(4)在(2)的条件下,黑棋获胜了.
①设此时黑色5子连成直线的表达式是,则方程的解是 .
②若黑色5子连成直线的表达式中,则x的取值范围是 .
23.如图,在平面直角坐标系中,直线与直线相交与一点,在轴上的截距为4.
(1)直线,的表达式;
(2)讨论与的大小关系.
24.(1)在同一坐标系中画出函数和的图象;
(2)若两函数图象分别与x轴交于点A、B,求两函数图象与x轴围成的的面积.
25.临汾市某公园翻修后,推出了游船项目,为大众提供了一个可以玩桌游、商业等活动的场合.这个项目有甲、乙两种消费卡,已知甲、乙两种消费卡的费用y(元)与消费次数x(次)的函数关系如图所示.根据图中信息,解答下列问题:
(1)分别求出选择甲、乙两种消费卡y关于x的函数解析式;
(2)点B的坐标为______,点B表示的实际意义为____________.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.C
2.C
3.A
4.C
5.D
6.C
7.B
8.B
9.A
10.B
11.①③④
12.;
13.,或,
14.
15.
16.
17.
18.和或
19. x>-2; <
20.
21.(1)
(2)图象略,在范围内,随着的增大而增大;
(3)当时,或.
22.(1)
(2)或
(3)
(4)①或或或或或;②且x为正整数
23.(1):;:
(2)当时,,当时,,当时,.
24.(1)略;(2)
25.(1),
(2);当消费10次时,两种消费卡消费一样,都是200元
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
