北师大版数学八年级下册1.1等腰三角形同步练习(含答案)
文档属性
| 名称 | 北师大版数学八年级下册1.1等腰三角形同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 649.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 17:11:18 | ||
图片预览

文档简介
1.1 等腰三角形
一、单选题
1.若,则 以a、b为边长等腰三角形的周长为( )
A.19 B.22 C.23 D.19或23
2.在中,若,则是( )
A.不等边三角形 B.等边三角形 C.直角三角形 D.等腰三角形
3.在中,,,于点,若,则( )
A. B. C. D.
4.已知点的坐标为,点的坐标为,点为坐标轴上一点,若为等腰三角形,则这样的点有( )个
A.4 B.5 C.6 D.7
5.在中,,,点是线段上一动点,作射线,点关于的对称点为,直线与相交于点,连接,下面结论正确的个数是( )
①线段;②当时,四边形的面积是3;③随着点的移动,的角度不变;④当点运动到点时,线段为4;
A.1 B.2 C.3 D.42
6.如图,在一单位为1的方格纸上,,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若的顶点坐标分别为,,,则依图中所示规律,的坐标为( )
A. B. C. D.
7.如图,等腰△ABC,AB=AC,,ADBC于点D.点P是BA延长线上一点,O点是线段AD上一点,OP=OC,下面的结论:①AC平分∠PAD;②∠APO=∠DCO;③△OPC是等边三角形;④AC=AO+AP.其中正确结论的个数为( )
A.4 B.3 C.2 D.1
8.已知,如图在中,,以点B为圆心,为半径画弧,交于点,则线段的长为( )
A. B. C. D.
9.已知是直角边长为1的等腰直角三角形,以的斜边为直角边,画第一个等腰,再以的斜边为直角边,画第二个等腰,…,依此类推,则画出的第2023个等腰直角三角形的面积是( )
A. B. C. D.
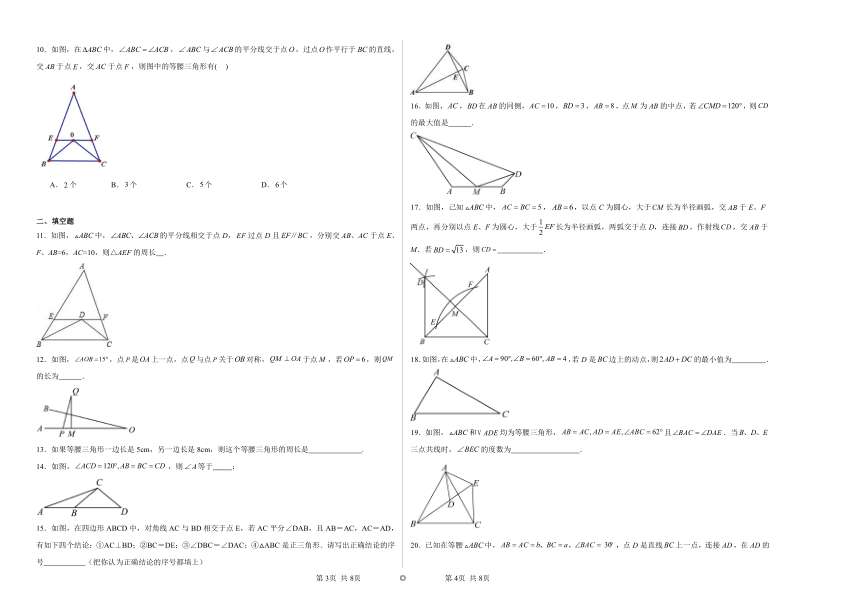
10.如图,在中,,与的平分线交于点,过点作平行于的直线,交于点,交于点,则图中的等腰三角形有( )
A.个 B.个 C.个 D.个
二、填空题
11.如图,中,的平分线相交于点D,过点D且,分别交AB、AC于点E、F、AB=6,AC=10,则△AEF的周长 .
12.如图,,点是上一点,点与点关于对称,于点,若,则的长为 .
13.如果等腰三角形一边长是5cm,另一边长是8cm,则这个等腰三角形的周长是 .
14.如图,,则等于 ;
15.如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.请写出正确结论的序号 (把你认为正确结论的序号都填上)
16.如图,,在的同侧,,,,点为的中点,若,则的最大值是 .
17.如图,己知中,,,以点C为圆心,大于长为半径画弧,交于E、F两点,再分别以点E、F为圆心,大于长为半径画弧,两弧交于点D,连接,作射线,交于M.若,则 .
18.如图,在中,,若D是边上的动点,则的最小值为 .
19.如图,和均为等腰三角形,且.当三点共线时,的度数为 .
20.已知在等腰中,,点D是直线上一点,连接,在AD的左侧做等腰,其中,连接,则的最小值的平方为 (用a、b表示).
三、解答题
21.为了缓解望城区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图). 从侧面 D 点测得显示牌顶端C点的仰角,测得显示牌底端B点的仰角 .
(1)已知立杆高度是,求路况显示牌的高度(即求的长度, 结果保留根号).
(2)已知路况显示牌最高点C距离地面9米(即米),求立杆高度(结果保留根号).
22.在学习了勾股定理之后,甲乙丙三位同学在方格图(正方形的边长都为1)中比赛找“整数三角形”,什么叫“整数三角形”呢?他们三人规定:边长和面积都是整数的三角形才能叫“整数三角形”.甲同学很快找到了如图1的“整数三角形”,一会儿后乙同学也找到了周长为24的“整数三角形”.丙同学受到甲、乙两同学的启发找到了两个不同的等腰“整数三角形”.请完成:
(1)以点A为一个顶点,在图2中作出乙同学找到的周长为24的“整数三角形”,并在每边周边标注其边长;
(2)在图3中作出两个不同的等腰“整数三角形”,并在每边周边标注其边长;
(3)你还能找到一个等边“整数三角形”吗?若能找出,请写出它的边长;若不能,请说明理由.
23.已知等腰三角形三边、、长分别为,,,求这个三角形的周长.
24.(1)如图1,已知,以为边分别向外作等腰直角三角形和等腰直角三角形,连接.猜想与有什么数量关系?并说明理由.
(2)在幸福村的休闲广场上种有四棵景观树,在如图2所示A、B、C、E的位置,数学兴趣小组的同学测得,米,米.
①求A、C两棵树之间的距离;(结果保留根号)
②如果,且,求B、E两棵树之间的距离.
25.【观察与发现】如图1,将长方形纸片沿短边的中点连线对折;展开后再将长方形沿直线折起,使得点落在上,对应点记为,连接.
(1)用尺规作图法作出折痕;
(2)可以发现的形状为 ,与的关系为 .
【思考与证明】如图2,改变折痕的位置,且 ,将下面的长方形沿对折后,点、的对应点分别为;展开后再将矩形沿直线折起,使得点落在,连接,判断与的关系否还成立?并说明理由.
【探索与创新】如图3,改变折痕的位置的同时,改变折痕的位置为,同样使得点落在上,对应点记为.点、的对应点分别为,连接 .判断形状,并说明与的数量关系.
【实践与应用】如图4,在给出的长方形纸片中,点为边上一点,连接,根据上面得到的结论,用折叠的方法即可以将三等分,请尝试画出折痕.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
2.D
3.C
4.D
5.C
6.D
7.B
8.C
9.A
10.C
11.16.
12.3
13.21或18
14.
15.①
16.
17.6
18.12
19./56度
20.
21.(1)路况显示牌的高度为 (2)立杆高度为
22.略
23.
24.(1),略;(2)米;(3)100米
25.(1)略;(2)等边三角形,;思考与证明:与的关系还成立,略;探索与创新:是等腰三角形;;实践与应用:略;
答案第1页,共2页
答案第1页,共2页
一、单选题
1.若,则 以a、b为边长等腰三角形的周长为( )
A.19 B.22 C.23 D.19或23
2.在中,若,则是( )
A.不等边三角形 B.等边三角形 C.直角三角形 D.等腰三角形
3.在中,,,于点,若,则( )
A. B. C. D.
4.已知点的坐标为,点的坐标为,点为坐标轴上一点,若为等腰三角形,则这样的点有( )个
A.4 B.5 C.6 D.7
5.在中,,,点是线段上一动点,作射线,点关于的对称点为,直线与相交于点,连接,下面结论正确的个数是( )
①线段;②当时,四边形的面积是3;③随着点的移动,的角度不变;④当点运动到点时,线段为4;
A.1 B.2 C.3 D.42
6.如图,在一单位为1的方格纸上,,都是斜边在x轴上,斜边长分别为2,4,6,…的等腰直角三角形,若的顶点坐标分别为,,,则依图中所示规律,的坐标为( )
A. B. C. D.
7.如图,等腰△ABC,AB=AC,,ADBC于点D.点P是BA延长线上一点,O点是线段AD上一点,OP=OC,下面的结论:①AC平分∠PAD;②∠APO=∠DCO;③△OPC是等边三角形;④AC=AO+AP.其中正确结论的个数为( )
A.4 B.3 C.2 D.1
8.已知,如图在中,,以点B为圆心,为半径画弧,交于点,则线段的长为( )
A. B. C. D.
9.已知是直角边长为1的等腰直角三角形,以的斜边为直角边,画第一个等腰,再以的斜边为直角边,画第二个等腰,…,依此类推,则画出的第2023个等腰直角三角形的面积是( )
A. B. C. D.
10.如图,在中,,与的平分线交于点,过点作平行于的直线,交于点,交于点,则图中的等腰三角形有( )
A.个 B.个 C.个 D.个
二、填空题
11.如图,中,的平分线相交于点D,过点D且,分别交AB、AC于点E、F、AB=6,AC=10,则△AEF的周长 .
12.如图,,点是上一点,点与点关于对称,于点,若,则的长为 .
13.如果等腰三角形一边长是5cm,另一边长是8cm,则这个等腰三角形的周长是 .
14.如图,,则等于 ;
15.如图,在四边形ABCD中,对角线AC与BD相交于点E,若AC平分∠DAB,且AB=AC,AC=AD,有如下四个结论:①AC⊥BD;②BC=DE;③∠DBC=∠DAC;④△ABC是正三角形.请写出正确结论的序号 (把你认为正确结论的序号都填上)
16.如图,,在的同侧,,,,点为的中点,若,则的最大值是 .
17.如图,己知中,,,以点C为圆心,大于长为半径画弧,交于E、F两点,再分别以点E、F为圆心,大于长为半径画弧,两弧交于点D,连接,作射线,交于M.若,则 .
18.如图,在中,,若D是边上的动点,则的最小值为 .
19.如图,和均为等腰三角形,且.当三点共线时,的度数为 .
20.已知在等腰中,,点D是直线上一点,连接,在AD的左侧做等腰,其中,连接,则的最小值的平方为 (用a、b表示).
三、解答题
21.为了缓解望城区内一些主要路段交通拥挤的现状,交警队在一些主要路口设立了交通路况显示牌(如图). 从侧面 D 点测得显示牌顶端C点的仰角,测得显示牌底端B点的仰角 .
(1)已知立杆高度是,求路况显示牌的高度(即求的长度, 结果保留根号).
(2)已知路况显示牌最高点C距离地面9米(即米),求立杆高度(结果保留根号).
22.在学习了勾股定理之后,甲乙丙三位同学在方格图(正方形的边长都为1)中比赛找“整数三角形”,什么叫“整数三角形”呢?他们三人规定:边长和面积都是整数的三角形才能叫“整数三角形”.甲同学很快找到了如图1的“整数三角形”,一会儿后乙同学也找到了周长为24的“整数三角形”.丙同学受到甲、乙两同学的启发找到了两个不同的等腰“整数三角形”.请完成:
(1)以点A为一个顶点,在图2中作出乙同学找到的周长为24的“整数三角形”,并在每边周边标注其边长;
(2)在图3中作出两个不同的等腰“整数三角形”,并在每边周边标注其边长;
(3)你还能找到一个等边“整数三角形”吗?若能找出,请写出它的边长;若不能,请说明理由.
23.已知等腰三角形三边、、长分别为,,,求这个三角形的周长.
24.(1)如图1,已知,以为边分别向外作等腰直角三角形和等腰直角三角形,连接.猜想与有什么数量关系?并说明理由.
(2)在幸福村的休闲广场上种有四棵景观树,在如图2所示A、B、C、E的位置,数学兴趣小组的同学测得,米,米.
①求A、C两棵树之间的距离;(结果保留根号)
②如果,且,求B、E两棵树之间的距离.
25.【观察与发现】如图1,将长方形纸片沿短边的中点连线对折;展开后再将长方形沿直线折起,使得点落在上,对应点记为,连接.
(1)用尺规作图法作出折痕;
(2)可以发现的形状为 ,与的关系为 .
【思考与证明】如图2,改变折痕的位置,且 ,将下面的长方形沿对折后,点、的对应点分别为;展开后再将矩形沿直线折起,使得点落在,连接,判断与的关系否还成立?并说明理由.
【探索与创新】如图3,改变折痕的位置的同时,改变折痕的位置为,同样使得点落在上,对应点记为.点、的对应点分别为,连接 .判断形状,并说明与的数量关系.
【实践与应用】如图4,在给出的长方形纸片中,点为边上一点,连接,根据上面得到的结论,用折叠的方法即可以将三等分,请尝试画出折痕.
第1页 共4页 ◎ 第2页 共4页
第1页 共4页 ◎ 第2页 共4页
参考答案:
1.D
2.D
3.C
4.D
5.C
6.D
7.B
8.C
9.A
10.C
11.16.
12.3
13.21或18
14.
15.①
16.
17.6
18.12
19./56度
20.
21.(1)路况显示牌的高度为 (2)立杆高度为
22.略
23.
24.(1),略;(2)米;(3)100米
25.(1)略;(2)等边三角形,;思考与证明:与的关系还成立,略;探索与创新:是等腰三角形;;实践与应用:略;
答案第1页,共2页
答案第1页,共2页
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
