人教版七年级数学下册9.1.1不等式及其解集课件(第1课时)(25张PPT)
文档属性
| 名称 | 人教版七年级数学下册9.1.1不等式及其解集课件(第1课时)(25张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 51.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 19:17:14 | ||
图片预览






文档简介
(共25张PPT)
第 1 课时 | 不等式及其解集
第九单元 不等式与不等式组
任 课 教 师 | X X X
人教版七年级数学下册
知识无涯,进步无界!
新理念
新模式
新课标
新征程
学习目标
1. 了解不等式及其解的概念,学会用不等式表示数量关系;
2. 理解不等式的解集;
3. 会在数轴上表示不等式的解集.
生活中的不等关系
160cm
162cm
不相等重量的物体
不相等的两位同学的身高
不相等的长度
长度不一的铅笔
160cm
162cm
162 > 160 或 160 < 162
思考:
对于不等关系的问题,我们如何用式子来表示它们呢?
情境1
一辆匀速行驶的汽车在11:20距离A地50km,要在12:00之前驶过A地,车速应满足什么条件?
情境2
设车速是x km/h
(1)从时间上看
(2)从路程上看
一辆匀速行驶的汽车在11:20距离A地50km,要在12:00之前驶过A地,车速应满足什么条件?
情境1
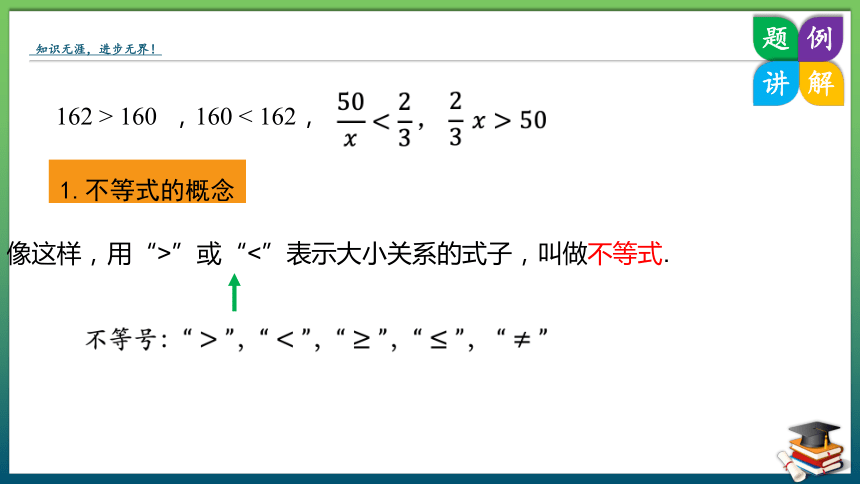
162 > 160 ,160 < 162,
像这样,用“>”或“<”表示大小关系的式子,叫做不等式.
1.不等式的概念
例1 判断下列式子是不是不等式:
(1) x≠5; (2) x+2 ≥ y+5 ;
(3) x-5y<0; (4) a=3 ;
(5)-3>0; (6) m2+n.
(1) x≠5; (2) x+2 ≥ y+5 ;
(3) x-5y<0; (4) a=3 ;
(5) m2+n ; (6) -3>0.
等式
代数式
例1 判断下列式子是不是不等式:
例2 用不等式表示下列数量关系:
(1)a是正数
(2)a与2的差是非负数
(3)x的4倍不大于1
(1)a是正数
(2)a与2的差是非负数
(3)x的4倍不大于1
例2 用不等式表示下列数量关系:
-1,0.1,3,9,10,100
问题1
2.不等式的解
使不等式成立的未知数的值,叫做不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
-1,0.1,3,9,10,100
问题1
问题2
无数个
3.不等式的解集
一般地,一个含有未知数的不等式的所有的解,
组成这个不等式的解集.
问题2
3.不等式的解集
一般地,一个含有未知数的不等式的所有的解,
组成这个不等式的解集.
求不等式的解集的过程叫做解不等式.
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
某个解是解集中的具体的值
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
例3 判断下列说法是否正确:
(1)x=1是x+3<7的解;
(3)x=10是不等式x+3>5的解集;
例3 判断下列说法是否正确:
(1)x=1是x+3<7的解;
(3)x=10是不等式x+3>5的解集;
代入:当x=1时,1+3<7成立
一个解
在数轴上表示解集
思考
0
1
2
3
4
5
6
-1
(1)先在数轴上找到表示2的点
(2)“大于”向右画
(3)把表示2 的点画成空心圆圈,表示解集不包括2.
练习
在数轴上表示下列不等式的解集
练习
在数轴上表示下列不等式的解集
练习
在数轴上表示下列不等式的解集
有等号(≥,≤)画实心点,无等号(>,<)画空心圈
大于向右画,小于向左画
小结
不等式的概念
不等式的解和解集
在数轴上表示不等式的解集
学
本课结束 感谢聆听!
第 1 课时 | 不等式及其解集
第九单元 不等式与不等式组
任 课 教 师 | X X X
人教版七年级数学下册
知识无涯,进步无界!
新理念
新模式
新课标
新征程
学习目标
1. 了解不等式及其解的概念,学会用不等式表示数量关系;
2. 理解不等式的解集;
3. 会在数轴上表示不等式的解集.
生活中的不等关系
160cm
162cm
不相等重量的物体
不相等的两位同学的身高
不相等的长度
长度不一的铅笔
160cm
162cm
162 > 160 或 160 < 162
思考:
对于不等关系的问题,我们如何用式子来表示它们呢?
情境1
一辆匀速行驶的汽车在11:20距离A地50km,要在12:00之前驶过A地,车速应满足什么条件?
情境2
设车速是x km/h
(1)从时间上看
(2)从路程上看
一辆匀速行驶的汽车在11:20距离A地50km,要在12:00之前驶过A地,车速应满足什么条件?
情境1
162 > 160 ,160 < 162,
像这样,用“>”或“<”表示大小关系的式子,叫做不等式.
1.不等式的概念
例1 判断下列式子是不是不等式:
(1) x≠5; (2) x+2 ≥ y+5 ;
(3) x-5y<0; (4) a=3 ;
(5)-3>0; (6) m2+n.
(1) x≠5; (2) x+2 ≥ y+5 ;
(3) x-5y<0; (4) a=3 ;
(5) m2+n ; (6) -3>0.
等式
代数式
例1 判断下列式子是不是不等式:
例2 用不等式表示下列数量关系:
(1)a是正数
(2)a与2的差是非负数
(3)x的4倍不大于1
(1)a是正数
(2)a与2的差是非负数
(3)x的4倍不大于1
例2 用不等式表示下列数量关系:
-1,0.1,3,9,10,100
问题1
2.不等式的解
使不等式成立的未知数的值,叫做不等式的解.
代入法是检验某个值是否是不等式的解的简单、实用的方法.
-1,0.1,3,9,10,100
问题1
问题2
无数个
3.不等式的解集
一般地,一个含有未知数的不等式的所有的解,
组成这个不等式的解集.
问题2
3.不等式的解集
一般地,一个含有未知数的不等式的所有的解,
组成这个不等式的解集.
求不等式的解集的过程叫做解不等式.
不等式的解 不等式的解集
区别 定义
特点
形式
联系
满足一个不等式的未知数的某个值
满足一个不等式的未知数的所有值
个体
全体
某个解是解集中的具体的值
解集一定包括了某个解
不等式的解与不等式的解集的区别与联系
例3 判断下列说法是否正确:
(1)x=1是x+3<7的解;
(3)x=10是不等式x+3>5的解集;
例3 判断下列说法是否正确:
(1)x=1是x+3<7的解;
(3)x=10是不等式x+3>5的解集;
代入:当x=1时,1+3<7成立
一个解
在数轴上表示解集
思考
0
1
2
3
4
5
6
-1
(1)先在数轴上找到表示2的点
(2)“大于”向右画
(3)把表示2 的点画成空心圆圈,表示解集不包括2.
练习
在数轴上表示下列不等式的解集
练习
在数轴上表示下列不等式的解集
练习
在数轴上表示下列不等式的解集
有等号(≥,≤)画实心点,无等号(>,<)画空心圈
大于向右画,小于向左画
小结
不等式的概念
不等式的解和解集
在数轴上表示不等式的解集
学
本课结束 感谢聆听!
