数学探究 杨辉三角的性质与应用 课件(共35张PPT)
文档属性
| 名称 | 数学探究 杨辉三角的性质与应用 课件(共35张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 33.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 00:00:00 | ||
图片预览








文档简介
(共35张PPT)
数学探究 杨辉三角的性质与应用
单击此处添加副标题
历史探源
帕斯卡 (B.Pascal,1623--1662)
杨辉三角(1261年)
杨辉三角具有独特的魅力和丰富的性质,中西方的众多数学家都曾研究和运用它,印度数学家称它为“须弥山之梯”,在伊朗,它是“海亚姆三角”,意大利人称之为“塔塔利亚三角形”…
今天,让我们一起走进它,探究它吧!
历史探源
数学探究过程:
观察和实验
归纳和猜想
推理和论证
请同学们仔细观察下面这个杨辉三角,你能从中发现哪些规律呢?
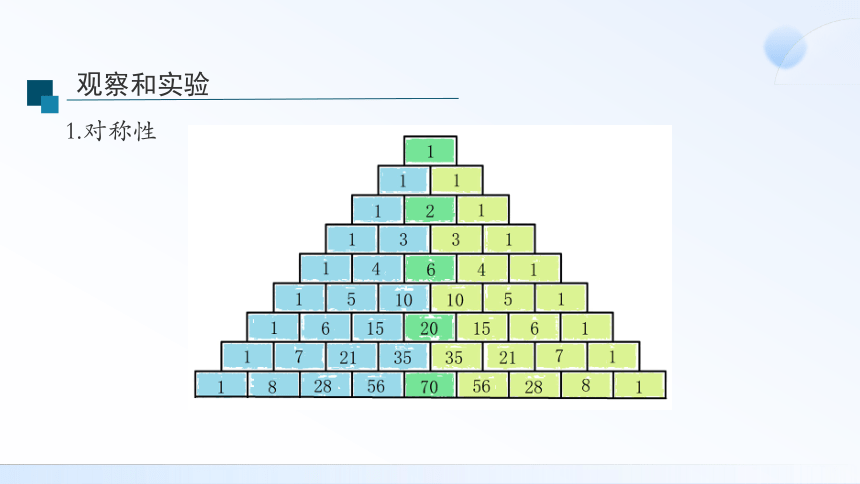
观察和实验
1.对称性
观察和实验
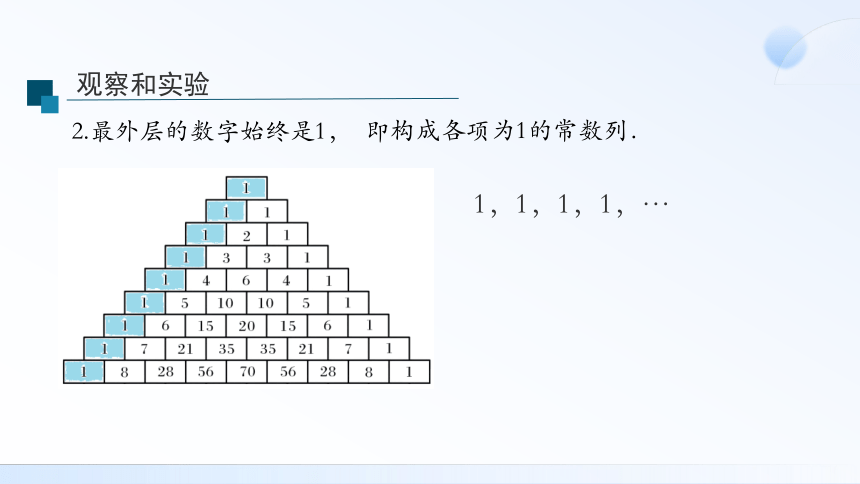
2.最外层的数字始终是1,
即构成各项为1的常数列.
观察和实验
1,1,1,1,…
3.第二层是从1开始的自然数,
观察和实验
1,2,3,4,…
即首项与公差都为1的等差数列.
2阶等差数列
观察和实验
1, 3, 6, 10, 15, 21,…
2 3 4 5 6 …
1 1 1 1 …
4.第三层为三角形数数列,
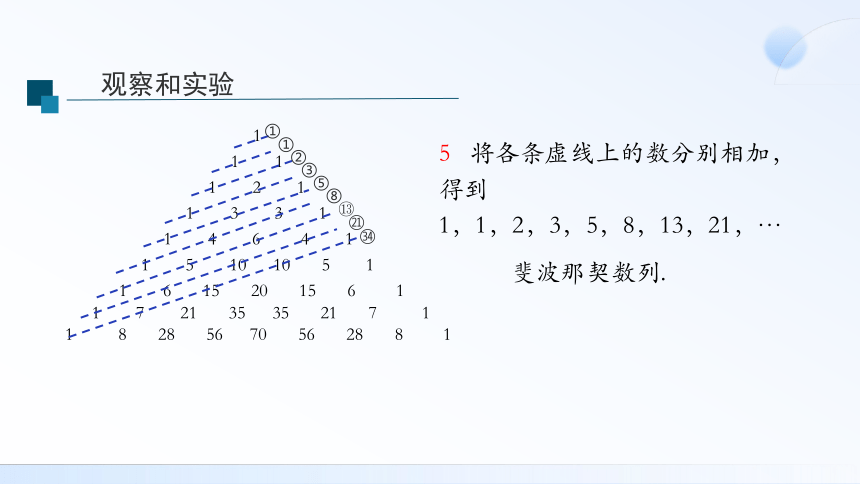
5 将各条虚线上的数分别相加,得到
1,1,2,3,5,8,13,21,…
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
①
①
②
③
⑤
⑧
观察和实验
斐波那契数列.
观察和实验
第 0 行
第 1 行
第 2 行
第 3 行
第 4 行
第 5 行
第 6 行
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
第 0 行
第 1 行
第 2 行
第 3 行
第 4 行
第 5 行
第 6 行
第n-1行
第 n 行
第n行就是 的展开式的二项式系数,第n行的第r个数可以表示为 .
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
观察和实验
归纳和猜想
杨辉三角第 8 行
1 8 28 56 70 56 28 8 1
第 10 行,第5个数
即120
直接写出杨辉三角的任意行、任意位置的数!
杨辉三角第 行,第 个数
杨辉三角第n行,第r+1个数
12 7
反过来,
数
形
请同学们继续观察每一行、相邻两行、斜行等,画一画,连一连,算一算,你还能发现哪些结论呢?
归纳和猜想
2=1+1
3=1+2
4=1+3
6=3+3
归纳和猜想
猜想1 除了最外层1以外,其余的数都等于它肩上的两个数相加,即
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
第 0 行
第 1 行
第 2 行
第 3 行
第 4 行
第 5 行
第 6 行
第n-1行
第 n 行
归纳和猜想
猜想2 第n行奇数项之和与偶数项之和相等,即
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1+6+1=4+4
1+10+5=5+10+1
归纳和猜想
猜想3 第n行各数平方和等于第2n行中间的数,即
1
1 1
12 + 22 + 12=6
12 + 32 + 32 + 12=20
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
第 0 行
第 1 行
第 2 行
第 3 行
第 4 行
第 5 行
第 6 行
归纳和猜想
猜想4 自腰上的某个1开始平行于腰的一条线上的连续n个数的和等于最后一个数斜右下方的那个数,即
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1+2+3+4=10
1+3+6+10=20
归纳和猜想
除了最外层1以外,其余的数都等于它肩上的两个数相加,即
递归性
证明:
猜想1
性质1
推理和论证
实际背景
从 这n个元素中取出r个元素的组合(共 个)可以分为两类,第一类含有某个元素 (共 个),第二类不含这个元素 (共 个).根据分类加法计数原理,等式成立.
推理和论证
自腰上的某个1开始平行于腰的一条线上的连续n个数的和等于最后一个数斜右下方的那个数,即
猜想4
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
推理和论证
证明:
猜想4
性质4
性质1
推理和论证
杨辉在《详解九章算法》中就记载有这样一道题目:“三角垛,下广,一面一十二个,上尖,问:计几何?”
题目大意: “有一个三角垛,最底层每条边上有12个圆球,最上层只有1个(上尖),问:总共有多少个圆球?”
应用: 1.堆垛问题:
一层 1 1
二层 1+2 3
三层 1+2+3 6
十二层 1+2+…+12 78
应用: 1.堆垛问题:
性质4 自腰上的某个1开始平行于腰的一条线上的连续n个数的和等于最后一个数斜右下方的那个数.
应用: 1.堆垛问题:
求n层三角垛的圆球总个数:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
应用: 1.堆垛问题:
答曰:三百六十四个.
术曰:下广加一乘之,平积,下广加二乘之,立高方积,如六而一,本法.
垛积术
大意:
应用: 1.堆垛问题:
“垛积术”源于古人对堆积成各种不同形状“垛”的物品,如酒坛、圆球、棋子等数量的计算;
茭草垛
四隅垛
三角垛
“化垛为数,以数表形”体现了古人高超的直观想象与逻辑推理素养!
应用: 1.堆垛问题:
开方古算题(杨辉《详解九章算法》):
积一百三十三万六千三百三十六尺,问为三乘方几何?
我国古代称平方为自乘,立方为再自乘,四次方为三乘方,因此,本题相当于解方程: .
应用: 2.开方问题:
“左袤乃积数,右袤乃隅算,中藏者皆廉,以廉乘商方,命实而除之”
请同学们查阅相关书籍或上网搜索相关资料,探究一下开方算法的具体操作及其中蕴含的算法思想,感受我国古代数学的独特风格。
应用: 2.开方问题:
课堂小结:
通过今天的学习,同学们有了哪些收获呢?
杨辉三角
杨辉三角的性质
杨辉三角的应用
发现问题
提出问题
分析问题
解决问题
杨辉三角的历史
课后探究活动要求:
以独立探究和小组合作相结合的方式开展探究活动.建议按如下步骤完成:
1.小组集体讨论探究方案,确定研究思路.
2.小组成员各自开展独立研究,并以专题作业的形式撰写研究报告.
3.小组内进行交流讨论,完善研究成果,并形成一份小组研究报告.
4.全班进行成果交流、评价.
研究报告的参考形式
杨辉三角的性质与应用
年级 班 完成时间:
1.课题组成员及分工
2.发现的数学结论及发现过程概述
3.证明思路及其形成过程描述
4.结论的证明或否定
5.杨辉三角的应用举例
6.收获与体会
数学探究 杨辉三角的性质与应用
单击此处添加副标题
历史探源
帕斯卡 (B.Pascal,1623--1662)
杨辉三角(1261年)
杨辉三角具有独特的魅力和丰富的性质,中西方的众多数学家都曾研究和运用它,印度数学家称它为“须弥山之梯”,在伊朗,它是“海亚姆三角”,意大利人称之为“塔塔利亚三角形”…
今天,让我们一起走进它,探究它吧!
历史探源
数学探究过程:
观察和实验
归纳和猜想
推理和论证
请同学们仔细观察下面这个杨辉三角,你能从中发现哪些规律呢?
观察和实验
1.对称性
观察和实验
2.最外层的数字始终是1,
即构成各项为1的常数列.
观察和实验
1,1,1,1,…
3.第二层是从1开始的自然数,
观察和实验
1,2,3,4,…
即首项与公差都为1的等差数列.
2阶等差数列
观察和实验
1, 3, 6, 10, 15, 21,…
2 3 4 5 6 …
1 1 1 1 …
4.第三层为三角形数数列,
5 将各条虚线上的数分别相加,得到
1,1,2,3,5,8,13,21,…
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1 7 21 35 35 21 7 1
1 8 28 56 70 56 28 8 1
①
①
②
③
⑤
⑧
观察和实验
斐波那契数列.
观察和实验
第 0 行
第 1 行
第 2 行
第 3 行
第 4 行
第 5 行
第 6 行
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
第 0 行
第 1 行
第 2 行
第 3 行
第 4 行
第 5 行
第 6 行
第n-1行
第 n 行
第n行就是 的展开式的二项式系数,第n行的第r个数可以表示为 .
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
观察和实验
归纳和猜想
杨辉三角第 8 行
1 8 28 56 70 56 28 8 1
第 10 行,第5个数
即120
直接写出杨辉三角的任意行、任意位置的数!
杨辉三角第 行,第 个数
杨辉三角第n行,第r+1个数
12 7
反过来,
数
形
请同学们继续观察每一行、相邻两行、斜行等,画一画,连一连,算一算,你还能发现哪些结论呢?
归纳和猜想
2=1+1
3=1+2
4=1+3
6=3+3
归纳和猜想
猜想1 除了最外层1以外,其余的数都等于它肩上的两个数相加,即
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
第 0 行
第 1 行
第 2 行
第 3 行
第 4 行
第 5 行
第 6 行
第n-1行
第 n 行
归纳和猜想
猜想2 第n行奇数项之和与偶数项之和相等,即
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1+6+1=4+4
1+10+5=5+10+1
归纳和猜想
猜想3 第n行各数平方和等于第2n行中间的数,即
1
1 1
12 + 22 + 12=6
12 + 32 + 32 + 12=20
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
第 0 行
第 1 行
第 2 行
第 3 行
第 4 行
第 5 行
第 6 行
归纳和猜想
猜想4 自腰上的某个1开始平行于腰的一条线上的连续n个数的和等于最后一个数斜右下方的那个数,即
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
1+2+3+4=10
1+3+6+10=20
归纳和猜想
除了最外层1以外,其余的数都等于它肩上的两个数相加,即
递归性
证明:
猜想1
性质1
推理和论证
实际背景
从 这n个元素中取出r个元素的组合(共 个)可以分为两类,第一类含有某个元素 (共 个),第二类不含这个元素 (共 个).根据分类加法计数原理,等式成立.
推理和论证
自腰上的某个1开始平行于腰的一条线上的连续n个数的和等于最后一个数斜右下方的那个数,即
猜想4
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
推理和论证
证明:
猜想4
性质4
性质1
推理和论证
杨辉在《详解九章算法》中就记载有这样一道题目:“三角垛,下广,一面一十二个,上尖,问:计几何?”
题目大意: “有一个三角垛,最底层每条边上有12个圆球,最上层只有1个(上尖),问:总共有多少个圆球?”
应用: 1.堆垛问题:
一层 1 1
二层 1+2 3
三层 1+2+3 6
十二层 1+2+…+12 78
应用: 1.堆垛问题:
性质4 自腰上的某个1开始平行于腰的一条线上的连续n个数的和等于最后一个数斜右下方的那个数.
应用: 1.堆垛问题:
求n层三角垛的圆球总个数:
1
1 1
1 2 1
1 3 3 1
1 4 6 4 1
1 5 10 10 5 1
1 6 15 20 15 6 1
应用: 1.堆垛问题:
答曰:三百六十四个.
术曰:下广加一乘之,平积,下广加二乘之,立高方积,如六而一,本法.
垛积术
大意:
应用: 1.堆垛问题:
“垛积术”源于古人对堆积成各种不同形状“垛”的物品,如酒坛、圆球、棋子等数量的计算;
茭草垛
四隅垛
三角垛
“化垛为数,以数表形”体现了古人高超的直观想象与逻辑推理素养!
应用: 1.堆垛问题:
开方古算题(杨辉《详解九章算法》):
积一百三十三万六千三百三十六尺,问为三乘方几何?
我国古代称平方为自乘,立方为再自乘,四次方为三乘方,因此,本题相当于解方程: .
应用: 2.开方问题:
“左袤乃积数,右袤乃隅算,中藏者皆廉,以廉乘商方,命实而除之”
请同学们查阅相关书籍或上网搜索相关资料,探究一下开方算法的具体操作及其中蕴含的算法思想,感受我国古代数学的独特风格。
应用: 2.开方问题:
课堂小结:
通过今天的学习,同学们有了哪些收获呢?
杨辉三角
杨辉三角的性质
杨辉三角的应用
发现问题
提出问题
分析问题
解决问题
杨辉三角的历史
课后探究活动要求:
以独立探究和小组合作相结合的方式开展探究活动.建议按如下步骤完成:
1.小组集体讨论探究方案,确定研究思路.
2.小组成员各自开展独立研究,并以专题作业的形式撰写研究报告.
3.小组内进行交流讨论,完善研究成果,并形成一份小组研究报告.
4.全班进行成果交流、评价.
研究报告的参考形式
杨辉三角的性质与应用
年级 班 完成时间:
1.课题组成员及分工
2.发现的数学结论及发现过程概述
3.证明思路及其形成过程描述
4.结论的证明或否定
5.杨辉三角的应用举例
6.收获与体会
