【沪科版七上同步练习】 第二章 整式加减(能力提升)检测题(含答案)
文档属性
| 名称 | 【沪科版七上同步练习】 第二章 整式加减(能力提升)检测题(含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 15.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2024-06-14 17:18:23 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【沪科版七上同步练习】
第二章整式加减(能力提升)检测题
一、单选题
1.下列计算正确的是( )
A.3a+2b=5ab B.3a 2a=6a2
C.(2m2)3=6m5 D.a6÷a2=a3
2.若与是同类项,则等于( )
A. B. C. D.
3.下列单项式中,能够与合并的是( )
A. B. C. D.
4.设,,则M与N的大小关系为( )
A. B. C. D.不能确定
5.对于任意的正数a,b,定义运算★,,计算的结果为( )
A. B. C.2 D.
二、填空题
6.若代数式3a4b 与0.2b a4和仍然是单项式,则x的值是 .
7.在式子中,单项式有 个.
8.若单项式与单项式的和仍是一个单项式,则的值是 .
9.在如图所示的平面直角坐标系中,是边长为的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是 .
10.在草稿纸上计算:① ;② ;③ ;④ ,观察你计算的结果,用你发现的规律直接写出下面式子的值 = .
11.规定:,,例如,,下列结论中,正确的是 (填写序号)
①若,则; ②若,则;
③能使成立的x的值不存在;④式子的最小值是5.
三、计算题
12.
(1)计算:
(2)化简:
13.计算:
(1)(-3)2.
(2)1.53.
(3)
(4)(-1)11.
14.已知-xm-2nym+n与-3x5y6的和是单项式,求 -5 -2 +(m+n)的值.
四、解答题
15.下列各组中的两项是不是同类项?为什么?
(1)2a2b与2ab2.
(2)3xy与yx.
(3)-2.1与
(4)2a与2ab.
16.如图,一块原边长分别为,的矩形,现将原矩形一边增加,另一边减少,变化后的面积为或.
(1) ; ; ;用含,的式子表示
(2)当时,变化后的面积会 ;增加或减少
(3)当时,有两种方案,第一种方案如图,第二种方案如图请你比较这两种方案,确定哪一种方案变化后的面积比较大.
17.定义:平面直角坐标系中有点, 若点满足且,则称点为中心点,点是点的 “界环绕点”.例如:对于中心点,满足且的点,都是点的“界环绕点”,这些环绕点组成的图形是一个边长为的正方形,中心点是正方形的中心.
(1)点的“界环绕点”所组成的图形面积为 ;
(2)直线经过点.
①在其图象上,点的“界环绕点”组成的线段长为,求b的值;
②直线与反比例函数图象的交点横坐标为,求的取值范围;
(3)关于的二次函数(是常数),将它的图象绕原点逆时针旋转得曲线,若与上都存在的“1界环绕点”,直接写出的取值范围.
五、综合题
18.
(1)计算:
(2)先化简,再求值: ,其中
19.
(1)已知A=2x2﹣x+y﹣4xy,B=x2﹣2x﹣y﹣xy+3,若(x+y﹣2)2+|xy+1|=0,求3A﹣2(A+B)的值.
(2)已知c<0<a,ab<0,|c|>|a|>|b|,化简:|b|﹣2|c﹣a|﹣|a+b|+|b﹣c|.
20.你能化简吗?我们不妨先从简单情况入手,发现规律,归纳结论.
(1)探究发现:先填空:
;
;
;…
由此猜想: .
(2)拓展应用:利用这个结论,你能解决下面两个问题吗?
①求的值;
②若,求等于多少?
六、实践探究题
21.
(1)【填空并观察猜想】①完成填空: ; ; (填“>”、“<”或“=”);
观察猜想:通过上面三个计算,可以初步对任意的非负实数,做出猜想:
②
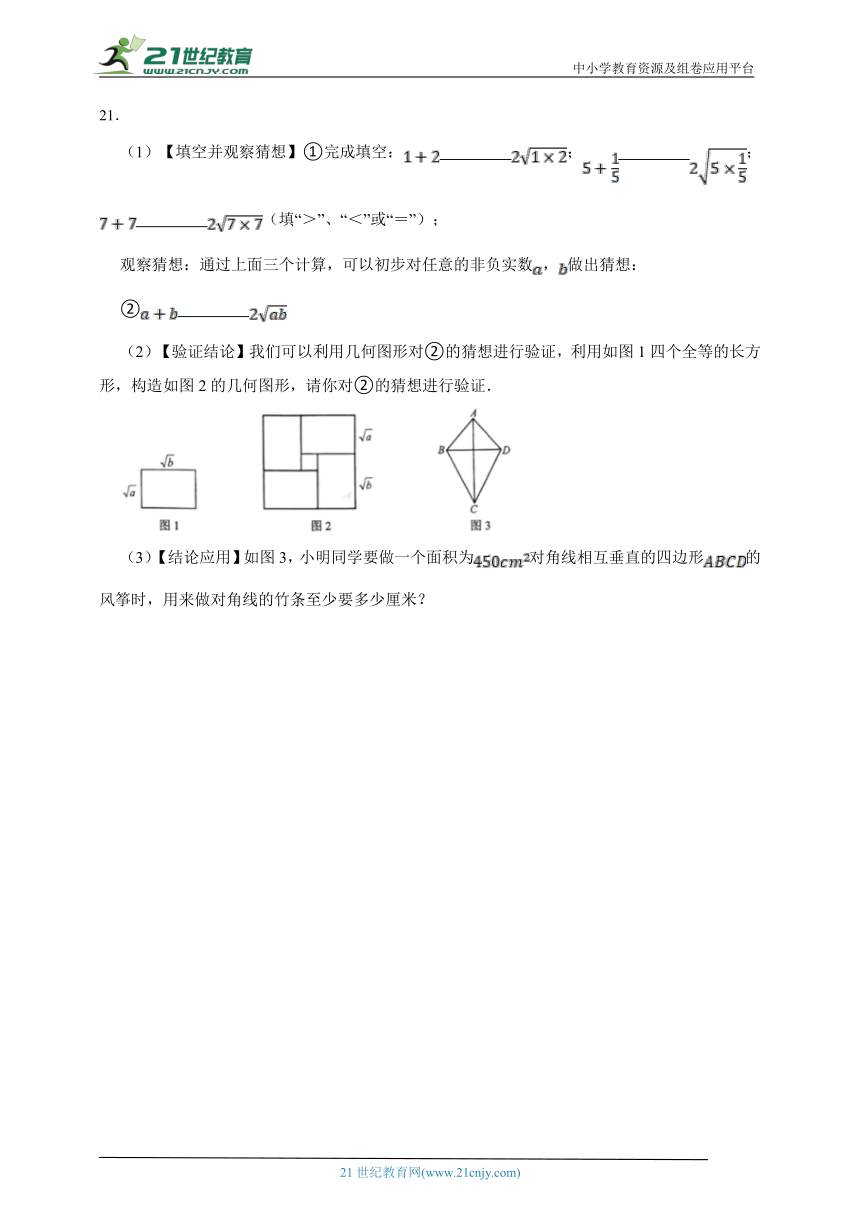
(2)【验证结论】我们可以利用几何图形对②的猜想进行验证,利用如图1四个全等的长方形,构造如图2的几何图形,请你对②的猜想进行验证.
(3)【结论应用】如图3,小明同学要做一个面积为对角线相互垂直的四边形的风筝时,用来做对角线的竹条至少要多少厘米?
答案解析部分
1.【答案】B
【知识点】整式的加减运算;同底数幂的除法;单项式乘单项式;幂的乘方运算
2.【答案】A
【知识点】同类项的概念
3.【答案】B
【知识点】合并同类项法则及应用
4.【答案】A
【知识点】整式的加减运算;多项式乘多项式
5.【答案】D
【知识点】二次根式的混合运算;定义新运算
6.【答案】1
【知识点】同类项的概念
7.【答案】3
【知识点】单项式的概念
8.【答案】25
【知识点】同类项的概念;合并同类项法则及应用
9.【答案】
【知识点】等边三角形的性质;勾股定理;探索数与式的规律;探索图形规律;坐标与图形变化﹣中心对称
10.【答案】406
【知识点】探索数与式的规律
11.【答案】②④
【知识点】解含绝对值符号的一元一次方程;绝对值的非负性;定义新运算;实数的绝对值
12.【答案】(1)解:原式=
=
=;
(2)解:原式=
=.
【知识点】有理数的加、减混合运算;合并同类项法则及应用
13.【答案】(1)解:(-3)2=(-3)×(-3)=9.
(2)解:1.53=1.5×1.5×1.5=3.375.
(3)解:
=×××
=
(4)解:原式=(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)=-1.
【知识点】有理数的乘方法则
14.【答案】解:原式=(1-2)(m-2n)2+(1-5)(m+n)=-(m-2n)2-4(m+n)∵-xm-2nym+n与-3x5y6是同类项,∴m-2n=5,m+n=6,∴-(m-2n)2-4(m+n)=-52-4×6=-25-24=-49.
【知识点】代数式求值;同类项的概念;合并同类项法则及应用
15.【答案】(1)解: 2a2b与2ab2不是同类项,
∵虽然它们所含字母相同,但相同字母的指数不相同,
∴2a2b与2ab2不是同类项;
(2)解: 3xy与yx 是同类项,
∵它们所含字母相同,且相同字母的指数也相同,
∴ 3xy与yx是同类项;
(3)解: -2.1与是同类项,
∵几个常数项是同类项,
∴ -2.1与是同类项;
(4)解: 2a与2ab不是同类项,
∵它们所含字母不相同,
∴2a与2ab不是同类项.
【知识点】同类项的概念
16.【答案】(1);;
(2)减少
(3)解:,
,
,
,
,
第二种方案变化后的面积比较大
【知识点】整式的加减运算;用代数式表示几何图形的数量关系
17.【答案】(1)4
(2)解:①设点的“界环绕点”为,
,,
①当直线与左边界相交时,与y轴交于点
∵,,
∴,
解得,,
∴直线不可能和下边界相交组成的线段长为.
②当直线与上边界相交时,
∵点,点,
∴,
∵,
∴,
∵,
∴,
∵,,
∴,
∴,即,
∴.
综上b的值为或或.
②把代入得:,
∴,
∴,
令,即,
由题可得:,,
∴
∵,
∴当,即时,有最小值,最小值为;
∴.
(3)解:
【知识点】一元二次方程的根与系数的关系(韦达定理);勾股定理;一次函数的性质;定义新运算
18.【答案】(1)解:
(2)解:
,
当 时,原式
【知识点】代数式求值;整式的混合运算;去括号法则及应用;完全平方式;实数的绝对值;分数指数幂
19.【答案】(1)解:2
(2)解:﹣b﹣3a+c
【知识点】有理数的减法法则;偶次方的非负性;绝对值的非负性;利用整式的加减运算化简求值;有理数的加法法则
20.【答案】(1);;;
(2)解:①,
由于,
∴;
②∵
∴
∴,
∴.
【知识点】探索数与式的规律
21.【答案】(1)>;>;=;≥
(2)解:图2中的中间小正方形的边长为,则其面积得
;
(3)解:设,
四边形对角线相互垂直
四边形的面积为
(厘米).
故至少要60厘米.
【知识点】完全平方公式及运用;探索数与式的规律
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
【沪科版七上同步练习】
第二章整式加减(能力提升)检测题
一、单选题
1.下列计算正确的是( )
A.3a+2b=5ab B.3a 2a=6a2
C.(2m2)3=6m5 D.a6÷a2=a3
2.若与是同类项,则等于( )
A. B. C. D.
3.下列单项式中,能够与合并的是( )
A. B. C. D.
4.设,,则M与N的大小关系为( )
A. B. C. D.不能确定
5.对于任意的正数a,b,定义运算★,,计算的结果为( )
A. B. C.2 D.
二、填空题
6.若代数式3a4b 与0.2b a4和仍然是单项式,则x的值是 .
7.在式子中,单项式有 个.
8.若单项式与单项式的和仍是一个单项式,则的值是 .
9.在如图所示的平面直角坐标系中,是边长为的等边三角形,作与关于点成中心对称,再作与关于点成中心对称,…,如此作下去,则的顶点的坐标是 .
10.在草稿纸上计算:① ;② ;③ ;④ ,观察你计算的结果,用你发现的规律直接写出下面式子的值 = .
11.规定:,,例如,,下列结论中,正确的是 (填写序号)
①若,则; ②若,则;
③能使成立的x的值不存在;④式子的最小值是5.
三、计算题
12.
(1)计算:
(2)化简:
13.计算:
(1)(-3)2.
(2)1.53.
(3)
(4)(-1)11.
14.已知-xm-2nym+n与-3x5y6的和是单项式,求 -5 -2 +(m+n)的值.
四、解答题
15.下列各组中的两项是不是同类项?为什么?
(1)2a2b与2ab2.
(2)3xy与yx.
(3)-2.1与
(4)2a与2ab.
16.如图,一块原边长分别为,的矩形,现将原矩形一边增加,另一边减少,变化后的面积为或.
(1) ; ; ;用含,的式子表示
(2)当时,变化后的面积会 ;增加或减少
(3)当时,有两种方案,第一种方案如图,第二种方案如图请你比较这两种方案,确定哪一种方案变化后的面积比较大.
17.定义:平面直角坐标系中有点, 若点满足且,则称点为中心点,点是点的 “界环绕点”.例如:对于中心点,满足且的点,都是点的“界环绕点”,这些环绕点组成的图形是一个边长为的正方形,中心点是正方形的中心.
(1)点的“界环绕点”所组成的图形面积为 ;
(2)直线经过点.
①在其图象上,点的“界环绕点”组成的线段长为,求b的值;
②直线与反比例函数图象的交点横坐标为,求的取值范围;
(3)关于的二次函数(是常数),将它的图象绕原点逆时针旋转得曲线,若与上都存在的“1界环绕点”,直接写出的取值范围.
五、综合题
18.
(1)计算:
(2)先化简,再求值: ,其中
19.
(1)已知A=2x2﹣x+y﹣4xy,B=x2﹣2x﹣y﹣xy+3,若(x+y﹣2)2+|xy+1|=0,求3A﹣2(A+B)的值.
(2)已知c<0<a,ab<0,|c|>|a|>|b|,化简:|b|﹣2|c﹣a|﹣|a+b|+|b﹣c|.
20.你能化简吗?我们不妨先从简单情况入手,发现规律,归纳结论.
(1)探究发现:先填空:
;
;
;…
由此猜想: .
(2)拓展应用:利用这个结论,你能解决下面两个问题吗?
①求的值;
②若,求等于多少?
六、实践探究题
21.
(1)【填空并观察猜想】①完成填空: ; ; (填“>”、“<”或“=”);
观察猜想:通过上面三个计算,可以初步对任意的非负实数,做出猜想:
②
(2)【验证结论】我们可以利用几何图形对②的猜想进行验证,利用如图1四个全等的长方形,构造如图2的几何图形,请你对②的猜想进行验证.
(3)【结论应用】如图3,小明同学要做一个面积为对角线相互垂直的四边形的风筝时,用来做对角线的竹条至少要多少厘米?
答案解析部分
1.【答案】B
【知识点】整式的加减运算;同底数幂的除法;单项式乘单项式;幂的乘方运算
2.【答案】A
【知识点】同类项的概念
3.【答案】B
【知识点】合并同类项法则及应用
4.【答案】A
【知识点】整式的加减运算;多项式乘多项式
5.【答案】D
【知识点】二次根式的混合运算;定义新运算
6.【答案】1
【知识点】同类项的概念
7.【答案】3
【知识点】单项式的概念
8.【答案】25
【知识点】同类项的概念;合并同类项法则及应用
9.【答案】
【知识点】等边三角形的性质;勾股定理;探索数与式的规律;探索图形规律;坐标与图形变化﹣中心对称
10.【答案】406
【知识点】探索数与式的规律
11.【答案】②④
【知识点】解含绝对值符号的一元一次方程;绝对值的非负性;定义新运算;实数的绝对值
12.【答案】(1)解:原式=
=
=;
(2)解:原式=
=.
【知识点】有理数的加、减混合运算;合并同类项法则及应用
13.【答案】(1)解:(-3)2=(-3)×(-3)=9.
(2)解:1.53=1.5×1.5×1.5=3.375.
(3)解:
=×××
=
(4)解:原式=(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)×(-1)=-1.
【知识点】有理数的乘方法则
14.【答案】解:原式=(1-2)(m-2n)2+(1-5)(m+n)=-(m-2n)2-4(m+n)∵-xm-2nym+n与-3x5y6是同类项,∴m-2n=5,m+n=6,∴-(m-2n)2-4(m+n)=-52-4×6=-25-24=-49.
【知识点】代数式求值;同类项的概念;合并同类项法则及应用
15.【答案】(1)解: 2a2b与2ab2不是同类项,
∵虽然它们所含字母相同,但相同字母的指数不相同,
∴2a2b与2ab2不是同类项;
(2)解: 3xy与yx 是同类项,
∵它们所含字母相同,且相同字母的指数也相同,
∴ 3xy与yx是同类项;
(3)解: -2.1与是同类项,
∵几个常数项是同类项,
∴ -2.1与是同类项;
(4)解: 2a与2ab不是同类项,
∵它们所含字母不相同,
∴2a与2ab不是同类项.
【知识点】同类项的概念
16.【答案】(1);;
(2)减少
(3)解:,
,
,
,
,
第二种方案变化后的面积比较大
【知识点】整式的加减运算;用代数式表示几何图形的数量关系
17.【答案】(1)4
(2)解:①设点的“界环绕点”为,
,,
①当直线与左边界相交时,与y轴交于点
∵,,
∴,
解得,,
∴直线不可能和下边界相交组成的线段长为.
②当直线与上边界相交时,
∵点,点,
∴,
∵,
∴,
∵,
∴,
∵,,
∴,
∴,即,
∴.
综上b的值为或或.
②把代入得:,
∴,
∴,
令,即,
由题可得:,,
∴
∵,
∴当,即时,有最小值,最小值为;
∴.
(3)解:
【知识点】一元二次方程的根与系数的关系(韦达定理);勾股定理;一次函数的性质;定义新运算
18.【答案】(1)解:
(2)解:
,
当 时,原式
【知识点】代数式求值;整式的混合运算;去括号法则及应用;完全平方式;实数的绝对值;分数指数幂
19.【答案】(1)解:2
(2)解:﹣b﹣3a+c
【知识点】有理数的减法法则;偶次方的非负性;绝对值的非负性;利用整式的加减运算化简求值;有理数的加法法则
20.【答案】(1);;;
(2)解:①,
由于,
∴;
②∵
∴
∴,
∴.
【知识点】探索数与式的规律
21.【答案】(1)>;>;=;≥
(2)解:图2中的中间小正方形的边长为,则其面积得
;
(3)解:设,
四边形对角线相互垂直
四边形的面积为
(厘米).
故至少要60厘米.
【知识点】完全平方公式及运用;探索数与式的规律
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
